数列中探索性问题的类型与破解策略

江苏省大丰高级中学 (224100) 姜兴荣

数列中的探索性问题是近年高考中比较常见的一类创新性问题，借助创新情境设置，结合条件探索、结论探索、存在探索等不同类型来合理设置，根据数列中的定义、通项公式、求和公式以及相关性质等加以变形与应用，合理变形，巧妙放缩，从条件出发，通过观察、试验、运算、归纳、类比、猜想来剖析与转化，大胆的猜想，总结规律，能较好达到创新能力培养的教学目标.

1.条件探索性问题

数列中条件探索性问题的基本特征是：针对一个确定的结论，条件未知需探求，或条件增删需确定，或条件正误需判定等.解决此类数列中条件探索性问题的基本策略是：执果索因，先寻找结论成立的必要条件，再通过检验或认证找到结论成立的充分条件.特别注意，在“执果索因”的过程中，常常会犯的一个错误就是没有充分考虑推理过程是否可逆，误将必要条件当作充分条件.

例1 已知函数f(x)=logkx(k为常数，k>0且k≠1).

(1)在下列条件中选择一个，使得数列{an}是等比数列，并说明理由；

①数列{f(an)}是首项为2，公比为2的等比数列；

②数列{f(an)}是首项为4，公差为2的等差数列；

③数列{f(an)}是首项为2，公差为2的等差数列的前n项和构成的数列.

分析：(1)根据等比数列的定义，结合不同条件建立对应的f(an)的关系式，通过数学运算与变形来分析；(2)结合(1)的结论与对应的条件，确定数列{bn}的通项公式，利用通项公式的裂项相消法进行数列求和.

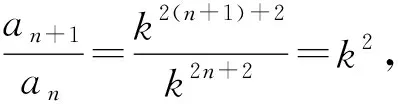
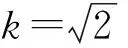
点评：涉及数列中的条件探索性问题，根据不同条件加以合理推理与转化，通过数列中定义、公式、性质等的应用来分析与运算.此类条件探索性类问题，可以通过数列中的不同条件来分析对应的结论，也可以通过数列中的确定结论来反推满足题意的条件等.

2.结论探索性问题

数列中结论探索性问题的基本特征是：有确定的条件，而无结论或结论的正确与否需要加以确定.解决此类数列中结论探索性问题的基本策略是：先探索结论而后去论证结论.在探索结论的过程中，常常可先从特殊情形入手，通过观察、分析、归纳、判断来作一番猜测，归纳出相应的结论，再就一般的情形加以论证即可.

例2 已知各项均不为零的数列{an}的前n项和为Sn，且满足a1=4，an+1=3Sn+4(n∈N*).

(1)求数列{an}的通项公式；

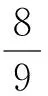
分析：(1)结合数列的递推关系式，合理变形，结合等比数列的定义确定数列类型，进而确定对应的通项公式；(2)通过(1)的结论以及条件中关系式确定bn的关系式，利用通项公式的错位相减法进行数列求和，借助不等式的放缩法来确定大小关系问题.

点评：涉及数列中的结论探索性问题，需要先得出一个结论，再进行证明.特别涉及数列中含有两个变量的问题，“变量归一”是常用的解题思想，一般把其中的一个变量转化为另一个变量，根据题目条件，确定变量的值.特别，当遇到数列中的比较大小问题时可以采用构造函数，根据函数的单调性进行证明，也可利用数列放缩加以变形转化，这都是解决这些相关问题中比较常用的方法.

3.存在探索性问题

数列中存在探索性问题的基本特征是：要判断在某些确定的条件下，某一数列对象(首项、项数、参数等)是否存在或某一结论是否成立.解决此类数列中存在探索性问题的基本策略是：假定题中的数列对象存在或结论成立，有时也可以暂且认可其中的一部分结论，然后在这个前提下进行逻辑推理，若由此导出矛盾，则否定假设；否则，给出肯定结论.在这个过程中，反证法在探索解题中起着至关重要的作用.

已知{an}是公差为2的等差数列，其前n项和为Sn，.

(1)求数列{an}的通项公式；

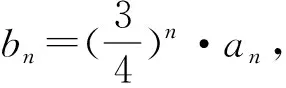
分析：(1)根据条件的选择，从不同角度，结合不同数列类型加以变形与转化，进而确定数列{an}的通项公式；(2)结合(1)的结论与对应的条件来确定bn的关系式，利用作差比较法进行合理变形，通过项数n的取值情况确定数列{bn}中的最大项，进而确定数列的存在性问题.

点评：遇到数列中的多个变量的存在性问题，一般先假设存在性成立，求出满足条件的关系，再进一步寻找满足的条件即可；而根据条件推出矛盾则说明不存在.破解此类问题一般可以利用数列的函数性质、重要不等式、函数的值域或取值范围等的判断来确定对应的存在性问题.

处理数列中的探索性问题，应充分利用已知条件或对应的结论，合理根据数列前几项的特点透彻分析、发现规律、猜想条件或结论或存在性等，经常综合不等式的性质(包括放缩法等)、函数的性质等加以合理运算与推理，从而得以解决探索性问题，提高数学应用能力与创新能力，综合数学知识、数学思想方法和数学能力的应用，养成良好的数学品质，培养数学核心素养.