不可轻用的位似形坐标规律

刘家良

位似形坐标规律揭示了位似形对应点坐标之间的联系，但需要注意的是：只有当位似中心为原点时，方能利用位似形坐标规律求位似形中相应点的坐标.

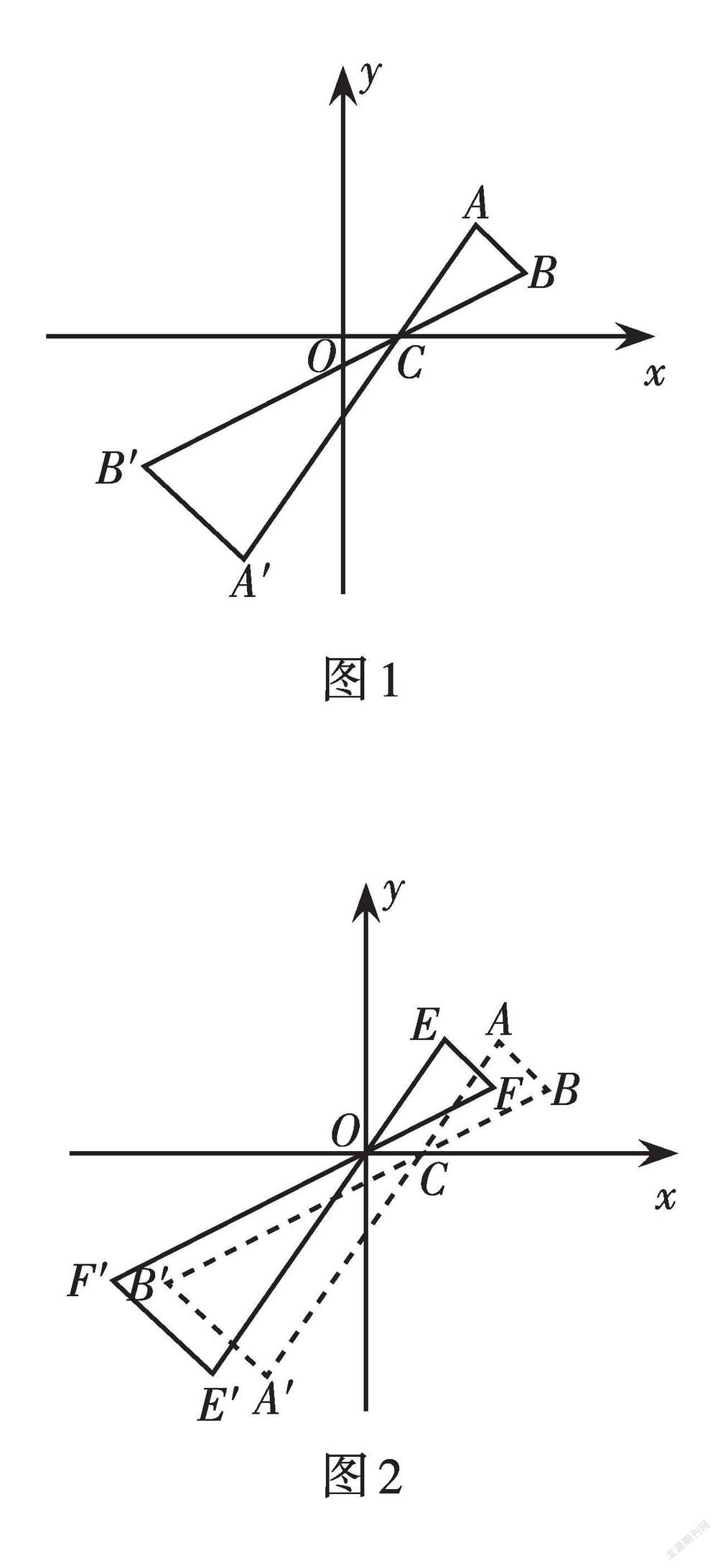
例 （2021·山东·东营）如图1，△ABC中，A，B两个顶点在x轴的上方，点C的坐标是（1，0），以点C为位似中心，在x轴的下方作△ABC的位似图形△A'B'C，并把△ABC的边长放大到原来的2倍，设点B的横坐标是a，则点B的对应点B′的横坐标是（ ）.

A.  -2a + 3 B.  -2a + 1

C.  -2a + 2 D.  -2a - 2

分析：位似中心为点C（1，0），不是原点，所以不能直接利用位似图形的坐标规律求B′的横坐标，须将位似中心C平移到原点处.

解：∵点C的坐标是（1，0），点O的坐标是（0，0），∴可将位似形沿CO方向平移1个单位长度，使位似形中心为原点，如图2，则点B平移后的对应点F 的横坐标为a - 1. ∵相似比k = 2，且位似形在位似中心O的两侧，∴点F′的横坐标为-2（a - 1）. 再将点F′向右平移1个单位长度，可得点B′的横坐标为-2（a - 1） + 1，即-2a + 3. 故选A.

注意：利用位似形坐标规律时，一看位似形是在原点的同侧还是两侧，同侧则乘k，两侧则乘-k（k为位似比）;二要看位似中心是否为原点，若不是原点，须先将原图形平移到原點处，再利用位似形坐标规律求出平移后点的坐标，注意求位似点的坐标时还要再平移回去（这一过程称为“两平移”）.

能力提升

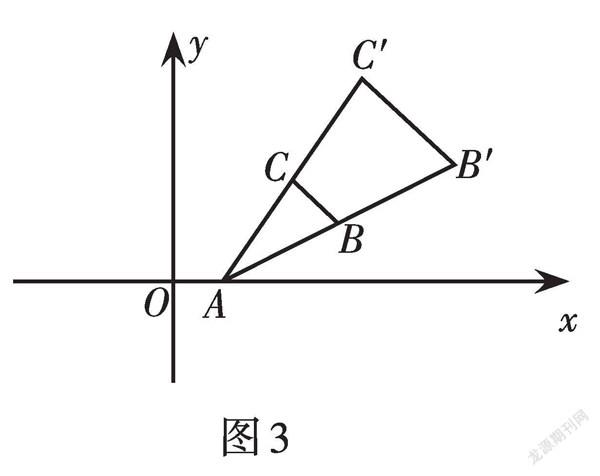
如图3，△ABC中，B，C两个顶点在x轴的上方，点A的坐标是（1，0），以点A为位似中心，在x轴的上方作△ABC的位似图形△AB'C'，并把△ABC的边长放大到原来的2倍，设点B的横坐标是a，则点B的对应点B′的横坐标是 .

答案：2a - 1.