潮流方程的割线法求解

赵 泽，何飞跃

（中国水利水电科学研究院 自动化研究所，北京 100038）

1 研究背景

潮流计算是指在电力系统中给定输入的有功功率和无功功率，线路参数以及网络结构，计算线路潮流分布以及节点电压的一类算法。潮流计算是电力系统分析中最重要、最基本的计算，是电力系统运行、规划及安全、可靠性分析和优化的基础。经典的牛顿类方法是电力系统潮流计算的应用方法之一，虽然具有二阶的收敛特性，但其对初值的敏感性较高。文献［1］通过缩小初值的选择范围来改善牛顿类潮流计算的收敛性。另外，先使用快速分解法［2-4］求得合理的迭代初值，然后使用牛顿法对潮流方程进行迭代求解，是连续潮流求解的常用方法。

割线法是一个传统的解偏微分方程的方法。本文将割线法应用于潮流计算中，通过对潮流方程的简化和计算修正，快速准确解出潮流方程。

2 割线法介绍

2.1 差商思想的割线法 一般的牛顿-拉夫逊法的表示为：

为了避免对每次迭代形成新的雅克比矩阵，通过差商的思想，将微分方程化为代数方程：

将式（2）带入式（1）即得到了割线法迭代方程：

图1和图2所示分别表示N-R法和一般型割线法。从图中可以看出，割线法需要两个初值才能进行迭代计算。图3为改进型的割线法，要求f（xk-1）⋅f（xk）＜0。

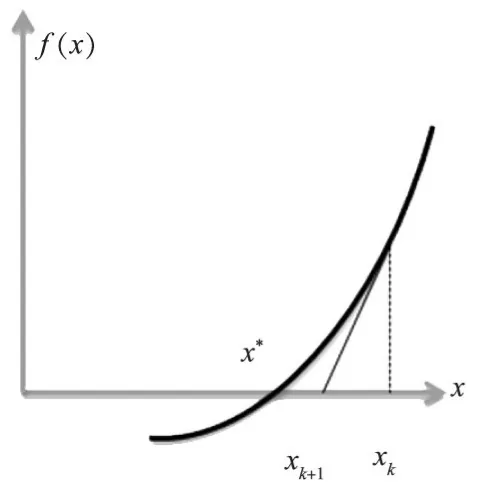
图1 N-R法

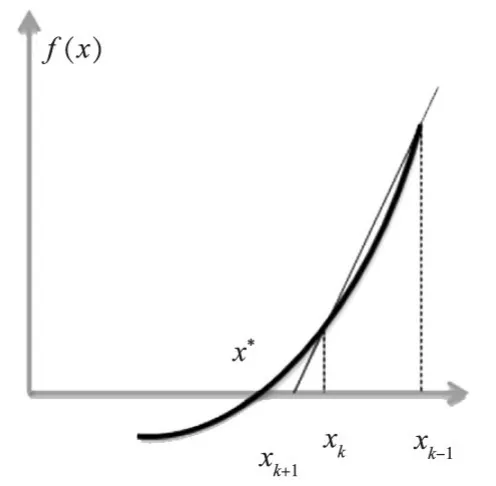
图2 一般型割线法

2.2 收敛性在文献［5］中指出，单根情况下N-R法具有二阶收敛性。在选取初值较好的情况下，N-R法可以很快迭代收敛到方程的解，但由于其每次迭代都要求取新的雅可比矩阵，一次计算速度大大下降，合适的初值并不容易估计到，所有单独的N-R法并不适合快速潮流的求解。快速分解法是一种定雅可比法，是对雅可比矩阵进行了简化，并且节点功率偏差量的计算及收敛条件都是严格的，因此能够保证计算结果的准确性；快速分解法仅有线性收敛速度，但是其鲁棒性较好，适合在线计算［6］。割线法的收敛阶为1.618［5］，理论上，在相同的迭代条件下，割线法迭代次数介于牛顿-拉夫逊法和快速分解法之间，具有快速迭代的特点。本文对割线法进行了改进和条件约束，有效保证了合适的迭代方向，而且经过后文的仿真验证，结果的准确性也能得到保障。

3 割线法潮流计算

3.1 潮流方程极坐标形式的潮流方程［6］：

式中：是给定量，是节点的注入功率；Gij和Bij是节点导纳矩阵的实部和虚部。

3.2 迭代初值设第k次迭代的结果为集合虽然割线法对初值的选择不敏感，但是多值迭代的情况下，可能会出现个别值的单次迭代精度差异较大，增加迭代的次数。因此，选择初值应符合电力系统需求。

3.3 迭代方程的简化及迭代方向的修正由于割线法求解潮流时需要两组迭代结果作为初值进行下一次迭代，如集合X（2）基于集合X（0）和集合X（1）获得。根据高斯-塞德尔迭代的思想，对潮流方程做类似的迭代处理，迭代出来的新值在随后的迭代中立即使用，见下式：

4 算法实现

改进的割线法［7］是利用根的存在定理，引导一个正确的迭代方向，见图3所示。

基于文献［7］对割线法的优化思想，实现了单一变量的割线法求解，每次迭代会修正迭代方向，改进了割线法的迭代速度。文献［7］提出的改进的割线法的思想，实现多变量的割线法求解。每次每个变量的迭代使用改进的割线法来保证每次迭代的正确方向，每次迭代每个变量之间借鉴高斯-塞德尔迭代的思想，修正变量的迭代值，使迭代结果向真实值靠拢。

4.1 割线法的优化由上述讨论，已经将潮流方程化成了多个单变量的代数方程的求解，设任意一个变量和任意一个潮流方程分别为x和f（x）。

文献［7］给出了单值求解的改进型迭代算法：

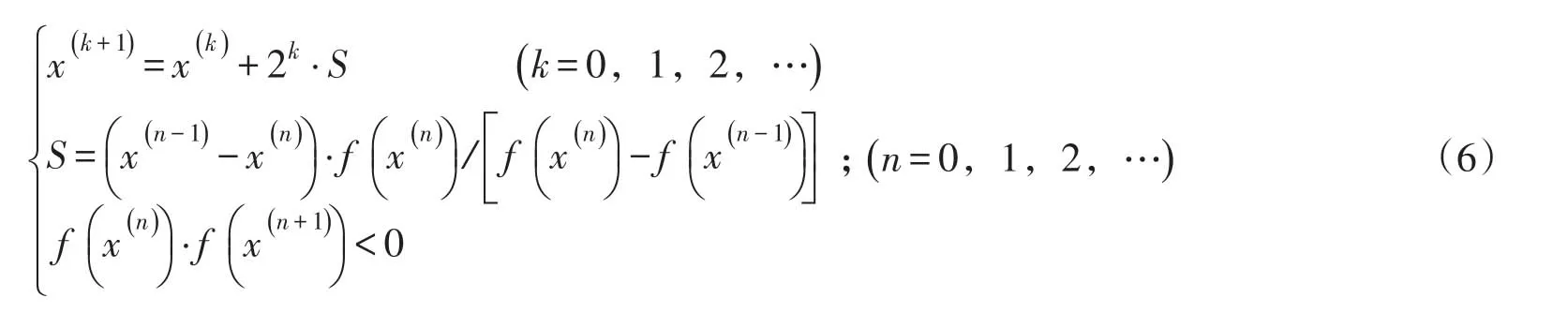
4.2 割线法的迭代过程综合割线法潮流计算分析和改进型迭代算法的实现，给出割线法潮流计算的迭代过程。

（1）给定初值x0，x1。如果转（2）；否则，令x1=x1+2kS，其中S=(x0-x1)⋅直至取到满足转（7）；否则转（4）。（4）执行k=k+1，x2=x1+2kS，直至转（5）。（5）如果转（6）。（6）x0=x1，x1=x2，x2=x1+S ，转（3）。（7）x0=x1，x1=x2；转（2）。

5 算例分析

图4和图5所示的三母线电力系统，已知t=1.05，PD1+jQD1=2+j1，PD2+jQD2=0.5+j0.25，PG2=1，V2=1.01，V3∠θ=1∠0°，用割线法计算极坐标形式的潮流方程。

节点①为PQ节点，节点②为PV节点，节点③为Vθ节点；待求参数为θ1、θ2、V1。

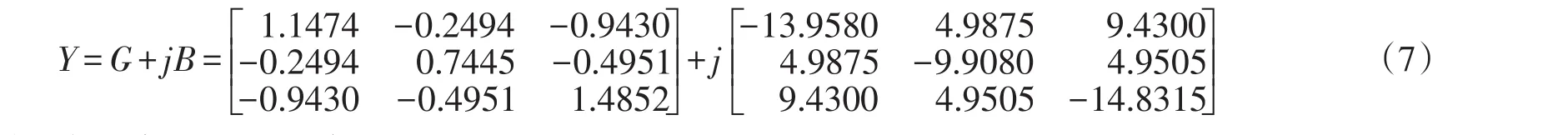
容易列出潮流方程，此处略去。

割线法的迭代方程：

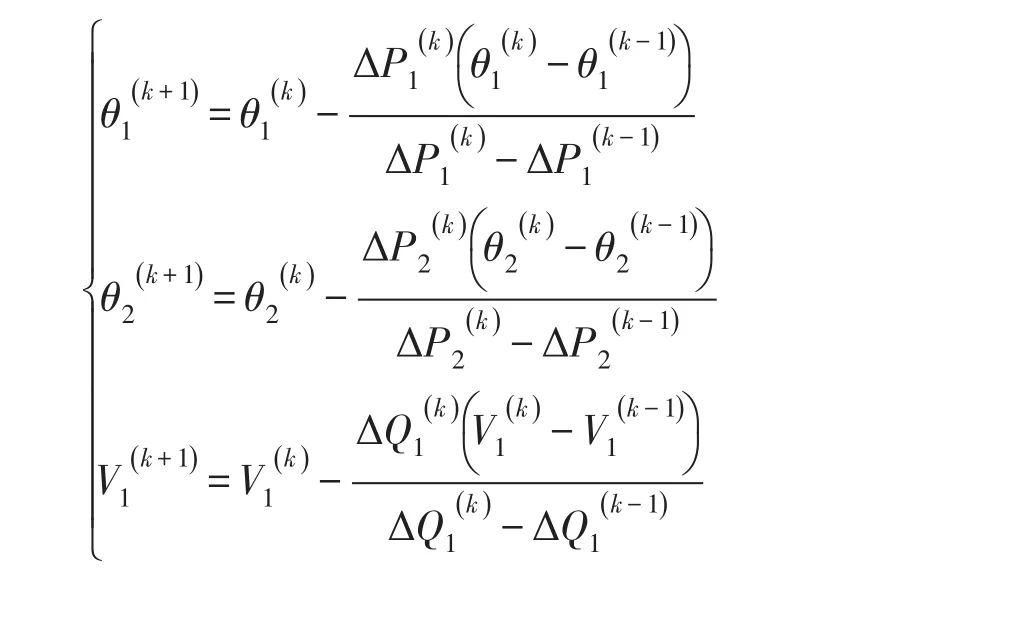
图4 三母线电力系统

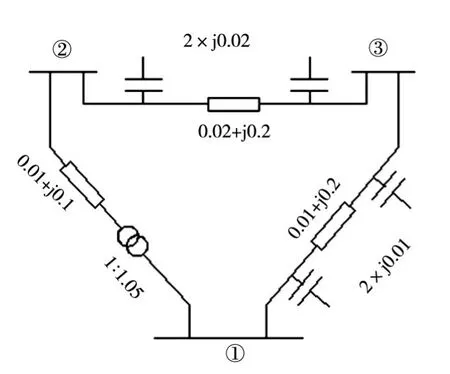
图5 节点编号后的三母线电力系统

需要6个初值才能进行迭代，

取初始值取初始值

利用割线法的迭代算法，收敛阀值为0.0000 5，求解结果列于表1中。运算时间0.0052 s。

表1 三母线系统割线法求解的迭代结果

利用快速分解法，使用平启动的方式进行潮流计算；计算结果见表2。运算时间0.0049 s。

利用N-R法，使用平启动的方式进行潮流计算；计算结果见表3。运算时间0.026 s。

表2 三母线系统快速分解法求解的迭代结果（平启动）

表3 三母线系统N-R法求解的迭代结果（平启动）

根据经验，电压一般都是在标幺值1.0附近，所以选择初值时电压的取值应在1.0左右；而相角的变化不易确定，但是一般节点间的角度差不会太大。经过测试，改进型割线法经过5-8次迭代后收敛到5×10-5，其迭代结果与快速分解法和N-R法吻合，保证了用割线法求解的正确性。计算时间与快速分解法近似，效率上优于N-R法。由于N-R法每次迭代重新生成雅可比矩阵，导致单次迭代计算时间较长，所以，虽然迭代次数少，但是总的计算时间较长。

图6和图7反应了初值选择对N-R法和割线法计算效率的影响，可以观察到θ1从-1到1变化，初值选择在真实值附近时，迭代次数较少，计算时间较短。当初值选择为0.8后，N-R法的迭代此时达到了16次，计算时间达到了0.156 s；而割线法的迭代次数维持在6-8次，计算时间为0.005-0.007 s。割线法在保证计算时间的同时，可以有效避开初值的选择对迭代收敛性的影响。

图6 N-R法迭代次数和迭代时间趋势

图7 割线法迭代次数和迭代时间趋势

6 结论

本文讨论了割线法在求解潮流方程的有效应用，并用改进的割线法和简化的潮流方程给潮流方程的求解提供了新的思路。割线法求解潮流方程可以避开初值对迭代过程收敛性的影响，并使迭代过程向着真实值的方向发展，可以有效的提高计算的速度。本文中实现了对潮流方程的变量的简化、迭代方向的修正以及迭代过程的改进，验证了割线法求解潮流方程的可行性、准确性和时效性，有利于快速准确地求解潮流分布。

参考文献：

［1］孙秋野，陈会敏，杨家农，等.牛顿类潮流计算的收敛性分析［J］.中国电机工程学报，2014，34（13）：2196-2200.

［2］STOTT B，ALSAC O.Fast decoupled load flow［J］.IEEE Trans.PAS，1974，93（3）：859-869.

［3］MONTICELLI A，GARCIA A，SAAVEDRA O R.Fast decoupled load flow：hypothesis，derivations and testing［J］.IEEE Trans.on Power Systems，1990，5（4）：1425-1431.

［4］AMERONGEN R V.A general-purpose version of the fast decoupled load flow［J］.IEEE Trans.on Power Sys⁃tems，1989，4（2）：760-770.

［5］关治，陆金甫.数值分析基础（第2版）［M］.北京：高等教育出版社，1998.

［6］张伯明，陈寿孙，严正.高等电力网络分析（第2版）［M］.北京：清华大学出版社，2007.

［7］徐裕生，刘勇，冯春强.一种改进的割线法［J］.纺织高校基础科学学报，2006，19（1）：36-38.