基于学习路径分析的“角的度量”单元整体教学*——以认知阶段建构度量教学

□邵蓓瑜 章勤琼 麻永侃

《义务教育数学课程标准（2022年版）》指出：“量感主要是指对事物的可测量属性及大小关系的直观感知。知道度量的意义，能够理解统一度量单位的必要性。”［1］这说明对角的度量，首先需要让学生直观感知角有大小，知道角具备可测量属性，其次才能进行角的比较，并在描述角的大小过程中产生统一单位的需求。但在实际学习中，学生往往还不知道“角的大小”，就已经开始学习运用量角器量角、画角的技能。在“角的度量”单元中，设计怎样的学习任务才能帮助学生理解角有大小，在度量的过程中理解度量的本质呢？因此，本文从度量教学的认知顺序出发，根据学习路径，对这一单元做了整体教学的思考。

一、确定学习目标

（一）单元内容概述

人教版教材关于“角的度量”单元的教学目标如下：（1）认识角的静态概念，即从一点引发的两条射线所组成的图形；（2）角的度量，通过间接比较来认识角的度量单位和用量角器量角的度数；（3）角的分类，认识角的动态概念，进一步认识直角、锐角，知道平角和周角，并了解这几种角的大小关系；（4）画角，会画特定度数的角。

北师大版教材关于“角的度量”单元的教学目标如下：（1）动态再认识角，结合旋转的操作活动认识平角和周角，了解周角、平角、钝角、直角、锐角之间的大小关系，发展推理能力；（2）探索角的度量单位的产生过程，认识角的度量单位；（3）会用量角器等工具量角和画角。

对比两个版本的教学目标，可以看到该单元中角的度量部分都包含3个方面：（1）角的内涵，只是人教版从静态概念（从一点引发的两条射线所组成的图形）中理解，北师大版从动态角（旋转活动角）中理解；（2）在间接比较中认识角的度量单位；（3）会用量角工具量角和画角。

（二）单元核心目标

刘加霞教授指出：“生活中有6种常用的感官量：长度、质量、容积、角度、面积、体积。”学生对于它们的学习以及理解，通常会经历以下5个阶段：阶段1，量的初步认识；阶段2，量的间接比较；阶段3，认识国际通用单位并能够用其描述大小；阶段4，国际通用单位体系的认识与换算；阶段5，利用公式求量的大小。［2］根据度量教学的一致性可知，角的度量包括以下3个阶段：角的认识；比较角的大小；认识角的单位1°并能够用单位1°描述角的大小。

由此可知，“角的度量”这一单元的核心目标为：（1）角的内涵，指的是学生能够直观知道角有大小，直接和间接比较角的大小。（2）在描述角的大小中产生度量单位。因此，“角的度量”单元的核心目标分为两个方面：角的大小比较中理解角的内涵和描述角的大小中产生度量单位。［3］

（三）核心目标具体化

1.角的大小比较中理解角的内涵

角的度量首先要让学生知道角有大小，然而角的大小非常抽象。理解角的内涵有三个层次：（1）直观感知角有大小，比如活动角开口变大，就是角变大了。（2）直接比较角的大小，比如借助移动重合（让顶点对顶点，边对边，看另一边）比较角的大小。（3）间接比较，选择一个合适的小角作为工具来度量。

2.描述角的大小中产生度量单位

要具体描述一个角的大小或两个角相差多少，都需要寻找一个合适的小角作为工具来度量，看目标角中包含了多少个小角，通过“数+单位”来描述角的大小。因此，描述角的大小认知有两个阶段：（1）用非标准角描述；（2）用标准1°描述。

二、确定学习起点

为了解学生的学习起点，借鉴范希尔几何水平理论，以角的概念、直接比较、间接比较来评估学生对角的内涵的理解水平（如表1），对四年级1个班42名学生进行前测。

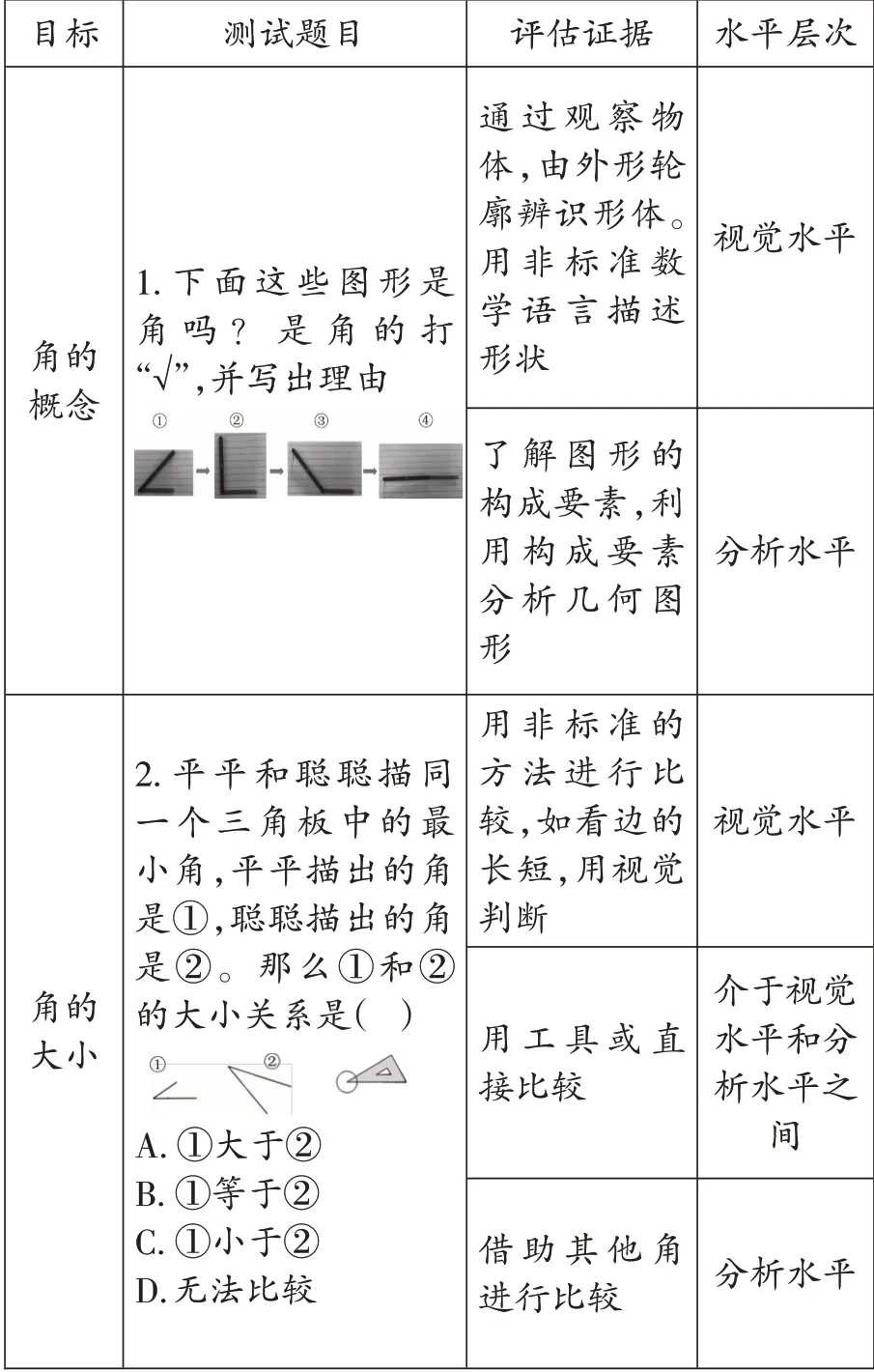
表1 “角的度量”单元核心目标的表现性评价框架

（一）角的概念理解情况

在测试题1的访谈中发现，有79%的学生属于视觉水平。他们用图形的整体轮廓“角是尖的、斜的，用锐角、直角、钝角的样子”作为依据判断角。有12%的学生介于视觉水平和分析水平之间，此类学生虽然能用角的构成要素——一个顶点和两条边来判断①～③号图形，但还是会受到视觉影响而无法判断④号图形。仅9%的学生达到分析水平，能用角的构成要素——一个顶点两条边来进行判断。因此，要达到用角的概念来判断角的目标，首先要让学生理解角的内涵。

（二）角的大小理解情况

角的内涵测试题2中，有32.6%的学生处于视觉水平，能剥离画的边的长短和朝向等无关因素的学生占全班的67.4%（如表2）。通过访谈发现，这67.4%的学生中，有15.2%的学生是用量角器进行测量的，有8.7%的学生是通过眼睛看出来的，这些学生通过视觉来直接比较出结果。有26.1%的学生用三角尺中的最小角作为单位来间接比较出结果，有17.4%的学生能直接根据题目中的小角描同一个角，这些学生能真正突破画的边的长短和方向带来的干扰。由此可知，全班只有43.5%的学生具有间接比较的经验，56.5%的学生需要补充角的大小比较的经验。

表2 学生角的大小理解情况

通过对学生角的内涵理解水平的前测，从“角的概念”测查中发现约79%的学生不会用构成要素分析角，从“角的大小”测查中发现约57%的学生缺乏间接比较的经验。因此，本单元教学需要重视对角的内涵的学习，增加比较角的大小的练习。

三、分析学习路径

基于以上分析，对“角的度量”单元的学习路径做了相应的调整与优化。

首先，理解线段、射线与直线等角的构成要素的合理性。借助画图体会概念构成要素“端点、无限长”表达的合理性。重点是对无限长与端点逻辑关系的理解。

其次，增加理解角的内涵的内容。原因有以下三点：（1）根据学情测查，约57%的学生缺乏间接比较经验。仅靠人教版教材例2“从一点出发的两条射线所组成的图形叫作角”的静态含义，学生并没有积累例3角的度量中所需要的间接比较经验。（2）学生需要通过“点对点、边对边、看另一边”的直接比较方法感知等价角含义，理解角的内涵，消除画的边的长短带来的迷惑。（3）学习例2的静态角概念，也无法帮助学生理解例3中“一个圆平均分成360份，其中的1份是1°”的规定是合理的。因此，《角》一课要达成以下三点目标：（1）通过旋转活动角，让学生直观感知角的大小。（2）通过对角的直接比较，建立角的大小比较方法和使用等价角的概念，体会角的构成要素是射线的合理性。（3）通过间接比较角的大小，增加活动经验和概念理解。

再次，经历角的度量单位的形成过程。（1）在无法直接比较时，需要选择合适的小角作为一种工具来度量角的大小，并用“数+小角”的形式描述角的大小。让学生经历完整的用非标准单位（小角）描述角的大小的过程，渗透度量意识才是有效的。（2）对小角量化结果10°的理解，从10°角的累加或细分中描述不同角的大小。建立角的度量单位1°。（3）用1°的角量角的大小，体会度量的本质。

最后，通过量角器量角和画角。

四、单元整体教学思考及核心课时任务设计

综上所述，增加了“角的再认识”和“认识角的度量单位”两个内容，更符合度量认知的顺序和学生的认知规律。单元教学具体安排如表3。

表3 “角的度量”单元教学安排

从单元整体的视角出发，关于角的度量部分有两节核心课：“角的再认识”和“认识角的度量单位”。现对这两个内容的学习目标和学习任务设计如下（见表4）。

表4 “角的度量”单元优化后核心课时学习目标和学习任务