立足“建模”讲好“故事”——以“折线统计图”为例谈模型思想教学

□许贻亮

模型思想是数学基本思想之一。在《义务教育数学课程标准（2022年版）》中，模型思想的上位表达是“数学语言”，即“会用数学的语言表达现实世界”。模型思想教学是一个“综合”的感悟过程，并不仅仅体现于“问题情境—建立模型—求解验证”的数学活动过程，而应考虑核心素养的整体性、一致性。在小学阶段，与模型思想对应的核心素养主要表现为模型意识、数据意识和应用意识。数学教学中应全程、全局地给予关注与把握。史宁中教授提出“模型思想就是用数学的语言讲述现实世界的故事”。因此要把模型思想真正落实，需要从数学与现实世界两个角度入手讲好“故事”。如果把模型思想教学比作一首交响乐曲的演奏，就需充分考量音准、旋律、回声。以“折线统计图”教学内容为例，从折线统计图的“形、质、神”三个视角阐述模型思想教学。

一、观其形：调好“故事”的音准，发展模型意识

数学教学内容中有着大量的模型，包括各种用字母、数字及其他数学符号建立起来的代数式、关系式，以及各种图表、图形等。“问题情境—建立模型—求解验证”是数学建模的主要过程，其中建构模型是“核心”。而在建构模型的过程中，需要关注原型的撷取与改造，以原型的特殊感受模型的一般，以原型的直观把握模型的抽象，从而达成“对数学模型普适性的初步感悟”。以“折线统计图”为例，学生已经从电视、手机、报刊、家长理财投资等信息中，获取了一定的“前经验”，这是教学素材的资源库，我们可从中撷取适切的原型，为模型意识的建立定好基调。

在“折线统计图”教学中，教师以运动腕表“一周的步数情况”（简化版的折线统计图，如图1）导入。教师先让学生借助生活经验进行观察、分析、交流，然后提问：“这幅图告诉你怎样的‘故事’。”学生从整体上感知折线统计图变化趋势中的3个特征“升、平、降”，并直观地判断出哪天步数最多、哪天步数最少。教师再追问：“课件中没有声音，是谁告诉你这个‘故事’的？”透过生活原型的直观表象，学感悟到折线统计图的两个核心要素：点和线。由此，学生感受到数学语言的简洁美，为折线统计图这一数学模型调好音准。

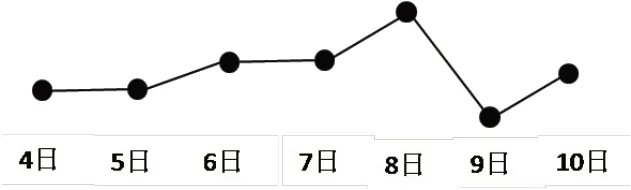
图1

在此基础上，教师以现代科技产品为主线，串联起心率腕表中简化版心电图像、智能音箱2015～2020年的销售情况等，使折线统计图的特征和数学语言表达的特点、要素等在同一主题情境中的变化得以联系、深化。在这个过程中，学生经历、体验两个层次的“故事”讲述。第一层次，用一个“点”讲故事。如2017年销售800台，“点”在哪里？教师以“陌生情境”促使学生联系原有知识经验中的“数对”与“条形统计图”，关注折线统计图中的横轴与竖轴两个维度，找到横轴“年份上的2017”与竖轴“数量上的800”的交点，从而完成第一次用“点”的数学表达，再举一反三，如2015年销售300台，体会“点”的价值，即表达数量的多少。第二层次，用一条“线”讲故事。在表达“2016年比2015年有一定的提高”时，学生在3条上升趋势不同、长短不同的线段中做具体选择，感受同一种线段包含着丰富的数学语言内涵（销量只上升了一点点、销量有一定地上升、销量大大地上升）。在迁移到其他年份销售量的表达的过程中，学生感悟到不同年份间线段越长、坡度越大则表示变化趋势越明显，体会到“线”的价值，即表达变化的趋势。最后，学生在与统计表的对比和转化中，完成折线统计图的绘制，并梳理出绘制要点：描点、标数、连线，从而实现折线统计图数学模型的整体建构。

建立模型意识常有两种不同的路径，一是从现实问题或生活原型入手，二是从原有知识迁移入手，教师可以依据教学目标灵活选择。同时，要把握好它与抽象、推理的关系，要认识到感悟过程中的“思想基础是抽象与推理”，在建构模型的经历中“有意识地用数学的概念与方法予以解释”，让学生获得对数学本质的理解。

二、品其质：弹好“故事”的旋律，发展数据意识

在“描述与交流现实世界的表达方式”中，数据占有重要的地位。数学教学要使学生“能够理解数据的意义与价值，会用数学的分析结果解释和预测不确定现象，形成合理的判断或决策”。因此在模型思想的教学中，要始终关注数据意识的感悟，使学生对数据有更为理性的认识，能够理解确定数据背景下随机结果的合理性与或然性。以折线统计图为例，教师在带领学生收集、整理、分析数据后，要重点关注学生对数据发展趋势如何进行判断与预测，使他们做出合理的决策。

在“折线统计图”教学中，教师让学生扮演“投资人”的角色，以“投不投”为核心问题，引导学生根据智能音箱专卖店2015～2018年的销售情况进行数据分析并做出自己的判断，使学生作为主角“投资人”参与“故事”中，进一步丰富对数据的感悟（如图2）。

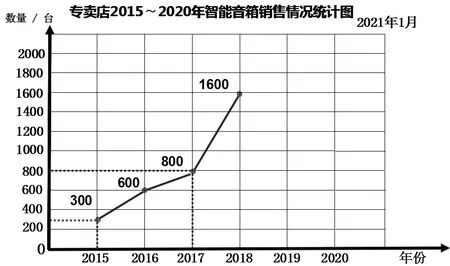
图2

投资故事1：2019年投不投？多数学生受到2015～2018年都是呈上升趋势的影响，选择“投”，体现了对变化趋势整体性的心理认知趋同。也有部分学生从2017～2018年销量大幅度上升的数据变化中产生顾虑“上升太快，还会再上升吗”，采取谨慎的态度“不投”。此时，学生所做出的判断多是凭借生活经验，更像是一种对数据的直觉。教师在课件中出示2019年实际销售量为1800台，由实际销量对学生做出的数据判断进行回应，以此强化学生对数据变化的感悟，激发学生的好奇心和求知欲，让学生做“有眼光的投资人”。

投资故事2：2020年投不投？这时，有了“投资故事1”的经历，更多学生从“对数据的直觉”转向“对数据的分析”，投资判断倾向于“用数据说话”。如2018～2019年只增长200台，比2017～2018年增长的800台少太多了，不投；增长的速度变慢，有可能市场快要饱和了，不投。在课件出示2020年实际销售量只有1300台时，让学生思考“销量大幅度下降的原因”“2020年有什么故事”等问题。学生从“对数据的具体数值”到“对数据的现实背景”思考，理解了2020年疫情对智能音箱专卖店销量的影响，感悟到生活事件中蕴含的随机性，增强了数据判断的理性因子。面对2019年的“升”和2020年的“降”，那么“2021年投不投”。学生从“今天”展望“未来”，再次进行独立思考、交流表达，使判断与决策更有数学味。

对于数据的判断与决策，我们应坚持“合理”的原则，即不要求答案的统一或唯一，而要关注学生做出判断与决策时理由的合理性，言之有理、言之有据都是可以的。正如陈希孺教授所强调的：“统计没有对错之分，只有好坏之分。”只有坚持“合理”的原则，弹好数据意识感悟的主旋律，才能让学生对数据分析与判断具有敏感性。教学中，有意识地把对统计思想与随机思想的感悟融合，发展学生的数据决策力和学习自信心，可以为感悟模型思想积累活动经验。

三、悟其神：响好“故事”的回声，发展应用意识

史宁中教授指出，“模型思想的本质是站在现实的立场上”“用现实的效果评价模型的功效”，体现了数学应用的广泛性。因此，要让学生体会模型思想的价值，应始终关注应用意识的感悟与发展，让“数学回归现实世界”，从一种情境到一类情境，从一个问题到一类问题，使模型思想不仅浸润于课堂学习，更“回声”于迁移应用及未来的学习。以“折线统计图”为例，不仅要培养学生的读图能力、判断与决策能力，还要培养学生自觉运用折线统计图进行交流与表达的意识和能力，从而把数学与其他学科、数学与生活融合起来建立“共鸣场”，实现“有意识地利用数学的概念、原理和方法解释现实世界的现象与规律，解决现实世界中的问题”。

在“折线统计图”教学中，笔者在学生建立折线统计图数学模型后，组织了两次“故事”的应用交流，使外化于形的折线统计图进一步内化于心。

应用故事1：判断，能否用折线统计图讲下面的“故事”。这其中包括两种不同的现实生活，一种是小东一学期单元小测情况，二是“五一节”景区游客人数情况。为更深入地感悟折线统计图的数学语言特征（升、平、降），讲述第一个故事时采用“变式”要求，即要求学生不画图、不说话，在规避常规折线统计图数学语言表达的同时，促使学生用“具有升、平、降的肢体动作语言”来表达数据信息，更直观形象地“画”出小东单元小测的变化情况，使学生在灵活表达中达成对折线统计图模型的深刻理解。讲述第二个故事时，则直接给出两位学生关于2021年“五一节”清源山景区每日游客人数预测的折线统计图（如图3、图4），让学生思考哪一幅图所讲的“故事”更合理。在不同意见的表达中，学生产生用数学的眼光“理论联系实际”的兴趣，懂得把联系生活现实作为判断依据。如5月6日不属于放假时间，家长要上班，学生要上课，游客人数应该变少，所以小明的预测更合理。通过两个不同情境类型的故事交流，让学生感受折线统计图应用的广泛性。

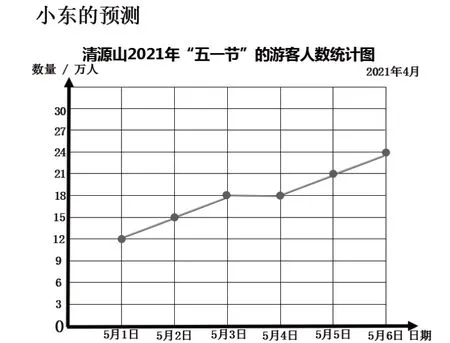
图3

图4

应用故事2：表达，如果这是有关你或家人的折线统计图，你希望它是一个怎样的“故事”（如图5）。学生从之前猜测他人的生活现实到关注自身的生活现实或生活期待，如希望父母工资收入越来越多、自己高兴的事越来越多，或家里的水电费越来越少、每天的作业越来越少等。学生感受到同一幅折线统计图虽然表达的内容并不相同，但可以表达一类同样趋势的事件，并在“哪一幅图更好”的追问中，感悟“都好，要看具体情况”，发展了分析、判断的理性精神。

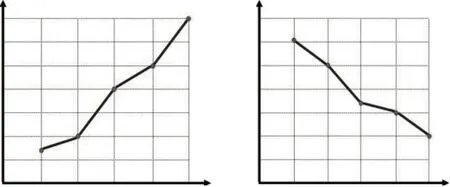
图5

数学的应用意识，不仅体现为课堂上的知识迁移，用数学的方法解决生活中的现实问题，还体现为将不同的形式运用于其他学科的综合学习中。

小学阶段模型思想的教学需有全程的眼光、全局的视野。模型思想要始终贯穿于数学学习的各个领域、各个内容。教师要使学生在学习过程中感悟模型意识、数据意识、应用意识，积累相关活动经验，从而使模型思想切实脱离“附属品一样永远停留在渗透层面”的困境，以师之“昭”达生之“明”，在讲好“故事”的同时，发展学生核心素养。