感悟推理思想 发展数学思维
——以“商的变化规律”为例谈推理思想教学
□李培芳
《义务教育数学课程标准(2022年版)》指出:“会用数学的思维思考现实世界是学生的核心素养之一,在小学阶段,学生数学的思维主要表现为运算能力和推理意识。”教师应当将发展学生的运算能力和推理意识贯穿于学生数学学习活动的全过程,使其融入数学学习的各个领域,以促进学生数学思维的发展。综观小学数学的教学内容可以发现,数学运算教学中充溢着推理思想,包含着大量演绎推理和归纳推理的过程,是学生学习推理方法、积累推理经验、发展推理意识、感悟推理思想的重要载体。本文管中窥豹,以“商的变化规律”为例,阐明在数学运算中,如何引领学生感悟推理思想,发展数学思维。
一、经历从特殊到特殊的推理过程,感悟类比推理思想
类比推理是从特殊到特殊的推理,其思维模式是由此类到彼类的联想。这种联想不仅需要知识的积累,而且要具有丰富的想象。想象与联想的思维方式是类比的方法,即如果两类事物具有许多相同的性质,就可以通过一类事物具有的性质联想另一类事物也具有相同的性质。
引领学生感悟类比推理的思想,前提是要为学生创造类比推理的机会。在“商的变化规律”内容的教学中,课伊始,教师创设了“孙悟空分香蕉”的情境(如图1),引导学生思考:第几次每只小猴子分得多?学生大多能想到,第一次比第二次分得多。教师追问:“你是怎么想的?”一般有三种想法。

图1
第一种是分析方法,因为小猴子的数量第一次比第二次少,所以第一次就分得多了。
第二种是举例方法,假如分的是6根香蕉,第一次分给3只猴子,每只猴子能分到2根,第二次分给6只猴子,每只猴子只能分到1根,所以是第一次每只猴子分得多。
第三种是类比方法,就像分蛋糕,人多了,分得就少了。
在这个过程中,学生的想法都是推理,虽然他们并没有严谨地表达自己推理的过程(教师也不应当作统一要求),但是学生头脑中的思考过程就是严谨的推理过程。值得一提的是第三种方法,学生运用的是典型的类比推理的方法。对第三种方法,教师给出如下的评价:“这个道理很简单,生活中很常见,确实是这样的,同样多的东西,分的人多了,每个人分到的东西肯定就少了。这是常识,每个人都懂。这个生活常识还可以帮助我们解决数学上的问题。”教师的评价里,暗含着对类比推理在方法上的引导和在价值上的倡导。
由此,教师创设的这个情境成了本内容教学重要的平台、依托和载体。这个看起来非常简单的情境,可以在学生理解问题出现困惑的时候,帮助他们进行类比推理。这个情境具有教学指导的价值,是一个巧妙的设计。
右心功能的评价指标主要包括RAA、RVDd、ΔIVC、RVESV、RVEDV及RVEF。本研究中比较了AF患者分别经RT-3DE和CU检测的右心功能指标,结果显示,RT-3DE检测结果中RVESV、RVEDV值明显高于CU检测值,RVEF值明显低于CU检测值,表明RT-3DE检测数据更好显示出患者的右心收缩功能减弱。
在接下来的探究环节中,教师让学生猜一猜(如图2):从上往下第1个笑脸背后的数可能是多少?有的学生认为是96,有的学生认为是24。在交流中,有学生说道:“可以用猴子分香蕉的例子来想,11变成22,就是猴子变多了,那么每只猴子分到的香蕉就会变少,所以96肯定不对,应该是24。”这个学生运用的就是类比推理。
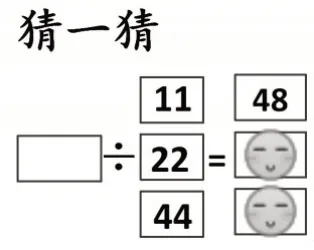
图2
类比推理是基于“联想”的推理,在思维方式上有“跳跃”“飞出去”的感觉,引导学生感悟类比推理思想可以从以下几方面着手:一是多为学生创造类比推理的机会,让学生不断积累类比推理的经验。二是外化学生类比推理的过程,让更多的学生看到“联想”与“想象”的过程。三是让学生感受类比推理的价值,类比推理的运用能让学生快速地发现方法和规律,从而有效地解决问题,使学生感受到数学思维的神奇美妙。
类比推理是追求“事实”的推理,是“发现”知识的推理,其结论具有或然性。在数学教学中,教师应当创设适宜的情境让学生学习类比推理,感受数学发现的“高峰体验”。
二、经历从一般到特殊的推理过程,感悟演绎推理思想
演绎推理是从一般到特殊的推理,其思维模式主要有三段论、完全归纳法、反证法等,演绎推理的思维基础是定义和命题。由于小学生处于具体运算阶段,在小学数学教学中定义和命题只要求学生理解,不要求学生作严格意义上的表述,这一点教师应特别注意。换言之,小学阶段学生演绎推理的培养应当“重实质而轻形式”。史宁中教授认为:“数学计算属于演绎推理,通过数学计算得到的结果是必然成立的。”数学运算教学是培养学生演绎推理的重要途径。
在“商的变化规律”的教学中,教师设计了如图3的“猜一猜”的活动,让学生猜测从上往下第1个笑脸背后的数是多少。有的同学认为是3,有的同学认为是12。这两种答案都是基于假定命题的演绎推理。
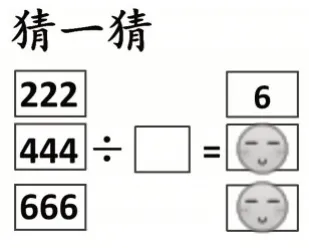
图3
认为第1个笑脸答案是3的同学,他们的推理过程是这样的。
大前提:除数不变,被除数乘几,商就除以几。(前一结论的负迁移)
小前提:本题中,除数不变,被除数乘2。
结论:商就除以2,所以答案是3。
认为答案是12的同学,其思维过程是一样的,也是演绎推理的过程。史宁中教授认为,学生在数学学习时,只要逻辑自洽,前后一致,即便结论错误,也是应当予以肯定的。这里强调的是推理本身的意义,从育人价值的角度看,推理意识、推理能力、推理思想之于一个人的意义是超越具体知识的。这一环节中认为答案是3的同学结论显然是错的,错在大前提,但其推理过程是严谨的。这样的过程虽然结论错误,但是对于学生形成重论据、合乎逻辑的思维品质是有益处的。
在揭晓第1个笑脸的答案是12之后,教师引导学生继续思考第2个笑脸背后是几。很多同学脱口而出“24”,这是教师有意设置的思维陷阱。虽然答案是错的,但是其思维过程仍然是严谨的演绎推理过程。错误出在小前提:被除数从444到666并非乘2,而是乘1.5,或与第一个算式作对比,被除数从222到666是乘3。在这样的过程中,学生一方面发展了推理意识和推理能力,同时也感悟到“推理结论正确的条件是大前提和小前提必须正确”。这些从经验中获得的感悟对于学生发展推理意识是非常重要的。
在本内容教学的最后,教师引导学生用数学的眼光,到生活中去寻找这样的规律。有的同学想到分蛋糕,有的同学想到食堂分餐等。随后,教师出示图4,让学生解释:“为什么会僧多粥少?”学生都能想到,一大锅粥的总量是被除数,它是不变的,来的和尚越多,就相当于除数变大,每个和尚分到碗里的粥相当于商,就会变小。这是演绎推理的过程。虽然学生的表达不是严谨的三段论,但是其推理过程是严谨的三段论。

图4
演绎推理是基于“形式”的推理,在思维方式上强调“逻辑”。教师引导学生感悟演绎推理思想,应注意以下几点:一是注重让学生进行充分的数学表达,彰显演绎推理逻辑的严密性,同时也要让学生在数学表达中完善自己的推理过程。二是注重让学生感悟演绎推理所获得结论的确定性,感受演绎推理的价值。三是注重让学生反思其推理过程,强化演绎推理的模式,在不断地强化中实现内化。
演绎推理是追求“形式”的推理,是“验证”知识的推理,其结论具有必然性。在数学教学中应当尽量为学生创造演绎推理的机会,让学生经历数学证明的历程。
三、经历从特殊到一般的推理过程,感悟归纳推理思想
归纳推理是从特殊到一般的推理,是人们在日常生活中经常使用的推理形式,是一种比演绎推理更为“自然”的推理。归纳推理的本质是从经验过的东西中推断未曾经历过的东西,从事物的过去推断事物的未来,是一种创造性的思维模式。现行的小学数学教材中,大多数规则(定律、性质、法则、公式等)都是通过归纳推理得出的。本文所阐述的归纳推理是基于一个类的归纳推理(以与基于两个类的类比推理区分开来)。
在“商的变化规律”的教学中,让学生猜一猜算式的结果,得出图5的三个算式后,教师引导学生观察算式中被除数、除数和商,思考“什么变了,什么没有变”。学生通过观察、比较,发现三个算式都是“被除数不变,除数乘2,商就除以2”,由此提出以下猜想。

图5
猜想一:是不是在所有的除法算式中,被除数不变,除数乘2,商就除以2。
猜想二:是不是在所有的除法算式中,被除数不变,除数乘几,商就除以几。
这两个猜想是通过归纳推理产生的,它是从几个具体算式直接推断一类算式的性质。紧接着,教师引导学生用举例的方式,对自己的猜想进行验证,最终获得结论。当然,最终结论仍然是建立在有限的例子之上,而非穷尽所有例子。由于小学生的认知发展水平,学生往往会将不完全归纳的结论视为必然性结论,这是学习的阶段性决定的。
史宁中教授指出:“归纳推理的思维基础是类,其思维过程是动态的。”以下教学过程很好地体现了这一观点。
在得出第一条规律“被除数不变,除数乘几,商就除以几”之后,教师引导学生思考,这里的乘几到底是乘几?学生回答,乘任何数都可以。教师通过有序的“对口令”的方式追问:如果除数乘5(商就除以5);除数乘4(商就除以4);除数乘3(商就除以3);除数乘2(商就除以2);除数乘1(商就除以1)……至此,教师戛然而止,不往下说了,静静地看着学生。不一会儿,就有学生反应过来,急忙说:“不行,乘0就不行了。”“乘0,除数变成0,就没有意义了。”教师引导学生思考:“辛辛苦苦发现的规律,被这个0轻而易举就给推翻了,怎么办?”学生们经过讨论,一致认为,只要在结论中加上“0除外”就可以了。此时,教师称赞学生:“真聪明啊,我们退一步,不要任何数了,给任何数加个限制——0除外,就可以了。”
在这一教学过程中,我们可以直观地看到,归纳推理的思维过程是动态的,当其思维对象的整个大类没有满足相同特征或共同属性时,可以缩小类。即上述教学中的将“任何数”的这一大类缩小为“0除外的任何数”,从而确保推理结果在当前例子上的正确性。
同样,在第二条规律的教学中,学生通过“除数不变的三个算式”,得出结论“在除法算式中,除数不变时,被除数乘几,商就乘几”的过程,也是借助归纳推理,不再赘述。
归纳推理是基于“经验”的推理,在思维方式上有“谨慎”而又“果敢”的特征。在进行归纳推理的过程中,学生在无法穷尽一切的情况下,总是努力找出各种不同的情况,以使结论更“可靠”,然而不完全归纳推理终究是或然性推理,其得出结论的过程是需要几分果断的。由此可见,不同的推理方式有不同的育人价值。引导学生感悟归纳推理思想,应注意以下几点:一是不轻易下结论,要将结论建立在尽量多的例证上。二是对结论要保持警惕与审慎,猜想之后要验证应当成为一种思维习惯。三是学会用“缩小类”或“弱化性质”的方式调整归纳推理的结论。
归纳推理是追求“事实”的推理,是“发现”知识的推理,其结论具有或然性。教师在数学教学中应当尽量为学生创造归纳推理的机会,让学生感受数学思维的“理智欢乐”。
综观本内容的设计,最为巧妙的是将演绎推理与合情推理运用在学习的整个过程中,甚至让学生在一个问题的思考中,同时运用不同的推理方法。以第一条规律的教学为例,在图6中,当学生想出从上往下第1个笑脸背后的数是24,借助的是类比推理,其思维过程是这样的:除数变大就相当于“孙悟空分香蕉”时“猴子变多了,每只猴子分得的香蕉会变少”。由此类比出这样的假定性命题:“被除数不变,除数乘2,商反而除以2”。

图6
从这个假定的命题出发,除数乘2,商应该是48÷2,得24。即第1个笑脸背后的数是24,这里借助的是演绎推理。
紧接着思考第3个笑脸背后的数,仍然是基于假定性命题的演绎推理。
最后通过三个算式形成猜想,并举例验证的过程,借助的是归纳推理。
本文以“商的变化规律”的教学为例,谈如何引导学生经历“推理思想的感悟、推理意识的培养和数学思维的发展”的过程。值得我们进一步思考的是,数学课程中所有内容的学习都需要渗透推理思想。教师应当在数学教学中帮助学生积累数学推理的经验,感受数学推理的价值,引导学生感悟数学推理的思想,发展学生的数学思维,逐步让学生学会用数学的思维思考现实世界。

