代数群上由模糊(拟)伪度量诱导的拓扑
涂金基,谢利红
(1.江门职业技术学院 数学教研室,广东 江门 529000;2.五邑大学 数学与计算科学学院,广东 江门 529020)
1 引言与记号
拓扑代数是目前国际上研究的热点方向之一,拓扑群、仿拓扑群以及半拓扑群等是其中的主要研究对象.
定义1[1]12设(G,×)是一个抽象的群,τ是G上的一个拓扑,
1)如果群G上的乘法运算×:G×G→G关于拓扑τ是左连续的,则称(G,τ)为左拓扑群;
2)如果群G上的乘法运算×:G×G→G关于拓扑τ是右连续的,则称(G,τ)为右拓扑群;
3)如果群G上的乘法运算×:G×G→G关于拓扑τ是联合连续的,则称(G,τ)为仿拓扑;
4)设(G,τ)是一个仿拓扑群,如果G中的求逆运算也是连续的,则称(G,τ)是一个拓扑群.
本文简记(G,τ)为G.显然每一个拓扑群都是一个仿拓扑群;每一个仿拓扑群都是一个左拓扑群和右拓扑群.
作为度量的推广,Kramosil等[4]引入了模糊度量.研究表明,模糊度量在研究模糊结构方面是个强有力的工具[3,5-7];一些拓扑学家应用模糊度量研究拓扑群[8-10]时发现:某些特殊的模糊(拟)度量将使一些拓扑代数结构变成更强的拓扑结构.例如:
定理1[10]81设G是一个抽象群以及(M,*)是G上的一个左不变的模糊拟伪度量,如果(G,M,*)是一个模糊拟伪度量右拓扑群,那么(G,M,*)是一个模糊仿拓扑群.
本文主要研究抽象群上由一些特殊的模糊(拟)伪度量诱导的拓扑.下面介绍本文用到的定义和符号.
定义2设X是一非空集合,d:X×X→[0,+∞)是一个函数:
1)若d满足:i)对任意的x∈X有d(x,x)=0和ii)对任意的x,y,z∈X有d(x,z)≤d(x,y)+d(y,z),则称d是X上的一个拟伪度量;
2)如果d是X上的一个拟伪度量且满足:iii)对任意的x,y∈X有d(x,y)=0当且仅当x=y,则称d是X上的一个拟度量;
3)如果d是X上的一个拟伪度量且满足:iv)对任意的x,y∈X有d(x,y)=d(y,x),则称d是X上的一个伪度量;
4)如果d是X上的一个伪度量且满足上面的条件iii),则称d是X上的一个度量.
设X是一非空集合,d是X上的一个拟伪度量,记其中对任意的x∈X,ε>0有:那么可知,τd是X上的一个拓扑,而且βd是τd的拓扑基.
定义3[11]318如果二元运算*:[0,1]×[0,1]→[0,1]满足如下条件,则称*是一个连续的t-模:
1)*满足结合律和交换律;2)*是连续的;3)对任意的a∈[0,1]有a*1=a;4)对任意的a,b,c,d∈[0,1],如果有a≤c,b≤d,则有a*b≤c*d.
已知对于任意的连续t-模*有:*≤˄,其中˄是如下定义的连续t-模:

定义4[2]30设X是一集合,*一个连续t-模以及M是X×X×[0,+∞)上的一个模糊集,如果对于任意的x,y,z∈X和t,s>0有(M,*)满足:1)M(x,y,0)=0;2)M(x,x,t)=1;3)M(x,z,t+s)≥M(x,y,t)*M(y,z,s);4)M(x,y,_):[0,+∞)→[0,1]是左连续的,则称(M,*)是X上的一个模糊拟伪度量;如果(M,*)还满足:5)M(x,y,t)=M(y,x,t)对任意的x,y∈X和t>0,则称(M,*)是X上的一个模糊伪度量.
定义5[10]80设(M,*)是群G上的一个模糊伪度量,对任意的a,x,y∈G和t>0,如果:
1)(M,*)满足M(x,y,t)=M(ax,ay,t),则称(M,*)是左不变的;
2)(M,*)满足M(x,y,t)=M(xa,ya,t),则称(M,*)是右不变的;
3)如果(M,*)既是左不变的,又是右不变的,则称(M,*)是不变的.
2 主要结果
定义6[2]31设X是一集合,(M,*)是X上的一个模糊(拟)伪度量,那么称(X,M,*)为一个模糊(拟)伪度量空间.
设(X,M,*)是一个模糊(拟)伪度量空间,记其中对任意的有:
引理1[8]110设(X,M,*)是一个模糊拟伪度量空间,那么τM是X上的一个拓扑,而且βM构成τM的一个拓扑基.
定理2设G是一个抽象群,(M,*)是G上的一个模糊拟伪度量,则:
1)如果(M,*)是左不变的,那么(G,τM)是一个左拓扑群;
2)如果(M,*)是右不变的,那么(G,τM)是一个右拓扑群;
3)如果(M,*)是不变的,那么(G,τM)是一个仿拓扑群.
证明设e是群G的单位元,记Be={M(e,ε,t):ε∈(0,1),t>0}.
1)根据引理1可知τM是G上的一个拓扑,下面证明群的乘法运算关于τM是左连续的.任取x,y∈G和包含xy的一个开集U,根据引理1,则存在某一ε∈(0,1)和t>0有xy∈BM(xy,ε,t)⊆U.又因为M是左不变的,因此有xBM(y,ε,t)=BM(xy,ε,t)⊆U,显然BM(y,ε,t)是y的开邻域,因此证明了群G的乘法运算关于τM是左连续的,从而(G,τM)是一个左拓扑群.类似可证2).
3)根据引理1可知τM是G上的一个拓扑,下面证明群的乘法运算关于τM是联合连续的.任取x,y∈G和包含xy的一个开集U,根据引理1,则存在某一ε∈(0,1)和t>0有xy∈BM(xy,ε,t)⊆U.因为t-模*是连续的,所以对于上面的ε可以找到ε0∈(0,1)满足(1-ε0)*(1-ε0)>1-ε.

从而xy∈BM(e,ε,t),这就证明了显然是x的邻域、是y的邻域,下面只需证明即可.
注意到(M,*)既是左不变的又是右不变的,因此很容易验证:对任意的成立,所以有:得证.
(X,d)是一个(拟)伪度量空间,定义X×X×[0,+∞)上的模糊集那么(Md,˄)就是X上的一个模糊(拟)伪度量,从而对于任意的t-模*有(Md,*)是X上的一个模糊(拟)伪度量.已知在X上由(Md,*)诱导的拓扑τM和由d诱导的拓扑τd是一样的,所以根据定理2很容易得到以下结论:
推论1设G是一个抽象群,d是G上的一个拟伪度量,则:
1)如果d是左不变的,那么(G,τd)是一个左拓扑群;
2)如果d是右不变的,那么(G,τd)是一个右拓扑群;
3)如果d是不变的,那么(G,τd)是一个仿拓扑群.
定理3设G是一个抽象群,(M,*)是G上的一个模糊伪度量,如果(M,*)是不变的,那么(G,τM)是一个拓扑群.
证明因为每一个模糊伪度量都是一个模糊拟伪度量,因此根据定理2的3)可知(G,τM)是一个仿拓扑群.下面只需证明G中的求逆运算是连续的.
任取x∈G以及包含x-1的开邻域U.根据引理1,则存在某一ε∈(0,1)和t>0有x-1∈BM(x-1,ε,t)⊆U.下面只需证明BM(x,ε,t)-1⊆U即可.任取z∈BM(x,ε,t),由于(M,*)是不变的模糊伪度量,从而有:
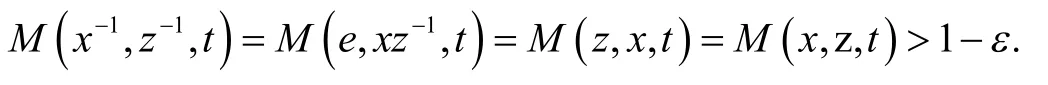
这就证明了BM(x,ε,t)-1⊆U,所以(G,τM)是一个拓扑群.
由定理3可以直接得到以下结论:
推论2设G是一个抽象群,d是G上的一个伪度量,如果d是不变的,那么(G,τd)是一个拓扑群.

