浅析放缩式在不等式证明中的应用

◎孟丽萍

(青海师范大学数学与统计学院,青海 西宁 810008)

一、引 言

数学方法是指通过运用事物之间的各种位置和空间关系抓住事物的本质，对各种已知条件和推出的条件加以整合、组织，使其推出结论的过程中所运用的手段、模式、方式等例如待定系数法、配方法、向量法、放缩法、换元法、演绎法、反证法等，它们都是人们经过长期刻苦地专研、认识和实践研究出来的解决问题的“门路”和“程序”放缩法是数学方法中重要的一种，能够将数学问题化难为易、化繁为简

放缩法，顾名思义就是把代数式中的某些部分恰当地放大或缩小，得到相应的不等式，研究它的性质，以达到解题的目的举个例子：要证明+2+2恒为正数，就要证明+2+2>0，很多人会通过=1>0且=-4=4-8=-4<0 来证明=+2+2的函数图像在轴上方，从而恒为正数但我们可以发现，+2+2=(+1)+1，又因为完全平方是非负数，所以+2+2=(+1)+1≥1>0，所以+2+2恒为正数这个过程就用到了简单的放缩思想，即要证明>，如果已知>，那么我们只要证明≥，则可以证明>这里要注意不等号的方向只有同向才能进行传递

放缩式是放缩法的重要组成部分，是放缩法的“骨肉”用好放缩法的关键在于灵活运用放缩式，我们既然想去放缩一个式子来证明不等式，那最基本、最重要的就是掌握一些重要的放缩式

二、放缩式

这里将放缩式分为基本放缩式和变形放缩式基本放缩式也就是常说的“不等式串”，大部分放缩式都由它变形而来，是必须掌握的放缩式

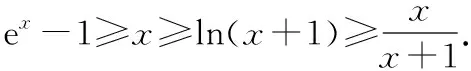
变形放缩式大部分是由基本放缩式灵活变形而来的

1e-1≥⟹e≥+1⟹e-1≥(把-1 看成整体)⟹e≥e

2≥ln(+1)⟹-1≥ln

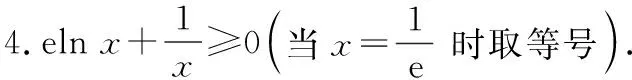
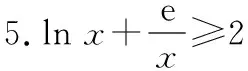
6-≥-1(当=1时取等号)

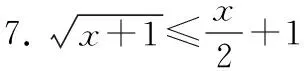
三、放缩小技巧

(一)不等号的方向

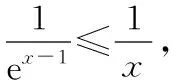
1求证：e-2eln≥e(-2+2)

要直接证明这个式子可能有点难度，不妨分几步来想：

①两边约去e，即证e-1-2ln≥-2+2；

②我们可以发现式子右边是二次函数，左边是指数和对数式，从右边到左边证明会有点难，故不妨从左往右证明推；

③但我们只能往小处放(根据题目要求，往小于号处走)，又发现ln前边有负号，故不等号方向问题也解决了，即-ln≥-+1；

④则有e-1-2ln≥·+2(1-)=-2+2

e-2eln=e(e-1-2ln)

≥e[+2(1-)]=e(-2+2)

(二)整体代换

整体代换使用的是数学中的整体思想，比如e-1≥⟹e≥+1⟹e-1≥，这个式子中便运用了此方法，学会将已知的放缩式变更为解题需要的放缩式很重要

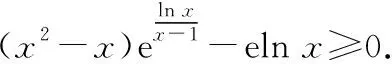
我们同样分成几步来考虑：

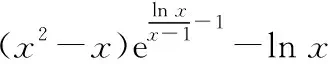
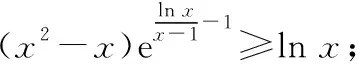
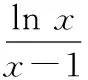
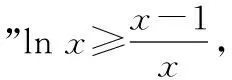
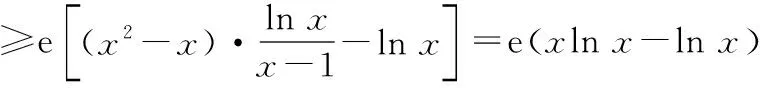
≥e(ln-ln)=0

(三)调整次数

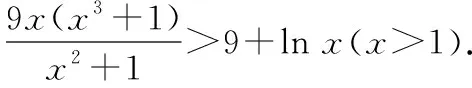
我们知道，当>1时，有>，再利用变形放缩式-1≥ln即可求解

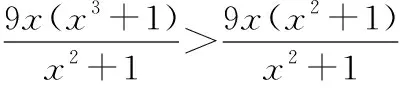
=9>9(ln+1)=9+9ln

>9+ln

(四)上幂

“上幂”的精髓在于把相乘的式子化为对数式，比如e=e+ln ≥+ln+1(>0),这个式子巧妙的地方在于将e变为e+ln ，然后运用 e≥+1这个放缩式进行变形

四、放缩式的应用

放缩式的应用极为广泛，在求函数极值、数列求和以及不等式证明中经常会用到放缩法，是高考数学命题的热点与难点，掌握基本放缩式与变形放缩式对于快速、准确地解题有很大帮助下面，我们从导数放缩和数列放缩两方面对放缩式在不等式证明中的应用进行分析

4已知()=e+-,()=ln(+1)+2，当≥1时，证明：()≥()-

因为≥1，所以e+≥e+1，利用放缩式e≥+1以及放缩小技巧中的整体代换思想，可得出e+1≥(+1)+1，即可得证

原式即证e+≥ln(+1)+2

∵e+≥e+1≥(+1)+1=+2≥ln(+1)+2,

∴()≥()-

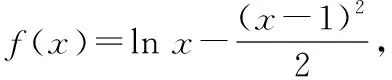
此题利用放缩式-1≥ln即可得证

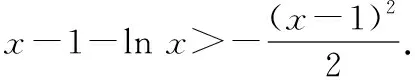
∴()<-1

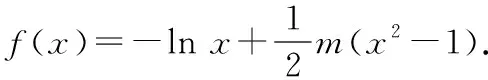
(1)讨论()的极值；

此题有一定难度，第二问证明充分性时运用了在(1,+∞)上e-1≥和≥

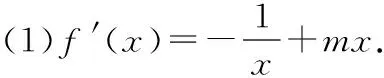
①当≤0时，′()<0，()在(0,+∞)上单调递减，无极值；

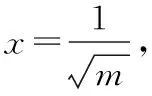
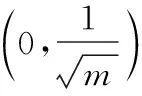
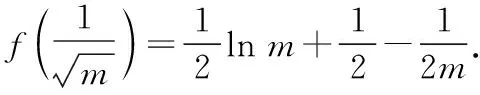
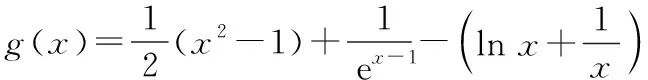
故()>(1)=0

综上所述，的最小值为1

7已知数列{}的首项为1，为数列{}的前项和，+1=+1，其中>0，∈

(1)若2,,+2成等差数列，求的通项公式；

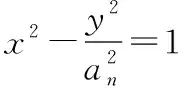
(1)由题+1=+1……①，

可知当≥2时，=-1+1……②，

两式相减，可得+1=，

即从第二项开始是公比为的等比数列

当=1时，代入①式，可得+=+1，

∴=，即是首项为1、公比为的等比数列

根据2,,+2成等差数列，由等差数列性质，可得2++2=3+2=2，

由题，>0，可知=2，∴=2-1,∈

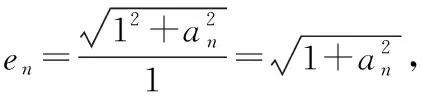
由(1)可得,{}为首项为1、公比为的等比数列，

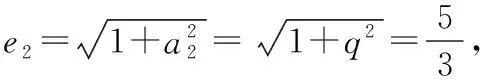
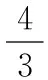
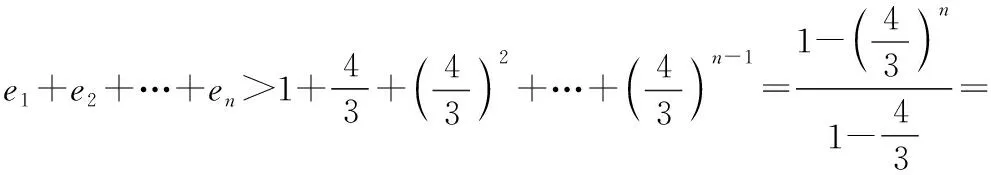
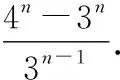
原式得证

五、结 论

放缩式可以与很多知识内容相结合，学生要具有较强的观察能力和应变能力，才能对式子进行合理的放缩放缩法以及放缩式的教学有利于增强学生分析和解决问题的能力及逻辑思维能力，在合理放缩的过程中也能体现学生的创造力和探索能力正所谓“授人以鱼，不如授人以渔”，数学方法就是“渔”的工具、策略数学方法的教学适应了科技不断发展、知识不断更新的需要，它有利于知识的迁移和培养学生的数学思维品质，学生学会数学方法，才能在解决数学问题时举一反三