浅析集合论中的等价关系及其判断方法
郭丽君
(兰州博文科技学院电信工程学院,兰州730101)
1 引 言
离散数学课程是计算机学科各专业核心课,在课程体系中占有重要地位,该课程由集合论、代数系统、图论、数理逻辑四部分内容组成,集合论是所有章节内容的基础,因此从集合论出发,通过集合的基本定义和运算、有序组和笛卡尔乘积、关系的定义和性质、次序关系、等价关系[1-2],由浅入深,使得学生对集合有了更全面、更系统的认识,其中等价关系更是将关系和集合更紧密的联系起来,通过等价关系能更深刻的认识一个集合.但通过等价关系的定义判断一个关系是否是等价关系,在关系较为复杂的情况下,判断不太准确,通过写出等价关系的关系矩阵[3-4],用矩阵理论去判断等价关系更为有效,同时为进一步通过计算机编程手段判断等价关系奠定了理论依据,这也是相关教科书上没有提到的.
2 划分与块
1.1 基本概念
在集合论中,关系作为笛卡尔集合的子集,是集合论的一个重要组成部分,并不是每个集合都能称为关系,只有元素形式为有序偶的集合才能称为关系.
定义1设非空集合A与B,定义集合R={(ai,bi)|ai∈A,bi∈B}为集合A到B的一个关系.其中集合A称为关系R的定义域,集合B称为关系R的值域,一般情况下有R⊆A×B.定义在集合A与B上的若干个关系,按其性质可归类为次序关系、等价关系等,其中要掌握等价关系,划分与块的概念是一个非常重要的定义,掌握划分的思想是进一步理解块、等价类等概念的基础.
定义2对非空集合E,有A1,A2,…,An都是集合E的子集,且满足以下两个条件:
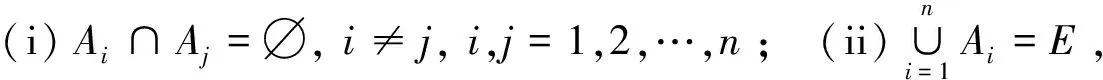
实际上,关于划分和块的概念在生活中随处可见,如集合E={计算机科学班全体学生},可以按照{男生}和{女生}将集合E划分成两块,但这只是最普通的一种划分,如果按照学生的籍贯来划分,又可将E划分成{甘肃籍学生}{陕西籍学生}{吉林籍学生}等多块,又或是以学生所在宿舍来划分,以该班学生共40人为例,至少可以将集合E划分成7块,还可以根据对学生考察的不同目的进行其他方式的划分,但无论是怎样的划分,每种划分方式下得到的块都满足两两互斥性,同时所有块的并集正好覆盖集合E.除以学生作为集合进行划分外,在实际生活中如超市的所有货品、车站的候车区、小吃街的所有摊位组成的集合,都符合划分和块的概念,也就是说,划分与块的概念在生活中随处可见,划分将庞大的集合变得更确切、更具体,块中的元素更明了、更清晰、更统一.而在集合X上建立一个等价关系R后,该等价关系R也能对集合X产生一个划分.
1.2 等价类对集合的划分
定义3等价关系是指一个定义在集合X上的关系R,如果能满足自反性、对称性和传递性,则关系R称为等价关系.
在集合X上定义一个等价关系R,可进一步对集合X进行划分,划分得到的块称为等价类,具体定义如下:
定义4设R是集合X上的等价关系,对任一x∈X可以构造一个X的子集[x]R,称为x对于R的等价类,记为[x]R={y|y∈X,xRy},也即[x]R={y|y∈X,(x,y)∈R}.
在实际生活中,存在很多等价关系,如老乡关系、同学关系、同事关系等,在整数集合上,定义的一种同余关系也为等价关系,即R={(x,y)|x-y能被m整除,x,y,m∈,m≠0}.
下面通过分别验证该关系具有自反性、对称性、传递性来说明关系R为等价关系.
证首先,对任意x∈,都有x-x=0能被m整除,即∀(x,x)∈R,所以关系R满足自反性.
其次,若有(x,y)∈R,也就是x-y能被m整除,那么y-x=-(x-y)也能被m整除,则有(y,x)∈R,所以关系R满足对称性.
最后,若有(x,y)∈R,(y,z)∈R,也就是x-y能被m整除且y-z能被m整除,那么x-z=(x-y)+(y-z)也能被m整除,则有(x,z)∈R,所以关系R满足传递性.
综上可知,关系R为等价关系.
当(x,y)∈R,x≠y时,对整数x,y,m之间的关系进一步分析,发现元素x,y同时除以m时,商不同但余数完全相同,因此将关系R比较形象的称为以m为模的同余关系,记为x≡y(modm).
={x|x=2n,n∈}∪{x|x=2n+1,n∈}且{x|x=2n,n∈}∩{x|x=2n+1,n∈}=∅,
对数字有了负数的定义后,整数集合又可以划分为正整数集合、零和负整数集合,即
=+∪{0}∪-且+∩{0}=∅,+∩-=∅,-∩{0}=∅.
通过对整数集合现有的认识,以上是两种最常见的划分方式,看起来也是最容易理解和被接受的划分,但存在的问题是,上述方法无论是将整数划分成两块还是三块,每个块中整数的特点都不太明显,因为整数中既有奇数又有偶数,既有正数又有负数,现有的常规的两种划分只是对整数集合最初步的理解和认识.
利用同余关系,可以按照模m的取值将整数集合进行任意划分,且划分后的每一块都保留整数的特点,即既有偶数又有奇数,既有正整数又有负整数.如当m=4时,
R={(x,y)|x-y能被4整除,x,y∈},
R所构成的等价类分别为[0]R={…,-8,-4,0,4,8,…},[1]R={…,-7,-3,1,5,9,…},
[2]R={…,-6,-2,2,6,10,…}, [3]R={…,-5,-1,3,7,11,…},
显然四个块满足两两互斥性,同时四个类的并集正好覆盖住集合,由此在集合上建立模为4的同余关系后,得到了整数集合的又一个划分,将整数集合划分成了4块,以此类推,以模m的取值决定可以将整数集合进行任意划分,显然对整数集合的这种划分更科学.
例1设在集合A={1,2,5,8,10,13,15,16}上建立以3为模的同余关系R,将集合A进行划分.
解关系R的等价类为[1]R={1,10,13,16},[2]R={2,5,8},[15]R={15},因此集合A此时被划分成了3块,即A={[1]R,[2]R,[15]R},记为A的商集A/R.
1.3 由集合的划分产生等价关系
反过来,任给一个集合的划分,也会产生一个等价关系,等价关系和划分时刻都是同时存在,相互依存的.
例2设集合A={a,b,c,d,e,f}的一个划分是A1={a,b,c},A2={d},A3={e,f},则由此划分产生的等价关系为R={(a,a),(b,b),…,(f,f),(a,b),(b,a),(a,c),(c,a),(b,c),(c,b),(e,f),(f,e)}.
显然构造的关系R是一个等价关系,实际上R=(A1×A1)∪(A2×A2)∪(A3×A3),对任一定义在集合A,B上的关系R,一般情况下,R⊆A×B,若有R=A×B,则此关系R称为定义在集合A,B上的全关系,已知一个集合的划分,对应的等价关系实际上是各块与自身全关系的一个并集,但等价关系不一定是全关系.
从疑点数据表中可知:在重度用电客户簇中,有一个疑点用户,在轻度用电客户簇中有9个疑点用户都可能存在偷电等情况的发生。经过实际有关人员对这些用户的调查,确实发现存在问题。实验结果表明该算法能够为内部审计提供审计依据,提高了工作效率。
3 等价关系与全关系
一个关系R如果是自反的、对称的、传递的,则该关系称为等价关系,而全关系的性质也要求关系满足自反的、对称的、传递的,那么等价关系一定是全关系吗?实则不然.
实际上,全关系一定是等价关系,但等价关系不一定是全关系,而由等价关系所构成的等价类形成的关系是全关系.
如果对等价关系按照等价类画出关系图的话,那等价关系和全关系之间的联系更显然,也更能体现出块的价值和作用,如画出例1的关系图如下:

图1 例1的关系图
在例1中将集合A={1,2,5,8,10,13,15,16}通过以3为模的同余关系R划分成了三块,对应的关系R显然不是全关系,因为至少可以看出(1,2)∉R,而按照等价类画出关系R的关系图,对应的三个类的关系图均是全关系,因此,全关系一定是等价关系,而等价关系不一定是全关系,但是按照类的划分对应的关系一定是全关系,也可以理解为在一个等价关系中包含着若干个全关系,有几个等价类就有几个全关系.
4 等价关系的判断
全面理解了等价关系之后,对一个给定的关系还要学会判断该关系是否是等价关系,如果通过定义观察关系是否有自反性、对称性、传递性的方法进行判断,对含有元素较少的关系可能比较有效,但对于较为复杂的关系来说用定义观察的方法得到的结论就不太准确了,通过引入关系矩阵和矩阵的布尔运算可以解决这一问题,用关系矩阵判断一个关系是否是等价关系也更具科学性,同时用矩阵理论判断等价关系也为进一步利用计算机编程进行等价关系的判断奠定了理论基础.
定义5设定义在集合X={a1,a2,…,an}上的关系R,定义其关系矩阵为An=(aij)n,其中
由此得到与一个与关系R完全对应的n阶方阵,且该方阵为布尔方阵.
用矩阵An的特点来说明对应的关系R是否是等价关系比较客观,且容易判断,有以下定理:
证首先,对应的关系矩阵An满足aii=1,i=1,2,…,n,即对角线上的元素均为1,则说明∀ai∈X,都有(ai,ai)∈R,根据自反性的定义,关系R是自反的.
其次,如果关系矩阵An是一个对称矩阵,则An满足aij=aji,i,j=1,2,…,n,即说明∃(ai,aj)∈R,则必有(aj,ai)∈R,根据对称性的定义,关系R是对称的.





综上所述,关系R满足自反性、对称性、传递性,所以关系R是等价关系,定理得证.
例3判断定义在集合X={a,b,c,d}上的关系R={(a,a),(b,b),(c,c),(d,d),(a,c),(c,a)}是否是等价关系.
证该关系R比较简单,用定义可以直接判断出关系R是等价关系,我们用矩阵理论加以验证,关系R对应的关系矩阵为

显然关系矩阵A是对称矩阵,对角线上元素均为1,且A(2)=A,因此关系R是等价关系.
5 结 论
在离散数学中关系是个非常重要的概念,是集合论中学习的重点也是难点,而关系性质的判定如果只局限于概念判定法,势必会影响后续学习,而且概念判定只适用于简单形式的关系,对复杂的关系利用概念判断不一定有效,也显得不那么科学.等价关系的判定,特别是其中关系传递性质的判定,对于学生来说,不是那么容易理解,在关系中元素众多的情况下更是难以判断,通过使用关系矩阵计算方法实现对等价关系的判定,既使得判定工作具有很好的可计算性,也具有更高的科学性,同时也为进一步利用计算机编程辅助手段判断关系的性质,判断关系是否为等价关系提供了可靠的理论依据,对于离散数学的教学也具有较好的参考价值.但必须要提的是,此处关系传递性的判断是基于等价关系的前提下,也就是关系本身既有自反性也有对称性,用定理中的矩阵理论判断传递性是有效的,对其他关系传递性的判断是否仍然有效还要进一步探讨.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.

