一个与Wallis不等式有关的单调增加数列
杨天虎
(酒泉职业技术学院新能源工程系,甘肃酒泉735000)
1 引 言
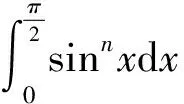


2 预备知识
2.1 基本公式[4]

(1)
(2)
当n≥2时,由(1)和(2)式得
(3)
2.2 引理
设有函数
f(x)

(4)
则当x>2时,f(x)∈(1,+∞)为严格单调减少函数.

3 证明定理
3.1 数列{pn}的极限
由(1)和(2)式得
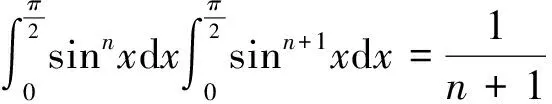
(5)
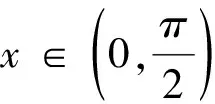
代入(5)式得

即
同理可得
所以
由此可得
(6)
3.2 数列{pn}的单调性

因
(n-1)2(256n4+64n3+848n2+200n+105)[256(n-2)4-64(n-2)3+848(n-2)2-200(n-2)+105]
=65536n10-655360n9+3084288n8-8945664n7+18165504n6-27793920n5+30402272n4-19415936n3
+5603265n2-1403010n+893025.
n(n-2)(256n4-64n3+848n2-200n+105)[256(n-2)4+64(n-2)3+848(n-2)2+200(n-2)+105]
=65536n10-655360n9+3084288n8-8945664n7+18165504n6-27793920n5+30402272n4-19415936n3
+5603265n2-1403010n.
所以
其中n≥3,由(4)式得
(7)

所以,{Jn}为严格单调减少数列.
由(6)式得

p2n-1 (8) 所以,{Kn}也为严格单调减少数列. p2n (9) 由(8)和(9)式得 p2n-1 (10) 由定理的结论(i),可得 则 (11) 同时 (12) 则 (13) 由(11)和(13)式得 (14) 定理的结论(ii)得证,定理证毕. 设 因 UnSn=(256n4-64n3+848n2-200n+105)(n+1)(256n4+960n3+2192n2+2328n+945) =65536n9+294912n8+946176n7+1935360n6+3005184n5+3362688n4+2141984n3 +621360n2+154665n+99225, VnRn=n(256n4+64n3+848n2+200n+105)(256n4+1088n3+2576n2+3112n+1473) =65536n9+294912n8+946176n7+1935360n6+3005184n5+3362688n4+2141984n3 +621360n2+154665n. 所以,(14)式的估值误差为 (15) 文献[1]给出的不等式为 (16) 文献[2]给出的不等式为 (17) 文献[3]给出的不等式为 (18) 比较(16)和(18)式,可得 可以看出,(18)式优于(16)式. 比较(14)和(17)式,可得 可以看出,(14)式优于(17)式. 从估值误差上看,显然(14)式均优于(16)-(18)式. 由(1)和(14)式得 (19) 显然,(19)式优于由(1)式与(16)-(18)式得出的Wallis不等式,同时也优于文献[5-7]给出的Wallis不等式,具体分析讨论见文献[3],这里不再赘述. 由(2)和(14)式得 (20) 注 在Mathematica软件下计算的部分结果 In[1]∶=Expand[(x-1)2(256x4+64x3+848x2+200x+105)(256(x-2)4-64(x-2)3 +848(x-2)2-200(x-2)+105)] Out[1]=893025-1403010x+5603265x2-19415936x3+30402272x4-27793920x5+18165504x6 -8945664x7+3084288x8-655360x9+65536x10 In[2]∶=Expand[x*(x-2)(256x4-64x3+848x2-200x+105)(256(x-2)4+64(x-2)3 +848(x-2)2+200(x-2)+105)] Out[2]=-1403010x+5603265x2-19415936x3+30402272x4-27793920x5+18165504x6 -8945664x7+3084288x8-655360x9+65536x10 In[3]∶=Expand[256(x+1)4+64(x+1)3+848(x+1)2+200(x+1)+105] Out[3]=1473+3112x+2576x2+1088x3+256x4 In[4]∶=Expand[256(x+1)4-64(x+1)3+848(x+1)2-200(x+1)+105] Out[4]=945+2328x+2192x2+960x3+256x4 In[5]∶=Expand[(256x4-64x3+848x2-200x+105)(x+1)(256x4+960x3+2192x2+2328x+945)] Out[5]=99225+154665x+621360x2+2141984x3+3362688x4+3005184x5+1935360x6 +946176x7+294912x8+65536x9 In[6]∶=Expand[x*(256x4+64x3+848x2+200x+105)(256x4+1088x3+2576x2+3112x+1473)] Out[6]=154665x+621360x2+2141984x3+3362688x4+3005184x5+1935360x6 +946176x7+294912x8+65536x9 In[11]∶=Expand[256(2x)4-64(2x)3+848(2x)2-200(2x)+105] Out[11]=105-400x+3392x2-512x3+4096x4 In[12]∶=Expand[256(2x)4+64(2x)3+848(2x)2+200(2x)+105] Out[12]=105+400x+3392x2+512x3+4096x4 In[13]∶=Expand[256(2x)4+1088(2x)3+2576(2x)2+3112(2x)+1473] Out[13]=1473+6224x+10304x2+8704x3+4096x4 In[14]∶=Expand[256(2x)4+960(2x)3+2192(2x)2+2328(2x)+945] Out[14]=945+4656x+8768x2+7680x3+4096x4 In[15]∶=Expand[256(2x+1)4-64(2x+1)3+848(2x+1)2-200(2x+1)+105] Out[15]=945+4656x+8768x2+7680x3+4096x4 In[16]∶=Expand[256(2x+1)4+64(2x+1)3+848(2x+1)2+200(2x+1)+105] Out[16]=1473+6224x+10304x2+8704x3+4096x4 In[17]∶=Expand[256(2x+1)4+1088(2x+1)3+2576(2x+1)2+3112(2x+1)+1473] Out[17]=8505+25104x+29504x2+16896x3+4096x4 In[18]∶=Expand[256(2x+1)4+960(2x+1)3+2192(2x+1)2+2328(2x+1)+945] Out[18]=6681+21232x+26432x2+15872x3+4096x4 致谢在此感谢审稿老师给本文的宝贵意见.
3.3 改进的双边不等式


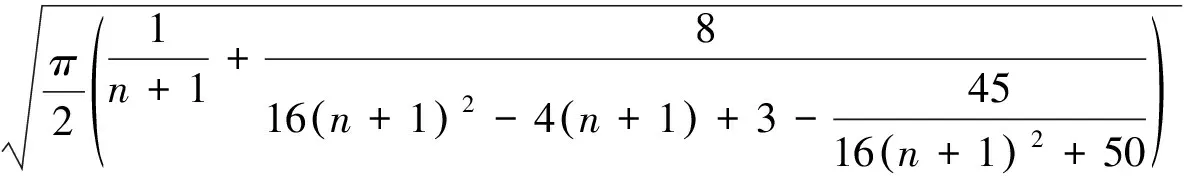
4 误差分析与计算


5 Wallis不等式
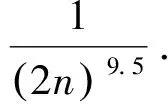

6 结 论

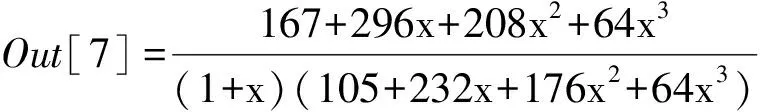
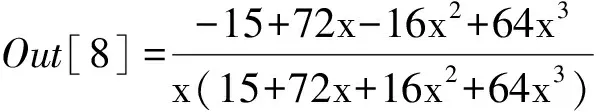

——酒泉晋城门

