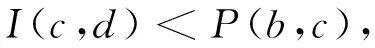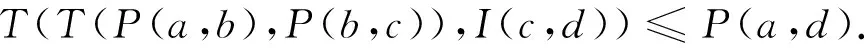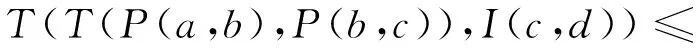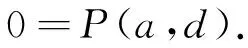严格偏好关系T-S-半传递性相关性质的研究*
刘雪琴, 武彩萍, 杨晓晨
(太原理工大学 数学学院,山西 太原 030024)
严格偏好关系T-S-半传递性相关性质的研究*
刘雪琴, 武彩萍, 杨晓晨
(太原理工大学 数学学院,山西 太原 030024)
摘要:基于可加的φ-模糊偏好结构,研究了严格偏好关系的T-S-半传递性相关性质.首先,给出了严格偏好关系的T-S-半传递性的一个充分条件; 其次,得出了P∘TP∘TI⊆P与(P∘TP)∩T(I∘TI)=Ø之间的一个等价命题; 最后,研究了(P∘TP)∩T(I∘TI)=Ø与S2条件之间的等价性.这些结论丰富了模糊偏好结构的研究.
关键词:可加的φ-模糊偏好结构; T-S-半传递性; 严格偏好关系; 关于Nφ旋转不变的t-模; 无零因子t-模
0引言
1971年,Chipman[1]首次提出“半传递性”概念. 关系Q满足半传递性是指对于论域A中的备择对象a,b,c,d,若a与b、b与c均具有关系Q,则或者a与d具有关系Q,或者d与c具有关系Q.关系的半传递性在生活生产中应用广泛,因此半传递性的研究是众多研究者关心的问题之一[2-5].由于实际问题的复杂性及人的主观性,精确的数据往往很难获取.1994年,Fodor[6]定义了模糊关系的T-S-半传递性.
模糊关系性质的研究对模糊偏好结构的研究至关重要.1978年,Orlovsky[7]已提出了模糊偏好构模理论.1997年,De Baets等[8]给出了可加的-模糊偏好结构的定义.由于该结构具有良好的性质,因而众多学者在该结构上进行了研究[9-11]. 2011年,Diaz等[11]在该模糊偏好结构下,首次研究了严格偏好关系的半传递性,在T为无零因子t-模下得到了一些结论. 2015年,刘等[12]在旋转不变的模下给出了严格偏好关系T-S-半传递性的必要条件. 鉴于此,本文给出严格偏好关系T-S-半传递性的充分条件,并进一步研究了严格偏好关系T-S-半传递性的相关性质.
1预备知识
首先给出自同构、t-模、t-余模、 非等模糊逻辑联结运算的定义.
定义 1[13]设φ:[a,b]→[a,b]是严格增的连续函数,若其满足φ(a)=a,φ(b)=b,则称φ为[a,b]上的一个自同构.
定义 2[14]设T:[0,1]×[0,1]→[0,1],若其满足:
1) 对称性: ∀x,y∈[0,1],T(x,y)=T(y,x);
2) 单调性: ∀x1≤x2,y1≤y2⟹T(x1,y1)≤T(x2,y2);
3) 结合律: ∀x,y,z∈[0,1],T(T(x,y),z)=T(x,T(y,z));
4) 边界条件: ∀x∈[0,1],T(1,x)=x,则称T是一个t-模.
设S:[0,1]×[0,1]→[0,1]满足对称性、 单调性、 结合律且满足: 4′) ∀x∈[0,1],S(0,x)=x,则称S是一个t-余模.
常见的t-模和t-余模有:
取小t-模:T(x,y)=x∧y,该t-模记为min或TM. 对∀T,TM≥T;
取大t-余模:S(x,y)=x∨y,该t-余模记为max.
Lukasiewiczt-模:T(x,y)=max(0,x+y-1),该t-模记为W;
Lukasiewiczt-余模:S(x,y)=min(1,x+y),该t-余模记为W′;

定义 3[13]设n:[0,1]→[0,1],若n单调减且满足n(0)=1,n(1)=0,则称n是一个模糊非,简称为非. 若n严格减且连续,则称n是一个严格非. 若一个严格非n满足复原律: ∀x∈[0,1],n(n(x))=x,则称n为一个强非.
例如:N(x)=1-x是强非,我们称之为标准非.
命题 1[13]N:[0,1]→[0,1]为强非,当且仅当存在[0,1]上的自同构φ使得
这里,用Nφ表示由φ生成的强非.
定义 4[13]设T,S分别为t-模和t-余模,n为强非,若T与S满足n-De Morgan律:n(S(x,y))=T(n(x),n(y))或n(T(x,y))=S(n(x),n(y)),则称(T,S,n)是De Morgan三元组.
定义 5[13-14]设T是一个t-模,
1) 若T对每个变量均左连续,则称T是左连续的;
2) 若∀x,y∈(0,1),T(x,y)≠0,则称T是无零因子t-模;
3) 若∀x,y,z∈[0,1],T(x,y)≤z⟺T(x,Nφ(z))≤Nφ(y),则称T是关于Nφ旋转不变的t-模.
如TM是无零因子t-模,W是关于标准非N旋转不变的左连续的t-模.

其次介绍模糊关系的有关定义以及相关结论.
定义 7[14]设T,S分别为t-模和t-余模,Q是A上的模糊关系.
1) 若∀a,b,c,d∈A,T(Q(a,b),Q(b,c))≤S(Q(a,d),Q(d,c)),则称Q满足T-S-半传递性.
2) 若∀a,b,c∈A,T(Q(a,b),Q(b,c))≤Q(a,c),则称Q满足T-传递性.
3) 若∀a,b∈A,T(Q(a,b),Q(b,a))=0,则称Q满足T-非对称.
特殊地,∀a,b∈A, Q(a,b)=0或Q(b,a)=0, 则称Q非对称.
4) 若∀a,b∈A, S(Q(a,b),Q(b,a))=1, 则称Q满足S-强完全.
特殊地,∀a,b∈A, Q(a,b)=1或Q(b,a)=1,则称Q强完全.
引理 1[10]若T关于Nφ满足旋转不变性,则∀x,y∈[0,1],有
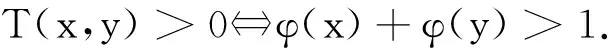
引理 2[15]若T关于Nφ旋转不变,则T是左连续的.
引理 3[14]设Q1,Q2,Q3是A上的模糊关系,若T左连续,则
引理 4[11]设Q是A上的模糊关系,T为无零因子t-模,若Q满足T-传递,则Q非对称.
引理 5[12]若T左连续,I是任意指标集,则∀ai∈[0,1](i∈I),有
注 1若T左连续,Q,Q1,Q2,Q3是A上模糊关系,则
2T-S-半传递性相关性质研究
本节首先介绍可加的φ-模糊偏好结构的定义以及文献中的相关结论,然后进一步讨论严格偏好关系的T-S-半传递性的相关性质.
下面给出了可加的φ-模糊偏好结构的定义及性质.
定义 8[8]设P,I,J是A上的模糊关系,若
1)I是自反,对称的;
2)


(1)



命题 2[16](P,I,J)是一个A上可加的φ-模糊偏好结构,则下列结论成立:
1)R强完全⟹J=Ø且P非对称.
2)J=⟹.
许多文献在可加φ-模糊偏好结构下研究了严格偏好关系的T-S-半传递性,并得出一些结论.
命题 3[11]设(P,I,J)是A上可加的φ-模糊偏好结构,若P满足P∘TP∘TI⊆P或I∘TP∘TP⊆P或P∘TI∘TP⊆P,则P是T-传递的.
命题 4[12]设(P,I,J)是A上可加的φ-模糊偏好结构,R强完全,T关于Nφ旋转不变,则下列说法等价:
1)P满足T-S-半传递;
2)R∘TP∘TP⊆P;
3)P∘TP∘TR⊆P.
命题 5[12]设(P,I,J)是A上可加的φ-模糊偏好结构,(T,S,Nφ)是De-Morgan三元组,且T关于Nφ旋转不变,考虑下列陈述:
1)P满足T-S-半传递性;
2)P∘TP∘TI⊆P;
3)I∘TP∘TP⊆P;
4)P∘TP∩TI∘TI=Ø;
5)S2条件: ∀a,b,c,d∈A,T(T(P(a,b),P(b,c)),I(b,d))≤S(Nφ(I(a,d)),Nφ(I(d,c))), 则1)⟹2)⟹4)⟹5); 1)⟹3)⟹4)⟹5).
注 3文献[12]中已举出反例说明命题5中结论不可逆.
由命题5,注3知,在普通情况下严格偏好关系的半传递性一些等价结论在模糊情况下已不再不成立.因此下面对严格偏好关系T-S-半传递性相关性质作进一步研究.
首先,给出了严格偏好关系的T-S-半传递性的一个充分条件.
命题 6设(P,I,J)是A上可加的φ-模糊偏好结构,R强完全,(T,S,Nφ)是De-Morgan三元组,T关于Nφ旋转不变,若P∘T(P∘TMI)⊆P,则P满足T-S-半传递性.
证明T关于Nφ旋转不变且R强完全,故由命题4只需证P∘TP∘TR⊆P.
由引理2及注1知: 要证P∘TP∘TR⊆P,即证∀a,b,c,d∈A,
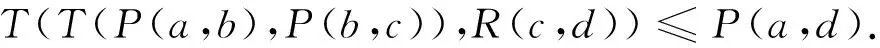
(2)
由P∘T(P∘TMI)⊆P,即对a,b,c,d∈A有
(3)
下面分1)和2)两种情况进行分类讨论.
1) 当I(c,d)≥P(b,c),则TM(P(b,c) 2) 当 (4) 则TM(P(b,c),I(c,d)=I(c,d), 式(3)即为 (5) 由R强完全得R(c,d)=1或R(d,c)=1. ① 若R(d,c)=1,则由命题2知:P(c,d)=0,所以I(c,d)=R(c,d), 则又由式(5)知 ② 若R(c,d)=1,则由命题2知:P(d,c)=0,故 (6) 故要证式(2)即证 (7) 若P(a,b)=0或P(b,c)=0,则显然式(7)成立. 下面设P(a,b)>0且P(b,c)>0,则由命题 2(1) 以及Q强完全知P非对称, 所以,P(c,b)=0且P(b,a)=0. 由P∘T(P∘TMI)⊆P知a,b,c,d∈A, (8) 下面分a)和b)两种情况进行分类讨论. a) 若P(c,d)≤I(d,a),此时TM(P(c,d),I(d,a))=P(c,d),式(8)即为T(P(b,c),P(c,d))≤0. 由T关于Nφ旋转不变得T(P(b,c),Nφ(0))≤Nφ(P(c,d)),即P(b,c)≤Nφ(P(c,d))=R(d,c). 又由式(6)知:P(b,c)≤I(c,d),与式(4)矛盾,故这种情况不存在. b) 若P(c,d)>I(d,a),则TM(P(c,d),I(d,a))=I(d,a). 故式(8)即为T(P(b,c),I(d,a))=0,由T关于Nφ旋转不变得:T(P(b,c),Nφ(0))=Nφ(I(d,a)),即P(b,c)≤Nφ(I(d,a))=φ-1(1-φ(I(d,a))). 又由式(1)知 (9) 由R强完全知R(a,d)=1或R(d,a)=1. b1) 若R(a,d)=1,则由命题2知:P(d,a)=0,式(9)即为φ(P(b,c))≤φ(P(a,d)),故 (10) 由于TM是最大的t-模及P∘T(P∘TMI)⊆P,故对于任意的关于Nφ旋转不变的t-模均有 由引理2,引理3知:P∘TP∘TI=P∘T(P∘TI)⊆P. 由命题3知P满足T-传递性,故对a,b,c∈A,T(P(a,b),P(b,c))≤P(b,c). 又由式(10)知:T(P(a,b),P(b,c))≤P(b,c)≤P(a,d),即式 (7)成立. b2) 若R(d,a)=1,则由命题2知:P(a,d)=0. 式(9)即为φ(P(b,c))≤φ(P(d,a)),故 (11) (反证)若式(7)不成立,即T(P(a,b),P(b,c))>P(a,d)=0, 则由P满足T-传递性知: 对a,b,d∈A,P(d,b)≥T(P(d,a),P(a,b)), 又由式(11) 得,P(d,b)≥T(P(d,a),P(a,b))≥T(P(b,c),P(a,b))>P(a,d)=0, 即 (12) 又由式(4)且R(c,d)=1及φ(R(c,d))=φ(P(c,d))+φ(I(c,d)) 知 故由引理1及P的T-传递性知b,c,d∈A,P(c,d)≥T(P(b,c),P(c,d))>0. 故P(b,d)>0. 由P的非对称性知P(d,b)=0与式(12)矛盾. 所以假设不成立,即式(7)成立. 综上:P满足T-S-半传递性. 下面我们通过两个例子来说明条件P∘T(P∘TMI)⊆P确实是P满足T-S-半传递性的充分条件,但不是必要条件. 例 1设A={a,b,c,d},定义A上的模糊关系P,I,J为 当φ(x)=x时,容易验证(P,I,J)是A上可加的φ-模糊偏好结构,且R强完全. 令T=W,显而易见, 且 由命题4知:P满足T-S-半传递性. 例1说明若条件P∘T(P∘TMI)⊆P成立,则P满足T-S-半传递性. 例 2设A={a,b,c,d},定义A上的模糊关系P,I,J为 当φ(x)=x时,容易验证(P,I,J)是A上可加的φ-模糊偏好结构,且R强完全. 令T=W,显而易见, 然而, 由命题4知:P满足T-S-半传递性. 例2说明即使不满足条件P∘T(P∘TMI)⊆P,P也有可能满足T-S-半传递性. 其次,研究P∘TP∘TI⊆P与P∘TP∩TI∘TI=Ø之间的等价性. 命题 7设(P,I,J)是A上可加的φ-模糊偏好结构,R强完全,T关于Nφ旋转不变,T1为无零因子t-模,若P满足T-传递且P∘T1P∩T1I∘T1I=Ø,则P∘TP∘TI⊆P. 证明由引理2及注1知: 要证P∘TP∘TI⊆P,即证 (13) 1) 若P(a,b)=0或P(b,c)=0,则T(T(P(a,b),P(b,c)),I(c,d))=0≤P(a,d),即式(13)成立. 2) 若P(a,b)>0且P(b,c)>0,所以T1(P(a,b),P(b,c))>0.由P∘T1P∩T1I∘T1I=Ø,即对a,b,c,d∈A有 又T1(P(a,b),P(b,c))>0,所以T1(I(a,d),I(d,c))=0,所以I(a,d)=0或I(d,c)=0. a) 若I(d,c)=0,由I的自反性得I=(c,d)=0. 所以T(T(P(a,b),P(b,c),I(c,d))=0≤P(a,d),即式(13)成立. b) 若I(a,d)=0,由命题2知:P非对称. 所以P(a,d)=0或P(d,a)=0. 若P(d,a)=0,则又由式(1)知:P(a,d)=1,则显然T(T(P(a,b),P(b,c)),I(c,d))≤1=P(a,d),即式(13)成立. 若P(a,d)=0,则又由式(1)知:P(d,a)=1,由P满足T-传递得:P(d,c)≥T(P(d,a),P(a,c))=T(1,P(a,c))=P(a,c), 即 (14) 又由式(1)知: 对c,d∈A,φ(P(d,c))+φ(I(c,d)))≤1,即φ(P(d,c))≤1-φ(I(c,d)). 由φ是[0,1]上的自同构得:P(d,c)≤φ-1(1-φ(I(c,d)))=Nφ(I(c,d)), 即T(P(d,c),1)≤Nφ(I(c,d)). 故由T关于Nφ旋转不变得 (15) 由式(14)和式(15)知 故式(13)成立. 由命题3,命题5及命题7易得下面的定理. 定理 1设(P,I,J)是A上可加的φ-模糊偏好结构,R强完全,T关于Nφ旋转不变,T1为无零因子t-模,且T1≤T,则下列说法等价: 1)P满足T-传递且P∘T1P∩T1I∘T1I=Ø, 2)P∘TP∘TI⊆P. 最后,研究S2条件与P∘TP∩TI∘TI=Ø之间的等价性. 命题 8设(P,I)是A上可加的φ-模糊偏好结构,T1为无零因子t-模,P∘T1I∘T1P⊆P,若T关于Nφ旋转不变且S2条件成立,则P∘TP∩TI∘TI=Ø. 证明由引理2及注1知: 要证P∘TP∩TI∘TI=Ø,即证 (16) 1) 若P(a,b)=0或P(b,c)=0,则T(T(P(a,b),P(b,c)),T(I(a,d),I(d,c)))=0,即式(16)成立. 2) 若P(a,b)>0且P(b,c)>0,则T1(P(a,b),P(b,c))>0. 由P∘T1I∘T1P⊆P及命题3知:P是T1-传递. 对a,b,c∈A,P(a,c)≥T1(P(a,b),P(b,c))>0,由引理4知:P非对称,故 (17) 由P∘T1I∘T1P⊆P即对a,b,d∈A有0=P(a,a)≥T1(T1(P(a,b),I(b,d)),P(d,a)). 因P(a,b)>0且P(b,c)>0知P(a,c)=1. 又由式(1)及式(17)知 (18) 由P∘T1I∘T1P⊆P即对a,b,d∈A有0=P(a,a)≥T1(T1(P(a,b),I(b,d),P(d,a)). 因P(a,b)>0,所以I(b,d)=0或P(b,d)=0. ① 当I(b,d)=0,由P非对称及式(1)得P(b,d)=1 或P(d,b)=1. A) 若P(b,d)=1,由P是T1-传递得:P(a,b)=T1(P(a,b),P(b,d))≤P(a,d),即 (19) 又由式(1)知:φ(P(a,d))+φ(I(a,d)))≤1,即P(a,d)=T(P(a,d),1)≤Nφ(I(a,d)). 故由T关于Nφ旋转不变得 (20) 由式(19),式(20)及t-模的结合对称性有 故式(16)成立. B) 若P(d,b)=1,由P∘T1I∘T1P⊆P即对b,c,d∈A有0=P(b,b)≥T1(T1(P(b,c),I(c,d)),P(d,b)). 由P(d,b)=1及P(b,c)>0得I(c,d)=0. 又由I的对称性得I(d,c)=0. 故T(T(P(a,b),P(b,c)),T(I(a,d),I(d,c)))=T(T(P(a,b),P(b,c)),T(I(a,d),0))=0. 故式(16)成立. ② 当P(b,d)=0,由P∘T1I∘T1P⊆P即对a,c,d∈A有0=P(c,c)≥T1(T1(P(c,d),I(d,a)),P(a,c)). 又由式(18)得:I(a,d)=0或P(c,d)=0. A) 若I(a,d)=0,T(T(P(a,b),P(b,c)),T(I(a,d),I(d,c)))=T(T(P(a,b),P(b,c)),T(0,I(d,c)))=0. 即式(16)成立. B) 若P(c,d)=0,由P∘T1I∘T1P⊆P即对a,b,d∈A, 0=P(b,b)=T1(T1(P(b,d),I(d,a)),P(a,b)). 由P(a,b)>0得I(d,a)=0或P(b,d)=0. a) 若I(d,a)=0,由I的对称性I(a,d)=0. 故T(T(P(a,b),P(b,c)),T(I(a,d),I(d,c)))=T(T(P(a,b),P(b,c)),T(0,I(d,c)))=0. 故式(16)成立. b) 若 (21) 由P∘T1I∘T1P⊆P即对b,c,d∈A有P(b,b)≥T1(T1(P(b,c),I(c,d)),P(d,b)).又P(b,c)>0 得I(c,d)=0或P(d,b)=0. b1) 若I(c,d)=0,由I的对称性I(d,c)=0. 得 (22) 即式(16)成立. b2) 若P(d,b)=0,则由式(1)及式(21)知:I(b,d)=1,S2条件成立得 由T关于Nφ旋转不变得 即式(16)成立. 由命题5和命题8易得下面的定理. 定理 2设(P,I)是A上可加的φ-模糊偏好结构,T1为无零因子t-模,P∘T1I∘T1P⊆P,若T关于Nφ满足旋转不变性,则下列说法等价: 1)P∘TP∩TI∘TI=Ø, 2)S2条件成立. 3结束语 我们知道,在普通情况下,严格偏好关系的半传递性、P∘P∘I⊆P以及(P∘P)∩(I∘I)=Ø是等价的,但是由命题5可以看出,在模糊情况下这些等价性已不再成立.其中,严格偏好关系的T-S-半传递性强于P∘TP∘TI∩P,P∘TP∘TI∩P强于(P∘TP)∩T(I∘TI)=Ø, (P∘TP)∩T(I∘TI)=Ø强于S2条件.有鉴于此,本文首先给出严格偏好关系的T-S-半传递性的一个充分条件(命题6); 其次对P∘TP∘TI⊆P进行了研究,给出了它的一个充分条件(命题7),并且得到了它与(P∘TP)∩T(I∘TI)=Ø之间的关系(命题8,定理1); 最后研究了(P∘TP)∩T(I∘TI)=Ø与S2条件之间的等价性(定理2). 从本文的研究中得到P∘T(P∘TMI)⊆P是严格偏好关系的T-S-半传递性的一个充分条件,那么,I∘TMP∘TP⊆P是否也是严格偏好关系的T-S-半传递性的充分条件还有待进一步研究. 参考文献: [1]Chipman J. Consumption theory without transitive indifference, in Preferences, Utility and Demand[M]. New York: Harcourt Brace, 1971. [2]Luce R. Semi-orders and a theory of utility discrimination[J]. Econometrica, 1956, 24: 178-191. [3]Roubens M, Vincke Ph. Preference modelling[M]. Berlin: Springer-Verlag, 1985. [4]Monjardet B. Axìonatiques et propriétés des quasi-orders[J]. Math. Sci. Hum., 1978, 63: 51-82. [5]Pirlot M, Vincke P. Semi-order: properties, representations, applications[M]. Dordrecht/Boston/London: Kluwer Academic Publishers, 1997. [6]Fodor J, Roubens M. Fuzzy preference modeling and multicriteria decision support[M]. Dordrecht/Boston/London: Kluwer Academic Publishers, 1994. [7]Orlovskys A. Decision making with a fuzzy preference relation[J]. Fuzzy Sets and Systems, 1978(l): 155-167. [8]De Baets B, Van de Walle B. Minimal definitions of classical and fuzzy preference structures[C]. New York: Proceeding of the Annual Meeting of the North American Fuzzy Information Processing Society, 1997: 299-304. [9]Bufardi A. An alternative definition for fuzzy interval orders[J]. Fuzzy Sets Systems, 2003, 133: 249-259. [10]Díaz S, De Baets B, Montes S. On the Ferrers property of valued interval orders[J]. TOP, 2011, 19: 421-447. [11]Díaz S, Induráin E, De Baets B, Montes S. Fuzzy semi-orders: The case of t-norms without zero divisors[J]. Fuzzy Sets and Systems, 2011, 184: 52-67. [12]刘雪琴, 武彩萍, 王绪柱. 基于旋转不变模的T-S-半传递性的研究[J]. 模糊系统与数学, 2015(4): 1-10. Liu Xueqin, Wu Caiping, Wang Xuzhu. A study onT-S-semitransitivity based on the rotation invariantt-norms[J]. Fuzzy systems and mathematics, 2015(4): 1-10. (in Chinese) [13]Klement E, Mesiar R, Pap E. Triangular norms[M]. Dordrecht: Kluwer Academic Publishers, 2000. [14]Fodor J, Roubens M. Fuzzy preference modeling and multicriteria decision support[M]. Dordrecht/Boston/London: Kluwer Academic Publishers, 1994. [15]Jenei S. Geometry of left-continuous t-norms with strong induced negation[J]. Belg. J. Oper. Res. Statist Comput. Sci., 1998, 38: 5-16. [16]仝坤玉, 王绪柱.T-S-Ferrers性质与区间序指标[J]. 模糊系统与数学, 2014, 28: 144-151. Tong Kunyu, Wang Xuzhu.T-S-Ferrers property and interval order indicators[J]. Fuzzy Systems and Mathematics, 2014, 28: 144-151. (in Chinese) Study on theT-S-Semitransitivity Properties of Strict Preference Relation LIU Xue-qin, WU Cai-ping,YANG Xiao-chen (College of Mathematics, Taiyuan University of Technology, Taiyuan 030024, China) Abstract:Based on additive φ-fuzzy preference structures, the T-S-Semi-transitivity properties of the strict preference relation was studied. Firstly, a sufficient condition of the T-S-Semi-transitivity of the strict preference relation was given. Secondly, an equivalent conclusion between P∘TP∘TI⊆P and (P∘TP)∩T(I∘TI)=Ø was presented. Finally, the equivalence between (P∘TP)∩T(I∘TI)=Ø and the condition S2 was investigated. The results enrich the research of the fuzzy preference structures. Key words:additive φ-fuzzy preference structure; T-S-Semitransitivity; strict preference relation; rotation invariance t-norm; t-norm without zero divisor 文章编号:1673-3193(2016)02-0097-07 *收稿日期:2015-07-15 基金项目:山西省自然科学基金资助项目(2013011004-1); 山西省留学回国人员科研资助项目(2013052); 山西省研究生教育改革研究课题(20142028) 作者简介:刘雪琴(1989-),女,硕士生,主要从事模糊偏好研究.通信作者: 武彩萍(1967-),女,副教授,硕士,主要从事模糊决策的研究. 中图分类号:O159 文献标识码:A doi:10.3969/j.issn.1673-3193.2016.02.001