基于BP、 PCA-BP和PLS算法对城市降水量的预测研究*

牛志娟，胡红萍，白艳萍，李　强

(1. 中北大学 理学院，山西 太原 030051； 2. 中北大学 计算机与控制工程学院，山西 太原 030051)



基于BP、 PCA-BP和PLS算法对城市降水量的预测研究*

牛志娟1，胡红萍1，白艳萍1，李强2

(1. 中北大学 理学院，山西 太原 030051； 2. 中北大学 计算机与控制工程学院，山西 太原 030051)

摘要:降水量预报对农业生产、 城市经济和防控城市内涝等具有重要意义. 本文应用BP神经网络、 基于主成分分析的BP神经网络和偏最小二乘(PLS)算法建立了三种降水量预测模型. 通过比较三种模型的MSE和MAE值，发现PLS模型的预测能力优于其它两种模型. 在PLS模型中，采用PLS算法所提取主成分的因变量总方差比例为0.899，这就说明模型具有很好的稳定性和预测能力. 通过对PLS模型进行分析，发现极端最低气温(X1)、 极端最高气温(X2)、 降水距平百分率(X3)、 平均气温(X4)是影响城市降水量的主要因素，且降水量随着X1、 X2、 X3、 X4的增大而增大.

关键词:偏最小二乘算法； BP神经网络； 降水量预测； PCA-BP神经网络

降水量指一定时间内降落到水面上未经渗漏、 流失、 蒸发而累积起来的水的深度，是衡量一个地区降水多少的数据. 进入汛期以来，在厄尔尼诺现象的影响下，多个城市降水量达到或突破了历史极值，出现小区被淹、 道路积水、 交通阻滞、 居民受困等现象，导致城市内涝防控“雪上加霜”. 城市降水量预测是目前被全世界普遍关注的问题之一[1]. 降水量是水文和水力系统中的重要输入数据，对国民经济特别是农业生产影响极大. 因此，对城市降水量进行准确性预测为当地农业、 水利等政府智能部门防治旱涝灾害的有效手段[2].

降水量预测对农业生产、 城市经济、 防控城市内涝等具有极其重要的作用. 近年来，降水量的预测受到了广泛关注[3]. 常用的预测流域降雨量和水文气象的方法包括： 人工神经网络(Artificial Neural Network，ANN)[4]、 混沌贝叶斯[5]等. 其中，ANN算法逼近复杂的非线性关系，被广泛用于气象、 水资源等预测. 然而，由于ANN是一种分布式并行信息处理的算法模型，得到的非线性系统是一个黑箱，难以对各项性能指标的机理进行解释. 偏最小二乘(Partial Least Square，PLS)算法计算量小、 预测精度较高、 所构造的潜变量较确定、 易于定性解释，能够在自变量存在严重相关性的条件下进行回归建模. 迄今为止，基于PLS算法对城市降水量预测的研究甚少. 由于降水量的变化过程通常是动态的、 复杂的非线性问题，其准确性很难预测，因此，准确提取影响降水量主要因素之间的相关信息是当前研究的热点问题，对如何开发有效的多变量降水量预测模型具有重要的意义.

本文以张北市2009年月降水为因变量，以影响城市降水量的结构与预测精度的指标为自变量，分别采用ANN、 PCA-BP和PLS算法建立了降水量预测模型，为城市降水量的精确预测提供一种较好的方法，进而探讨了影响城市降水量的主要因素.

1预测模型方法

1.1BP神经网络

BP神经网络(BP Neural Network)是一种反向传播算法的非线性动态信息处理系统网络，是目前气象应用最广泛的网络模型之一[6]. 拓扑结构如图 1 所示.

图 1 中，X1，X2，…，Xn是网络输入值，Y1，Y2，…，Yn是网络预测值，ωij和ωjk为网络的权值. 当网络输入节点为n、 输出节点数为m时，BP神经网络表示从n个自变量到m个因变量的函数影射关系. 本文建立的基于主成分分析的BP神经网络模型采用的是一个3层的前馈网络模型，其模型计算的输出为

(1)

式中：bi为输入层到隐含层之间的激活函数值；ωij是连接权值；rj为输出层阈值. 其中f(x)采用Sigmoid函数

(2)

图 1　BP神经网络拓扑结构图Fig.1　The topology structure of BP neural network

1.2 PCA-BP神经网络

本文选取张北市1989～2008年间极端最低气温(X1)、 极端最高气温(X2)、 降水距平百分率(X3)、 降水量(X4)、 平均气温距平(X5)、 平均最低气温(X6)等6个因子的数据作为网络的学习训练样本，以2009年12个月的降水量为预测对象，通过提取影响降水量各指标中主成分，建立基于主成分分析的BP神经网络预测模型. 由于PCA-BP模型的不稳定性，每次的预测结果都有所不同. 所以本文采用均方误差(MSE)和平均绝对误差(MAE)两种统计评价指标来比较不同主成分个数的PCA-BP模型预测精度，两种评价指标的计算如式(3)，式(4)所示.

(3)

(4)

1.3偏最小二乘(PLS)算法

(5)

式中：n为所建立的模型中训练集的个数；A是PLS主成分个数.

本文以1956-2008年的降水量数据分别建立了BP、 PCA-BP和PLS模型，然后对2009年降水量数据进行预测. 采用一个简单的三层BP神经网络将影响降水量6个因素的数据作为网络输入，以Sigmoid函数作为网络的激活函数，2009年降水量作为网络的输出建立预测模型. 由于BP算法采用的是梯度下降法，故训练过程中易出现局部极小值.

主成分分析(Principal Component Analysis)是一种通过降维技术把多个变量化为少数几个主成分的多元统计方法[8]. 文中将主成分分析和BP神经网络相结合(PCA-BP)，提取2个主成分，累计贡献率达到97%，PCA-BP的主要思想是通过解决数据多的非线性问题来克服输入数据的冗余性，进而使得预测精度较高于传统的BP神经网络.

偏最小二乘法在一定程度上解决了小样本和多因变量问题，是主成分分析、 典型相关分析和多元线性回归的有机结合. PLS回归类似于主成分分析，不同的是目标函数不一样，两者都是用提取成分的办法来提炼主要信息，从而减少变量.

2结果与讨论

2.1BP-ANN模型预测结果

采用MATLAB(2014版)软件对张北市降水量预测模型进行分析. 为提高网络的学习收敛速度，首先对原始数据进行归一化处理，归一化公式为

(6)

选取1956～2008年的数据集作为训练集，以2009年的降水量数据作为测试的独立样本. 在BP网络训练过程中，将训练集作为BP神经网络的输入，设定网络的目标误差为0.1，训练次数10 000次，学习速率为0.75，BP网络中隐含层和输出层的神经元函数选用S型正切函数tansing，网络的训练函数为traing. 建立了张北市降水量BP网络预测模型，预测结果如图 2. 由图 2 可知，四、 七、 八、 九月份的误差较大，四月份的相对误差达到170，其它八个月份的预测值基本趋于实际值，预测效果基本稳定. 一月、 十一月份的相对误差与实际值的误差最小，其预测精度优于其它月份.

图 2　采用BP模型对2009年张北市降水量的预测结果Fig.2　The forecast results of Zhangbei city precipitation in 2009 according to BP neural network

2.2PCA-BP模型预测结果

采用MATLAB (2014版)软件分析，通过计算主成分分析特征值的累积贡献率来确定网络样本输入，建立了基于主成分分析的BP神经网络(PCA-BP)预测模型. 通过主成分分析，得到影响月平均温度的6个相关系数矩阵的特征值及贡献率. 如表 1 所示，前两个主成分解释了原来6个因子97%的信息. 通常情况下，当因子累积贡献率达到90%时，就能较好地反映相关因子的影响，因此，前2个成分反映了原始6个变量的大部分信息.

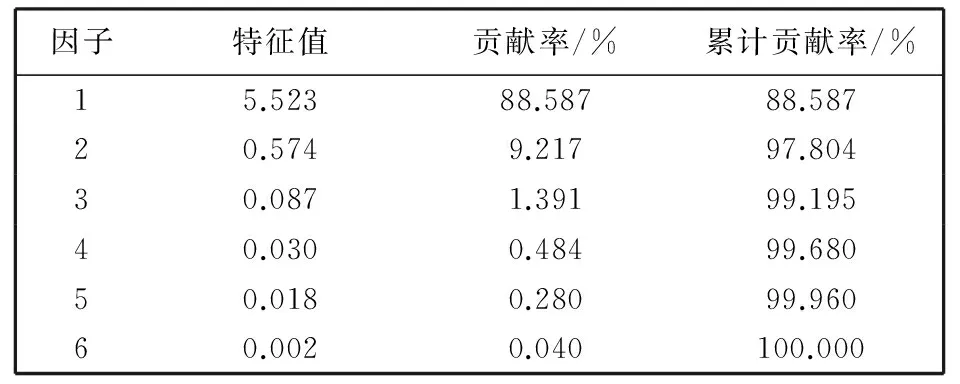
表 1　基于主成分的BP神经网络的2009年张北市降水量分析结果

本文选取2个主成分个数进行预测，其预测结果如图3所示，由图3可以看出，五月、六月、九月份的误差较大，其它9个月的实际值和预测值趋于吻合，预测精度优于原始的BP-ANN模型.

图 3　PCA-BP模型对2009年张北市降水量的预测结果Fig.3　The forecast results of Zhangbei city precipitation in 2009 according to PCA-BP neural network

2.3PLS模型预测结果

本文以2009年张北市降水量为因变量Y，以极端最低气温(X1)、 极端最高气温(X2)、 降水距平百分率(X3)、 平均气温(X4)、 平均距平(X5)、 平均最低气温(X6)等6项指标为自变量构建张北市降水量PLS预测模型(1). 模型(1)结果显示如表 2. 由结果可知，选取了各因子之间的结构参数，确定各因子之间关系，并对张北市月降水量的模型进行预测分析. 该模型的性质参数和结构参数如表 2.

表 2　张北市2009年月降水量预测结果

PLS模型中各自变量的VIP(Variable Importance in the Projection)值列于表 3 中，根据准回归系数前的正负号，可以判断各自变量对因变量影响的性质. 应用PLS 算法得到表3中各自变量的准回归系数和常数项建立的降水量模型，得到的多变量方程为

LogY=1.906+0.229X1+0.199X2+

(7)

表 3　模型(1)中各参数的VIP值和准回归系数Tab.3　The VIP and the regression coefficient of parameters in model(1)

表 4　模型(1)的结果分析

在建立的PLS模型中，影响LogY的主要因素是X1(极端最低气温)、X2(极端最高气温)、X3(降水距平百分率)和X4(平均气温). 由式(5)中准回归系数的正负可以判断各个自变量对因变量的影响，PLS的LogY值随着X1、X2、X3、X4的增大而增大.

2.4 三种模型结果比较

综上所述，影响城市降水量的主要因素有极端最低气温(X1)、 极端最高气温(X2)、 降水距平百分率(X3)、 平均气温(X4)等4个因素，降水量随着X1、X2、X3、X4的增大而增大，降水距平百分率也随之增大.

采用均方误差(MSE)和平均绝对误差(MAE)两种统计评价指标来评价BP、 PCA-BP、 PLS模型的预测精度. 计算结果列于表 5，由表 5 可以看出BP模型的均方误差达到73.40，平均相对误差为49.41，是三种模型中误差最大的； PLS模型的均方误差为16.60，平均绝对误差12.44，是三种模型中误差最小的. 因此，PLS模型的预测效果优于BP、 PCA-BP模型.

表 5　BP、 PCA-BP 、 PLS 三种不同模型的均方误差和平均绝对误差

根据BP、 PCA-BP、 PLS三种模型的相对误差值，采用Excel(2003)绘图软件画出了BP、 PCA-BP、 PLS三种模型的预测误差对比图，如图 4 所示.

图 4　BP、 PCA-BP、 PLS模型对2009年张北市降水量的预测误差Fig.4　Prediction error of BP，PCA-BP and PLS models for precipitation of Zhangbei city in 2009

由图 4 可知，从三种模型相对降水量预测的稳定性和预测精度来讲，PLS模型都优于BP、 PCA-BP两模型. 从整体来看，四月、 七月的降水量较多，十一月、 十二月是降水量最少的两个月份，六月、 七月、 九月是PLS预测模型误差较大的三个月.

3结论

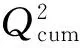
参考文献:

[1]周国良，张建云. 厄尔尼诺现象及其对我国水文气候的重大影响[J]. 水文，2002，22(3)： 14-17.

Zhou Guoliang，Zhang Jianyun. EI Nino and its effects on the climate in China[J]. Hydrology，2002，22(3)： 14-17. (in Chinese)

[2]白玉洁. 改进时间序列模型在降水量预测中的应用研究[J]. 计算机仿真，2011, 28(10)： 141-145.

Bai Yujie. Application of rainfall base on improved time series model[J]. Computer Simulation, 2011, 28(10): 141-145. (in Chinese)

[3]刘莉，叶文. 基于BP神经网络时间序列模型的降水量预测[J]. 水资源与水工程学报，2010，21(5)： 156-159.

Liu Li，Ye Wen. Precipitation prediction of time series model based on BP artificial neural network[J]. Journal of water Resources & water Engineering，2010，21(5)： 156-159. (in Chinese)

[4]谷晓平，王长耀，袁淑杰. GA-BP神经网络模型在流域面雨量预报的应用研究[J]. 热带气象学报，2006，22(3)： 248-252.

Gu Xiaoping，Wang Changyao，Yuan Shujie. GA-BP ANN model for river catchment precipitation forecast[J]. Journal of Tropical Meteorology，2006，22(3)： 248-252. (in Chinese)

[5]Bańbura M，Giannone D，Reichlin L，et al. Large Bayesian vector auto regressions[J]. Journal of Applied Econometrics，2010，25(1)： 71-92.

[6]葛彩莲，蔡焕杰，王健，等. 基于BP神经网络的降雨量预测研究[J]. 节水灌溉，2010(11)： 7-10.

Ge Cailian, Cai Huanjie, Wang Jian, et al. Study on rainfall forecast based on BP neural network[J]. Water Saving Irrigation，2010(11)： 7-10. (in Chinese)

[7]Wold S, Sjöström M, Eriksson L. PLS-regression： a basic tool of chemometrics[J]. Chemom. Intell. Lab. Syst. ，2001，58： 109-130.

[8]谢中华. MATLAB统计分析与应用： 40个案例分析[M]. 北京： 北京航空航天大学出版社，2010.

[9]Chen Jingwen，Peijnenburg WJGM and Quan Xie，et al. Is it possible to develop a QSPR model for directphotolysis half-lives of PAHS under irradiation of sunlight[J]. Environmental Pollution，2001，115： 137- 143.

[10]Niu Junfeng, Yu Gang, Schramm K W. Quantitative structure-property relationships on direct photolysis of PCDD/Fs on surfaces of flyash[J]. SAR & QSAR in Environmental Research , 2004，18(4)： 265-277.

Prediction of Urban Precipitation Based on Algorithms of BP，PCA-BP and PLS

NIU Zhi-juan1，HU Hong-ping1，BAI Yan-ping1, LI Qiang2

(1. School of Science，North University of China，Taiyuan 030051，China；2. School of Computer Scince and Control Engineering, North University of China, Taiyuan 030051, China)

Abstract:The precipitation forecast has important meaning to agricultural production，city economy and city water logging prevention and control etc. In this paper, three kinds of models are established. These models are BP neural network, partial least squares (PLS) algorithm and BP neural network based on principal component analysis(PCA-BP) respectely. By comparing the mean square error and the mean absolute error of the three models，we know that the stability and prediction ability of PLS model are better than the two others’. In PLS model, the total variance ratio of principal component is 0.899, which indicates that the model has well predictive ability. Through analysis of PLS model, it is shown that the main factors that affect urban precipitation are extreme minimum temperature (X1)，extreme maximum temperature (X2)，precipitation anomaly percentage (X3)，average temperature (X4) . Furthermore, the precipitation will increase with the increasing of (X1)，(X2)，(X3) and (X4).

Key words:partial least squares (PLS); BP neural network; prediction of precipitation; PCA-BP neural network

文章编号:1673-3193(2016)02-0181-06

*收稿日期:2015-10-01

基金项目：国家自然科学基金资助项目(61275120)

作者简介：牛志娟(1988-)，女，硕士生，主要从事神经网络预测方面的研究.通信作者： 胡红萍(1973-)，女，副教授 ，博士，主要从事工程中数学问题的研究.

中图分类号:O29

文献标识码:A

doi:10.3969/j.issn.1673-3193.2016.02.016