在问题导向型课堂中培养数学建模核心素养

万玥

【关键词】初中数学;问题导向型;数学建模;核心素养

在新课程改革下，初中数学以培养学生的数学学习能力为目标，重视学生逻辑能力与创新意识的培养，发挥学生的主体作用，数学建模能力的培养也引起了教师的重视。

一、问题导向教学法与数学建模结合的意义

问题导向法是一种教师在教学中将引导性问题提出并鼓励学生解决的一种教学模式，具有高效性、精简性、引导性的特点。教师在教学过程中采用问题导向法进行教学，设置与知识点相关的精简问题，通过一层层的难度与深度的提升，启发学生对相关知识点深入思考，引导学生自主学习，并对数学相关知识进行归纳完善，建立新旧知识间的联系，构建知识框架，提高学生数学思维能力。

数学建模是指在对实际问题进行分析和观察的基础上，利用现有各种数学知识，将实际问题转化为数学问题，提炼出数学模型进行解决的思路和方法。培养学生用数学建模解决实际问题的能力关键是把实际问题转化成数学问题，因此，问题导向教学法与数学建模相结合具有重要意义。

二、数学建模的课例分析

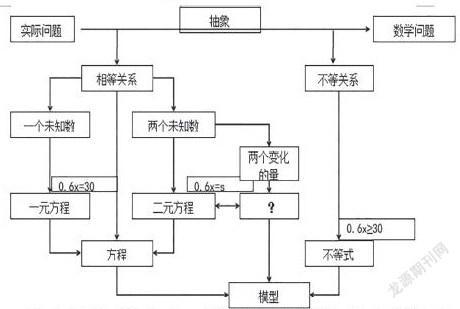
初中数学教学中的常用数学模型主要分四种，分别是方程（组）模型、不等式（组）模型、函数模型与几何模型。其中，方程（组）模型、不等式（组）模型、函数模型分别是表示数量的相等关系、不等关系、变化关系的数学模型。方程学生在小学就学过，而函数模型较为抽象。函数模型需要研究不同变量直接的对应关系与变化规律，通过分析自变量和因变量建立对应的关系式，从而把实际问题转化成函数问题。因此，函数概念的学习在初中数学教学过程中处于承上启下的位置，对于函数概念的教授举足轻重。下面将以八上《6.1函数》为例，具体阐述怎样用问题导向法渗透数学建模的思想。

问题导向型课堂常在新课引入过程依托现实问题创设情境，结合学生的已有经验基础，设计层次性与导向性的问题。而创设情境是课堂生活化的途径，是学生初步感受新知，导入课堂内容的重要环节，因此，导向性问题的设置是是激活学生思维，激发学生兴趣的重要环节。

（一）创设情境，初步感受

问题导向教学法最核心的问题，就是数学问题的提出首先要建立在对数学知识点的完整掌握并且全部理解的基础之上，只有这样才可以有针对性地提出问题。

笔者设置了师生游园的生活情境：上周我们学校组织了“梅韵寻踪”的社会实践活动，师生乘坐大巴车从学校去往梅园。然后根据学生的知识基础设置了三个导向性问题引导学生建立模型分析问题，让学生初步感受函数中的变量关系：

问题1：已知学校到梅园的路程为30km，大巴车行驶了0.6小时，大巴车的平均速度是多少？

问题2：已知学校到梅园的路程为30km，如果大巴车要在0.6h内到达梅园，大巴车的平均速度至少是多少？

问题3：已知大巴车的平均速度是50km/h。大巴车的行驶时间与路程是多少呢？

在问题1中，学生能够根据初一学习方程的经验基础，从题目中的“路程”“0.6小时”“平均速度”等关键词分析出本题是一道行程类问题，联想到“路程=速度×时间”的等量关系，从而设大巴车的平均速度为x km/h，建立关于x的一元一次方程模型（0.6x=30）。

问题2在问题1 的基础上发生了变化，题目问题从“大巴车行驶了0.6小时，大巴车的平均速度是多少”转变成了“大巴车要在0.6h内到达梅园，大巴车的平均速度至少是多少”，学生能够分析出“路程≥速度×时间”的不等关系，建立关于x的不等式模型（0.6x≥30）。

问题3则是去除了关于时间的条件，让学生直接求“大巴车的行驶时间与路程”。在这道题当中，根据“路程=速度×时间”的等量关系，学生设了时间为t h，路程为s km，建立了关于s，t的二元一次方程模型（s=200t）。并且，根据二元一次方程的学习内容，学生能够回答出“本题不能求出具体的时间与路程，因为速度50km/h没有变化，但是时间t，路程s都在变化。”

学生在坐大巴车去梅园的情境下，根据条件的不同，依次建立了不同模型“一元一次方程——不等式——二元一次方程”解决问题，让学生复习了初中学习的主要模型类型，为新课的讲授建立了知识框架，渗透了数学建模的核心素养。并且，教师设置阶梯问题，通过问题引导学生探究思考的过程。并且教师在引导学生探究过程中，适当地使用“启发讨论模式”“自学辅导模式”等教学方法增加课堂的趣味性，能够极大地提高学生的参与程度，激发学生探究的兴趣，增强学生的学习主动性，推动课堂教学的发展。

（二）复习回顾，引入新知

函数模型的学习强化了学生对对数学模型的认识和理解，为了确保教学设计更加系统全面，笔者设置了知识导图，借助知识导图帮助学生建立数学模型的框架，构建知识的联系，引导学生对于两个变化的量之间的关系的探究，培养学生良好的数学思维习惯和质疑探索的意识。

（三）合作探究，感受新知

学生是学习的主体，是教学过程中学习知识的接受者，老师要引导学生自主学习的能力，培养举一反三的习惯，学会发掘问题背后的连贯性的知识。因此笔者设置了三组探究活动，让学生合作交流，探讨分析。

探究活动一是某班学生的体检身高登记表，簡洁明了地表述出了学生学号与学生身高这两个量之间的关系，通过三个问题引导学生思考：

（1）3号、17号、21号学生的身高是多少？

随着学号x的变化，身高h变化吗？

当学号x取定一个确定的值时，对应身高h的取值是否唯一确定？（答：当学号x取定一个确定值时，对应身高h的取值也“唯一”确定。）

通过这三个层层递进的问题，让学生初步感受两个量的变化，在问题的引导下发现两个变量间一一对应的关系。

教师引导学生分析讨论，解决了探究活动一中的问题后，教师创设某城市的气温变化与搭小鱼的情境，让学生仿照探究活动一，提出问题后分组讨论，小组成员互相帮助，共同分析出变量间的关系。在这三个探究活动中，学生通过问题的探究与思考能够发现两个变量并理解其变化过程，在合作交流中加深理解两个量之间一一对应的变化关系，从而理解函数的概念。并且，这三个探究活动中蕴含了函数模型的三种表达形式：列表法、解析法、图形法，为学习函数的性质设问奠定基础。

（四）归纳小结，讲授新知

在问题导向型课堂中，在层层递进的问题情境理解了函数概念后，还需及时小结与反思。因此，经过三组探究活动得出函数的概念后，笔者设置了温故知新的环节，将函数的概念代入活动探究中的变化过程，让学生结合实例加深理解变量之间的函数关系。例如探究活动一中，变量身高h随着学号x的变化而变化，当学号x取值确定时，身高h也唯一确定，所以身高h是关于学号x的函数，学号x是自变量。

学生通过函数模型的应用过程，再一次理解函数是表示变化关系的模型，感受到数学与生活的紧密关联，提高学生数学建模的应用能力，并通过搭小鱼的模型应用为一元一次函数的学习奠定基础。

三、问题导向教学法与数学建模结合的研究方向

（一）跨学科融合教学

由于学生的知识认知发展水平不同，各学科的学习水平也存在差异，因此我们融合学科知识，建立学科间的知识联系，培养学生的兴起。例如，在学习数学函数模型的时候会有一个在弹簧挂钩下挂重物是弹簧伸长的活动，这是初中物理八年级下学期学习的弹力的内容。学生在学习函数模型的时候，才刚刚接触到物理这一门学科，学生对物理这门学科充满着热情，因此我们数学老师可以请物理老师带学生做一次实验，激发学生学习数学的兴趣，加深学生的记忆，增强学生对一次函数的理解。

（二）信息技术教学的巧用

在信息技术的推动下，网络上出现了越来越多的教学视频，教师们也感受到了信息技术的简便性。微课教学的出现，丰富了教师线上教学的新模式。教師可以在新课前夕在家长群众发布自制的微课，通过微课中设置的导向性问题，引导学生预习新课，让学生有时间可以提前查阅相关资料，培养学生学习的主动性，提高课堂的学习效率。课后教师可以根据课堂教学的重点，设置基础练习与变式训练，培养学生的数学问题意识，让学生数学情境中抽象出数学问题的能力得到大幅度提升，培养学生知识迁移的能力，渗透数学的转化思想。

结束语

问题导向教学法是初中课堂教学的方法，教师要合理设置导向性问题，要注意学生个体之间的差异，注重多层次问题教学活动的开展，设置基础作业与提高任务，培养学生的学习习惯与学习能力。并且，教师要设置适当的反馈机制，多与学生沟通交流，及时调整教学方式与教学内容，培养学生学习的主动性，提高学生的数学建模素养与创新能力。

参考文献：

[1]林小波.应用意识：数学建模的指向——对初中数学教学中数学建模的思考[J].数学教学通讯，2021（32）：58-59.

[2]许艳. 问题导向教学方法在初中数学教学中的实践探究[C]//2020年中小学素质教育创新研究大会论文集.[出版者不详]，2020：266.DOI：10.26914/c.cnkihy.2020.018762.

[3]韩占萍.建模思想在初中数学教学中的应用[J].青海教育，2021（Z2）：73.75.

[4]简相国.初中数学问题导向型微课的设计与开发[J].新课程研究，2021（23）：45-46.