展示基本图形魅力 提升学生数学素养

沈伟明

【摘要】相似三角形是初中几何中重要知识点，相似三角形基本图形的掌握是此知识点的基本要素，以基本图形为研究对象，并将其作为提升学生数学素养的载体，符合学生的认知特点，能收到良好的效果。

【关键词】 基本图形;数学素养;三角形教学

《数学课程标准》在“图形与几何”方面的学习要求是让学生能从较复杂的图形中分解出基本图形，并能分析其中的基本元素及其关系。“图形与几何”的教学从某种意义上讲就是使学生认识基本图形的性质，引导学生运用基本图形的方法去分析问题和解决问题，提升学生的数学素养。因此平面基本图形的认识、储备、运用在相似三角形的教学中显得十分重要。

一、初中学生认知特点

认知心理学认为：人的思维不仅要借助概念，也要借助表象来进行。表象就是人们头脑中出现的事物的形象。初中学生以形象思维为主，形象思维的对象就是表象。如果在学习过程中，让学生重点加工基本图形，那么这些基本图形就可以在学生的大脑中形成比较清晰的表象，从而为解决更复杂的图形打好坚实的基础。面向初中学生，以基本图形为研究对象，并将其作为提升学生数学素养的载体，符合初中学生认知特点。

二、基本图形与基本图形分析法

在几何内容中，图形是重要的表达形式。基本图形一般是指在教材中描述图形定义、公理、定理的图形，如平行线、直角三角形、平行四边形、正方形等。另一类是指一些具有代表性的例题或习题中常见的图形，将同种类型的问题进行合理归纳、梳理，进而形成的一个个基本的图形。利用基本图形分析问题，是几何学习的有效途径。熟悉基本图形的特征、特性，可在描图、画图的过程中培养学生的直观想象素养，在分析问题的过程中培养学生的数学抽象素养，在解决问题的过程中培养学生的逻辑推理素养。相似三角形中出现了大量的基本图形：平行线型、相交线型、母子型、一线三等角型等，通过对这些基本图形为主线开展例题教学和问题解决，能有效提高学生用数学的眼光提出问题、探索问题、解决问题的能力。

三、基本图形模型

相似三角形是苏科版《义务教育教科书数学》九年级下册第六章《图形的相似》的内容，常见的基本图形主要包括以下几种类型：

（一）平行线型

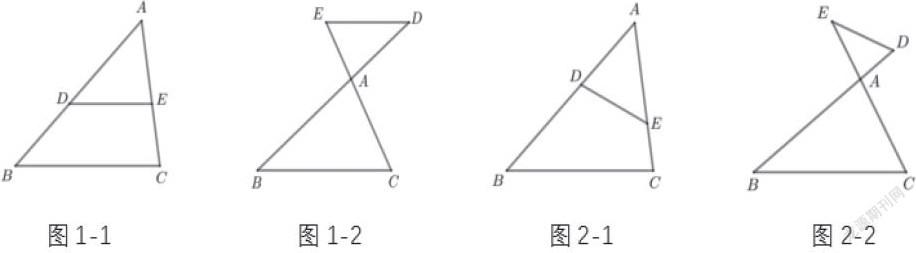
如图1-1、1-2，若DE∥BC，则∆ABC～∆ADE，这种基本图形很像英文字母A、X，因此我们称它们为“A型图” “X型图”。特点：两个相似三角形有两边在同一直线上，第三边相互平行。

（二）相交线型

如图2-1、2-2，若∠AED=∠B，则∆ABC～∆AED，这种基本图形我们称它们为“斜A型图” “斜X型图”。特点：两个相似三角形有两边在同一直线上，有一个公共角或对顶角。

（三）一线三等角型

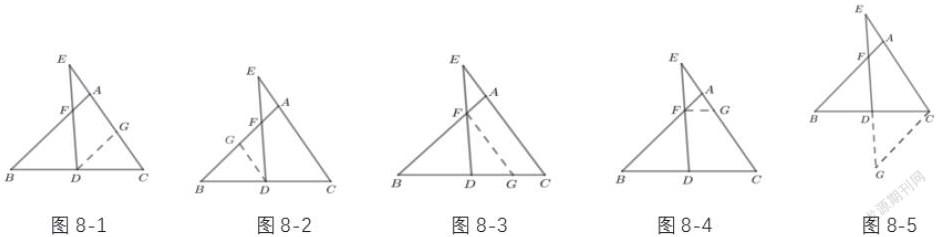
如图3-1，若∠CAD=∠DBE=∠CDE，则∆CAD～∆DBE，这是常见的相似模型，我们称之为“一线三角型”，指的是三个等角在同一条直线上构成的相似模型。这个角可以锐角，也可是直角或钝角，两个相似的三角形可在同侧也可以异侧，如图3-2、3-3、3-4、3-5、3-6。

（四）母子型

将图2-1中DE向下平移到点E与点C重合，如图4-1，则∆ABC～∆ACD，这种相似基本图形称之为“母子型”。特别地，如图4-2令∠ACB=90°，CD是斜边AB上的高时，则∆ABC～∆ACD～∆CBD。“母子型”相似模型也称之为共边共角型，其最为显著的特征为：图形中含有一个公共角和一条公共边，大小三角形错叠相依。

四、运用基本图形解题

（一）直接利用问题中基本图形解题

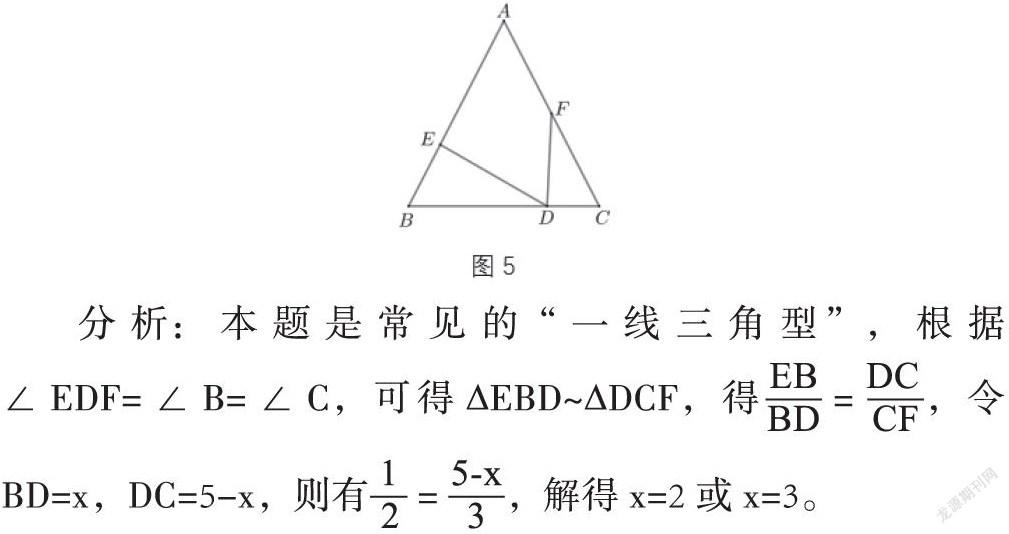
这类题型简明，条件不多，教师只需引导学生找出问题图形中的基本图形，再根据相似三角形性质解题即可。如图5，∆ABC中，AB=AC=6，BC=5，D是BC边上点，以点D为顶点，作∠EDF=∠B，射线DE、DF分别交AB、AC于点E、F，当BE=2，点F为AC中点时，求BD的长。

分析：本题是常见的“一线三角型”，根据∠EDF=∠B=∠C，可得∆EBD～∆DCF，得=，令BD=x，DC=5-x，则有=，解得x=2或x=3。

（二）分離基本图形解题

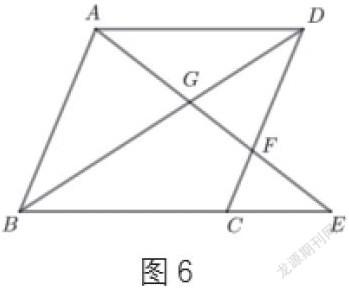
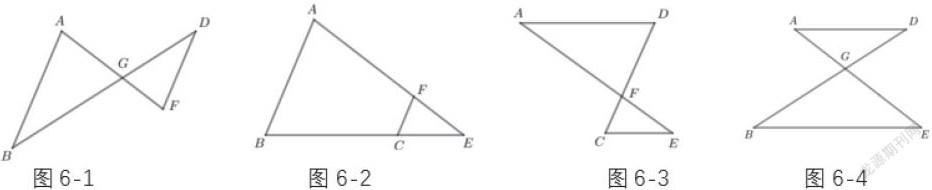
任何一个复杂的几何图形都是由若干个基本图形组合而成的，面对复杂图形要引导学生观察、想象、比较、分析问题图形，精准恰当地从问题图形中分离出基本图形并厘清图形关系，再利用基本图形性质，问题就能迎刃而解。如图6，平行四边ABCD中，点E是BC延长线上一点，AE交BD于点G，交CD于点F，则图中共有多少对相似三角形？

分析 根据AB∥CD，可分离出图6-1和图6-2，得∆ABG～∆FDG，∆ABE～∆FCE，根据AD∥BC，可分离出图6-3和图6-4，得∆ADF～∆ECF，∆ADG∆EBG，根据相似传递性得∆ADF～∆EBA，∆ABD～∆CBD，共六对。

（三）添加辅助线构成基本图形解题

这类题型具有一定的隐蔽性，教学过程中要引导学生认真阅读分析题目信息和图形特点，尝试先找到基本图形的一部分，通过学生的联想、几何直观，再添加辅助线把图形补全，构成完整的基本图形。如图7，∆ABC中，D是BC边中点，E是CA延长线上的点，ED交AB于点F，EF：FD=2：3，求AF：FB的值。

分析：联想已学相似三角形基本图形，通过合作交流，学生们分别找出了几种不同的解法。法一：过点D作DG∥AB交CE于点G，则有∆EFA～∆EDG，∆CDG～∆CBA。法二：过点D作DG∥AC交AB于点G，则有∆EFA～∆DFG，∆BDG～∆BCA。法三：过F点作FG∥EC交BC于点G，则有∆BFG～∆BAC，∆DFG～∆DEC。法四：过点F作FG∥BC交CE于点G，则有∆EFG～∆EDC，∆AFG～∆ABC。法五：过点C作CG∥AB交ED延长线于点G，则有∆EFA～∆EGC，∆CDG～∆BDF。

五、反思感悟

（一）熟悉基本图形，发展学生空间观念

《数学课程标准》要求通过图形的运动，观察、想象、分析图形和思考问题，提高学生研究图形性质的兴趣，发展学生的空间观念。运用基本图形教学时，教师遵循学生认知规律，分别从“直接应用基本图形”“从复杂图形中分离出基本图形”“构造基本图形”三个层次，培养和发展学生的空间观念，达到发展学生思维、促进学生技能提高的目的。

（二）掌握基本图形，建立学生几何直观

《数学课程标准》指出“几何直观是指利用图形描述和分析问题，借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用”。它表明，在整個数学教学中都应该重视几何直观，培养几何直观能力应该贯穿义务教育数学课程的始终。在教学中要有意识地强化对基本图形的运用，不断地运用这些基本图形去发现、描述问题，理解、记忆结果，借助对基本图形的分析与学习，学会用图形思考、想象问题是研究数学，也是学习数学的基本能力。这种几何直观能力能使我们更好地感知数学、领悟数学。

（三）运用基本图形 形成学生模型思想

模型思想是数学课程标准提出的核心理念之一，数学教育家罗增儒教授提倡在学习数学的过程中，要善于对新问题展开联想，辨别它是否属于某个已经掌握的类型，如果不直接属于，那么能否进行一些变化，使之属于某个类型。数学模型的形式是多样的，有方程、不等式、函数等代数模型，也有几何中融合着特殊位置关系和特殊数量关系的基本图形，还有统计与概率中数据模型和概率模型。在相似三角形教学中将常见几何图形抽象为为平行线型，相交线弄，一线三角形等最具代表性的基本图形，形成数学模型，使之成为学生解决几何问题的重要工具， 在图形与几何的教学中，将模型思想渗透到教学之中，发展了学生的创新意识有应用意识，提升了学生分析问题和解决问题的能力。

结语

教师要多引导学生积累常见的基本图形知识以及构建基本图形的方法，注重对基本图形的分析和挖掘，提高学生发现问题、分析问题和解决问题的能力，促进学生数学核心素养的提升。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准.北京：北京师范大学出版社，2011.

[2]彭靖东.解析基本图形 树立模型意识.中学数学研究，2020.

[3]张宣.以基本图形学习为主线的单元教学设计.上海中学数学，2020（6）.

[4]邓紫琳.感悟基本图形，提升初中学生数学解题能力.数学教学通讯，2020.