高中数学函数教学中化归思想的运用

高春明

【摘要】将化归思想融入到数学函数的教学中，就是将复杂、深奥、晦涩知识点转化容易让学生理解的形式，展现给学生，是高中输血函数教学最常使用的教学手段之一.笔者结合多年的数学教学经验，就如何将化归思想融入到高中数学函数教学活动中，提出几点看法和建议，以供参考.

【关键词】高中数学;函数教学;化归思想

函数是高中数学体系的重要组成部分，函数的学习质量，直接影响着高中生的高考成绩.随着新课改的不断深入，当下的高中数学教师必须要不断的转变个人的教学理念，革新教学方式，将高中生放在课堂的首要位置，采用更加灵活的教学手段，带领高中生更加高效的开展数学函数学习，高中数学教师，也应合理运用划归思想，实现函数问题的去繁存简，有效锻炼学生的思维逻辑，提升其对函数基础知识的掌握程度，让其数学成绩更上一层楼.

1 借助划归思想，明确重难点知识

函数的内容抽象且复杂，需要高中生具备良好的逻辑能力和思维能力，才能够面对各种各样的函数难题.数形结合能够通过函数图形，将函数的性质、定义等更直观、全面的向学生展示，加快其对于函数的掌握速度，提高其学习效率[1].

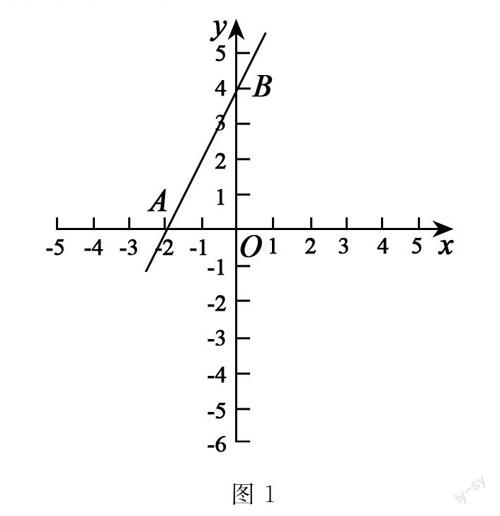
例如 筆者在向学生解析 “已知直线的函数为y=2x+4，求出该函数的斜率（即：k值），并判断该函数所经过的象限有哪些？”时，笔者先带领学生对题目的已知条件进行了分析，并将该函数转换为2x-y+4=0，并根据公式k=-A/B，则求出k=2.随后，引导学生建立直角坐标系，求出该一次函数直线与X轴和Y轴的交叉点，即：设函数与X轴的交点坐标为A（x，o），函数与Y轴的交点的坐标为B（0，y），便得出A点的坐标为（-2.0），B点的坐标为（0，4）.最后将这两点坐标在直角坐标系上描出，连接A点与B点划出一条直线，即为y=2x+4的函数图像，如图一所示.最后根据图像即可判断出该函数过一二三象限.巧妙利用化归思想，可更为直观的向学生们展示知识的重难点，帮助学生快速掌握关键信息，提升课堂教学效率.

2 借助化归思想，将陌生的问题熟悉化

函数的题目多种多样，但是其考点大致相同.也就是说，同一个函数知识点，会以不同的题目类型进行展示，但陌生的题型，会让学生感觉恐慌，甚至不知所措，这就需要学生在熟练掌握函数知识的同时还需要具有逻辑思维能力.因此，采用化归思想，将陌生的问题熟悉化，可以帮助学生快速分析题目的已知条件和题目所涵盖的考点，进而加快其解题速率[2].

例如 笔者在讲解对数函数时，先带领学生将陌生的对数函数转变为指数函数，并在指数函数性质的基础上，分析对数函数的性质，并对比二者性质，找出两种函数的相同点和不同点.最后，笔者带领学生绘制对数函数图像，再根据图像内容分析对数函数的性质，加深学生的理解.对数函数的图像如图二所示.化归思想的妙用，在一定程度上，能够提升学生对数学知识的理解，帮助学生掌握良好的解题方式，转换思路，从熟悉的角度解决陌生问题，提升解题效率.

注：红色线为f（x）=log2x，蓝色线为f（x）=log12x

3 借助化归思想，将复杂的问题简单化

化归思想能够将复杂的问题变得简单化.问题的难度得到降低，那么学生的解题效率自然就可以得到提升.所以，在实际教学的过程之中，高中数学教师必须要学会带领学生合理的使用化归思想，有效转化已经存在的问题.用理智的思维去看待问题，分析问题，选择合适的方式去解决问题.在日常教学时，数学教师可以在课堂之中多增加一些划归思想的数学题目，让学生得到锻炼，从而提升解题技能.

例如 笔者在带领学生解答“已知抛物线y=x2+4ax-4a+3，y=x2+2ax-2a至少有一条与x轴相交，求实数a的取值范围”时，先设方程x2+4ax-4a+3=0有两个不相等的实数解△1=16a2-4（-4a+3）>0 ，得到a<-32或a>12;其次，设方程x2+2ax-2a=0有实数解△2=4a2+8a>0，得到

a>0或a<-2，最终求得a的取值范围为（-∞，-32）∪（0，+∞）.如若不使用划归思想，直接开始解题，就需要对题目进行分类讨论，导致解题过程较为繁琐，容易出错，加大了解题难度.其次，题目的难度越高，学生的解题兴趣就越低.但是如果选择用化归思想去解决问题，将改题目看做：“两条抛物线和x轴都不相交”，就可以降低解题难度，提升学生的解题速度.因此，在解题的过程之中，教师可以带领学生换个角度思考问题，将问题简单化，减少失误率，进而提高其数学成绩.

4 借助化归思想，实现动静转化

动静转化，是化归思想中的常用思想.在教学的过程之中，数学教师可以让学生归纳函数数据，建立数学模型.在动静转化的过程之中，发现对应关系.借助划归思想，帮助学生掌握数学变量和因素之间的关系，从而在最短的时间内，找到问题解决办法.

例如 笔者在分析：“函数f（x）=x2+ax+3.（1）当x∈R时，f（x）≥a恒成立，求a的取值范围;（2）当x∈[-2，2]时，f（x）≥a恒成立，求a的取值范围.”题目时，因为有“至少有一个零点”这一条件，增加了解题的难度，因此不得不对改题目进行分类讨论，对解题难度有一定程度的增加.但这道题目也可以运用化归思想来解决，即：从方程的角度入手，把函数的零点个数的问题，转化成函数图像交点问题.将函数转变成方程，再将方程转化为函数，这样就可以快速的该题目.具体解题方法如下：（1）因为x∈R，f（x）≥a恒成立，所以x2+ax+3-a≥0恒成立，则Δ=a2-4（3-a）≤0，得-6≤a≤2.所以当x∈R时，f（x）≥a恒成立，则a的取值范围为[-6，2].（2）f（x）=

x+a22+3-a24.讨论对称轴与[-2，2]的位置关系，得到a的取值满足下列条件：

-a2≤-2，f（-2）≥a或-2<-a2<2，3-a24≥a或-a2≥2，f（2）≥a，即a≥4，7-2a≥a或-4

解得-7≤a≤2.所以当x∈[-2，2]时，f（x）≥a恒成立，则a的取值范围为[-7，2].由此可见，利用化归思维解题，既可以开拓解题思路，有效提升学生的解题速率，又能够提升学生的创新能力，培养其的数学思维，为其走向成功之路打下夯实的基础.

5 结语

对于高中函数教学而言，化归思想的应用是必不可少的.但是在使用的过程之中，高中数学教师必须要明确化归思想和实际教学的区别，减少学生对化归思想的盲目依赖，帮助学生培养良好的解题思路，带领学生构建完善的学习框架，提升学生们的学习能力，提升学生学习数学的积极性.最后，作为一名高中数学教师，要时刻保持进步的心态，不断学习先进的教学经验，创新教学方法，灵活开展教学活动，方能提升教学效率，促进学生全面发展.

参考文献：

[1]石磊.化归思想在高中数学函数学习中的运用探讨[J].中外交流，2019，26（14）：191.

[2]肖燕.论化归思想在高中数学函数学习中的运用[J].赤子，2018，（7）：247.