“分享一创生” 式下自信课堂研究一以成都市武侯区2021年八下零诊第2 0题为例

万人杰 袁苓岚

【摘 要】 新课改与“双减”背景政策下，对学生的综合素养和教师的课堂教学提出了更高的要求，全面发展并高效开拓学生思维能力是关键，其中一题多解能快速培养学生深度思考的能力，并通过多种方法择优使用提升学生批判意识，达到“分享一创生”教学模式的本质目标，

【关键词】 分享创生;一题多解;自信课堂

在“双减”背景下，为了保证学生的学习质量，除了对老师的素质要求更高以外，对学生的数学核心素养也提出了更高标准.在培养学生善以数学的角度和思维方式去看待客观世界，并进行理性地分析、严密地求证，富有逻辑性的推理和清晰准确表达的过程中，理性和逻辑始终贯穿其中，几何题目是数学核心素养的综合体现，灵活多变又妙趣横生，新颖的背景和丰富的内容使得几何综合题目成为了数学核心素养考查的重中之重.几何题目的一题多解更能激发学生的数学学习兴趣、开发学生的思维、灵活迁移已学知识解决问题、熟练识别基本图形和应用性质，并且促进学生学以致用的创新能力，“分享一创生”教学模式下的自信课堂旨在培养学生深度思考的能力和批判意识，建立逻辑和理性的思维模式，下面以成都市武侯区2021年八下零诊第20题为例，谈一谈基于“分享一创生”教学模式下的自信课堂研究和思考.

1 试题呈现

已知点E是正方形ABCD的边CD上的动点，连接AE，过点A作AFIAE，交CB的延长线于点F.

（1）如图1，求证：FB=ED;

（2）点G为正方形ABCD的对角线BD上一点，连接AG，GC，GF，且GC=GF.

①如图2，求∠GFA的度数;

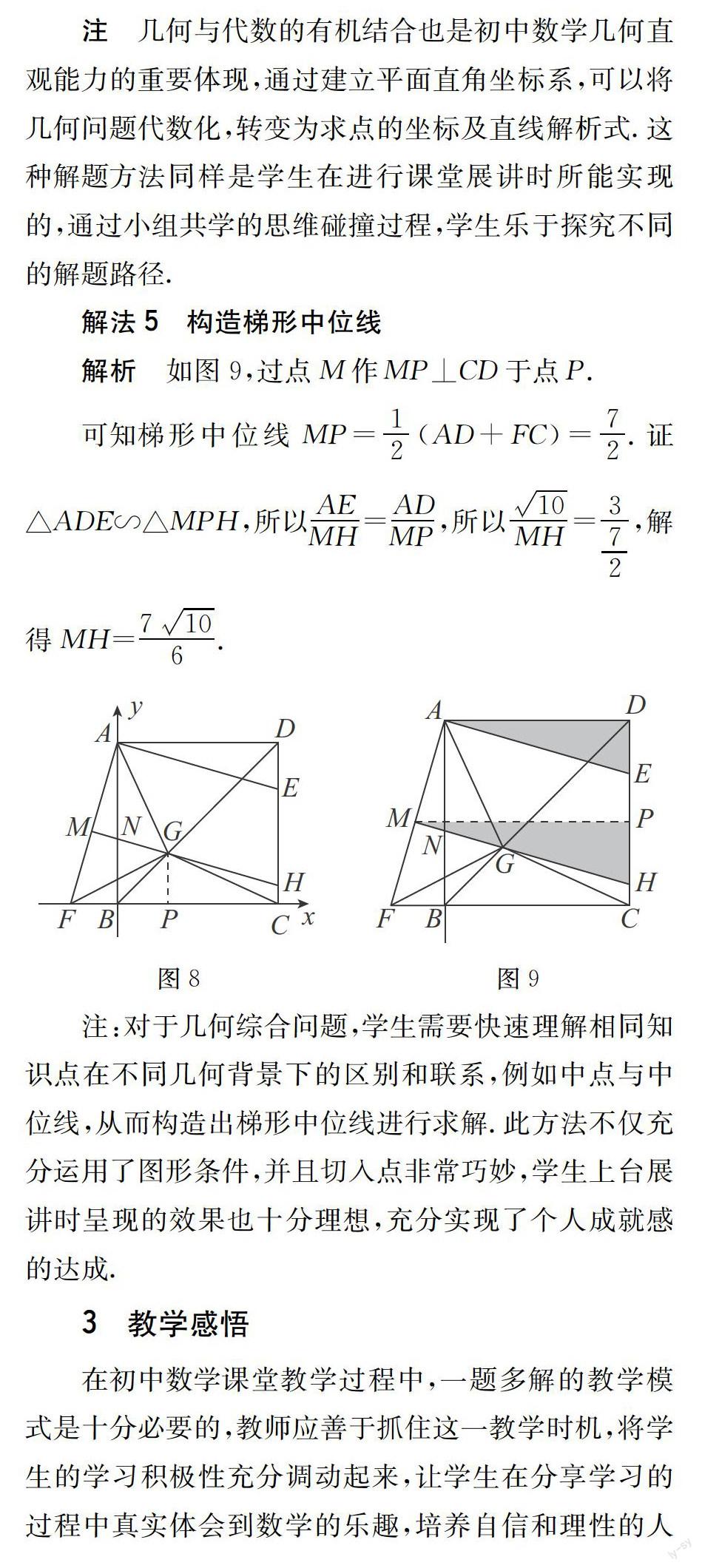
②如图3，过点G作MH∥AE，分别交AF，AB，DC于点M，N，H.若AB=3，BF=1，求MH的长.

2 解法探究

本题出自2021年成都武侯区期末零诊卷第20题，作为一道四边形综合题，考查了正方形的性质，全等三角形的判定和性质，等腰直角三角形的判定和性质，勾股定理等几何知识.对于第（2）②小问，学生需要由等腰三角形的三线合一性质得出MH是AF的垂直平分线，从而利用勾股定理列出方程进行求解.在实际检测中，学生高度紧张的心理状态导致难以从复杂的几何图形中剖析出相关条件与结论，找寻不到解题突破口，做出错误的辅助线.

注 对于相似知识的运用，并不属于八下零诊考查范围，在相同的题目背景下，对不同几何特征的把握和处理就会选择不一样的解法，正是在问题解决的过程中，学生的分析能力、知识迁移能力以及创造性思维得到培养，同时也满足了不同层次学生的学习需求，“分享一创生”教学模式下的初中数学自信课堂的核心得以体现.

注 在初中数学学科的六大核心素养中，几何直观能力占据着重要地位，它需要同学们对基本图形、相应的几何性质、常见的辅助线构造方法掌握熟练，在遇到具体问题时能够将复杂的几何图形拆分成几个基本图形，从而化繁为简，将题目条件不断转化为所求结论.

注 几何与代数的有机结合也是初中数学几何直观能力的重要体现，通过建立平面直角坐标系，可以将几何问题代数化，转变为求点的坐标及直线解析式.这种解题方法同样是学生在进行课堂展讲时所能实现的，通过小组共学的思维碰撞过程，学生乐于探究不同的解题路径.

注：对于几何综合问题，学生需要快速理解相同知识点在不同几何背景下的区别和联系，例如中点与中位线，从而构造出梯形中位线进行求解.此方法不仅充分运用了图形条件，并且切人点非常巧妙，学生上台展讲时呈现的效果也十分理想，充分实现了个人成就感的达成.

3 教学感悟

在初中数学课堂教学过程中，一题多解的教学模式是十分必要的，教师应善于抓住这一教学时机，将学生的学习积极性充分调动起来，让学生在分享学习的过程中真实体会到数学的乐趣，培养自信和理性的人格特质.在师生、生生之间的交流和思维碰撞中，“分享一创生教学模式所提倡的学生和教师身份灵活转换，讓原有的老师的“教和学生被动的“学”，老师作为教育者，学生作为被动的接受者这样传统不对等的关系变得更加平等.教师学生、学生教师的角色转换让学生的学习由积极主动内化到输出.

整个学习过程中不只有听，更有思考时思维火花的碰撞，选择时方法优劣的判断，讲解时择优讲解的抉择，以及学习过程中个人成就感的达成，久而久之，学生的学习主动性将会不断提升，课堂教学氛围更加融洽，班级内的小老师也会愈发涌现出来.一旦学生愿意真正投入学习，成绩提升就是自然而然的结果，而学生不仅学会了知识，掌握了技能，更重要的是让自己学会学习，成为一名“眼里有光，脸上有笑，心中有人”的自信少年，基于“分享一创生”教学模式下的自信课堂得以实现，

当然，如果只是偶尔对个别题目进行一题多解的处理并不能达到理想的效果，要真正实现“‘分享一创生，教学的初中数学自信课堂”的价值和目标，还需要借助分享学习型课堂所倡导的小组共学，师生互助等生讲生学学习模式作为落脚点，同时也需要对一题多解的模式进行更加深入和持续的研究.

【2019年四川省普教科研资助金重点课题“‘分享一创生教学的理论与实践”研究成果，】

参考文献：

[1]张玉华，牟天伟，潘超.深度学习视域下初中数学分享学习型课堂研究[J].重庆第二师范学院学报，2021（ 34）.

[2]杨德军.试析在初中数学一题多解中如何培养学生的数学思维[J].考试周刊，2019（A3）.

[3]中华人民共和国教育部.全日制义务教育数学课程标准（201 1年版）[M].北京：北京师范大学出版社，201 1.