分类例析“嵌套函数”的零点问题

李发明

(山东省泰安第一中学，271000)

在复合函数中,我们把一个函数自身对自身复合所得到的函数叫做嵌套函数,也叫迭代函数.其中函数的零点问题是命题的热点,求解时通常先“换元解套”,将复合函数拆解为两个相对简单的函数,借助函数的图象、性质求解.本文通过实例谈谈嵌套函数常见的三类零点问题的求解策略,以期对广大备考学子有所帮助.

一、求嵌套函数的零点个数

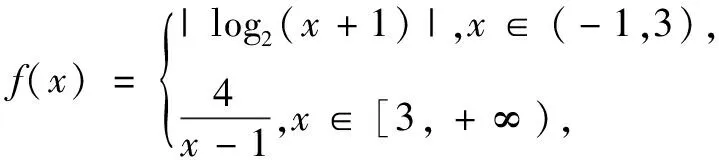
当t=1时，由图1易知方程f(x)=1有3个不等实根；当t=5时，由图1易知方程f(x)=5有1个实根.

综上，g(x)有4个零点.

评注例1中f(x)为分段函数,若直接写出g(x)的表达式考虑问题非常繁琐.本解法用换元法将g(x)分拆为g(t)=f(t)-1和t=f(x)两个相对简单的函数,借助f(x)的图象大大简化了运算步骤.由此可见“换元解套”是解决嵌套函数的利器.

二、求分段函数中参数的取值范围

解当a<0时，f(x)的图象如图2(a),f[f(x)]=0不可能有8个不等实根.

当a=0时，f(x)的图象如图2(b),f[f(x)]=0也不可能有8个不等实根.

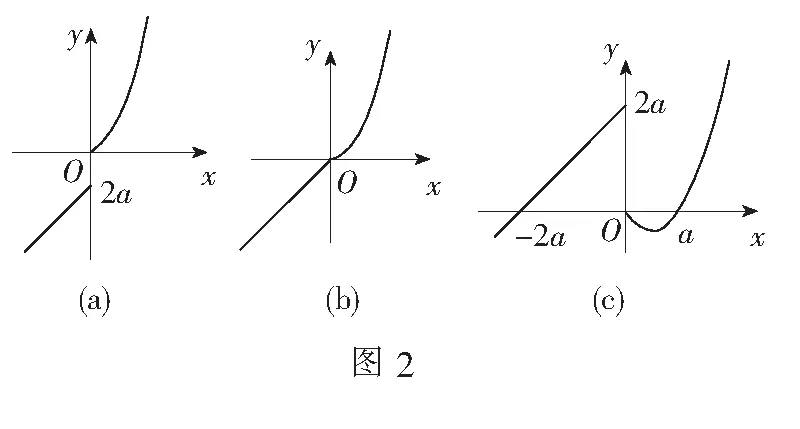
当a>0时,f(x)的图象如图2(c).令t=f(x),由f(t)=0,观察图象易知t=-2a或0或a.

若t=0时,易知方程f(x)=0有3个不等实根.

当t=a时,即观察易知f(x)的图象与y=a交于两个不同的交点,即方程f(x)=a有2个不等实根.

综上，a>8.

评注本题f(x)表达式中含有参数,图象有3种情况.求解时需对参数a分类讨论,找到符合题意的参数取值范围.

三、求嵌套函数(或方程)中参数的取值范围

解令t=f(x),则g(x)=0变为关于t的一元二次方程t2-4t+m+1=0,它至多有t1,t2两不等实根.

因为g(x)=0有8个不等实根,而由图3知f(x)=t的实数根个数可能为0,1,2,3,4,故只存在一种情况,即f(x)=t1和f(x)=t2均有4个交点符合题目要求.于是原问题等价于一元二次方程t2-4t+m+1=0在(0，3]上有两个不等实根.

令h(t)=t2-4t+m+1,则

解得2≤m<3.

解令t=f(x),则由图4可知当a≥-1时，方程f(t)=a有2个不等实根t1,t2,且t1<-1,t2≥-1.由于f(x)=t1有1个实根，f(x)=t2有2个实根，所以a≥-1时符合要求.

当a<-1时，方程f(t)=a有1个实根t0,且tt0<-1，此时方程f(x)=t0只有1个实根，不符合要求.

综上，a≥-1.

(A)函数f(x)的零点个数为2

(C)函数f(x)无最值

(D)函数f(x)在(0,+∞)上单调递增

解由图5易知,选项A对,选项C对,选项D错.

综上,选ABC.

例6如图6，已知f(x)是定义域为R的偶函数,且当x≥0时，

若关于x的方程[f(x)]2+af(x)+b=0有且仅有6个不同的实数根,则实数a的取值范围是______.

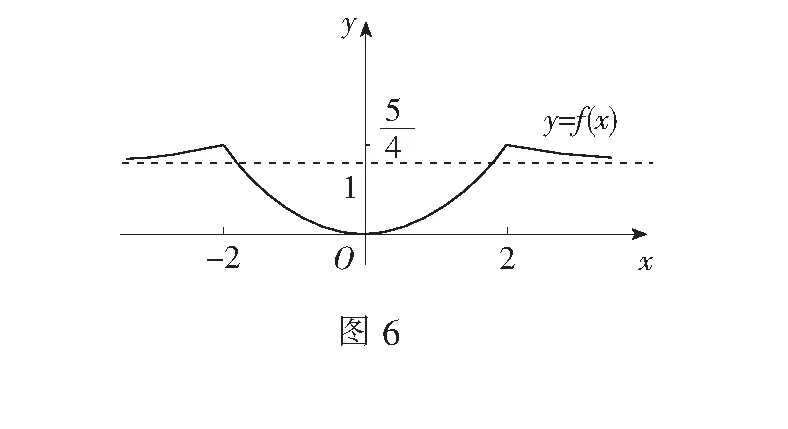
解令t=f(x),则题设方程为t2+at+b=0,这是关于t的一元二次方程,至多有两个不等实根t1,t2.因为原方程有6个不等实根,所以存在两种情况符合题意:

(A)f(m)≤0

(B)f(m)可能大于0

(C)m∈(-∞,-1]

(D)m∈(-∞,-1]∪(0,e2]

解不等式f(m)≤0，如图7，由f(x)的图象知m≤-1或0

综上，选AC.

通过以上例题的求解,我们可以体会到“换元解套”在嵌套函数问题中的必要作用,最终回归到基本初等函数才是我们解决函数题的归宿.