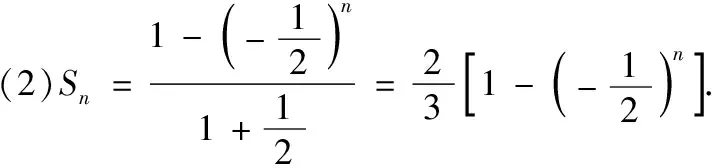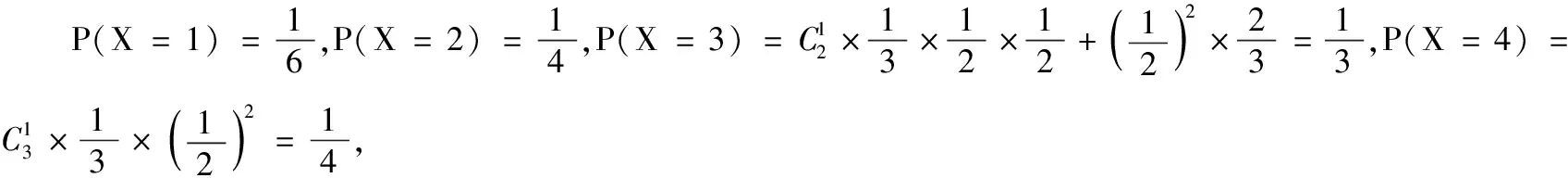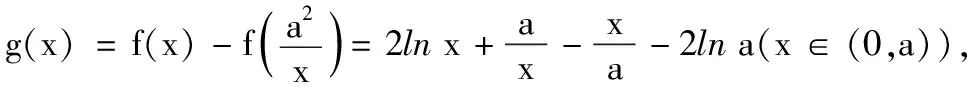高三数学综合测试

一、单项选择题(本大题共8小题，每小题5分，计40分)

1. 设集合A={-1,0,1},B={x|lg(x+2)>0},则A∩B=( )

(A){-1,0,1} (B){0,1}

(C){1} (D)(-1,+∞)

2.已知复数z与(z+2)2+8i都是纯虚数,则z=( )

(A)2 (B)-2 (C)2i (D)-2i

3.已知甲、乙、丙三人均去某健身场所锻炼,其中甲每隔1天去一次,乙每隔2天去一次,丙每隔3天去一次.若2月14日三人都去锻炼,则下一次三人都去锻炼的日期是( )

(A)2月25日 (B)2月26日

(C)2月27日 (D)2月28日

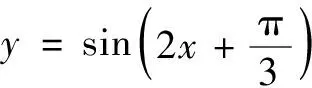
(A)-sin 4x(B)sinx

5.某学校每天安排四项课后服务供学生自愿选择参加.学校规定:(1)每位学生每天最多选择1项;(2)每位学生每项一周最多选择1次.学校提供的安排表如下:

时间周一周二周三周四周五课后服务音乐、阅读、体育、编程口语、阅读、编程、美术手工、阅读、科技、体育口语、阅读、体育、编程音乐、口语、美术、科技

若某学生在一周内共选择了阅读、体育、编程3项,则不同的选择方案共有( )

(A)6种 (B)7种

(C)12种 (D)14种

(A)-10 (B)5 (C)35 (D)50

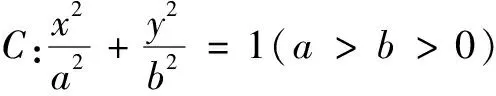
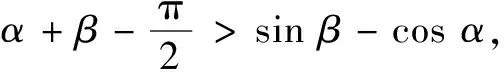
(A)sinα>sinβ(B)cosα>cosβ

(C)cosα>sinβ(D)sinα>cosβ

二、多项选择题(本题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)

9.下列函数中最小值为6的是( )

(C)y=3x+32-x

10.已知直线l与平面α相交于点P,则( )

(A)α内不存在直线与l平行

(B)α内有无数条直线与l垂直

(C)α内所有直线与l是异面直线

(D)至少存在一个过l且与α垂直的平面

PiP1P2P3P4P5P6P7P8xi15.115.215.315.415.515.415.413.4yi15.114.214.314.414.515.414.415.4zi2012131516141218

(C)P1是孤立点 (D)P2不是孤立点

12.定义:在区间I上,若函数y=f(x)是减函数,且y=xf(x)是增函数,则称y=f(x)在区间I上是“弱减函数”.根据定义可得( )

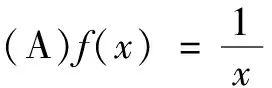
三、填空题(本题共4小题,每小题5分,计20分)

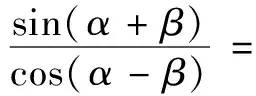
15.写出一个同时具有下列性质① ② ③ 的三次函数f(x)=______.

①f(x)为奇函数;②f(x)存在3个不同的零点;③f(x)在(1,+∞)上是增函数.

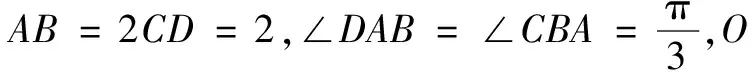
四、解答题(本题共6小题,计70分.解答应写出文字说明、证明过程或演算步骤)

18.(本小题满分12分)设Sn是等比数列{an}的前n项和,a1=1,且S1,S3,S2成等差数列.

(1)求{an}的通项公式;

(2)求使Sn≤3an成立的n的最大值.

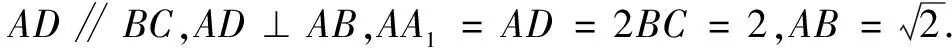
(1)求证:BD⊥C1F;

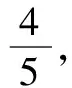
(1)求C的方程;

(2)过点(3,0)的直线l交C于P,Q两点,过点P作直线x=1的垂线,垂足为A.证明:直线AQ过定点.

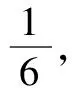
(1)求恰好在第二次射击后击落飞机的概率;

(2)求击落飞机的命中次数X的分布列和数学期望.

(1)讨论f(x)的单调性;

(2)若f(x1)=f(x2)=2(x1≠x2),证明:a2

参考答案

一、单项选择题

1.B;2.C;3.B;4.B;5.D;

6.A;7.A;8.D.

二、多项选择题

9.BC;10.ABD;11.ABD;12.BCD.

三、填空题

四、解答题

17.若选①.由余弦定理,得

c2=a2+b2-2abcosC

=9,

所以c=3.

若选②,由余弦定理,得

所以c=3(舍),c=5.

又b>a>c,故∆ABC为锐角三角形.

19.(1)在直四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,又BD⊂平面ABCD,所以AA1⊥BD.

又因为AA1,AC⊂平面ACC1A1,AA1∩AC=A,所以BD⊥平面ACC1A1.因为C1F⊂平面ACC1A1,所以BD⊥C1F.

当直线l斜率存在时,设其方程为y=k(x-3),点P(x1,y1),Q(x2,y2),则点A(1,y1).

(2)X的可能取值为1,2,3,4.

当a≤0时,f′(x)≥0恒成立,f(x)在(0,+∞)单调增.

当a>0时,f′(x)<0的解集为(0,a),f′(x)>0的解集为(a,+∞).

综上,当a≤0时,所以f(x)的单调增区间为(0,+∞),无减区间;当a>0时,f(x)的单调增区间为(a,+∞),单调减区间为(0,a).

(2)因为f(x1)=f(x2)=2(x1≠x2),所以f(x)min=f(a)=lna+1<2,解得a∈(0,e).