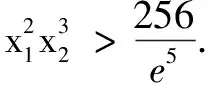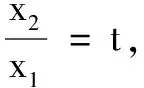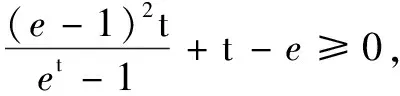增量代换法求解零点不等式问题
王国军 吴瑞环
(河北省石家庄市第二中学,050000)
导数是研究函数性质的核心工具,在研究函数性质的过程中,零点是最为核心和关键的问题.近几年,零点问题是高考和模拟考试的热点问题,一类涉及函数零点的不等式备受命题人青睐,成为理所当然的把关压轴题.学生对于这类问题并不陌生,也知道需要消元转化为一元函数不等式求解.但如何才能将不能显性表示的零点表示出来,成为压倒骆驼的最后一根稻草.本文挑选几例模拟试题,给出增量代换法表示零点的可操作性过程,供大家高三复习备考.
一、增量法解决零点问题的过程
先用一道高考真题,给出增量代换法解决问题的具体过程.
例1(2010天津高考题)设函数f(x)=xe-x,x∈R.若f(x1)=f(x2),且x1≠x2,求证:x1+x2>2.
分析由已知条件得到一个方程,且含有超越结构,此时x1,x2无法具体表示出来;为表示出x1,x2,需要借助x1,x2之间的新的运算关系,构造方程组求解.
解不妨设x1 第一步:引入参数t作为增量. 第二步:用增量表示零点x1,x2. 第三步:将多元不等式转化为关于增量的一元函数不等式. 第四步:证明一元函数不等式,使问题获解. 所以g(t)>2,即x1+x2>2.得证. 1.利用零点之比,引入增量参数 例2已知函数f(x)=lnx-ax+1(a∈R). (1)讨论函数f(x)的单调性; 分析第(1)问需对参数进行简单的分类讨论;第(2)问要能想到对目标不等式取自然对数进行转化,再利用增量代换法处理. 解(1)当a≤0时,易见函数f(x)在(0,+∞)单调增. 例3已知函数f(x)=lnx-ax+2(a∈R)有两个零点x1,x2. (1)求实数的取值范围; 解(1)(0,e).(过程略) 综上,得证. 2.利用零点之差,引入增量参数 例4已知a>0,函数f(x)=xex-ax3+3ax+1. (1)讨论函数f(x)极值点的个数; (2)若函数f(x)有三个极值点x1,x2,x3,且x1 x3+(e2-2e)x2+x1≥e2-e. (2)易知f′(x)=(x+1)[ex-3a(x-1)]. 由(1)可知x1=-1,要证x3+(e2-2e)x2+x1≥e2-e,只需证x3+(e2-2e)x2≥e2-e+1. 令h(t)=(e-1)2t+(et-1)(t-e),其中t>0,则h′(t)=(t-e+1)et+e2-2e,h″(t)=(t-e+2)et.所以当0 因为h′(0)=e2-3e+1>0,h′(1)=0,故h′(e-2)<0,从而存在唯一t0∈(0,e-2),使得h′(t0)=0.所以当0 又h(0=0,h(1)=0,所以当t>0时,h(t)≥0,原不等式成立. 数学题目千变万化,自然解法也会千姿百态,用一种方法包打天下是不切实际的.数学复习目的之一是提高学生的数学综合能力,在教学上需要提升学生分析问题和解决问题的能力,这单靠机械地刷题和题海战术是很难真正实现的.高三复习教师要注重双基本质的挖掘,关注学生思维上的短板,充分暴漏自己解题的思维历程,教给学生如何进行数学的思考和程式化的解题过程.这样的课堂教学才真正有助于学生理解知识本质、掌握基本方法,有利于学生形成有论据、有条理的数学思维习惯,培养学生的逻辑推理素养.


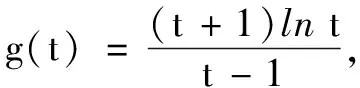



二、增量引入的常见方法