一道“强基”题的柯西不等式解法

史多动

(甘肃省高台县职业中等专业学校，734300)

一、试题呈现

这是2021年1月清华大学中学生标准学术能力诊断性测试(THUSSAT)新高考第15题.本文从柯西不等式及其变式多角度揭示求解这类问题常用的基本思路和方法.

二、解法探析

1.基础知识

二维柯西不等式 设a,b,c,d∈R,则

(a2+b2)(c2+d2)≥(ac+bd)2,

等号当且仅当a∶c=b∶d时成立.

变式设a,b,c,d均为正数,则

等号当且仅当a∶c=b∶d时成立.

2.多视角求解

(1)配凑视角

分析1根据已知式和所求式的结构特征,利用柯西不等式配凑,将已知等式的两边都加上3,使含有a的项的分子出现a+1,然后进行常数代换,利用二维柯西不等式求得最值.

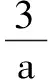
分析2根据已知式和所求式的结构特征利用柯西不等式的变式配凑,将所求式变形、配凑出含有已知式中的项,利用二维柯西不等式变式求解。

(2)消元视角

分析3由条件消去a,得到关于b的式子,再按柯西不等式的形式配凑、求解.

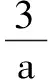
评注(1)亦可消去b转化为a的式子进行求解(此处从略).

(2)消去b得到关于a的式子后，亦可用柯西不等式的变式求解.具体过程如下：

(3)换元视角

分析4根据已知式进行和差换元(均值换元),并代入所求式,得到关于新元的式子,进行“1”的代换,利用柯西不等式求解.

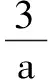
分析5根据已知式结合平方关系进行三角换元,再利用柯西不等式的变式求解.

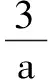
由上可见,对典型试题进行多解探究,既能梳理解决这类问题的一般方法,寻求解答此类问题的通性通法,揭示问题的本质和一般规律,又能拓宽学生的知识面,权衡解法优劣,积累解题经验,提高解题效率.此外还能沟通知识间的联系,厘清知识脉络,构建完整的知识体系,使知识、方法、能力融为一体,学会数学地思考问题,开发智能,优化数学思维品质.