蝴蝶定理的妙用及变式推广

吴宏考

(浙江省宁波市北仑区明港高级中学,315800)

一、理论背景

1.圆中的蝴蝶定理

蝴蝶定理是平面几何中最优美的结论之一,这个定理因图形像一只蝴蝶而得名.该定理的证明有较多方法,这里介绍简便易懂的面积法证明[2].

蝴蝶定理如图1,点M是圆O中弦AB的中点,CD,GH是过点M的两条弦,连结CH,DG分别交AB于点P,Q,则MP=MQ.

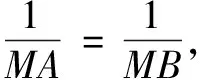
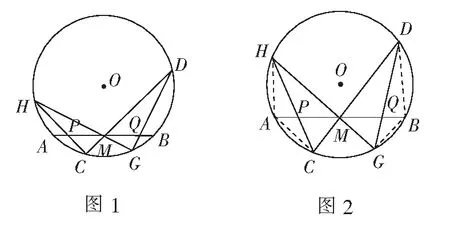
如图2,连结AH,AC,BG,BD,由面积及相似三角形关系,可得

综上,得证.

2.椭圆中的蝴蝶定理

推广1如图3,AB是二次曲线Ω的一条弦,O是AB的中点,过O作Ω的两条弦CD和EF,其中C,E位于AB的同一侧,直线CF和DE分别交AB于点P,Q,则有OP=OQ.

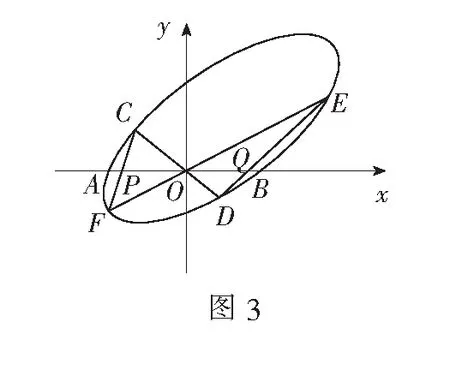
证明建立直角坐标系如图3,不妨设A(-m,0),B(m,0),P(xp,0),Q(xQ,0),由于二次曲线过点A,B则可设二次曲线的方程为

x2+uy2+vxy+wy-m2=0.

另设直线CD,EF的方程分别为y=k1x,y=k2x,则过点C,D,E,F的二次曲线为x2+uy2+vxy+wy-m2+λ(k1x-y)(k2x-y)=0,其中λ为实数.

令y=0,则有xP,xQ是方程(1+λk1k2)x2-m2=0的两个根.由韦达定理,可知xP+xQ=0,故OP=OQ.结论得证.

二、应用举例

笔者在解题中发现,解析几何中有些与比值有关的问题,如果运用“蝴蝶定理”会更加容易解决,不仅使得计算大大简化,而且可以窥视命题的出发点与根源,深化我们对问题本源的理解与把握.

(1)求椭圆C的方程;

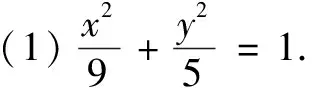
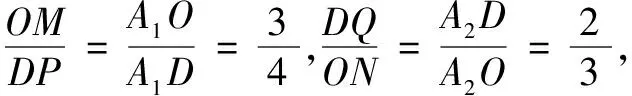
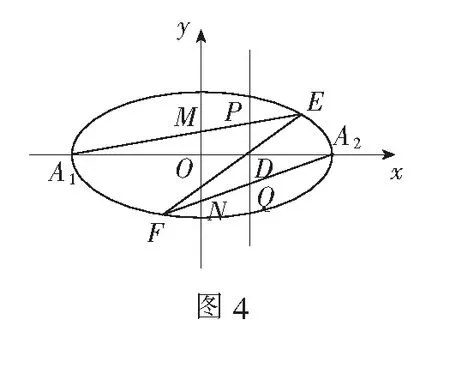
评注此题有较多解法,文[3]提供了3种解法从计算量来说本解法直接由蝴蝶定理来思考,可做到一步到位.

(1)设动点P满足PF2-PB2=4,求点P的轨迹;

(3)设t=9,求证:直线MN必过x轴上的一定点(其坐标与m无关).

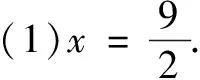
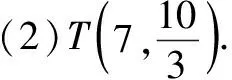
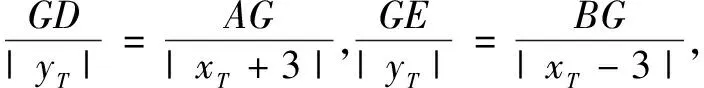
三、蝴蝶定理的变式推广

推广2在椭圆中,过弦AB的端点作曲线的切线相交于点M,过点M作直线l∥AB,CD,EF为过点M的两条弦,直线CE,DF交直线l于点P,Q,则有MP=MQ.

证明如图6,以点M为原点,以直线l为y轴建立平面直角坐标系,设曲线方程为

Ax2+Bxy+Cy2+Dx+Ey+F=0.

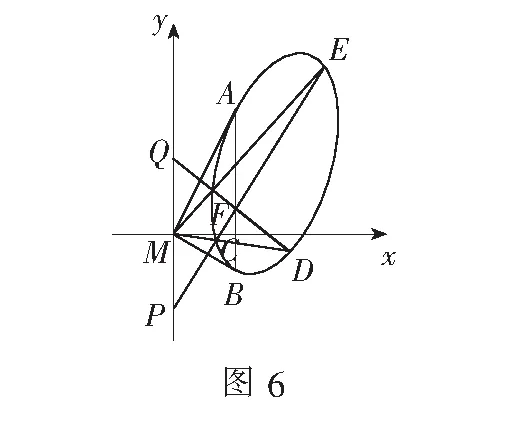
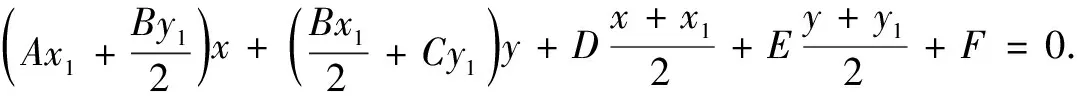
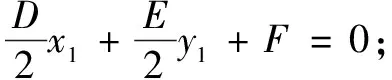
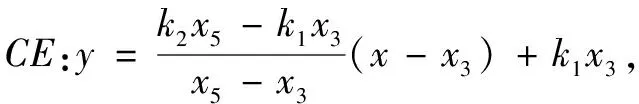
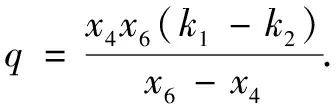
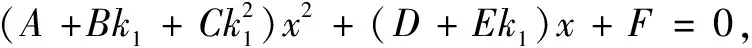
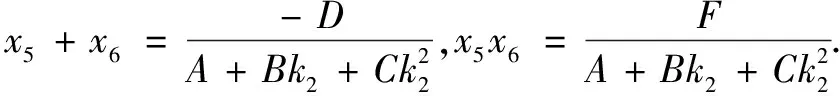
p+q

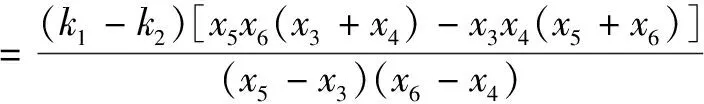
又由上可知x5x6(x3+x4)=x3x4(x5+x6),故p+q=0,即MP=MQ.

评注特别地, 在推广2中,直线MD或ME为切线,结论依然成立.

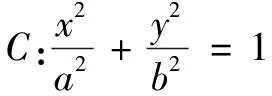
(1)求椭圆C的标准方程;

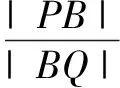
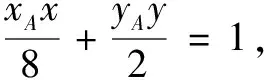
例4(2012年北京高考题)已知曲线C:(5-m)x2+(m-2)y2=8(m∈R).

(1)若曲线C是焦点在x轴上的椭圆,求m的取值范围;

(2)设m=4,曲线C与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线C交于不同的两点M,N，直线y=1与直线BM交于点G，求证:A,G,N三点共线.

解(1)略.

(2)由题知曲线C的方程为x2+2y2=8.

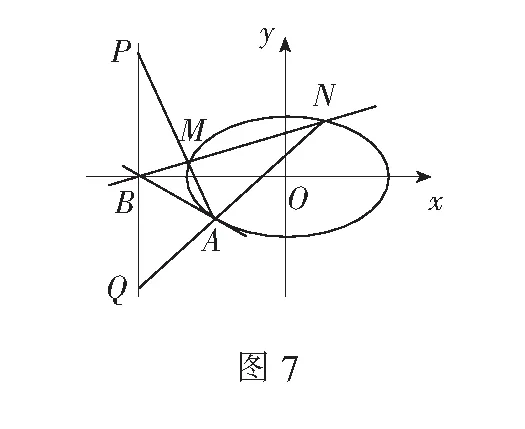
如图8，设直线y=1与椭圆相交于E,F两点,易验证DE,DF为椭圆的切线(E,F为切点).由蝴蝶定理推广2,可知DP=DQ.

在高中阶段的解析几何,传统的解法主要是靠代数关系来研究几何问题.以上研究表明在常规数学教学之中,若能对解析几何的知识进行有机的补充,既能挖掘和弥补课外有益的知识点,又能培养学生的数学核心素养,训练其综合分析与解决问题的能力,对于某些特定类型的题目起到秒解的效果.