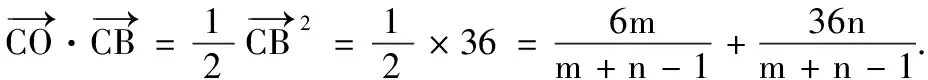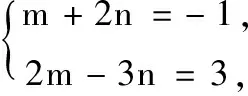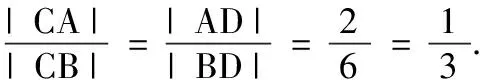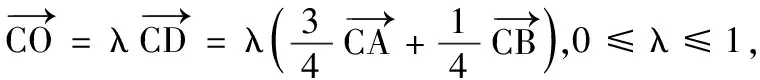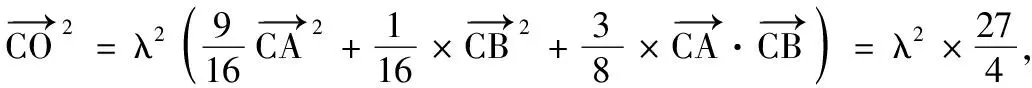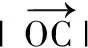高一数学测试

一、单项选择题(本大题共8小题，每小题5分，计40分)

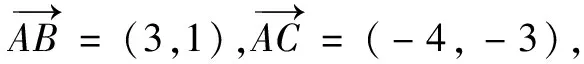
(A)(-7,-4) (B)(7,4)

(C)(-1,4) (D)(1,4)

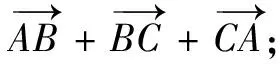
(A)1 (B)2 (C)3 (D)4

3.设a,b为平面向量,则“存在实数λ,使得a=λb”是“向量a,b共线”的( )

(A)充分而不必要条件

(B)必要而不充分条件

(C)充分必要条件

(D)既不充分也不必要条件

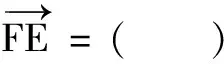
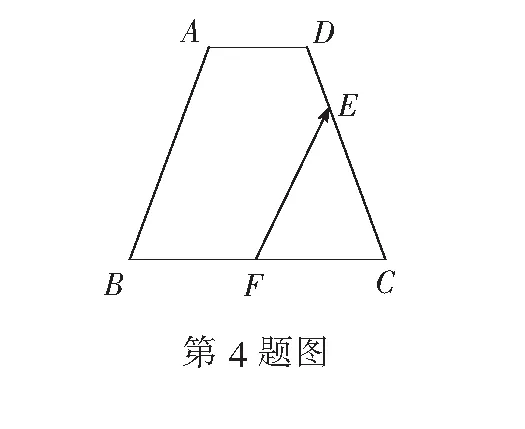
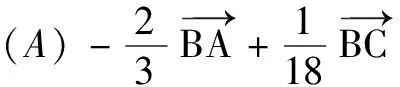
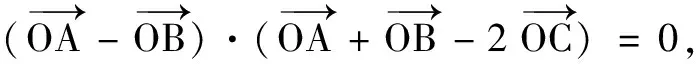
(A)钝角三角形 (B)直角三角形

(C)等腰三角形 (D)等腰直角三角形

6.已知平面向量a,b满足|a|=3,|b|=3,(a-b)⊥b,则sin=( )

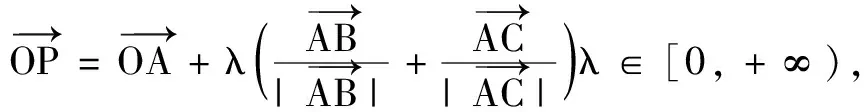
(A)外心 (B)内心

(C)重心 (D)垂心

8.已知平面向量a,b满足|b|=2,b与b-a的夹角为150°,记m=ta+(1-t)b(t∈R),则|m|的取值范围为( )

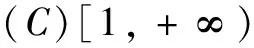
二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)

9. 已知向量a=(1,-2),b=(-1,2),则下列结论正确的是( )

(A)a∥b

(B)a与b可以作为一组基底

(C)a+b=0

(D)b与a方向相反

10.下列叙述中错误的是( )

(A)若a=b,则3a>2b

(B)向量a与向量b夹角的范围是[0,π)

(C)若a∥b,b∥c,则a∥c

11.对平面向量a,b,有( )

(A)若a和b为单位向量,则a=b

(B)若|a·b|=|a||b|,则a∥b

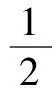
(D)已知λ,μ为实数,若λa=μb,则a与b共线

12. 下列说法中正确的是( )

(A)对于向量a,b,c,有(a·b)c=a(b·c)

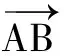
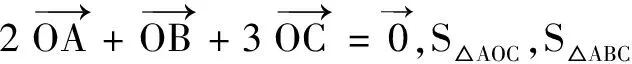
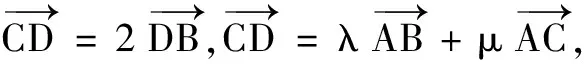
三、填空题(本大题共4小题,每题5分,计20分)

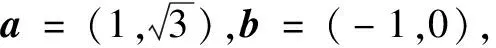
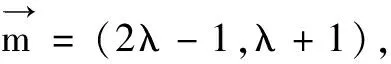
15.如果向量a与b的夹角为θ.定义:“a×b”表示一个向量,它的大小是|a||b|sinθ.若|a|=5,|b|=3,|a×b|=12,则a·b______.

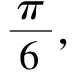
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)

17.(本小题满分10分)已知|a|=1,|b|=2,a与b的夹角是60°.试求

(1)a·b,|a+b|,a在b上的投影向量;

(2)a+b和a的夹角的余弦值.

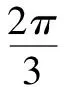
(1)求a·(a+2b)的值;

(2)若m与n的夹角是锐角,求实数t的取值范围.

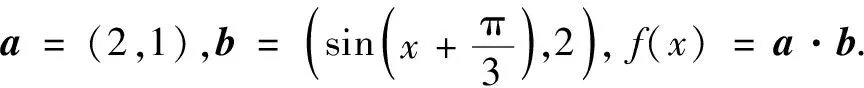
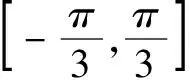
(2)求满足不等式f(x)≥3的x的集合.

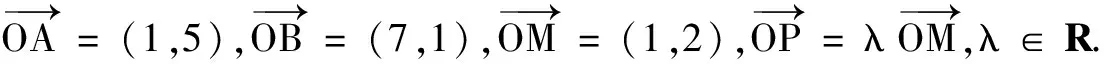
(1)当A,B,P三点共线时,求λ的值;

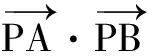
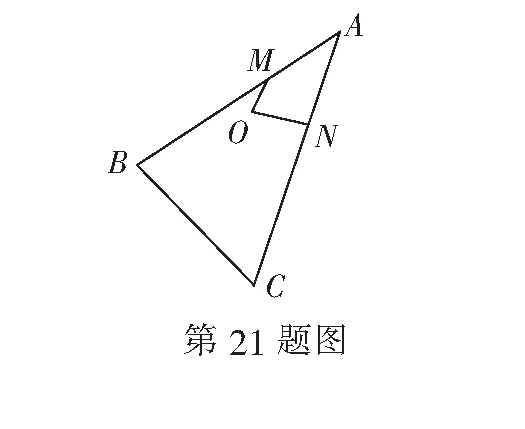
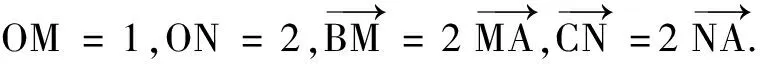
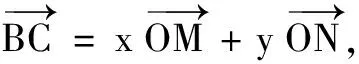
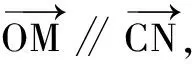
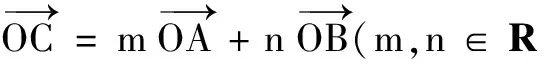
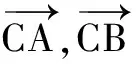
(2)若点O为∆ABC的外心,求m,n的值;

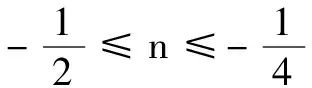
参考答案

一、单项选择题

1.A;2.B;3.A;4.B;5.C;

6.D;7.B;8.C.

二、多项选择题

9.ACD;10.ABC;11.BC;12.BCD.

三、填空题

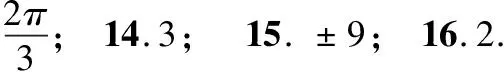
四、解答题

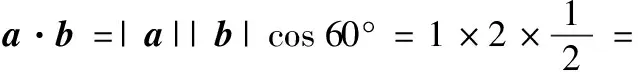
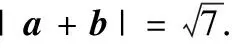
(2)因为(a+b)·a=a2+a·b=1+1=2,设a+b和a的夹角为θ,所以

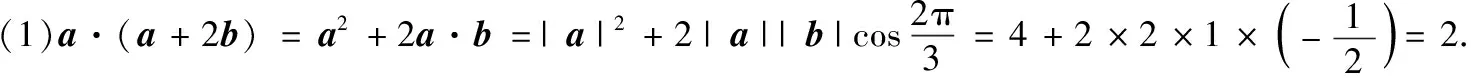
(2)因为m与n的夹角是锐角,所以m·n>0,且m与n不共线.由m·n=(2ta+7b)(a+b)=2t|a|2+(2t+7)a·b+7|b|2=6t>0,解得t>0.

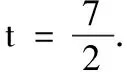
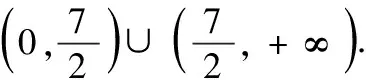
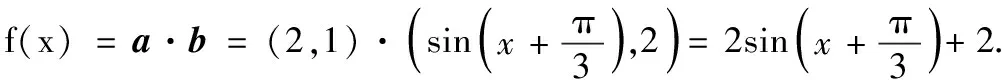
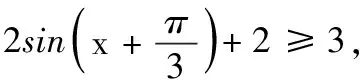
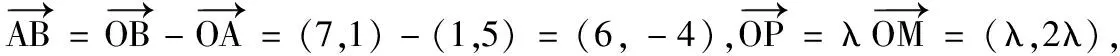
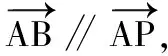
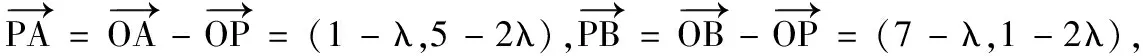
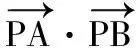
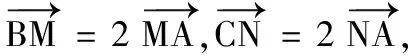
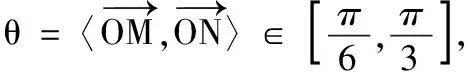
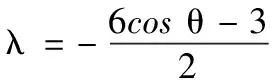
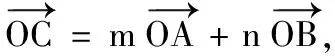
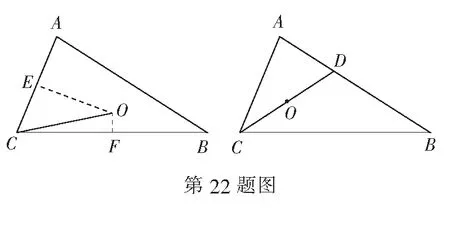
(2)如图,设CA,CB的中点分别为E,F,连结OE,OF,则OE⊥CA,OF⊥CB.