高中函数概念教学的实践与探索——“函数的概念和图象(1)”教学设计

杨 静

(江苏省扬州大学附属中学,225002)

本文以苏教版普通高中教材《数学》(必修第一册)“函数的概念和图象(1)”的教学设计与实施为例,介绍笔者落实《普通高中数学课程标准》[1]要求，培育学生数学抽象与数学建模素养的一次实践性探索.本教学设计获江苏省高中青年数学教师优秀课观摩与评比活动一等奖.

一、教学目标及重点、难点

1.教学目标

(1)通过丰富的实例,提供函数概念的背景,使学生体会函数是描述两个变量间依赖关系的重要数学模型.

(2)能用集合语言和对应关系表达函数概念,体会集合语言和对应关系在刻画函数概念中的作用.

(3)理解高中阶段函数概念的意义,理解函数符号表达与抽象定义之间的关联,了解构成函数的要素,能求简单函数的定义域.

(4)通过从实例中抽象概括函数概念的活动,积累从具体到抽象的活动经验,培育数学抽象、数学建模等核心素养.

2.教学重点与难点

重点是引导学生体会用集合语言和对应关系刻画函数概念的过程,掌握函数概念及构成函数的要素,会求简单函数的定义域.

难点是抽象概括函数的概念,理解函数抽象定义的符号表达.

二、教学过程

1. 数学情境,引出概念

情境1前段时间,扬州疫情牵动着全省乃至全国人民的心.在党和政府的关心下,在全省人民的支援下,自8月15日开始,疫情得到了切实有效的遏制.表1是8月15日到8月22日8天的每日新增新冠肺炎确诊病例数,记8月15日为第1天.

表1 8月15日—8月22日每天新增病例数据表

问题1用数学的眼光看问题,这里的天数,新增病例人数都构成了集合,你能写出这两个集合吗?

问题2这两个集合之间有关系吗?

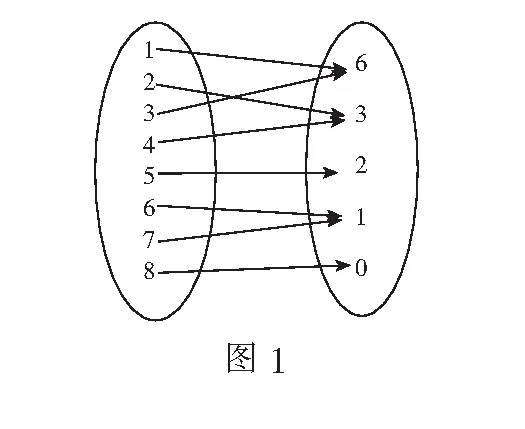
总结:天数构成的集合A与新增病例人数构成的集合B之间有如图1所示的对应关系. 以上问题告诉我们,某些集合之间可能存在某种对应关系.

设计意图引导学生以数学的眼光思考现实世界,发现集合与集合之间可能会存在对应关系,为情境2引出函数做铺垫.

情境2连淮扬镇铁路被誉为江苏高铁的金腰带.昨天我乘“复兴号”从扬州来到交通枢纽——徐州东站,假设“复兴号”高速列车加速到240 km/h后保持匀速运行10分钟.这段时间内,列车行进的路程S(单位km)与运行时间t(单位:h)的关系可以表示为S=240t.

问题3S=240t(在初中见过)表达了什么关系?

生:路程S是关于时间t的一次函数.

问题4同学们,初中还学过哪些函数?

生:一次函数、二次函数、反比例函数.

问题5你还记得初中阶段函数是怎样定义的吗?

生:每一个自变量x,都有一个y与它对应.

师:很好!下面回顾一下初中阶段函数的概念:在一个变化过程中的两个变量,记为x和y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说y是x的函数.x是自变量.

追问:为何路程S是关于时间t的一次函数?

生:对于t的每一个值,S都有唯一的值与它对应.

追问:t=1时,S的对应值是多少呢?

生:S也构成一个实数集,集合B=[0,40].

师:集合A中每一个元素t,在集合B中都有唯一的S与它对应.也就是集合A与集合B之间存在某种对应关系(如图2).这个对应关系就是S=240t.且这种对应关系可以构成一次函数.

问题6情境1中,从集合A到集合B的对应关系能构成函数吗?

生:能,集合A中每一个元素,在集合B中都有唯一的元素与它对应.

设计意图通过追问“t=1时,S=240对吗?”引导学生需考虑时间t的范围,从而给出实数集合间对应关系的表述.在对情境1是否构成函数关系的讨论中,帮助学生建立从集合之间对应关系的角度去认识函数,为用集合语言描述函数概念作出铺垫.

情境3以下是徐州市某一天24小时内的气温变化图(图3).

问题7一天的温度与时间能够成函数关系吗?

生:能,时间构成一个实数集A=[0,24],温度构成一个实数集B=[-2,9],集合A中的每一个时刻t,集合B中都有唯一的温度θ与它对应(如图4).

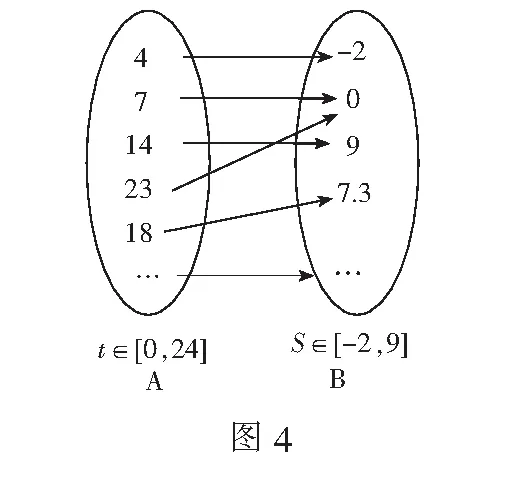
设计意图情境3很难用一个解析式表示.让学生在思维碰撞中感知变量依存关系表达的局限性,认识到进一步学习函数概念的必要性.

2.数学建构,生成概念

问题8如图5,上述3个情境中的两个变量之间的关系有何共同特点?你能尝试用集合语言和对应关系重新描述这一共性吗?你能用集合语言和对应关系重新描述函数的概念吗?

引导学生抽象概括如下关系(图6):

设计意图通过“变中求同”总结3个情境的共同特征.并从集合与对应的角度概括描述以上3个函数的本质,形成函数的概念.

函数的概念:给定两个非空的实数集合A和B,如果按照某种对应关系f,对于集合A中的每一个实数x,在集合B中都有唯一的实数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),x∈A.其中x叫作自变量,集合A叫作函数的定义域.

若A是函数y=f(x)的定义域,则对于A中的每一个x(输入值),都有一个y(输出值)与之对应.所有输出值y组成的集合{y|y=f(x),x∈A}称为函数的值域(图7).

3.数学活动,内化概念

数学活动1请同学们举一些生活中的例子,并请同桌判断是否为函数.

数学活动2请同学们判断下列对应是否为函数(图8).

分析判断对应是否构成函数的依据只有定义,只要判断是否满足定义即可.

数学活动3下列函数中哪个与函数y=x是同一个函数?

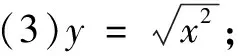
分析如果定义域、对应关系、值域均相同,则函数相同.而值域由定义域与对应关系决定,所以如果对应关系、定义域相同,那么这两个函数就是同一个函数.

问题9你认为函数定义中有哪些关键要素?

设计意图让学生理解并使用函数符号y=f(x).通过图8中④,理解值域C={y|y=f(x),x∈A}的定义,得到C⊆B的认知.

4.数学应用,巩固概念

例1判断下列对应是否为函数:

(2)x→y,这里y2=x,x∈N,y∈R.

(3)当x为有理数时,x→1;当x为无理数时,x→0.

例2求下列函数的定义域:

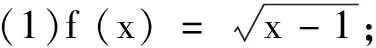
例3求下列函数的值域:

(1)f(x)=(x-1)2+1,x∈{-1,0,1,2,3};

(2)f(x)=(x-1)2+1.

设计意图函数概念形成后,通过3道例题促使学生关注函数的本质,加深对函数概念的理解.

5.自主小结,融通概念

问题10本节课,我们在初中函数概念的基础上,运用集合语言进一步完善了函数的概念,请你谈谈本节课有哪些收获?

师生共同完成表2：

表2 初高中函数概念的区别与联系

拓展阅读:函数概念的发展史.

设计意图学生通过自主小结,感悟不同阶段的函数概念的区别与联系.每一个数学概念的形成都蕴含着丰富的数学历史文化,拓展性阅读有助于学生深刻认识和理解函数概念,让学生发现函数概念还可以继续完善和扩充.