聚焦核心素养 突出运算能力

岳剑平

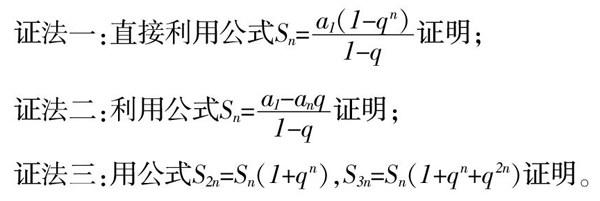
摘  要：运算能力是学生学习数学应该具备的关键能力，也是数学核心素养的重要内容，培养学生运算能力既是新课改对广大数学教师提出的根本要求，也是学生发展的内在需要。本文以高中数学教学为例，聚焦数学核心素养要求，简要分析当前高中学生数学运算存在的一般问题，重点探讨高中数学教学中如何着重培养学生数学运算能力，为促进学生数学核心素养发展奠定基础。

关键词：高中教育;数学教学;核心素养;运算能力

一、数学运算的一般问题

运算能力不是指简单地计算，其核心是“运算”，主要包括运算对象和运算规律两方面内容，从小学到高中，学生面对的数学运算对象和运算规律越来越复杂，需要解决的运算类问题也越来越多，尤其是到了高中阶段，学生不仅需要运用数学知识解题，更需要具备良好的运算能力才能确保问题正确快速得以解决。从当前高中学生运算相关问题的学习现状来看，大部分学生存在如下几方面问题：

一是审题不完善。从教学实践来看，很多学生从小学到高中，始终存在审题问题，审题不全面，对题干信息的挖掘比较片面，很难快速挖掘出题干的隐含信息，导致运算难度变大，运算不正确，最终影响解题效率和正确率。

二是基础不扎实。是否能够正确运算是基于学生是否真正理解和掌握数学基础知识的，只有掌握数学概念、定理、公式、法则等基础知识，才能灵活地、正确地运用这些数学基础知识和数学规律解决实际问题。但事实却是很多学生将这些基础知识背到滚瓜烂熟了，即使是将数学概念、定理、公式牢记于心，但也会出现运算失误，根本原因在于学生对内涵和外延理解不清，对数学公式、定理、发展理解不透彻，容易扩大或者缩小基础知识应用范围，导致运算错误。

三是运算思维不灵活。运算不仅是计算过程，也是学生对条件、问题进行分类讨论、归纳整理的过程，很多学生在运算过程中总是存在讨论不全面，分类不严谨，影响了运算效率和正确率。

四是策略选择失误。数学运算过程其实也是学生选择解题策略能力的直接体现，选择合适的解题策略，运算效率也会事半功倍，选择错误的解题策略，运算量和难度可能都会加倍。不少高中学生仍然无法正确结合问题选择合适的解题策略，比如某一问题应该运算数形结合思想还是类比推理，判断错误导致策略选择错误，最终影响运算结果。

二、聚焦核心素养，培养学生运算能力的策略

（一）重视过程教学，夯实基础知识

基础是关键，基础知识掌握是否扎实，理解是否透彻，都直接影响学生运算效率，制约学生运算能力提升。新高考大纲也对学生运算能力做出了明确界定，强调运算能力包括学生对运算条件、方向的选择能力以及运算公式应用能力和计算方面的能力。为此，在教学实践中，数学教师应重视数学概念、公式、定理、法则等基础知识教学，摒弃传统的死记硬背教学方式，引导学生自主归纳概念、推导公式、总结定理和法则，让学生成为学习的主人，真正经历知识形成过程，更透彻和全面地理解掌握这些基础知识，为学生灵活运用基础知识解决实际问题奠定基础。

在指导学生解不等式（x+2）（3-2x）>0时，就可以先从算理着手，引导学生分析算式-2x2-x+6>O和（x+2）（3-2x）>0之间的关系，让学生明白（x+2）（3-2x）>0是由-2x2-x+6>0这一算式分解而来的，由此可以发现算式是一条开口向下的抛物线，不等式的解集应该处于两解之间，再结合图形相关知识，将原不等式中的3-2x改写成-（2x-3）即可快速破题。这一过程其实就是算理的运用过程，既深化了学生对算理的理解，也提高了学生解题效率，有效避免了学生运算错误。

（二）剖析经典例题，总结运算规律

当学生掌握了基础知识并且对知识形成一定的体系后，教师还需要引导学生总结数学运算规律。因为基础知识能够有助于学生理清解题思路，但学生还无法敏锐地、灵活地解决问题。其原因就是学生对运算规律掌握不全面。鉴于此，不妨适当给学生增设经典例题，师生共同剖析经典例题，在例题磨合中总结规律，让学生真正做到具体问题具体分析，在例题中分析和琢磨运算条件、探究解题方向，总结运算规律。经过长期训练，学生掌握的运算规律更全面，在运算过程中更能灵活应对。

例如：函数f（x）=1/ln（x+1）+4-x2的定义域为（ ）

A. [-2，0]∪（0，2） B. （-1，0）∪（0，2）

C. [-2，2] D. （-1，2）

此题中，函数存在的意义是x+1>0且ln（x+1）≠0，同 时，4-x2≥0，换言之即是：x>-1且x≠0-2≤x≤2即-1

（三）巧设一题多解，培养学生多变运算思维

思维是影响能力的关键因素，良好的运算思维是高中学生学好数学这门课程应该具备的，也是提高学生运算能力的核心。在核心素养指导下，广大数学教师已经充分意识到学生思维培养的重要性，而以突出运算能力为主的数学教学也必须加强学生运算思维培养。针对此要求，建议广大数学教师适当给学生增设一些一题多解类习题，通过一题多解对比分析，促进学生对运算法则的理解，也间接培养学生概括能力、分析能力、归纳能力、解题能力，促使学生思维向多变性、灵活性、开放性、创新性发展。如下列例题，教师可重点引导学生探究多种解题方法，并且鼓励学生从众多解题方法中归纳总结最简单、效率最高，最适合自己的方法。

例题1：解不等式3<2x-3<5，此题就有多种解法。

解法一：结合绝对值定义分类讨论求解;

解法二：将原不等式转化为不等式组求解;;

解法三：利用等价命题法解题;;

解法四：利用绝对值的集合意义解题。

例题2：已知等比数列Sn的前n项和，S3，S6，S9成等差数列，求证：a2，a5，a8成等差数列。

证法一：直接利用公式Sn=证明;

证法二：利用公式Sn=证明;

证法三：用公式S2n=Sn（1+qn），S3n=Sn（1+qn+q2n）证明。

事实证明，定期给学生设置一些一题多解类例题，引导学生从一题中探索多种方法，从多种方法中总结最佳方法，不仅是对学生进行专项实战训练，更是对学生进行运算思维训练，潜移默化地培养了学生多变思维，提高了学生运算能力。

三、结语

随着课程改革的深入，核心素养已经成为指导广大数学教师开展教学活动的理论思想，以核心素养为导向的高中数学教学首先要重视学生运算能力培养，不断创新教学方法，优化教学过程，以提高学生运算能力，为学生数学核心素养发展夯基。

参考文献：

[1] 邱光云. 基于核心素养下高中数学运算能力培养的策略研究[J]. 读写算，2019（22）：120-121.

[2] 谢永清. 高中生“数学运算”素养的落地之策[J]. 当代教育与文化，2018，10（03）：81-84.

[3] 蔡述铃. 基于数学运算素养的高中数学教学模式探究[J]. 高考，2020（18）：166.

（责任编辑：莫唯然）

本论文系福建省教育科学“十四五”规划2021年度课题“高中数学学生阅读理解能力的教学研究”（课题立项批准号：FJJKZX21-020）研究成果。