小学数学创想学习的教学研究
吴静

摘要:小学数学创想学习是在小学数学学习情境下,借助合理的想象、联想等思维形式,沟通知识之间、知识和生活之间以及各学科知识之间的联系,构想出新知识、新方法的学习样态。教师要着力从环境的营造、活动的组织和评价的落实等方面实施小学数学创想学习的教学,以帮助学生激活创想意识、积累创想经验、提升创想能力。具体可以营造开放的问题情境、自由的探索氛围、多维的活动场域,让学生“做”“想”“变”;进而制订评价标准,开展多元评价,促进成果迁移。
关键词:创想学习;小学数学;学习环境;学习活动;学习评价
创想学习是在特定的学习情境下,借助丰富的想象,利用已有的经验将知识进行有意义、多向度的关联,创生出新事物形象的过程。小学数学创想学习是在小学数学学习情境下,借助合理的想象、联想等思维形式,沟通知识之间、知识和生活之间以及各学科知识之间的联系,构想出新知识、新方法的学习样态。小学数学创想学习并非为了创立一个全新的概念、定理或法则,而是对某个已有数学知识的重构和再造,其本质是数学知识的“再创造”。它具有情境性、探究性、思考性和开放性的特点。教师需要积极开发适合小学数学创想学习的系列活动,让学生像数学家一样亲历数学知识的发生、发展过程,在数学学习中成为探索者和创造者。
一、小学数学创想学习的价值
苏霍姆林斯基曾经说过:在人的内心深处都有一种根深蒂固的需要,这就是希望自己是一个发现者、研究者和探索者,而在儿童的精神世界中,这种需要则特别强烈。B.A.苏霍姆林斯基.给教师的建议[M].杜殿坤,编译.北京:教育科学出版社,1984:58。催化小学数学创想学习是基于儿童立场的教学探索和实践,不仅能尊重和释放儿童的天性,还能全方位、多角度地拓宽学习的空间,打开思维的通道,使得对知识的理解更深刻、运用更灵活,思维也更加自由且富有创造性。
(一)从被动走向主动,变革学习方式
与传统学习相比,创想学习不是把学生看作被动接收知识的容器,由教师将现有的数学结论直接灌输其中,而是在有挑战性的问题驱动下,激发学生的探究欲望,引导学生主动参与新知的建构过程。小学数学创想学习是对僵化、被动的学习发出的挑战,是学生主动获取数学知识的学习方式,能使数学学习过程不再枯燥乏味、毫无新意,而变得生动有趣、富有创意。
(二)从割裂走向关联,完善认知体系
夸美纽斯指出:人们学习的每一件事情都应该是充满联系的。弗赖登塔尔.作为教育任务的数学[M].陈昌平,唐瑞芬,等编译.上海:上海教育出版社,1995:73。数学教学的实质就是建立知识(认知)联系(体系)。然而,当下的小学数学课堂中,“只见树木,不见森林”的碎片化、散点式知识教学现象普遍存在。小学数学创想学习旨在改变知识之间割裂、数学和生活脱离的现状,通过重构某个数学知识而实现知识之间、数学和生活之间的联系,帮助学生基于整体思考,构建结构化、系统化的知识网络,从而完善已有的认知体系。
(三)从旁观走向亲历,促进深度学习
创想学习中,学生不是学习的“旁观者”,而是积极参与知识生成过程的“建构者”。皮亚杰认为,对概念或理论的真正理解意味着学生对它的再造。陶行知.陶行知全集(第4卷)[M].成都:四川教育出版社,1991:543。以数学知识“再造”为特点的小学数学创想学习,为学生深度理解知识创造了机会。学生不是被动接受知识,而是主动思考问题,通过观察、猜想、操作、验证、演绎、归纳和抽象等活动,在与同伴、老师积极的互动和对话中,亲历知识的“再造”过程。在这个过程中,学生主动发现和提出问题,创造性地分析和解决问题。因此,小学数学创想学习是启迪思考、增长智慧的深度学习。
(四)从封闭走向开放,培育创新能力
小学数学创想学习以创生新知识、新方法为目标。新知识、新方法的建构不是一步到位的,需要突破原有思维的局限,跨越思维的重重障碍,才能从旧的“此岸”到达新的“彼岸”。小学数学创想学习是培育学生创新意识和能力的重要路径。教师要基于对数学本质的深入思考和对学生思维能力的准确把握,设计开放、灵活的问题,提供充分的自由探索时间和空间,最大限度地调动学生的创造潜能和想象力,全方位打开学生的思维通道,實现对数学知识的创造性表达。
二、小学数学教学中如何催化创想学习
学生的创想学习离不开教师的引导和支持。教师要着力从环境的营造、活动的组织和评价的落实等方面实施小学数学创想学习的教学,以帮助学生激活创想意识、积累创想经验、提升创想能力。
(一)营造适宜的学习环境,激活创想意识
学习环境(包括内容情境、心理氛围、物理环境)对激发创造潜能、提升想象空间有着重要的意义。营造适宜的学习环境,能有效调节学生的学习心理,催生创想意识。
1.开放的问题情境
开放的问题情境能调动学生学习的内驱力,触发想象、成就创造。教师要设计有争议的、有适度挑战性的问题情境,引发学生的好奇心和探究欲,激活学生的创造性思维。例如,教学“圆的认识”时,教师可以先徒手画一个圆,再提供直尺、圆规、绳子、钉子、笔等工具,让学生思考如何利用不同的工具画一个标准的圆。
2.自由的探索氛围
自由的探索氛围是学生创想学习的有力保障,教师要为学生创造自由思考和表达的机会,赋予学生自主学习的权利,包括选择画图、列表、列举、推理等一种或多种解题策略的权利,选择独立思考、自主探究或同伴合作等学习方式的权利,选择语言、图形、模型等表达方式的权利,大胆阐述自己的观点、质疑他人想法的权利等。例如,教学“梯形面积计算”时,教师直接让学生利用学过的知识求出梯形面积,再组织多种方法的交流,在此基础上通过分析和比较,沟通各种方法之间的联系,进而推导出计算公式。
3.多维的活动场域
教师在创想学习的教学中,要为学生打造立体的活动时空,拓展多维的活动场域,引导学生从固定教室走向游戏室、实验室、电脑室、图书馆等专用教室,从教室走向走廊、操场、花园等室外场地,从学校走向家庭、社会,在社区、工厂、商店等场地开展学习。例如,学生认识了厘米、米等长度单位后,教师让他们测量学校长廊的长度、篮球场的长和宽等,鼓励学生灵活运用“步测”“尺测”等方法解决问题。
(二)组织丰富的学习活动,积累创想经验
丰富多样的学习活动是学生积累学习经验、培育学习能力的有效载体。教师要科学地设计和组织活动,引导学生在“做”“想”和“变”中丰厚创想经验,激发创造潜能,实现知识和方法的创建。
1.“做”中萌发创想经验
儿童的智慧在他们的指尖上。B.A.苏霍姆林斯基.给教师的建议[M].杜殿坤,编译.北京:教育科学出版社,1984:77。学生在操作学具的过程中手脑并用,常常会迸发灵感。教师要精心设计表征、游戏和实验等活动,让学生在“做”中“思”、在“做”中“创”。
在表征中“做”。数学表征是借助外在的图形、实物、语言、符号等表示知识的一种方式。它是不同的思维水平和理解能力的外在体现,其实质就是数学创造。例如,教学“11—20各数的认识”时,让学生先用1捆和1根小棒表示11,再用大小不同的石子、珠子和2根小棒等材料继续表征。实践表明,学生的想象力是不可估量的,他们大胆突破原有结构(1捆表示10根)的限制,对现有材料进行创造性运用,完成了11的个性化表征(如图1所示),实现了十进位记数法的“再创造”。
在游戏中“做”。适时引入数学游戏不仅能激发学生的学习兴趣,还有助于培养学生的求异思维。例如,教学“轴对称图形”后,设计拼图游戏,要求同桌比赛:用两副三角板拼出轴对称图形,拼出图形个数多的一方胜出。学生在游戏中深化概念理解,不断调整和改变思考路径和方向,构想出不同的轴对称图形。
在实验中“做”。数学实验是指在思维参与下,借助对材料的操作解决数学问题的一种探究活动,是培养学生创新能力的重要活动方式。例如,教学“长、正方体表面积”后,设计“用27个完全相同的小正方体搭成一个大正方体,从中拿走1个小正方体,表面积会发生变化吗?”这一问题,让学生猜想结果,然后通过实验加以验证。在实验中,学生不断地打开思路,修正和完善自己的想法,发现表面积變化的各种可能和对应的拿法:从顶点处拿,表面积不变;从棱中拿,会增加小正方体2个面的面积;从面中拿,会增加小正方体4个面的面积。
在设计中“做”。学生的灵感不仅源自已有的学习基础,还极大地依赖于生活经验。教学中,要加强数学和生活的联系,让学生根据生活需要做“小设计师”,综合运用所学的知识进行平面图、包装袋和实践活动方案等的设计,激发学生的创造潜能。例如,复习“立体图形的表面积和体积”时,可让学生给同样大小的几个酒瓶、茶杯等物体设计包装袋,要求写出1—2个设计方案,并写出思考过程。
除此之外,创编数学绘本、制作思维导图等,都能帮助学生在“做”中思考和想象,促进创想能力的发展。
2.“想”中丰厚创想经验
思考和想象是创想学习的灵魂。教师要鼓励学生在活动中大胆地“想”,通过猜想、假想和联想等活动,培育创新思维,助推数学知识的创造性表达。
以“猜想”把控思维方向。没有大胆的猜想,就没有伟大的发现。教师要尽可能创设条件,让学生凭借直觉,主动联系已有的知识和经验进行猜想,以此探寻研究的方向。例如,教学“三角形内角和”时,可以通过实验改变△ABC中∠A的大小,让学生观察并思考“随着∠A的变化,∠B和∠C会发生怎样的变化”,从而产生“3个内角的度数和是不变的”“∠A增加的角度会与∠B、∠C减少的度数抵消”“根据∠A逼近BC 边的情况,三角形内角和是180°”等猜想。
以“假想”打破思维局限。假想是为了解决问题,通过想象设定与实际情况有距离的某种状况的一种思考方式。假想能帮助学生摆脱原有思维的束缚,开拓创新思维,寻找解决问题的有效策略。例如,教学“圆的面积计算”时,由于圆的边是“曲的”,学过的平面图形的边是“直的”,学生认为其不能转化成学过的平面图形从而推导面积公式。这时,教师要鼓励学生大胆想象,假定能转化成某个“直边图形”,再引导学生通过尝试将圆等分成2份、4份、8份、16份,感受边由“曲”变“直”的变化趋势,并不断细分,从而推导出圆的面积公式。
以“联想”拓宽思维路径。联想是由某个数学事实、现象想起其他相关的数学知识或生活现象的过程。联想有助于思维的发散,能让学生多角度、多方面地观察和思考数学问题,寻找数学知识之间、数学与生活之间的关联,进而获得解决问题的灵感。例如,教学“减法的性质”时,引导学生联系生活中的购物经验,解释性质,促进理解;教学“圆柱的体积”时,引导学生联想长、正方体体积和圆面积公式的推导方法,进行公式推导,再联想其他立体图形,进行公式迁移。
3. “变”中提升创想经验
通过变化问题的信息、结构、形式等让学生建构知识,能够充实学生的思维路径,提升学生的创想学习经验。在教学中,教师要经常采用一题多变的策略,以“变”引发学生“创”。
变“做题”为“编题”。教师要在学生理解基本知识和方法的基础上,设计开放性的问题,通过减少限制条件、补充问题等方式为学生灵活解题创造条件。例如,组织乘法运算律练习时,可设计32×()、32×2.5+()○()等问题,让学生先补充问题,再简便计算;教学“轴对称图形”后,可设计“在格子图上画出轴对称图形的另一半”的练习,让学生自行变化对称轴的位置构造图形;教学整数、小数、分数四则运算时,可让学生创编相关的实际问题,等等。
变“给定”为“重构”。实践表明,非良构问题有助于发展学生的创新能力。教师要适时对知识进行“解构”,引导学生对原始的非结构化材料进行“重构”。例如,教学解决实际问题时,为学生提供一组信息,要求学生选择相关条件提出问题;教学图形的认识内容时,让学生选择小棒拼搭图形,探索并发现图形的特征;教学度量内容时,让学生根据测量单位重构尺子、量角器等测量工具;教学统计图表时,启发学生基于实际问题进行图表建构。
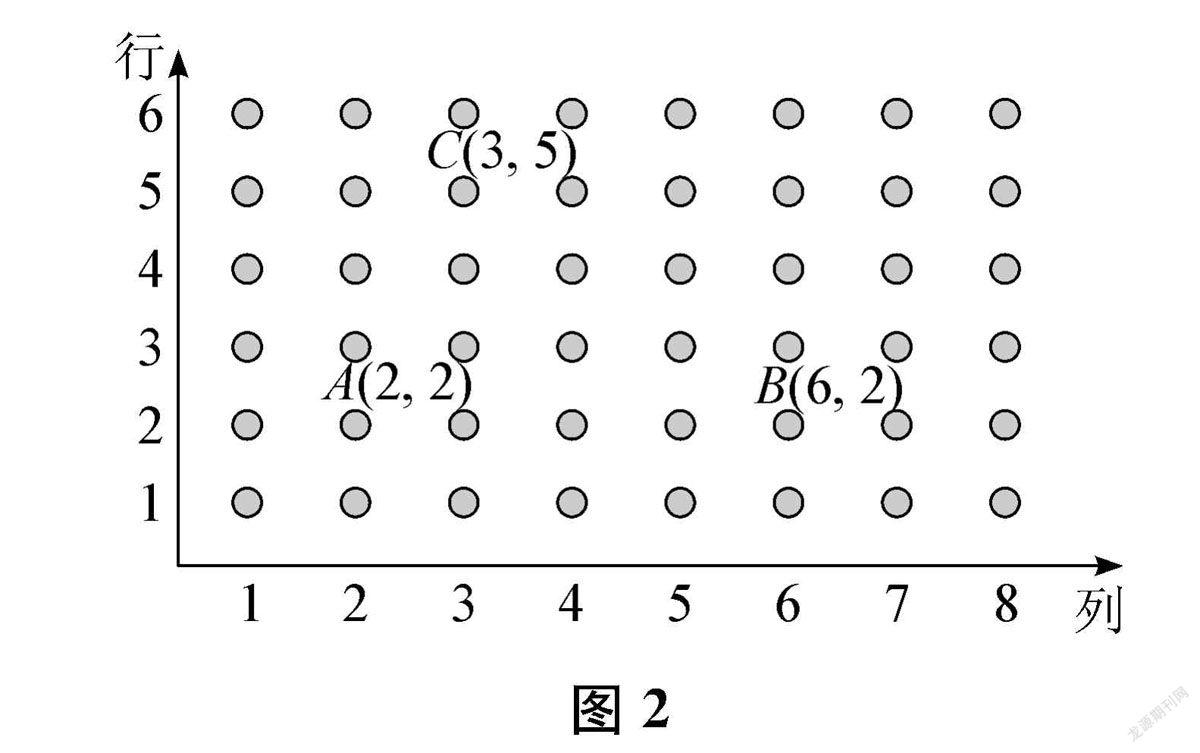
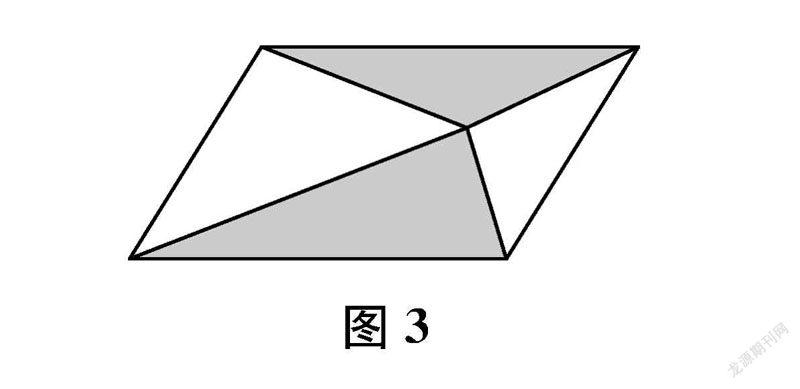
变“唯一”为“多解”。单一的问题形式容易使学生产生思维定式。而经常变化问题的形式,包括设计逆向思考的问题,能提高学生思维的灵活性。例如,教学“用数对确定位置”时,可以让学生在图2中根据梯形ABCD已知顶点A、B、C的位置(数对)找未知顶点D的位置(数对),在这一过程中不断改变思维视角;教学“平行四边形面积”时,可以让学生设计和图3中阴影部分面积相等的图形,培养学生思维的灵活性。
(三)落实科学的学习评价,提升创想能力
以学生为主体,让学生参与活动(而非简单听讲)的教学,本质上都是基于评价的教学,即以(对学生)学(的评价)定(教师的)教。在创想学习的教学中,教师要组织创想学习活动评价,帮助学改进和优化学习方式,进而提高创想学习能力。
1.制订评价标准
制订科学的评价标准是衡量创想学习成效的基础,也是助推创想能力提升的关键。教师要正确认识评价的意义,立足学生创想能力的发展,尊重学生的个体差异,编制科学的评价细则。
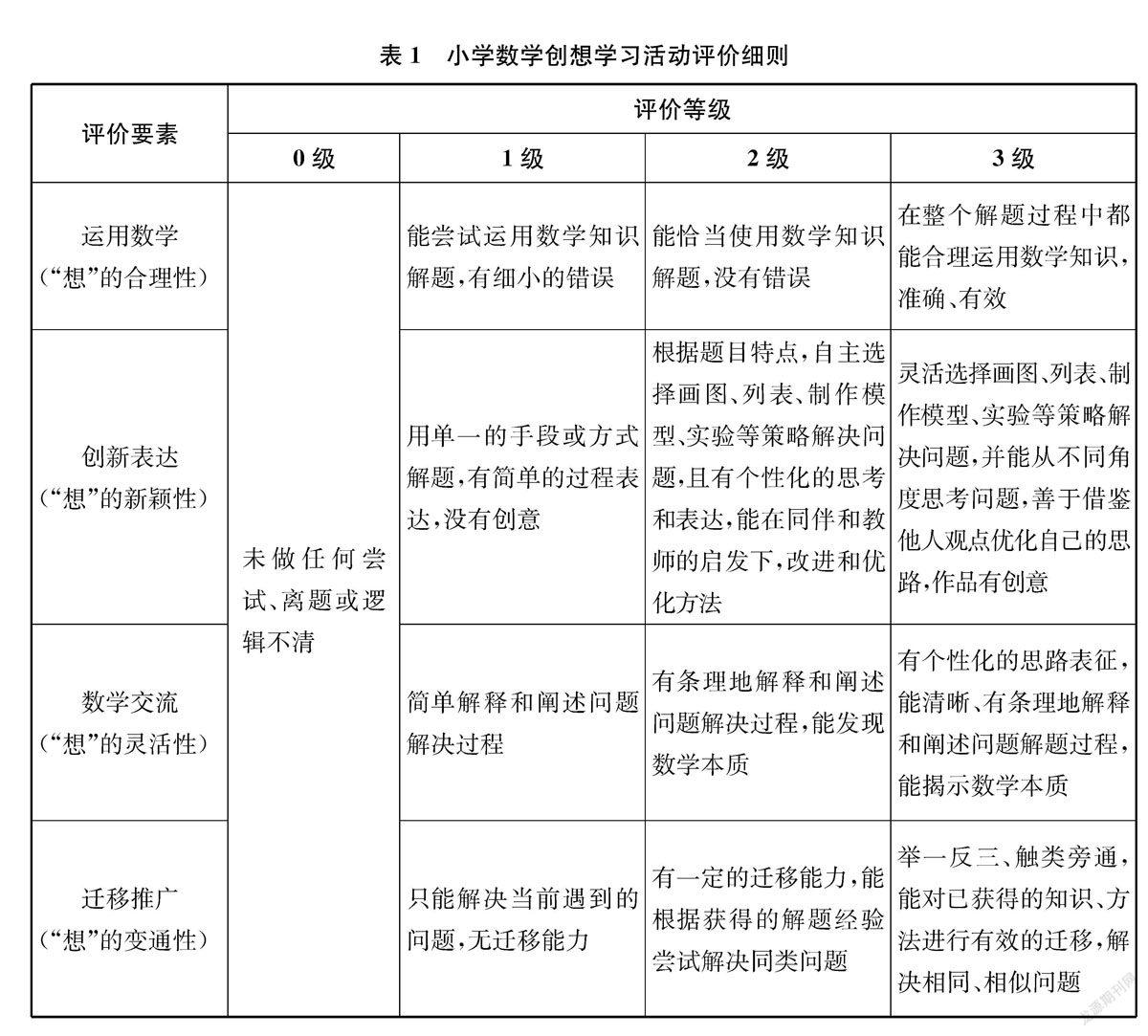
我们基于运用数学、创新表达、数学交流和迁移推广四个要素,制订了小学数学创想学习活动评价细则(如下页表1所示),旨在全面展示学生“想”的过程,从“想”的合理性、新颖性、灵活性和变通性四个维度,考查学生的创想能力,以此彰显创想学习的本质。4个等级的指标设置,进一步明晰了创想的内容和要求,为学生的创想学习活动指引了方向。例如,让学生在格子图上画一个面积为8平方厘米的正方形后,组织学生对每个作品进行评价,没有画出的为0级,画出正方形但面积不符合要求的为1级,用尝试法画出正方形的为2级,先画出16平方厘米的正方形再连接各边的中点画出的为3级。
2.开展多元评价
运用标准评价创想学习活动时,教师要坚持“为发展而评价”的原則,组织多主体、多层次、多方式的评价,从而促进学生理解力、思辨力和创造力的全面提升。
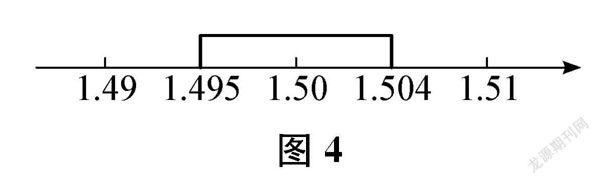
例如,在学生解答“一个三位小数,用四舍五入法保留两位小数,近似数是1.50,这个三位小数最大是多少?最小是多少?”后,教师呈现多种解题方法,包括试误法(先猜想可能正确的数,再一个一个检验)、反向思考法(□.□□□≈1.50)和直观法(如下页图4所示)等,组织两轮评价。第一轮,让学生通过观察、分析和比较,对他人和自己的作品作出评价,发现和鉴别各种方法的价值。比如,试误法比较原始、耗时较长且有风险;反向思考法虽能变“逆向”思考为“顺向”思考,但要有一般化表达的能力;画图法直观、便于理解,但要对数序有清楚的认识……在此基础上,不断优化和完善原有方案,形成高质量的作品。第二轮,让学生就先后两次的作品进行再评价,通过对比和反思,进一步加深对新方法的理解。
3. 促进成果迁移
能将新知识和方法灵活迁移至新情境,是检验学生创想学习能力的最有效的方法之一。在创想学习活动的最后环节,教师要引导学生主动进行知识迁移。这既是教学活动,也是评价活动。
例如,在学生学会用“积的变化规律”计算“小数乘小数”后,可以让学生解释“乘数末尾有0的整数乘法”“小数乘整数”的计算原理,还可以让学生简算“3.2×1.2+32×0.88”。如果学生能够灵活运用所学知识解决相关问题,证明创想学习活动的设计是有效果的、有价值的。

