精心设计，有效提升

严萍

[摘  要] 课堂练习贯穿于数学课堂教学的全过程，是激发学生学习的积极性和提升学生数学能力与素养的有效途径. 文章结合笔者自身的教学实践，提出了探究性练习、针对性练习、挑战性练习、系统性练习、递进性练习这5种练习形式，以期通过有效练习提升学生的学习效率和数学素养.

[关键词] 课堂练习;提升;数学素养

随着新课程改革的深化，在数学课堂上我们感受到了前所未有的“热闹”，一些教师为了追随新课程理念的步伐，整节课下来引导学生“再创造”出一个公式、法则，却连基本的练习都没有;还有一些教师整节课实施了互动性教学，学生看似学得有模有样，课堂看似热闹非凡，但当我们仔细审视这些看似“繁荣”的背后，不难发现其存在一些问题，尤其是到了考试时，不少学生无从下手，学生的学习效率得不到保证.

课堂练习作为一种有目的的训练活动，几乎贯穿于教学的全过程，要想提升学习的学习效率，就需要加强课堂练习的科学性. 那么，该如何操作呢？笔者认为，需要从教学内容出发，设计出贴合学生实际，具有思考价值，基于学生思维的最近发展区的问题，才能有效地提升学生的学习效率. 文章结合笔者自身的教学实践来谈谈课堂练习设计的一些尝试.

探究性练习——增强探究能力

培养学生的自主探究能力是新课改推进下的一大重要课题，随着新教材、新理念和新教法的有效促进，越发凸显以科学探究为依托的教学模式. 那么在课堂练习中又该如何加以培养呢？笔者认同，教师在课堂练习设计中应精设反映知识探究过程的问题，让学生的思维有序地融入探究活动，体会成功的喜悦和探究的价值，逐步增强探究能力[1].

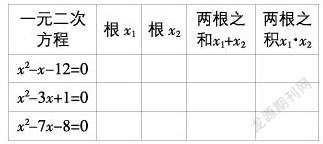
例如，在探究一元二次方程的根与系数的关系时，教师可以有意识地设计如下练习，引领学生的深度探究：

题1：填一填.

题2：猜一猜.

根据上表，猜想：若关于x的一元二次方程x2+mx+n=0（m，n均为常数）的两根是x，x，则x+x，x·x与系数m，n有何关系？

题3：说一说.

请根据求根公式探索任意一元二次方程ax2+bx+c=0（a≠0）的两根与系数a，b，c有何关系. 说出你的猜想，并说明理由.

就这样，通过探究性练习，让学生去观察、去比较、去猜想、去分析、去发现、去验证，在探究中发展，在探究中创新，在探究中进取，很好地培育探究能力.

针对性练习——领悟知识本质

课堂练习应教材、学生双管齐下进行设计，保证其针对性. 不仅需要考虑具体学情，做到不拔高、不降低、不脱离实际、不脱离理解限度，而且要重视重难点和关键点，尤其是对于一些易错点，需要通过反复练习加以强化，使学生在比较中发现知识的本质，掌握新知的重难点，从而进一步完善知识结构.

例如，教学“平方差公式”时，在师生共同“再创造”公式（a±b）2=a2±2ab+b2后，教师抛出了几道口算练习和笔算练习. 在学生练习时，教师适时巡视，很快发现了学生的易错处，从而有意识地抛出了以下练习：

题4：请填写下表，并说说你的发现.

由于练习是从学生的易错处展开的，针对性强，学生容易进入探究性学习的状态，并随着教师的设问深入探究，从而获得深刻的认识. 在一步步的练习下，找出出错根源，获得深刻理解. 此时，学生的学习情绪高涨，这种作业可以深化认识，让学生学习效率的提升进一步落实.

挑战性练习——孕育创新思维

练习设计需要充分调动学生的积极性，才能让学生主动地自主探究，而不是机械被动地完成. 愛挑战是学生的天性，作业的挑战性能够提升学生完成作业的积极性，因此教师需要适时抛出一些具有挑战性的练习，如“一题多解”“一题多变”等变式练习，通过练习孕育创新思维. 当然，在学生练习中，教师应充分尊重学生，留足思考和探究的时间和空间，充分鼓励创新，最终提升他们的数学素养.

例如，教学“四边形”时，教师可以设计如下练习：

题5：依次连接四边形的各边中点，可以得出一个什么四边形？

变式1：依次连接矩形的各边中点，可以得出一个什么四边形？

变式2：依次连接菱形的各边中点，可以得出一个什么四边形？

变式3：依次连接正方形的各边中点，可以得出一个什么四边形？

变式4：依次连接等腰梯形的各边中点，可以得出一个什么四边形？

随着学生年龄的逐步增长和学段的逐级提升，学习难度也随之增加，学习兴趣却不增反减，一些学生开始出现了学习困难的现象. 变式教学是激发学生学习主动性的有效手段，可以在促进学生积极思考时激活数学思维，调动其内在的智力活动，促进对知识的深度理解. 在本节课的学习中，由于有了变式练习的引导，学生兴趣大增，学习效果较好，在独立思考后展开了火热的讨论模式，即使下课铃响了仍在争辩，后来讨论不得不从课堂延伸到课后，因此学习效率是可想而知的.

系统性练习——有效深化认识

数学知识不是孤立存在的，都是存在于知识系统下的，所以课堂练习设计中，教师应通过少而精的系统性练习，将已学或将学的知识点巧妙串联，引领学生的思维，使得学生通过这样的课堂练习，有效深化认识，获得某一方面的系统知识[2].

例如，教学“函数的应用”时，教师可以抛出如下练习：

题6：图1是二次函数y=ax2+bx+c（a≠0）的图像，请在观察图像后回答以下问题.

（1）试写出方程ax2+bx+c=0的两个根;

（2）试写出不等式ax2+bx+c>0的解集;

（3）试写出方程ax2+bx+c=-6的实数根;

（4）试写出方程ax2+bx+c=2的实数根;

（5）试写出方程ax2+bx+c=3的实数根;

（6）设方程ax2+bx+c=k有两个不等实数根，试求出k的取值范围.

我们设计练习时需要在知识网络的构建上多做文章，让学生通过一道练习题将已学知识连成线、织成网，从而使得知识的应用价值和智力价值都能发挥出来，进而实现练有所获、学有所得. 在本例中，教师深钻教材，设计出了这样一组覆盖面大且具有代表性的课堂练习，有效地归纳了二次函数与方程的性质，让学生充分参与、注重创新，较好地体现了“优效练习”的价值追求.

递进性练习——促进共同发展

学生都是生动而独立的个体，每个学生在思维水平、学习习惯、个性品质上都表现出了不同的情形. 教师要想在课堂练习中关注到每个学生，就需要遵循循序渐进的规律，设计递进性练习，让每个学生都有“题”可做，促进其共同发展.

例如，若点（x，y），（x，y）在反比例函数y=的图像上，试判断y，y的大小关系. 这道练习题对于一些学生来说有些难度，尤其是对于一些学困生而言，他们常常会由于思维定式而无法全面作答. 因此，为了分化难点，促进理解，教师可以进行如下改编：

练习1：若点（2，y），（4，y）在反比例函数y=的图像上，请利用两种不同的方法来判断y，y的大小关系.

练习2：若点（x，y），（x，y）在反比例函数y=的图像上，且0<x<x，试判断y，y的大小关系.

练习3：若点（x，y），（x，y）在反比例函数y=的图像上，且x<0<x，试判断y，y的大小关系.

有效练习的“效”并非低投入时间，而是要科学、合理、智慧地投入时间，才能从真正意义上实现有效练习. 在本例中，正是由于有了以上层层递进的追问，才能为大部分学生提供思维方向，而不是在原题中绞尽脑汁地思考或教师一遍遍地讲解. 这样有效的练习设计，才能拓宽学生的解题思路，培养他们的解题能力.

总之，教师需要深钻教材，精心设计课堂练习，通过练习来激发学生学习的积极性，发展他们的个性，提升他们的数学能力与素养，从而为新课标下的数学学习增添魅力[3]. 課堂练习的设计是一个充满艺术的课题，需要在实践中不断反思、不断总结，努力使课堂练习成为课堂教学的一道亮丽的风景线.

参考文献：

[1]张立英. 优化数学课堂练习设计的探索与实践[J]. 课程教育研究，2015（06）：194-195.

[2]张华. 例谈课堂练习优化设计的原则[J]. 数学教学通讯，2015（16）：41-42.

[3]李敏华. 数学课堂练习优化设计探究[J]. 福建基础教育研究，2016（03）：108-109.

3299501908244