立足数学教学培养创新意识

庄步波

[摘  要] 创新意识体现的是一个国家和民族的创新能力水平，它对推动社会进步与人口素质的整体提升具有重要影响. 培养创新意识以帮助学生更好地获得新知，提升学生的数学核心素养，为学生的可持续发展提供保障. 其培养策略有：创设问题情境，激发学习兴趣;高效变式训练，拓展数学思维;开展实践活动，形成创新意识.

[关键词] 创新意识;情境;实践活动

创新是指在特定的环境下，对現有事物或知识进行改进或创造出新事物. 创新意识是实现创造前的动机或意向，它以一种设想或愿望的形式呈现. 受生活环境、认知水平、情感体验与文化素养等综合因素的影响，每个人的创新意识与创新能力水平都有所差别. 为了适应时代的发展，培养学生的创新意识是当下乃至未来很长一段时间教育的重要任务之一.

培养创新意识的意义

1. 帮助学生更好地获取新知

我们处在信息爆炸的时代，此时初中数学知识的整合、选择与转化等成了课堂教学的重中之重. 学生不再被知识牵着鼻子走，需自主地接触并掌握迁移性强、涉及面广、概括程度高的数学知识，其中有很多内容并非三言两语就能让学生接受，而需通过知识的再创造与建构才能获得. 这就需要学生拥有良好的创新意识，来实现知识的求异性，建构新知.

2. 提升学生的数学核心素养

核心素养是新课标大力倡导的内容之一. 创新意识与能力体现了一个人的综合素养与水平，核心素养一般体现在综合化的学科知识、深厚的文化底蕴与不断进取的精神等层面. 杜威提出：“创新意识体现的是学习者的人格与思想认识，与人类的生理、心理、智力和思想等诸多方面的因素有关，它的形成可丰富学习者的综合素养. ”[1]可见，创新意识是提升学生数学核心素养的基本前提.

3. 学生可持续性发展的保障

随着教育改革的不断推进，当代的教育更趋向于素质教育的方向，所有学科的教育模式都由阶段性的教育模式转变为终身可持续性发展的教育模式. 学习不再是为了应付当下的中考、高考那么简单，而是人类赖以生存与发展的必经阶段. 随着知识的膨胀与陈旧周期的短缩，中学生创新意识的培养迫在眉睫. 一旦形成良好的创新意识，学生就能自主地完善各项能力与知识结构，为其适应社会与终身可持续性发展奠定基础.

创新意识的培养策略

1. 创设问题情境，引发学习兴趣

学生是课堂的主人，是教学活动的主体. 良好的问题情境可引发学生的学习兴趣，而强烈的兴趣又可驱动学生萌生出创新意识. 情境创设以关注学生的个性特征，遵循学生认知发展的规律，培养学生的思维品质为着手点，用问题引导学生，驱动学生的学习动机，产生学习行为.

案例1  “二元一次方程组”的教学

这是基于一元一次方程与二元一次方程之上的一个内容，在生活中的应用十分广泛. 但学生在学习时，一不小心就陷入枯燥、抽象的旋涡中不可自拔. 为此，笔者创设了一个与学生生活息息相关的问题情境，以吸引学生的注意力，让学生对此章节内容产生探究的热情.

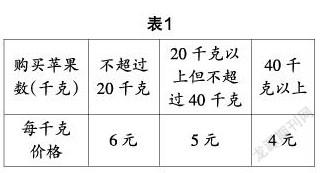
情境创设：期中考试结束，老师准备购买一些苹果来奖励近期学习有所进步的同学. 班长与生活委员两人先后去水果超市购买苹果，一共花掉264元. 超市呈现的苹果价格见表1. 两次一共买了50 kg的苹果，第二次比第一次买得多，他们两次分别买了多少千克的苹果？

这个问题难住了大部分学生，个个抓耳挠腮，讨论开来. 可见此问题的提出成功地吸引了学生的注意力，以问生趣、思中探趣的课堂导入成功地营造出良好的教学氛围，激发了学生的探究欲望.

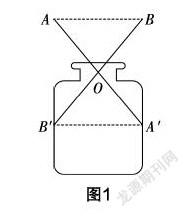
学生带着问题进行课堂学习，在对新知有了一定认识后，回过头来再解决这个问题，此时他们已经胸有成竹了. 设第一次购买了x kg的苹果，第二次购买了y kg的苹果. 由题意可确定0

《义务教育数学课程标准》提出：“数学是我们劳动、生活与学习不可或缺的一项工具，它可帮助我们进行数据的处理、证明与推理等. ”[2]这句话凸显了数学与生活的密切联系. 本题，我们从学生的生活实际出发，创设学生熟悉的生活情境，让学生在购买苹果的情境中感知实际生活问题，体验数学学科独有的魅力，为创新意识的形成奠定基础.

2. 高效变式训练，拓展数学思维

初中数学教材中有大量的例题，这些例题基本都是以定理、公式等为核心，经过精心编排而来的. 这些典型题虽然难度小，但是含有丰富的内涵与典型的数学思想和解题方法. 想要培养学生的创新意识，教师可以这些经典例题为知识迁移的桥梁，通过一题多解、补充条件或变式训练等方式开拓学生的视野，丰富学生的思维，达到以一通百的目的[3].

案例2  “二次函数”的教学

原题：已知点A，B，C分别为某二次函数上的点，这三点的坐标分别为A（-3，0），B（1，0），C（0，-3），求该函数的解析式.

变式1：已知一次函数y=-x-3的图像与x轴和y轴分别交于点A和C，某二次函数图像也经过A，C两点，同时还经过点B（1，0），请写出该二次函数的解析式.

变式2：已知点B（1，0）与点C（0，-3）是抛物线上的两点，且该抛物线的对称轴为直线x=-1，则该抛物线的解析式是什么？

变式3：已知点（1，0）是某一次函数图像上的一点，该图像与y轴的截距为-1，某二次函数图像与它相交于点A（1，m）与点B（n，4），此二次函数的对称轴为直线x=2，求出这两个函数的解析式.

这一组变式训练都需利用三点法来建立方程组从而解决问题，多题一解的变式训练不仅巩固了学生对二次函数的理解与掌握程度，还开拓了学生的思维，让学生学会在繁杂的问题中寻求问题的本质，有效地增强了学生的变通能力，也激发了学生的创新意识.

3. 开展实践活动，形成创新意识

数学教学不仅仅是书面知识的教学，还包括对数学现象的感知与感悟. 实践活动的开展能有效地增强学生的实际应用意识，为创新意识的形成打下良好的根基. 《义务教育数学课程标准》提出：“实践活动不能以记录与模仿为主，而应鼓励学生在亲自动手实践中探索数学的内涵，以形成自主探索意识与合作交流行为.”[4]因此，实践活动的开展应以师生、生生合作，互惠学习为主.

案例3  “测量圆柱体内径”的教学

生活中随处可见下半部分是圆柱体的饮料瓶，要求学生用学过的数学知识来测量圆柱体内径.

活动准备：长度相等的两根木条、大头针、直尺等.

活动方法：用大头针将两根木条的中间固定在一起，伸入瓶内后展开如图1，只要测量出AB的距离，就可根据全等三角形的性质获得A′B′的长度，很显然，A′B′的长度就是这个圆柱的内径.

在学生以这种方法测量成功后，教师提出：请大家开动脑筋，想出其他测量方法，分组讨论并展示.

学生对这个探究充满了兴趣，有的组用装水法，通过测量水面的宽度来获得瓶子的内径;有的组同样使用木条，利用相似三角形的性质进行测量;还有的组提出用垂径定理进行测量等. 学生在积极的互动中获得多种测量方法，笔者不禁也被学生的智慧所折服，创新意识在各种方法的呈现中自然形成.

伽利略认为：“科学的进步是在思维角度的不断变化中实现的. ”常新、善变的课堂是培养创新思意识的关键. 作为教师，应在思想上认识到创新意识的培养是一个长期且复杂的工程，这就需要我们跟上时代的步伐，不断地革新教育理念，在积极探索中培养出更多的现代化创新人才.

参考文献：

[1]杜威. 哲学的改造[M]. 张颖，译. 北京：商务印书馆，2004.

[2][4]中华人民共和国教育部. 义务教育数学课程标准（2011年版）[S]. 北京：北京师范大学出版社，2012.

[3]任伟芳，偶伟国，龚辉，等. “工具性理解”“关系性理解”和“创新性理解”[J]. 数学教育学报. 2014，23（04）：69-73.

3213501908262