探索思路构建,撬动思维大门
黄素兰


[摘 要] 解题教学要关注学情,以学生的思维能力为基础,引导学生探究问题,串联条件,构建思路. 中考几何压轴题常在教材知识点交汇处命题,把握图形特点,逐步拆分构建,即可达成解题目的. 解题教学中要关注学生思维,注重探究体验. 文章探究了一道几何综合题的构建过程,并提出相应的教学建议.
[关键词] 几何;动态;模型;三角函数;过程
解题教学的重点是培养学生的思维,让学生善于解题. 但解题不在于多,而在于精,要通过解题使学生深刻理解概念,扎实基础,从而灵活应对千变万化的问题. 下面以一道几何压轴题为例,关注学生思维,探究解题过程,构建解题思路.
问题呈现
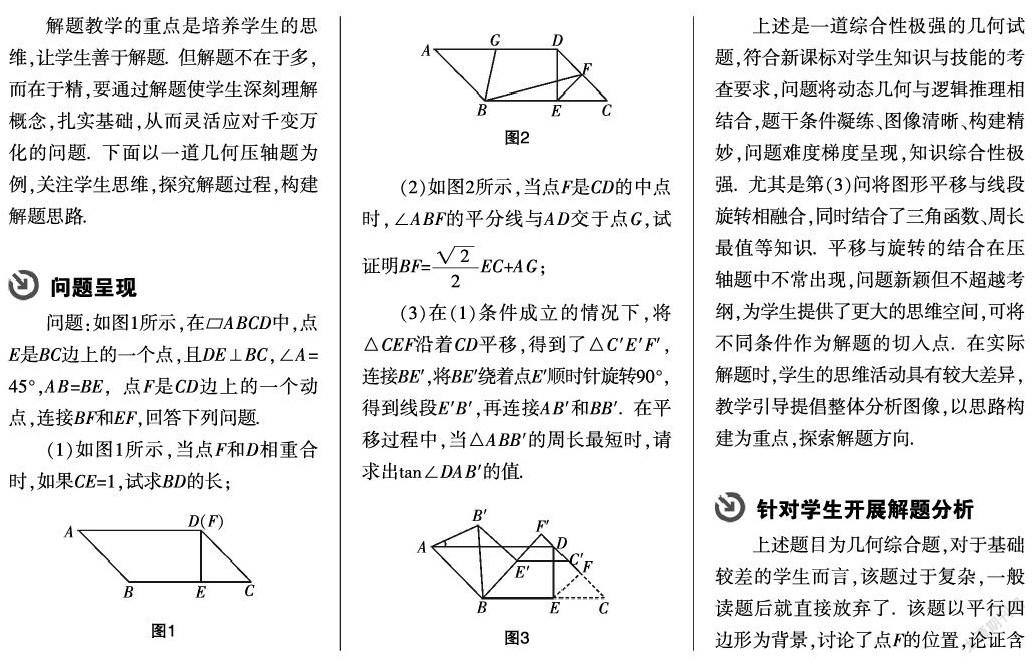
问题:如图1所示,在?荀ABCD中,点E是BC边上的一个点,且DE⊥BC,∠A=45°,AB=BE,点F是CD边上的一个动点,连接BF和EF,回答下列问题.
(1)如图1所示,当点F和D相重合时,如果CE=1,试求BD的长;
(2)如图2所示,当点F是CD的中点时,∠ABF的平分线与AD交于点G,试证明BF=EC+AG;
(3)在(1)条件成立的情况下,将△CEF沿着CD平移,得到了△C′E′F′,连接BE′,将BE′绕着点E′顺时针旋转90°,得到线段E′B′,再连接AB′和BB′. 在平移过程中,当△ABB′的周长最短时,请求出tan∠DAB′的值.
上述是一道综合性极强的几何试题,符合新课标对学生知识与技能的考查要求,问题将动态几何与逻辑推理相结合,题干条件凝练、图像清晰、构建精妙,问题难度梯度呈现,知识综合性极强. 尤其是第(3)问将图形平移与线段旋转相融合,同时结合了三角函数、周长最值等知识. 平移与旋转的结合在压轴题中不常出现,问题新颖但不超越考纲,为学生提供了更大的思维空间,可将不同条件作为解题的切入点. 在实际解题时,学生的思维活动具有较大差异,教学引导提倡整体分析图像,以思路构建为重点,探索解题方向.
针对学生开展解题分析
上述题目为几何综合题,对于基础较差的学生而言,该题过于复杂,一般读题后就直接放弃了. 该题以平行四边形为背景,讨论了点F的位置,论证含有系数的线段和差关系;引入动态图形,分析三角函数的构建. 对于基础一般的学生而言,若不能把握线段系数的特殊性,构造等腰直角三角形,运用“瓜豆原理”分析動点轨迹,则很难转化条件,也无法将条件与几何相似或全等联系起来. 因此,问题探究要注重两点:一是注重破题关键点的分析;二是注重条件转化、思路构建.
1. 第(1)问的解题分析
在第(1)问中,点F与点D相重合,结合DE⊥BC可知△DBE为直角三角形,借助勾股定理和平行四边形的性质即可求出BD的长,问题较为简单.
确定线段推导的起点极为重要,∠A=45°,则△DEC为等腰直角三角形,故DE=EC=1,可推知DC=AB=BE=. 在Rt△DEB中,DE=1,BE=,由勾股定理可得BD=,同时整个图形中的线段长度如图4所示.
教学中,教师要引导学生关注该图形中的两大特性:一是直角三角形特性——勾股定理;二是平行四边形特性——对边相等. 在几何特性的基础上开展线段关系的推导,对于其中的角度条件,可引导学生从几何特性和三角函数的视角来发掘. 对于图形线段的推导问题,建议采用上述直观呈现的方式,将对应线段标注在图中,有助于线段关系链的构建.
2. 第(2)问的解题分析
在第(2)问中,点F为CD的中点,并且∠ABF的平分线为BG,要求论证BF=EC+AG,属于含有系数的线段和差问题. 其中,系数提升了问题的难度,也为后续的图形构造提供了思路. 一些学生对系数值理解不到位,同时对含系数的线段和差关系的转化策略也掌握得不牢固,于是无法灵活地构造图形,也就无法消除系数,将其转化为常规的线段和差关系.
根据该系数,自然可以联想到构造等腰直角三角形,结合题干条件将其转化为EF或FC或DF即可. 线段和差的处理方式通常为构造全等三角形,拼接转化线段,故解题时可构造全等的等腰直角三角形来转化含系数的线段. 后续分析AB=BE,∠A=45°,故可考虑以BE为一边来构造与△ABG全等的三角形. 由于∠FEC=45°,延长FE至点H,使得EH=AG,则△ABG≌△EBH,再进一步证明FB=FH即可,具体过程如下.
延长FE至点H,使得∠GBH=135°,如图5所示. 结合平行四边形的性质可推知∠ABC=135°,故∠GBH=∠ABC,即∠ABG=∠EBH. 又知DE⊥EC,∠C=45°,故△DEC为等腰直角三角形. 点F为DC的中点,则EF⊥CF,EF=CF,故∠FEC=∠BEH=45°,EF=EC. 进一步可证△ABG≌△EBH,则可推知∠H=∠AGB=∠EBG. 又知∠ABF的平分线为BG,所以∠ABG=∠FBG. 所以∠FBG=∠EBH,从而可推知∠EBG=∠FBH,即∠H=∠FBH. 所以FB=FH=EF+EH=EC+AG.
另解 对于本题,也可以AB为边来构造与△BEF全等的三角形,后续结合平行四边形的性质可推出△HBG为等腰三角形,根据线段和差及等腰直角三角形的结论也可证明,具体如下.
延长DA至点H,使得AH=EF,再连接BH,如图6所示. 易证∠BEF=∠BAH=135°,又知AH=EF,BA=BE,则△ABH≌△EBF,所以BH=BF,∠ABH=∠EBF. 由于∠ABF的平分线为BG,所以∠ABG=∠FBG,可推知∠HBG=∠EBG. 因为AD∥BC,所以∠HGB=∠EBG. 所以∠HGB=∠HBG,可推知BF=HB=HG=AH+AG=EC+AG.
3. 第(3)问的解题分析
第(3)问是融合了几何运动与三角函数的综合题,涉及图形的平移和线段的旋转,求解本题的关键是确定B′的运动轨迹,而实际上点B′的运动轨迹与点E′的运动轨迹相关,即两者存在联动. 学生在解答时若不能把握动点之间的联动性,则很难确定关键点的轨迹,也就无法确定△ABB′周长的最值情形. 其中“瓜豆原理”是动点联动性分析的关键知识,教学中需要结合图形重点讲解.
突破该问的基本思路是提取动点B′的运动轨迹,构造旋转相似,结合“瓜豆原理”分析即可. 后续可将问题转化为“将军饮马”模型,结合对称知识确定△ABB′周长的最小值,此时就为点B′的位置,图形即可确定,构造直角三角形便可求得tan∠DAB′的值,具体过程如下.
结合平移知识可知,点E′的运动轨迹为过点E且平行于CF′的一条线段. 利用“瓜豆原理”分析点B′的运动轨迹. 过点E作EL⊥BE,使得EL=BE,构造等腰直角三角形△BEL,如图7所示. 易证图7中阴影部分的两个三角形为相似关系,故有∠B′LB=∠E′EB=45°,所以∠B′LE=90°,即点B′在过点L且平行于BE的射线上.
△ABB′的周长可表示为C=AB+BB′+AB′,其中AB为定值,则三角形周长的最小值由“BB′+AB′”来决定,符合“将军饮马”模型. 延长LB′,作点A关于LB′的对称点A′,由对称性可知AB′=A′B′,则BB′+AB′=BB′+A′B′. 分析可知,当点A′,B′,B三点共线时,BB′+A′B′可取得最小值,此时点B′为A′B与直线L的交點,如图8所示. 可证图8中有△ANB′∽△A′OB,由相似性质可得=,其中OB=1,AN=-1,A′O=2-1,则NB′=. 而tan∠DAB′=tan∠AB′N==2-1,即tan∠DAB′的值为2-1.
围绕教学深入思考
上述针对学生的思维能力展开考题探究,问题共有三问,后两问的难度较大,问题各自独立,又具有一定的知识联系,综合性极强. 笔者经过深入思考,提出了相应的建议.
1. 基础强化,知识联网
概念、定理、定义、公式是初中数学学习的重点,也是综合性问题构建的基础,深刻理解知识本质,掌握方法技巧,才能灵活破解问题. 本题中,平行四边形的性质、勾股定理、相似或全等三角形的性质是破题的知识基础,若学生不能充分理解知识内涵,不能灵活运用转化,就会导致解题失败. 教师要转变“重解题,轻基础”的观念,在教学中重视教材基础知识的讲解,并结合考题指导方法运用,从根本上提升学生的解题能力.
2. 重视审题,过程推理
本题中含有大量的信息条件,涉及平移、旋转两大几何运动以及周长最值、三角函数等熟悉的知识模块. 从题干信息入手,理解问题条件,掌握图形特点十分重要,这也是审题的重点内容. 部分学生在读题过程中不注重条件的挖掘,难以深刻理解图像所隐含的信息,解题时就容易出现思维障碍. 在日常教学时,教师要依托教材习题,指导学生掌握正确的审题方法,引导学生转化信息条件,进行过程体验,让学生在图形变换、过程分析中提升思维能力,培养理性分析的习惯.
3. 注重积累,总结模型
上述问题的综合性很强,尤其是最后一问融合了众多模型,如与联动相关的“瓜豆模型”、与线段最值相关的“将军饮马模型”,这些模型为后续的破题提供了条件. 虽然数学模型不是教材的重点内容,但总结模型、提取结论可有效提升解题效率. 因此,在实际教学中,教师不能一味地解题而忽视知识模型的总结,要引导学生关注图像模型,总结模型结论,进而形成相应的解题策略;同时,要注重多角度探究模型,拓展模型结论,引导学生在学习时举一反三,在探索与思考中获得知识与能力的提升.
3027501908227

