借问题情境展课数学堂活力
穆金勇

[摘 要] 数学教学中创设问题情境具有重要的教育意义,其不仅有利于学习兴趣的提升,而且能发挥学生的主体作用,培养学生动手能力和合作意识,促进学生思维发展,提升学生解决问题的能力. 因此,教师要在教学中恰当地、适时地创设问题情境,以此展现课堂活力、促进学生全面发展.
[关键词] 问题情境;学习兴趣;全面发展
贴近生活的、符合学生认知的问题情境的创设有利于引发学生思考,促进学习能力提升,然部分教师认为数学教学时间紧、任务重,问题情境的创设不仅消耗时间,而且课堂难以把控,其效率远远低于直接讲解,致使问题情境的应用不尽如人意,课堂沦为了教师“灌输知识”的主战场. 为了引起同行重视问题情境的创设,笔者就其在教学中的教育意义进行了剖析,以期共鉴.
有利于学生主体作用的发挥
学生是教学的主体,然在学习中学生常常感觉到数学内容枯燥乏味而无法激起学习的兴趣,因此其参与的积极性不高,其主体作用也难以发挥. 为了激发学生的好奇心,让学生成为课堂的主人,教师可以创设一些生动活泼的问题情境,如游戏、实验等,让学生带着强烈的求知欲参与教学实践,这样的课堂势必是高效的、生动的.
案例1 图形的位似.
师:请同学们拿出课前准备的橡皮筋. 你们可以用它绘制放大的三角形吗?(学生之前经历过图形放大和缩小的练习,很快画出了图形)
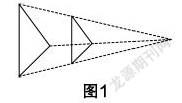
师:如图1所示,这是大家刚刚模拟放大的图形,它们相似吗?(教师用PPT展示图1)
生齐声答:相似!
师:观察图形的位置关系,它们有哪些特征呢?
生1:连接对应点并将连线延长后可以发现它们都过同一点.
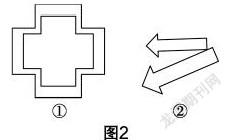
师:总结得很好!请各小组测量图2显示的两张图,测量后连接对应点,看看你有什么发现. (图2在课前已按小组发放)
生2:根据测量得到的数据可知,它们都是相似图形. 连接对应点后,如图3所示,可以发现图3①中的连线过同一点,但在图3②中找不到这样的点.
师:总结得很好,图1和图2①这样的图形就是我们今天要研究的主题——图形的位似. 它们有两个特点——(教师话音刚落,很多学生已经开始抢答了)
生3:首先是相似,其次对应点的连线过同一点.
师:很好!通过对图2②的观察,你们又有什么发现呢?
生4:图形的位似必须同时满足这两个条件,缺一不可.
在“图形的位似”的教学中,通过情境创设让学生先经历动手实验回顾图形的放大和缩小,进而感受相似;接下来鼓励学生在观察的基础上动手操作,从而发现“同一点”;最后引导学生总结和归纳“位似图形”概念. 在这一系列的数学活动中充分发挥了学生的主体作用,使抽象的概念教学变得生动、形象. 同时,在问题情境的渲染下,操作与思考相结合,课堂气氛活跃,激发了学生探究的积极性,让学生体会了数学学习的快乐.
有利于合作意识的提升
数学是一门实践操作较强的学科,然部分教师认为数学教学任务重、时间紧,没有时间“做”数学,因此这样动手操作所蕴含的丰富的知识内涵难以被发现. 同时,因为没有“做”的过程,学生很难发现问题,没有问题学生自然就问得少了,合作也少了,这样不利于学生合作意识的培养. 因此,在教学中要合理地创设情境,以问题为媒介,培养学生的动手能力和合作意识.
案例2 认识无理数.
师:课前让大家准备的小正方形纸片,大家都准备好了吗?
生齐声答:准备好了!
师:请大家拿出两张大小相同的小正方形纸片,剪一剪,拼一拼,看看能否拼出一个大的正方形. (学生立刻动了起来,很快有了答案)
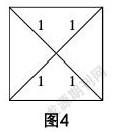
生5:将小正方形纸片沿对角线对折后剪开,然后将得到的4个等腰直角三角形纸片按照图4的方式进行拼贴.
师:很好!若小正方形的边长为1,大正方形的边长为a,你能求出a的值吗?
生6:根据勾股定理可知,a2=2.
师:a是整数吗?
生7:不是.
师:a是分数吗?
生8:也不是.
师:看来我们学过的数不够用了.
生9:用其他拼法是否可以求出a的值呢?(为了帮助学生更好地释疑,教师让学生通过剪拼寻找新的求值方法)
教师巡视后,将学生拼贴的结果进行了展示,学生采用了不同的方法进行求解,发现都不能求出a的精准值. 通过回顾有理数的概念,发现a不是有理数,于是a这一新数的出现激发了学生探究的热情,这为学生更好地认识无理数奠定了基礎.
教学中,教师让学生通过拼贴从感性上认识新数,在问题情境的引导下通过理性地分析感知新数存在的现实意义,进而凸显了无理数产生的必要性. 整个过程中,教师引导学生动手“做”数学,而且放手让学生自己“做”,不仅提高了学生的参与度,而且在“做”的过程中学生大胆尝试,积极合作,充分体验了探究的乐趣.
有利于提高解决问题的能力
在数学教学中,引入学生熟悉的生活情境,更容易让学生参与情境活动,进而在情境活动中通过观察、猜想、推理和分析,将情境活动中的感悟转化为新的技能,从而提升解决问题的能力.
案例3 相交线.
师:大家都会用剪刀,那你们知道为什么剪刀可以剪开物体吗?(学生只是会用,从来没有考虑过“为什么”,进而显得有些束手无策)
师:如果将剪刀转化为几何图形,你认为应该是什么图形呢?
生10:应该是两条相交线. (学生纷纷点头表示赞成)
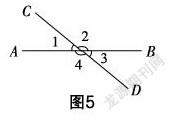
师:很好!如图5所示,当我们用剪刀剪物体时,图5上的角会如何变化呢?
生11:裁剪时,∠1和∠3会逐渐变小,∠2和∠4会逐渐变大.
师:你们发现∠1与∠3、∠2与∠4、∠1与∠2、∠3与∠4存在什么关系呢?
本课的教学重点之一是对顶角的概念及性质,为了淡化概念的抽象性,教师引入“剪刀剪物体”这一符合学生认知的生活实例,引导学生将实物转化为抽象的图形,通过对“剪刀剪物体”的观察和抽象引发学生对角的思考. 在这一过程中,生活情境的引入为学生提供了和谐的学习氛围,使得学生探究更加主动,课堂更加生动.
有利于促进思维发展
问题是引发思维活动的导火索,带着问题去思考才会使思维迸发耀眼的火花. 问题情境的创设是激发学生思维活动、提高学生思维水平、发展学生思维能力的重要手段之一,因此,为实现学生数学思维的发展,必须重视情境的创设.
案例4 探索三角形的全等条件.
师:请看PPT,小明家橱柜有两个同样大小的三角形挡板,然有一个出现了破损,小明的爸爸准备把破损的挡板换掉,这时他问小明:“现在我们请安装师傅为我们更换橱柜,我们需要提供哪些数据才能让安装师傅不上门就可以做一个同样大小的三角形挡板呢?”(教师用PPT展示图片)
生12:量出三角形挡板三边的长度就可以了.
师:你是怎么想的呢?
生12:因为我看到家里装修时师傅就是这样做的.
师:很好,看来你的生活经验很丰富啊,那么量三边的长度真的可以做出一样的挡板吗?还有没有其他办法呢?
本节课是一节很好的探究课,通过生活情境的引入让学生更加关注“全等”条件. 通过问题情境的创设,不仅直接引出了本节课的主题,而且激发了学生的好奇心和探究欲;学生的探究欲被激发后,教师引导学生从一个条件(一边、一角)到多个条件进行推理和验证,在推理和验证的过程中学生通过画一画、剪一剪、举反例等学习活动体验知识的形成过程. 在此过程中,学生充分体验了分类讨论在推理中的重要意义,进而提升了思維的严谨性. 另外,在探究中多角度观察和思考,对培养学生思维的广阔性和创新性也有着积极的意义. 通过师生和生生的合作交流,学生在理解和掌握知识的同时,提升了学生的思维水平,促进了学生的全面发展.
总之,数学教学中创设问题情境是激发学生学习兴趣的有力“武器”,其有利于学生思维发展,有利于学习能力提升. 因此,在教学中,教师要精心创设符合学生最近发展区的问题情境,以推动学生的全面提升.
3784501908288

