基于FDM技术的Hilbert曲线路径优化算法*

葛 啸 史廷春 黄志鹏 岳秀艳

(①杭州电子科技大学自动化学院，浙江 杭州 310018;②杭州电子科技大学图书馆，浙江 杭州310018)

3D打印技术又称增材制造(additive manufacturing, AM)技术，产生于20世纪80年代后期[1]，如今在医疗仪器、轨道交通及航空航天等战略新兴产业中都有重要的应用价值[2]，所以成型件的精度对其实际应用是至关重要的[3]。而成型过程中的翘曲变形是一个主要缺陷。在成型过程中由于填充路径而导致的材料冷却收缩时处于层间、层内的位置不同而导致翘曲变形[4]。而FDM技术是通过逐层累计喷射加热的热塑性材料来打印结构[5]，不恰当的路径设置会导致成品质量的降低[6]，所以成型时材料的填充路径对成型件的翘曲变形程度有着重要的影响。

目前存在着许多3D打印路径规划算法，平行线填充法、轮廓偏置填充法[7]和空间曲线填充法是最常用的3种方法[8]，许多路径规划方法是都是在它们的基础上优化而来的。平行线填充法填充路径相互平行，方法简单，使用最为广泛，但其打印时的方向为一固定方向，在很多时候会与成型件的表面有一定的夹角，打印时会出现台阶效应[9]。同时该填充方法在同一层面上的填充方向一致，会带来同方向的收缩应力，很大程度上会导致成型件产生较大的翘曲变形。Park S C等[10]针对填充角度与加工区域之间的关系进行了研究，提出了将路径分段存储最终连接而形成全局连续的路径。Yang J等[11]利用FASS曲线进行自适应路径填充。

轮廓偏置填充法可以很好地保持打印件边缘精度，是以其自身轮廓线为基础生成内部填充线的一种方式。这种方法可以有效地避免台阶效应，同时可以使材料冷却时的应力收缩没有一致性，减少翘曲变形的发生，有利于提高成型零件的表面精度质量，但其在形状复杂的轮廓填充时会存在断口[12]，也会在终点处产生多余的固化毛刺[13]。Held M等[14]提出利用一条Fermat螺线进行不间断填充。王腾飞[15]为了减少轮廓偏置时产生自相交进而提出一种等距偏置的路径规划算法；王益康[16]提出基于轮廓交点分组排序的混合填充方法，提高打印效率；翟晓雅等[17]将填充区域分为轮廓层，过渡层及内层，更适用于具有复杂边界及多连通区域的几何模型；张鸿平[18]等将轮廓偏置算法与并行栅格的方法进行了混合，提出了新的路径规划方法；韩兴国等[19]将蚁群算法运用到对多连通区域上不同环的打印次序上；为生成连续的空间扫描曲线，晁艳艳等[20]一方面保证成型件的表面质量，另一方面减少喷头的行程及启停次数，从而提出了基于网格法的分型中Hilbert曲线扫描填充算法，降低零件残余热应力，减小零件的翘曲变形量。

1 Hilbert曲线路径填充算法

对FDM式的3D打印中已有路径规划的描述，不难发现大多数传统路径填充方式都会存在填充路径不连续，喷头需不断启停的情况，降低了打印效率。在制件成型过程中，打印头必然会多次启停变速，无法保持恒定不间断的速度，在路径的拐角处降速并且存在打印头启停和变速问题，影响打印效率以及造成制件成型质量差[21]，打印路径中如果存在一个方向上长的直线打印则会产生较大的翘曲变形[22]，同时，不合适的打印路径会引起不必要的材料各向异性[23]，使成型件在沿打印路径方向上的抗拉强度远远大于其沿横向方向的抗拉强度[24]。而Hilbert曲线填充则是一种连续的填充路径，减少电机启停次数就可以降低打印件的各向异性，提高打印效率[25]。由于Hilbert曲线其自身有多次转向的特点，具有明显的连续性和各向同性[26]，使单层截面上的应力收缩方向是分散的且没有一致性，在较大截面上产生翘曲变形的可能性大大减小。但它存在的问题是曲线所有的转弯处都是直角，在此处打印时必定会造成打印喷头一个方向速度的突然变化，这样不仅会影响打印电机的使用寿命，降低打印效率，还会造成精度的降低[27]。

故本文提出一种优化的Hilbert曲线路径规划方法，在保持路径连续的基础上进一步优化打印过程中的速度，从而达到提高打印件的精度。基于Hilbert曲线优化的路径规划方法的具体实施步骤如下：

(1)确定层高，对打印件进行分层切片；首先对切片层轮廓进行轮廓偏置，使之可以更好地保持原有的外形轮廓而减少变形。

(2)根据轮廓偏置后的层面轮廓以及需要填充的实际需求，如填充率以及打印效率等生成相应阶数的Hilbert曲线。

(3)对生成的Hilbert曲线进行优化拟合，使用三次B样条曲线进行拟合，然后插值，使之生成光滑的曲线，将拟合后的曲线所有控制点坐标保存为txt文本文件。

(4)使用拟合后的曲线坐标生成G代码，导入打印机相应的打印软件中，实现打印。

2 填充路径生成方法

2.1 曲线拟合方式

曲线拟合的方式有很多，如B样条曲线拟合[28]、三次样条曲线拟合和贝塞尔曲线拟合等。三次参数样条曲线拟合属于样条插值曲线拟合，在拟合后曲线过所有样本点如图1，实线为原曲线，虚线为三次样条插值拟合后曲线，可以看出这样会产生额外不必要的行程，导致路径的增长，降低整体的打印效率。

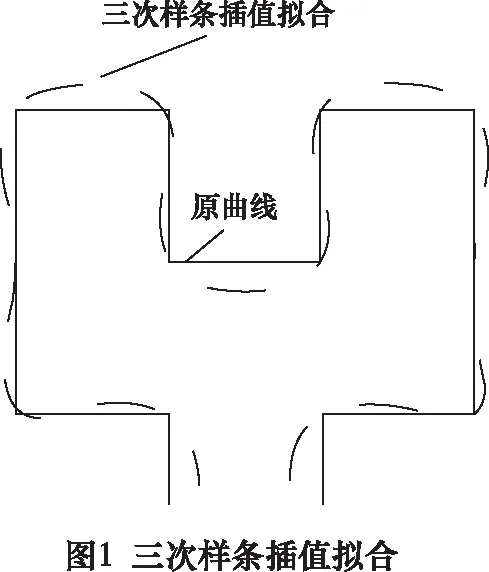
贝塞尔曲线只有第一个顶点和最后一个顶点落在控制多边形上，且曲线可以表示出控制多边形的导数、阶次和形状。但贝塞尔曲线拟合存在着不足之处：确定了控制多边形的顶点个数(n+1)，就确定的曲线的次数(n)；控制多边形的顶点越多，曲线的逼近程度越差。这两点使得贝塞尔曲线并不适用于Hilbert曲线的拟合。B样条曲线比贝塞尔曲线更贴近控制多边形，且曲线更加光滑，曲线的次数是根据需求确定的而不是由控制点的个数确定。在此，我们选择B样条曲线拟合。

常用的B样条曲线拟合有二次B样条曲线拟合及三次B样条曲线拟合，使用两种方法对Hilbert曲线拟合，对拟合后的曲线进行仿真打印分析，具体过程为：计算拟合后曲线相邻两点之间的距离，相加之后求得拟合曲线的总长度；然后，给定打印速度，求出打印相邻两点需要的时间，便可以判断出两种曲线填充的打印时间；使用打印相邻两点所用时间与这两点之间横向距离和纵向距离求出打印时x轴电机运行速度和y轴运行速度。便可以绘制出两轴打印速度时间图。打印过程中，x、y方向喷头移动速度如图2所示，可以看出，使用二次B样条拟合打印电机经过速度为0点的次数更多，且速度变化率更高，考虑打印效率及精度的综合因素，选择三次B样条曲线拟合作为曲线优化方法。

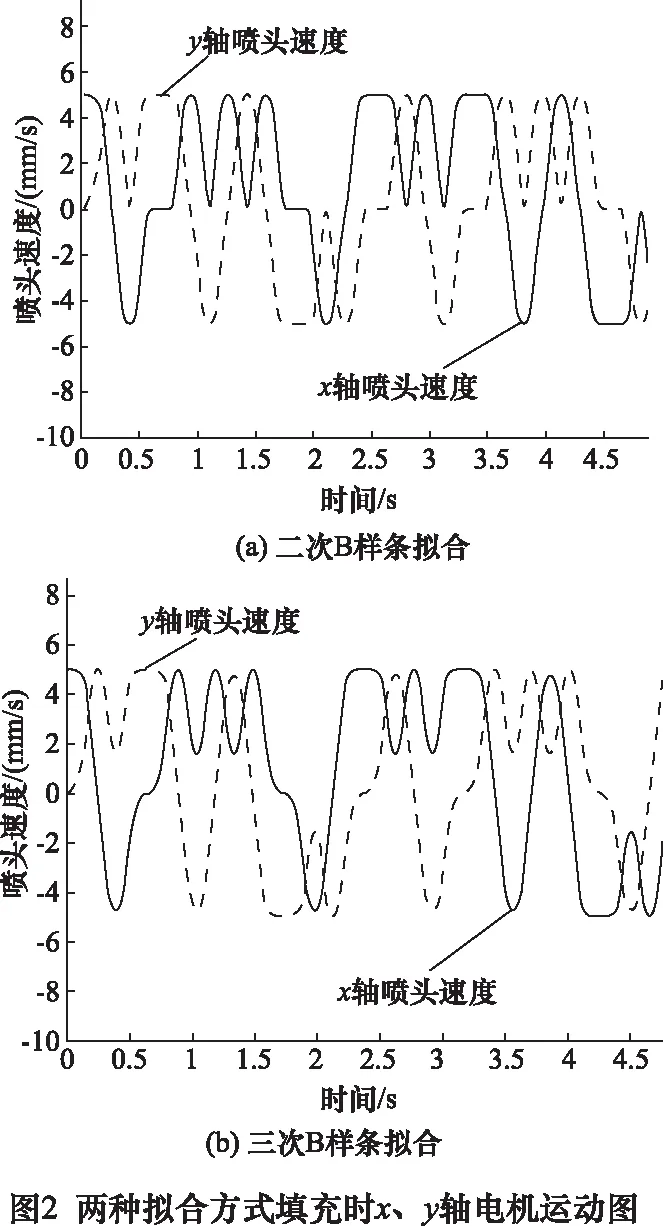
2.2 Hilbert曲线拟合

本文对Hilbert曲线拟合主要包括两个步骤:首先将曲线控制点的坐标输入，进行三次B样条平滑，把给定的点，平滑到B样条曲线上，不会增加点的数目；然后进行三次B样条拟合，在节点之间均匀插入指定个数的点，完成拟合。三次B样条曲线拟合方法中，n次B样条曲线的参数表达式为：

(1)

式中：Pi为给定的n+1个控制点Pi(i=0,1,0,...，n)的坐标;Fi,n(t)为n次B样条曲线的基函数，其形式为：

(2)

而三次B样条曲线的基函数为：

(3)

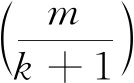
(4)

(5)

(6)

(7)

拟合后的Hilbert曲线如图3所示，实线为原Hilbert曲线，虚线为拟合后的曲线。可以看出，经过三次B样条拟合后的曲线在原曲线需要直角转弯处全都变得光滑，减少急转弯也就是减少打印过程中电机的快速变化，电机的变化率变慢可以使整个打印过程中残余应力变少，打印精度提高。同时，曲线的整体长度变得更短，这样会使打印时间减少，效率提高。

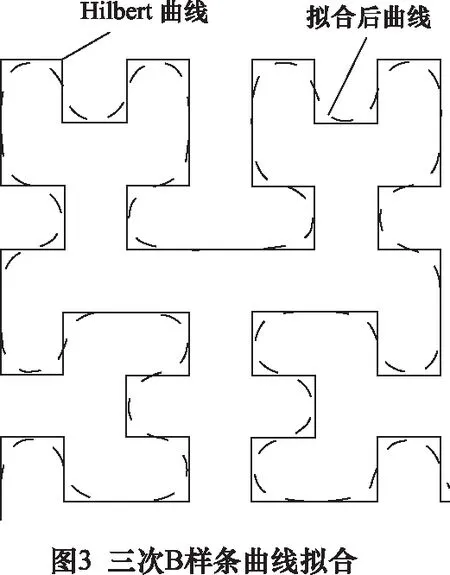
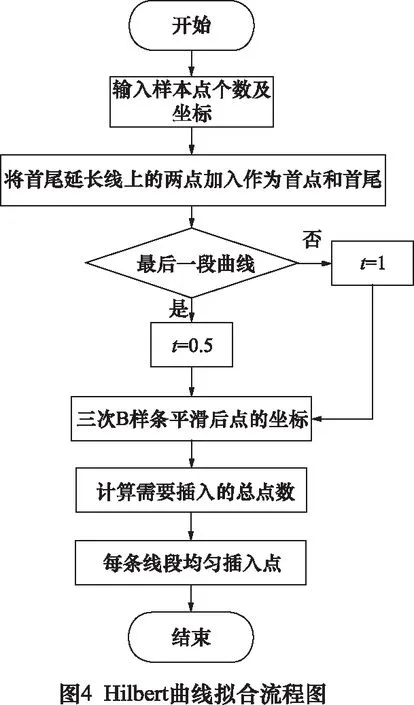
其算法流程图如图4所示，将输入的Hilbert曲线控制点的个数及坐标，将其按三次B样条曲线基函数整体平滑，对于首点和尾点，它们没有前一点或后一点，故需要将曲线前两点的连线延长，在延长线上取一点为第一个点。同理，在曲线最后两点的连线延长线上取一点为最后一个点，这样便可以将整条曲线的控制点平滑到新的曲线上。平滑后，点的个数不变。然后，在平滑后的曲线上进行插值拟合，每条线段上的插值个数可以根据实际需求指定，在每条线段中均匀插值，完成Hilbert曲线拟合的过程。

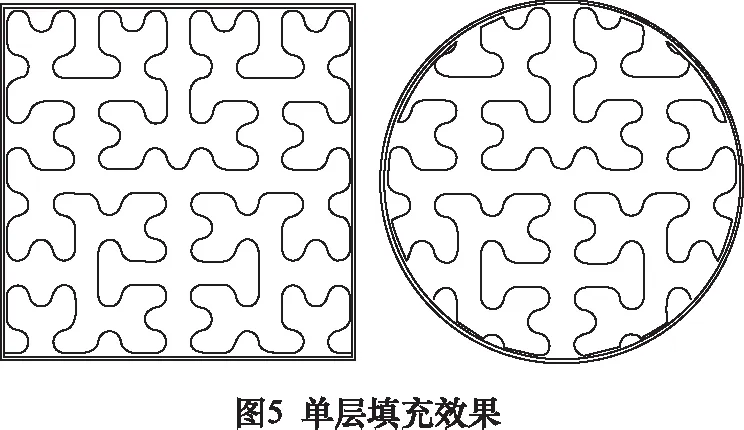
3D打印时，为保证打印件边缘较高的打印精度，通常会首先对打印件的切片层轮廓进行轮廓偏置，轮廓偏置次数一般设置为2～3次，本文取偏置次数为2；将偏置后的内轮廓使用拟合后的Hilbert曲线填充，图5为不同形状轮廓单层填充的示意图。

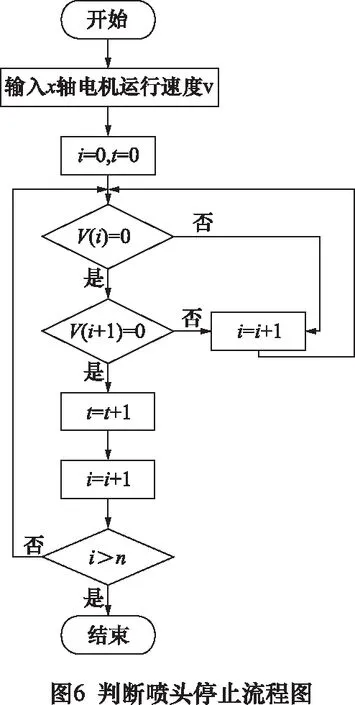
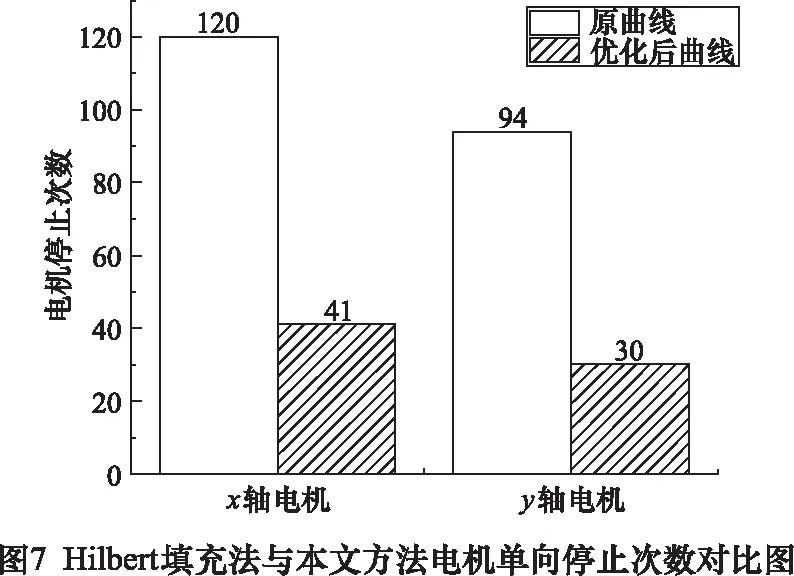
此外，优化后的曲线填充会使打印过程中喷头的停止次数大大减少。具体过程如图6，将连续2次停止的点记做电机的一次停止。图7所示为两种打印路径工作下，x轴电机停止次数减少了65.83%，y轴电机停止次数减少了68.09%。

3 实验结果及分析

3.1 3D打印机与基本参数

本实验使用型号为Prusa i3型打印机，材料为PLA，本文路径填充方法使用C++拟合，使用MATLAB保存为G-code来实现。G-code是最为广泛使用的数控编程语言，它可实现打印机喷头及热床的加热，通过坐标点控制喷头的移动[29]。Repetier-Host是一款切片软件，将STL文件导入其中后便可以使用Cura Engine对其进行分层和路径规划，生成G-code供机器打印。使用拟合曲线和原曲线的坐标点生成G-code，将其直接导入Repetier-Host，可以生成打印预览。

基本设置为喷头直径0.3 mm，打印速度为30 mm/s，空行程速度为70 mm/s，层高为0.2 mm，热床温度为60 ℃，喷头温度为200 ℃。

本文选取的打印样件是高为5 mm，边长为46.8 mm的长方体，以四阶Hilbert曲线进行填充，使用未优化过的Hilbert曲线和拟合后的曲线对其打印为1组，共打印10组样件，分析不同填充方法的打印时间、消耗材料以及翘曲变形的情况。

3.2 实验结果

打印结果可直接反映出打印填充方法优劣性，同样的样件打印时间及耗材对能否实现快速大批量生产有着重要的影响；电机的启停次数不光影响打印效率，频繁的停止会产生应力集中，发生翘曲变形。

由表1可以看出，对于相同的样件，优化前打印花费时间为1 805 s，需要材料4 062 mm，优化后则打印花费时间为1 734 s，效率提高了3.93%，需要材料3 877 mm，减少了4.55%。

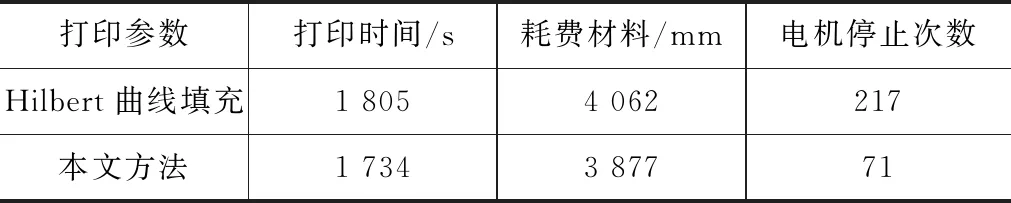
表1 打印结果对比

3.3 翘曲变形

翘曲变形影响打印件的成型精度，不仅会影响模型的美观性，甚至会使成型件丧失原有的使用价值。

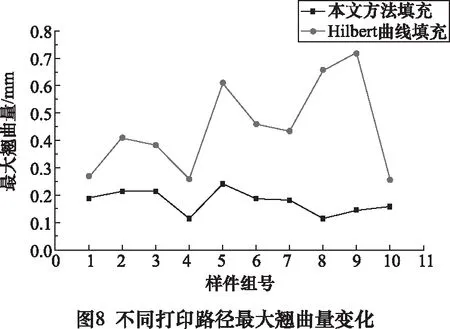
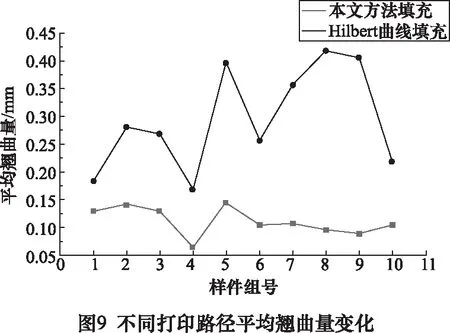
本文测量成型样件底层中心与四周边角处高度的差值来计算样件翘曲变形的情况，中心高度采用多次测量求平均值的方法计算。打印10组样件，分别测它们翘曲变形的情况，图8与图9分别为两种打印路径下，最大翘曲量变化和平均翘曲量变化曲线图。

使用Hilbert曲线填充样件的平均最大翘曲量为0.446 mm，总平均翘曲量为0.295 mm；使用优化后方法填充样件的平均最大翘曲量为0.175 mm，总平均翘曲量为0.112 mm，平均最大翘曲量减少60.7%，总平均翘曲量减少62.26%。

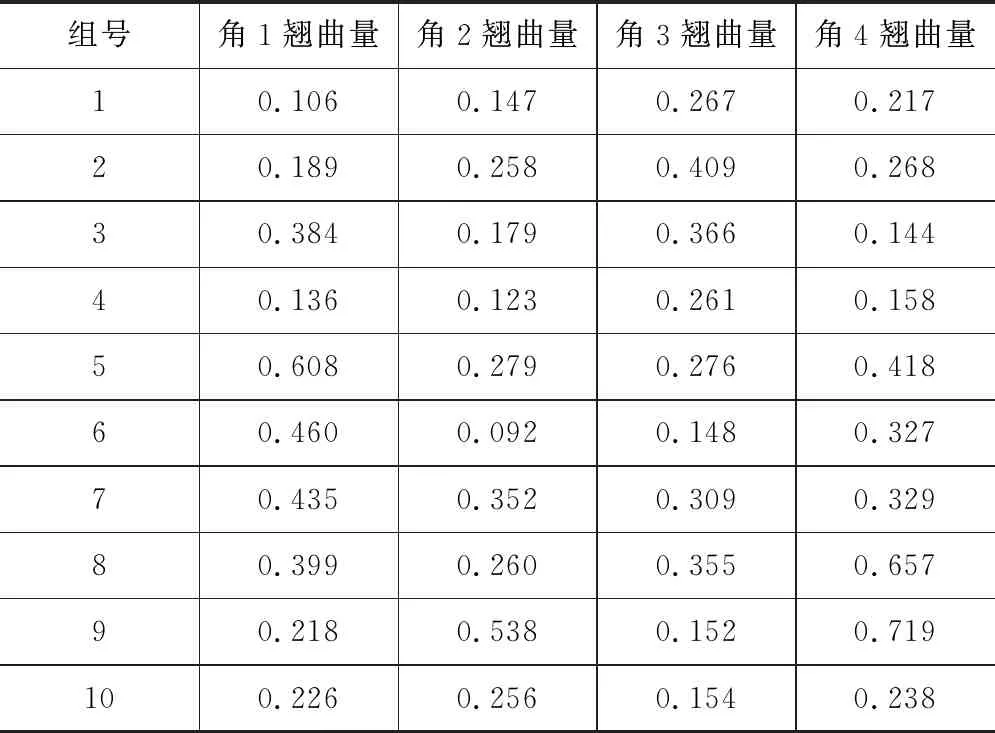
表2 Hilbert曲线填充翘曲量 mm

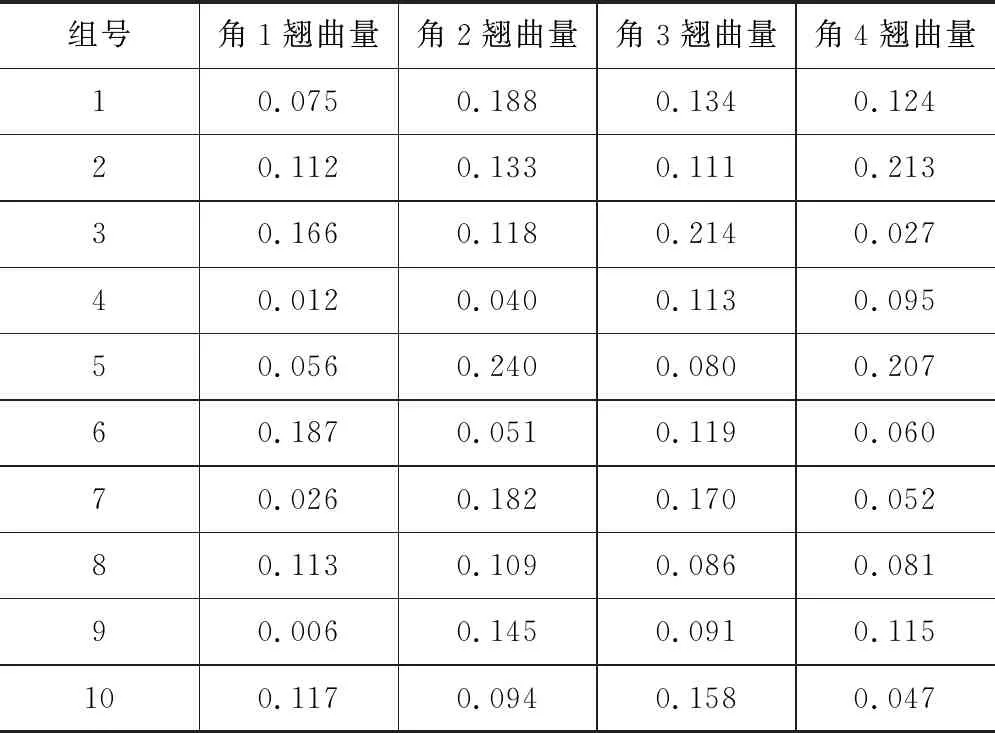
表3 本文方法填充翘曲量 mm

打印效果实物图如图10所示，以第7组样件为例，可以看出使用轮廓偏置和Hilbert曲线作为填充路径打印出的成型件在边角处存在轻微的翘曲变形，最大翘曲量为0.435 mm，平均翘曲量为0.356 mm，是由于打印时电机运转过快以及频繁换向导致打印时散热不均匀产生残余应力，翘曲变形集中体现在成型件最下层的边角处；使用轮廓偏置和优化后曲线作为打印填充路径时，最大翘曲量为0.182 mm，平均翘曲量为0.107 mm。

4 结语

3D打印中成型件的精度至关重要，本文从填充路径的连续性、填充时喷头运行的流畅性方面入手，在连续的Hilbert曲线的基础上，优化了曲线的形状，使喷头在填充时减少在单方向的停止次数，速度变化更为平缓，进而减少成型件的翘曲变形。此外，本文从打印时间、耗费材料、电机停止次数及翘曲变形等方面进行实验验证，对比了本文方法与使用Hilbert去曲线填充的差别。

实验证明，基于Hilbert曲线优化填充曲线和轮廓偏置相结合，不仅具备了轮廓偏置算法的较高外轮廓精度的优点，同时经过三次B样条拟合后的Hilbert曲线填充降低了打印过程中电机变化率，减少了电机转向次数，进而减少打印件的翘曲变形，提高打印件精度。G-code的生成使算法可以在大多数FDM打印机直接实现打印。

此外，尽管该方法在填充路径连续及喷头速率变化减缓等方面有一定的优点，可以减少翘曲变形，提高打印效率，但轮廓偏置固有的对于复杂边界偏置时容易产生偏置线自相交问题依旧存在。此外，本方法会存在轻微的翘曲变形以及难以填充多连通区域复杂模型的问题。今后的工作将针对本方法在用于多连通区域复杂模型的填充时会出现路径不连续，曲线难以完整填充等问题的优化，进一步优化填充曲线。