)的局部支集样条函数的构造方法
路 游,张丽娜,汪春晓
(中国石油大学(北京),北京 102249)
路 游,张丽娜,汪春晓
(中国石油大学(北京),北京 102249)
在计算几何领域中,对于拟合、插值、重构,Box样条函数已显示出其重要的应用优势,是一类应用广泛的插值函数。但是在拟合算法中,大量的工作量是计算Box样条基函数,因此,减少Box样条函数的计算量,可以提高Box样条的拟合速度。研究目的在于构造出具体的Box样条函数的分段多项式形式,提高拟合算法的计算效率。首先,应用积分方法以及Box样条的对称性和轮换性分析Box的显示表达式。然后,通过对七方向Box样条在三维空间中进行Ⅲ-型剖分,在剖分上构造出三维空间中分段多项式形式的Box样条的支撑函数,并且给出了具体的推导过程。最后实现了分段多项式形式的Box样条函数。另外,由此支撑函数构造了拟插值算子和重构算法。通过此算法的数值实验,在拟合算法效率上得到了预期的结果。
支撑函数;剖分;积分;胞腔;分段多项式
0 引 言
样条函数是一种特殊的具有一定光滑性的分段函数,在计算机几何与飞机、船舶制造等领域均有重要应用。1946年,数学家I.J.Schoenberg系统地建立了一元样条函数的理论基础[1]。从60年代开始,样条函数得到了迅速的发展和应用。1966年,H.B.Curry和I.J.Schoenberg提出了一元B样条函数,一种定义B样条函数的几何直观方法[2]。1975年,以王仁宏为代表,采用函数论与代数几何的方法,建立了任意剖分下的多元样条函数的理论框架,并提出了光滑余因子协调法。1976年,de Boor将对一元B样条的几何解释推广到多元样条。目前研究多元样条的方法大致上分为三类。
(1)光滑余因子协调法,以王仁宏[3]为代表,在文献[4]中也提出了三维非均匀空间中多元样条函数构造方法。
(2)B-网方法,以Farin[5]为代表。
(3)B-样条方法,亦称投影子法,以Schoenberg[2]、de Boor[6]和Micchelli[7]等为代表。
近年来,对样条函数进行了广泛研究。文献[8-10]介绍了多元样条的应用研究,B样条在模糊系统中的应用,将Box样条应用到等值面可视化方法等。文献[11-15]研究了B样条的图像插值方法、B样条的数值流形和时间积分方法,同时研究了Box样条与控制网之间的关系,得出了Box样条与光滑拼接的Bezier曲面的充分条件,讨论了Box样条的体数据建模分析。另外,从向量的角度构造出三元Box样条[16]和在随机层面构造出特殊的随机Box样条[17],但都未给出Box样条函数的具体表达式。
将一元样条向多元样条扩展的方法:张量积,将一元基函数通过张量积(乘积)得到多元样条的基。但是,张量积形式的扩展方法存在一些缺点:首先,由一元B样条基的张量积构造的基函数,使其参数域只能在矩形的区域上,而对于非规则的参数域,只能由经过剪裁和拼接的矩形域上的NURBS曲面得到。其次,张量积形式生成的基函数,使得生成的曲面次数升高,次数较高的曲面使运算变得复杂,甚至影响拟合曲面的几何性质。而Box样条作为非张量积函数,提供了一个完美的数学框架,其能构造一类具有可变的形状和可变的局部的支集,它是进行各种重建或重构工作的有力工具。同时,在多元样条函数的理论和应用中,Box样条在对于给定剖分和指定的光滑度上,具有次数较低的分片多项式。
文中在总结样条函数现有成果的基础上,选择广泛采用的积分方法作为研究对象,主要利用Box样条函数的显示表达式和三维空间的Ⅲ-型剖分,通过积分方法构造样条函数的计算机实现过程及机制。
1 Box样条函数的积分方法
在三维空间R3中,设Δ为区域截断菱形十二面体D⊂R3上的一个剖分区域,且Δ将区域D分为有限个胞腔。函数集合Cμ(μ=2)样条函数,如果在每个胞腔中,多项式p的次数均不超过四次,即p∈Pk,则有:

三元样条在局部支集外取零值。如果它的支集最小,则一个非平凡的局部支集三元样条即为一个Box样条。
Bijk(x,y,z)=B(mx-i,ny-j,qz-k),i=0,1,…,n+1,j=0,1,…,m+1,k=0,1,…,q+1
1.1 三维Box样条
在文献[14]中,可以将二维空间的ZP元素推广到三维空间的Box样条。其中,二维样条函数是由正方形及其四个方向的对角线形成,三维样条函数是由立方体的三条边和四条对角线所得。三维中七方向Box样条表示为:

在三维七方向的Box样条中,三坐标方向构成的Box样条支集是一个立方体;四对角线方向构成的Box样条支集是一个菱形十二面体(见图1);七方向构成的Box样条支集是一个被截断的菱形十二面体(见图2),其由立方体和菱形十二面体上指示函数的卷积生成,具体表达式为:
M(E1,E2)(x)=(ME1*ME2)(x)
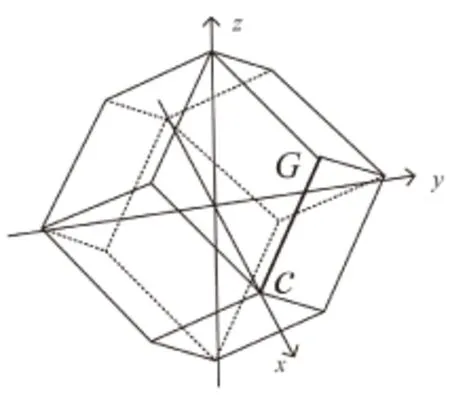
图1 MΞ2的支集菱形十二面体

图2 M的支集截断菱形十二面体
1.2 B样条的非组合积分构造方法


1.2.1 二元函数沿一个方向积分

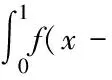
经过上面的转换,很容易用定积分的知识得出积分结果。对于图3中的点P(X,Y),与非零区域交于A,B两点,则有:



图3 特征函数及ZP元素
1.2.2 二元函数沿两个方向积分
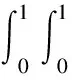

图4 特征函数及ZP元素
这样有:
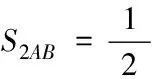
A(X,Y)=P(X,Y)+t1×(1,-1)
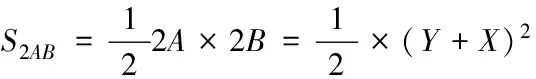
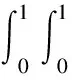
1.2.3 三元Box样条函数积分
对于Box样条的基函数[19]可由式(1)求出:
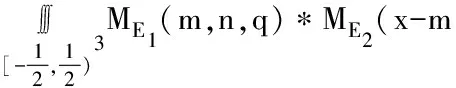
(1)
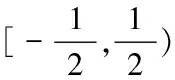
变量点(x,y,z)的取值范围即为三维Box样条的局部支集。同时,考虑ME2的表达式[7]:
ME2(x,y,z)=2max(0,1-max(|x|+|y|,|x|+|z|,|y|+|z|))
根据x,y,z在三维坐标中的对称性,可将x,y,z映射到第一象限,则其在第一象限上可表示为:
ME2(x,y,z)=

同样地,根据x,y,z的轮换性,可将第一象限划分成6部分(即为x≥y≥z≥0,y>x≥z≥0,y≥z>x≥0,z>y≥x≥0,z≥x>y≥0,x>z>y≥0),式(1)在区域x≥y≥z≥0上进一步表示为:
ME2(x,y,z)=2(1-x-y),x+y≤1,x≥y≥z≥0
(2)
那么,可在x≥y≥z≥0上对截断十二面体进行Ⅲ-型剖分,剖分结果如图5所示。则Box样条函数的支撑域,截断菱形十二面体即为菱形十二面体的指示函数ME2(x,y,z)与立方体[x-1/2,x+1/2)[y-1/2,y+1/2)[z-1/2,z+1/2)的指示函数常数1的卷积。
其中,限定x,y,z的范围在一个剖分上(如图5中13个剖分),各剖分为:
0≤z≤y≤x≤1/2
y≥z≥0,x≥1/2,x+y<1
z≥0,y≤1/2,x+z≤1,x+y≥1
x≥y>1/2,z≥0,x+z≤1
x≤1,z≤y≤1/2,x+z>1
x≤1,y>1/2,x+z>1,y+z≤1
x>1,y≥z,x+y≤2,y+z>1
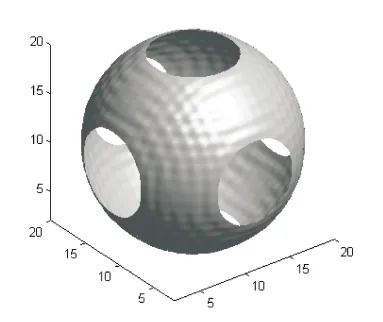
y>1/2,1 z≤y≤x≤1,y+z>1 y>1/2,0≤z≤x-1,x+y≤2 z≤y≤1/2,1 0≤z 0≤z≤y 图5 剖分结果 可设Q为三维空间区域R3中以原点为中心,以(1,0,0),(0,1,0),(0,0,1),(-1,0,0),(0,-1,0)和(0,0,-1)为顶点的菱形十二面体。在三维非均匀的剖分上,连接正对的三个对角面可以得到一个四面体剖分x≥y≥z≥0。在此基础上,该四面体继续进行剖分,可得到如图5的剖分结果,形成13个胞腔。 P1(x,y,z)=1/12 (9-24x2+16x3-24y2+24xy2+8y3-8xy3+4y4-24(-1+x) (-1+y)z2+4z4) P2(x,y,z)=1/24(17-48y2-48z2+8(x-9x2+8x3-2x4+6xy2+2y3-2xy3+y4+6(x+y-xy)z2+z4)) P3(x,y,z)=1/24(25+56x3-16x4-24x2(2+y)-48z2-8x(2-6y-3y2+2y3+6(-1+y)z2)+8(y(1+y)(-3+y2)+6yz2+z4)) P4(x,y,z)=1/3(3+7x3-2x4-3x2(2+y)-y(2+(-3+y)(-2+y)y)-6z2+6yz2+z4+x(-2+6z2+y(6+(3-2y)y-6z2))) P5(x,y,z)=1/24(37-12x4-24y2+8y3+8y4+24x2(y(-2+z)-2z)+8x3(4+y+z)+4z(-8-6z+z3)-8x(7+(-3+y)y(3+2y)-9z+6yz+3y(3+2y)-9(-1+y)z2+z3)+8y(-4+z(3+z(3+z)))) P6(x,y,z)=1/6(9-3x4-2y(3+(-3+y)(-2+y)y)+6x2(y(-2+z)-2z)-8z+6yz+6(-1+y)z2+2yz3+z4+2x3(4+y+z)-2x(7+(-3+y)z+6yz+3(-1+y)z2+z3)) P7(x,y,z)=1/6(12-16x+8x3-3x4-16y+24xy-12x2y+2x3y+4y3-2xy3-y4+2(-2+x+y)3z) P8(x,y,z)=1/6(-2+x+y)3(-2+x-y+2z) P9(x,y,z)=1/6(13+x4-2y(3+(-3+y)(-2+y)y)+6x2(-2+y)(-2+z)-8z+6yz+6(-1+y)z2+2yz3+z4+2x3(-4+y+z)-2x(15+(-3+y)y(3+2y)-9z+6yz+3(-1+y)z2+z3)) P10(x,y,z)=1/3(-1+x-y)(-2+x+y)3 P11(x,y,z)=1/24(53-32y-32z+4(x4+2y2(-3+y+y2)+6x2(-2+y)(-2+z)+6yz+6(-1+y)z2+2yz3+z4+2x3(-4+y+z)-2x(15+(-3+y)y(3+2y)-9z+6yz+3(-1+y)z2+z3))) P12(x,y,z)=1/24(65+8x4-72x2(-2+y)+8x3(-7+2y)-8x(-2+y)2(5+2y)+8y(-5+y(-3+y+y2)) P13(x,y,z)=1/24(3-2x)4 其他多项式可由上述多项式按对称原则和轮换原则得到。 设局部支集函数B(x,y,z)是定义在R3上的函数,在区域Q之外取零值,其在每个胞腔上的表达式为pi(x,y,z)。那么,Box样条的局部支集函数在三维空间中具有二阶连续偏导数,即:B(x,y,z)∈C2(R3),且在Q内恒正。因此,B(x,y,z)是关于图5剖分的三元Box样条。 (1)数据准备。 对三维空间中散乱数据点可组成一个三维矩阵A,作为输入数据点。 从上面的推导过程可得出非组合积分方法,构造分段多项式形式的Box样条支撑函数算法如下: ①按照图5所示对四面体进行编号,共有13个非零区域,编号从1~13。编号原则是按照四面体中的点引出的积分向量构成的区域,与初始非零正方形区域交点的位置一致性来划分。 ②对四面体区域Δi计算从区域中的点引出的两个向量构成的区域与非零正方形的交点,进而求出公共面积上的表达式。 ③四面体区域Δi编号加1,如果小于13且大于2则继续,否则完成退出。 将上面积分方法构造出的局部支集函数,运用到多面体的构造中去。对于给定的输入数据点,映射到区域x≥y≥z≥0上,根据对称后所在的胞腔,代入Box样条分段多项式,求解输入点的样条基函数。为简便,将Δmnq在区域Q上的剖分仍记作Δmnq,设: Bijk(x,y,z)=B(mx-i,ny-j,qz-k) (3)构造拟插值算子。 三维空间中的三变量非张量积Box样条可表示为: 其中,拟插值算子[4]为: (4)绘制等值面。 (5)分析拟合算法中,求解输入数据点样条基函数的时间复杂度。 以散乱数据点组成的41*41*41三维矩阵A,作为输入数据点,对拟合出的80*80*80三维矩阵A,在处理器PIV-2.10GHz,内存为4.0GB的普通个人电脑上绘制任意形状的等值面,结果如图6所示。 通过上述算法的程序实现分析,已知n个数据点,设p为三维空间中一个点映射到区域x≥y≥z≥0上的时间,q为一个点代入多项式求值的时间,则求解数据点样条基函数的时间可表示为: f(n)=n*p*q (3) 图6 曲面x2+y2+z2-1等值面 对式(3)分析可知,其时间复杂度与数据点的个数以n增长,所以该算法求解数据点的Box样条函数基函数的时间复杂度为Θ(n)。 与一般乘积形的B样条相比,首先,在每一块胞腔上的多项式次数是四次,且在边界上具有二阶光滑度。而乘积形样条,三个一元二次B样条相乘,不具有光滑度;三个一元二次B样条相乘,其在剖分上的多项式次数是六次,而文中构造出的Box样条在相同的光滑度的情况下,每块胞腔上的次数较多,增加了运算量。其次,文中的Box样条拟合的图形真实感与乘积形B样条绘制的相同。 文中通过应用积分方法构造了Ⅲ-型剖分上的Box样条的支撑函数,并利用Box样条的对称性和轮换性,推导出三维空间中的Box样条支撑函数显式表达式,且给出了具体的推导过程。 在拟合算法中,大量的工作量是计算Bijk(x,y,z)。如果对每个数据点直接进行卷积计算,显然此方法存在一些不足。首先,数值积分的计算都有误差;其次,由于需要对输入的每个数据点进行数值积分,在运算效率上比较低。而文中算法采用Box样条支撑函数解析表达式进行计算。在效率上,避免了大量的重复积分,大大提高了Box样条的拟合速度。 [1]SchoenbergIJ.Contributionstotheproblemofapproximation ofequidistantdatabyanalyticfunctions[J].QuarterlyAppliedMathematics,1946,4:45-99;112-141. [2]CurryHB,SchoenbergIJ.OnPolyafrequencyfunctionsIV:thefundamentalsplinefunctionsandtheirlimits[J].JAnalyseMath,1996,17(1):71-107. [3] 王仁宏.多元齿的结构与插值[J].数学学报,1975,18(2):91-106. [5]FarinG.BezierpolynomialsovertrianglesandtheconstructionofpiecewiseC’polynomials[D].Brunel:Univ.ofUxbridge,Middlesex,1980. [6]deBoorC.SplineaslinearcombinationofB-splines[M]//LorenzGG,ChuiCK,ShumakerLL.ApproximationTheoryII.NewYork:AcademicPress,1976:1-47. [7]DahmenW,MicchelliCA.Recentprogressinmultivariatesplines[M]//ApproximationtheoryIV.NewYork:AcademicPress,1983:27-121. [8] 郭庆杰.多元样条若干理论与应用研究[D].大连:大连理工大学,2015. [9] 谭彦华,李洪兴,马秀娟,等.B样条函数在模糊系统中的应用[J].控制理论与应用,2013,30(11):1445-1456. [10] 刘 晓,方美娥,张 楠.基于7方向Box样条的等值面可视化[J].杭州电子科技大学学报,2015,35(5):63-67. [11] 魏晓静.基于B样条函数的图像插值方法研究[D].大庆:东北石油大学,2014. [12] 温伟斌.基于B样条插值的数值流形方法与时间积分方法的研究[D].重庆:重庆大学,2014. [13]ZengXiaoming,ZhouGuorong,YangLianqiang.Bestboundsonthedistancebetween3-directionquarticboxsplinesurfaceanditscontrolnet[J].AppliedMathematics:AJournalofChineseUniversities,2013,28(2):147-157. [14] 杨联强,王 东.三元四次箱样条曲面与Bezier曲面的光滑拼接[J].计算机工程与应用,2013,49(23):119-121. [15]FangMeie,LuJia,PengQunsheng.Volumetricdatamodelingandanalysisbasedonseven-directionalboxspline[J].ScienceChinaInformationScience,2014,57(6):1-14. [16] 李 玲,路 游.三元Box样条构造方法的实现[J].计算机技术与发展,2009,19(11):45-48. [17] 于 巍.一类随机Box-样条的逼近问题[J].甘肃联合大学学报:自然科学版,2010,24(5):14-15. [18]deBoorC.Boxsplines[M].NewYork:Springer-VerlagInc.,1993. [19]EntezariA,MollerT.ExtensionsoftheZwart-PowellboxsplineforvolumetricdatareconstructionontheCartesianlattice[J].IEEETransactionsonVisualizationandComputerGraphics,2006,12(5):1337-1344. LU You,ZHANG Li-na,WANG Chun-xiao (China University of Petroleum-Beijing,Beijing 102249,China) In the field of computation geometry,for fitting,approximation,reconstruction,Box spline has showed its important application advantages and it is a kind of widely used interpolation function.But in the fitting algorithm,a large amount of workload is to calculate the Box spline.Therefore,the method of improving the fitting speed of Box spline is to reduce the calculation of it.The purpose of the research is to construct the polynomial form of the Box spline function,and improve the efficiency of the algorithm.By 3-partition in the three-dimensional space,the integration method and the symmetry and rotation of Box spline are used firstly to analyze its explicit form.And then the Box spline in polynomial form is constructed in the type-3 partition.Finally,the piecewise polynomial form of Box spline function is realized.Besides,the specific procedure is given.In addition,by using the support function,quasi-interpolation operators and reconstruction algorithm are constructed.Through the numerical experiments,the expected results are obtained in the efficiency of fitting algorithm. support function;partition;integration;cell;piecewise polynomial 2016-03-01 2016-06-09 时间:2016-11-22 国家自然科学基金资助项目(60873093) 路 游(1957-),男,博士,副教授,研究方向为计算几何、图形学、虚拟现实;张丽娜(1989-),女,硕士研究生,研究方向为计算机可视化。 http://www.cnki.net/kcms/detail/61.1450.TP.20161122.1227.012.html TP391.7 A 1673-629X(2017)02-0110-06 10.3969/j.issn.1673-629X.2017.02.025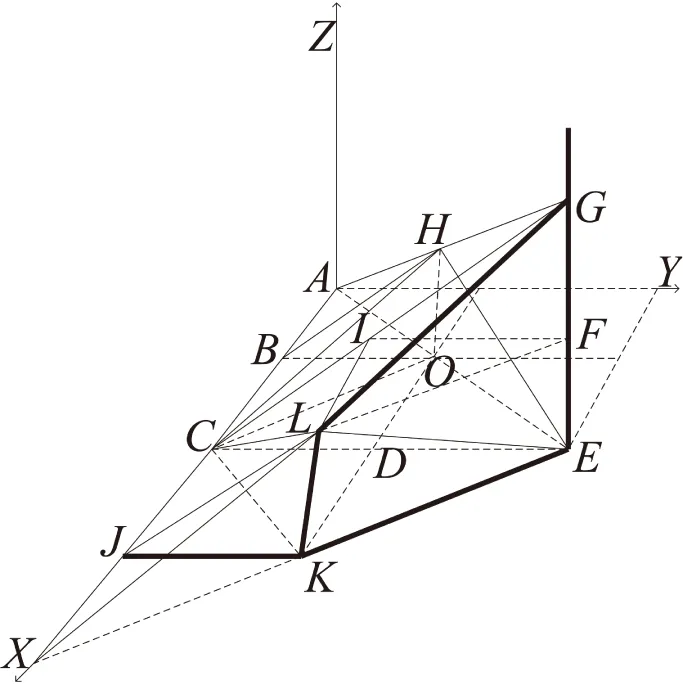
2 三元Box样条的局部支集函数
3 空间体的拟插值算法

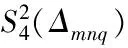

4 实验结果
5 结束语


