基于数值积分的最佳平方逼近样条函数
钱 江, 刘雯星
(河海大学 理学院,江苏 南京 211100)

为了得到更为直观的基函数表达式,本文拟构造一组样条正交基,并将其与数值积分结合,应用于最佳平方逼近问题。
1 有限闭区间上的一元三次B样条基函数
B样条有不同的定义方式,常见的有de Boor递推算法、差分定义和光滑余因子方法。采用de Boor递推算法确定三次B样条函数,需要多次递推计算样条基函数,计算量大。而利用光滑余因子协调法,不论是重节点还是均匀节点,只需求解线性方程组即可。
为了更好地将样条应用于最佳平方逼近,本文考虑使用由光滑余因子方法得到的B样条函数。
引理1.1设{x0,x1,…,xn}是步长为h的均匀节点,则在区间Ii=[xi,xi+1],i=0,1,…,n-1上存在唯一一组一元三次B样条基函数

(1)
由光滑余因子协调法[1]可直接计算得到(1)式。
上述定理给出了在均匀节点上的三次B样条基函数,下面给出区间端点处带重节点的B样条基函数。
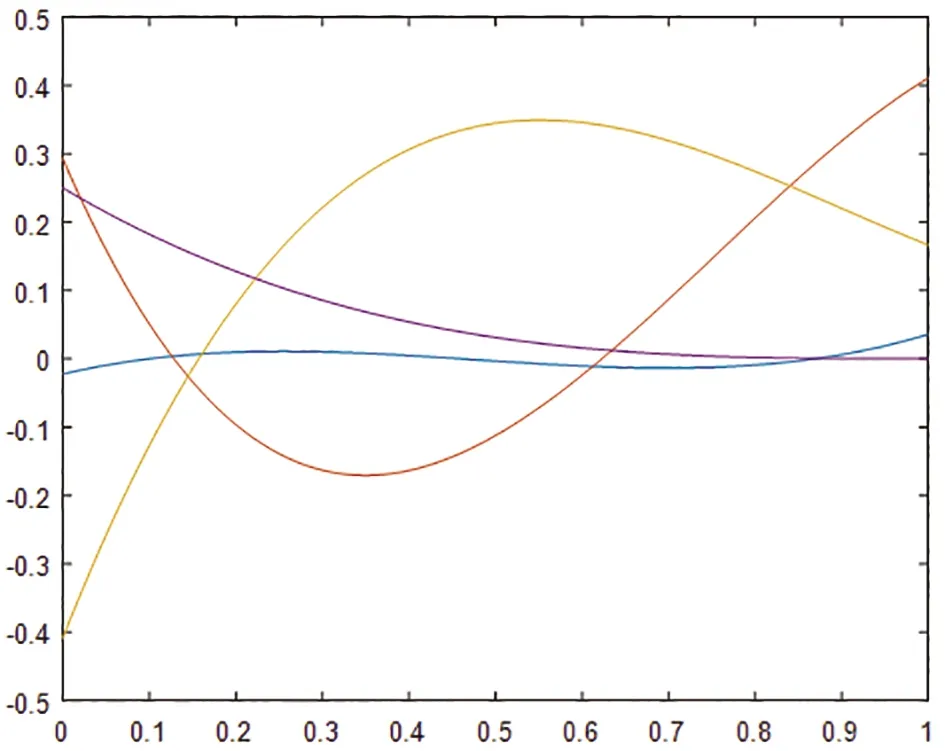
引理1.2设节点为x-3=x-2=x-1=x0 (4) 其中,对于左端点带有二重节点、三重节点、四重节点的情况, 其协调方程分别设为 类似地,区间右端点带重节点的三次B样条基函数表达式如下。 引理1.3设节点为xn-6 (5) (6) (7) (8) 有了上述公式,任意一元三次B样条基函数的内积运算便快捷了许多。 p(x)=c0s0(x)+c1s1(x)+c2s2(x)+c3s3(x), 则 (9) 化简后得 (10) 由引理1.4即可简便算出(sm,sn),m,n=0,1,2,3。 设{x0,x1,…,xn}是步长为h的均匀节点,对区间[xi,xi+1],i=0,1,…,n-1上的基函数s0(x),s1(x),s2(x),s3(x)作Schmidt正交化,得到P3上一组正交基β0,β1,β2,β3。 (11) 由于 所以有 (12) 这里 (13) (14) (15) 此时 (16) (17) (18) 此时 图1 [0,1]上基函数β0,β1,β2,β3的图像 图3 [0,1]上基函数的图像 图4 [0,1]上基函数的图像 图5 [0,1]上基函数的图像Fig.5 Graph of the basis function on [0,1] 定理3.1设{x0,x1,…,xn}是一组均匀节点,步长为h,β0,β1,β2,β3是P3中一组正交基,则∀f(x)∈C[xi,xi+1],i=0,…,n-1,存在f(x)基于梯形公式的最佳平方逼近函数 其中 (19) 证明:对(βk,f),k=0,1,2,3使用梯形公式,于是 从而得到f(x)基于梯形公式的最佳平方逼近函数。证毕。 定理3.1给出了均匀剖分下基于梯形公式的最佳平方逼近样条函数。同样地,当区间左右端点处分别有重节点时,最佳平方逼近函数的具体表达式也可快速求出。 (20) (21) (22) (23) (24) (25) 辛普森公式较梯形公式而言有着更高的代数精度。本节使用辛普森公式做近似求解。 定理3.4设{x0,x1,…,xn}是一组均匀节点,步长为h,β0,β1,β2,β3是P3中一组正交基,则∀f(x)∈C[xi,xi+1],i=0,…,n-1,存在f(x)基于辛普森公式的最佳平方逼近样条函数 (26) 证明:对(βk,f),k=0,1,2,3使用辛普森公式,于是有 从而得到f(x)基于辛普森公式的最佳平方逼近样条函数。证毕。 (27) (28) (29) (30) (31) (32) 图6 均匀节点上的逼近曲线图象Fig.6 An approximation curve image on a uniform node 为方便书写,下文将基于梯形公式的最佳平方逼近和基于辛普森公式的最佳平方逼近分别记为S1,S2。 表1~表4分别求解了四个不同函数基于梯形公式和基于辛普森公式的最佳平方逼近, 并将所求结果与梯形公式和辛普森公式作比较, 可以看出两类最佳平方逼近均具有良好的逼近效果。 表 表 表 表 本文给出了由光滑余因子协调法得到的一元三次B样条基函数,从该函数出发构造了一组新的样条正交基。将该正交基用于求解最佳平方逼近问题,得到了基于梯形公式和基于辛普森公式的最佳平方逼近函数。该结论以非参数形式呈现,表达式简单且便于计算,可直接用于函数逼近计算的相关工作.实验数据表明,该最佳平方逼近函数具有良好的逼近效果。 另外,文章只考虑了一元的情形且未给出具体的逼近误差表达式,后续将考虑能否求解出具体的误差表达式, 同时进一步把文中结论推广到二元,构造二元张量积型正交样条函数,最佳平方逼近的二元样条函数以及计算其逼近误差等。


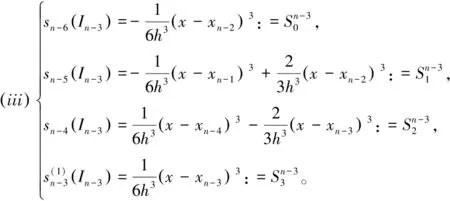


2 基于三次B样条基函数的正交样条基



















3 正交样条的最佳平方逼近
3.1 基于梯形公式的最佳平方逼近样条函数








3.2 基于辛普森公式的最佳平方逼近样条函数








4 数值算例






5 结语

