基于边长约束的凹域三角剖分求破片迎风面积

王佳颖,刘星雨

(1.武警工程大学 基础部， 西安 710086；2.武警工程大学 装备管理与保障学院， 西安 710086；3.上海交通大学海洋智能装备与系统教育部实验室, 上海 200240)

对于不规则形状破片迎风面积(投影区域面积)的计算，通常采用二十面体均匀取向法的光学投影系统试验[1]。该参数可进一步用于破片速度衰减分析、飞散特性研究以及比动能评估[3-7]。为便于自动化计算有限元破片迎风面积并提高求解精度，根据蒙特卡洛剖分投影法建立的平均迎风面积计算模型[8]提出一种最大边长约束的凹域三角剖分算法。该算法以凸包Delaunay三角剖分算法为基础[9-11]，以最大边长约束为原则，对凹多边形区域(简称凹域)边界进行搜索重构，可进一步提高平均迎风面积计算模型的求解精度。目前基于最大边长约束的凹域三角剖分自动化求解破片迎风面积方法，未见相关报道。虽然凸包Delaunay三角剖分算法也可直接用于破片迎风面积的计算，但对于形状不可预知的自然破片而言其误差仍有待进一步分析。

本文根据最大边长约束的凹域三角剖分算法，通过凸包Delaunay三角剖分、剖分边界凹凸性判别、最大边长约束的剖分去除、剖分边界边搜索、边界边排序等步骤，得到任意形状破片投影边界并用于平均迎风面积模型计算。同时，验证并对比了最大边长约束的凹域三角剖分算法与凸包Delaunay三角剖分算法所得平均迎风面积的精度与求解时间。

1 有限元破片

本文以37 mm爆震弹为例[12]，模型采用1/4对称建模，网格大小1 mm×1 mm×2 mm，壳体破碎情况如图1(a)所示。在40 μs时刻壳体已破碎完全，将该时刻各破片单元节点数据导出进行投影剖分。为对比最大边长约束的凹域三角剖分算法与凸包Delaunay三角剖分的迎风面积计算精度与效率，本文重点选择顶部方向、径向、底部方向形状差异较大破片进行求解分析，其具体尺寸形状如图1(b)、图1(c)、图1(d)所示。

2 最大边长约束的凹域三角剖分算法

2.1 算法概述

最大边长约束的凹域三角剖分算法主要包括凸包Delaunay三角剖分、剖分边界凹凸性判别、最大边长约束的剖分去除、凹域边界边搜索、边界边排序5个步骤，其算法流程如图2所示。

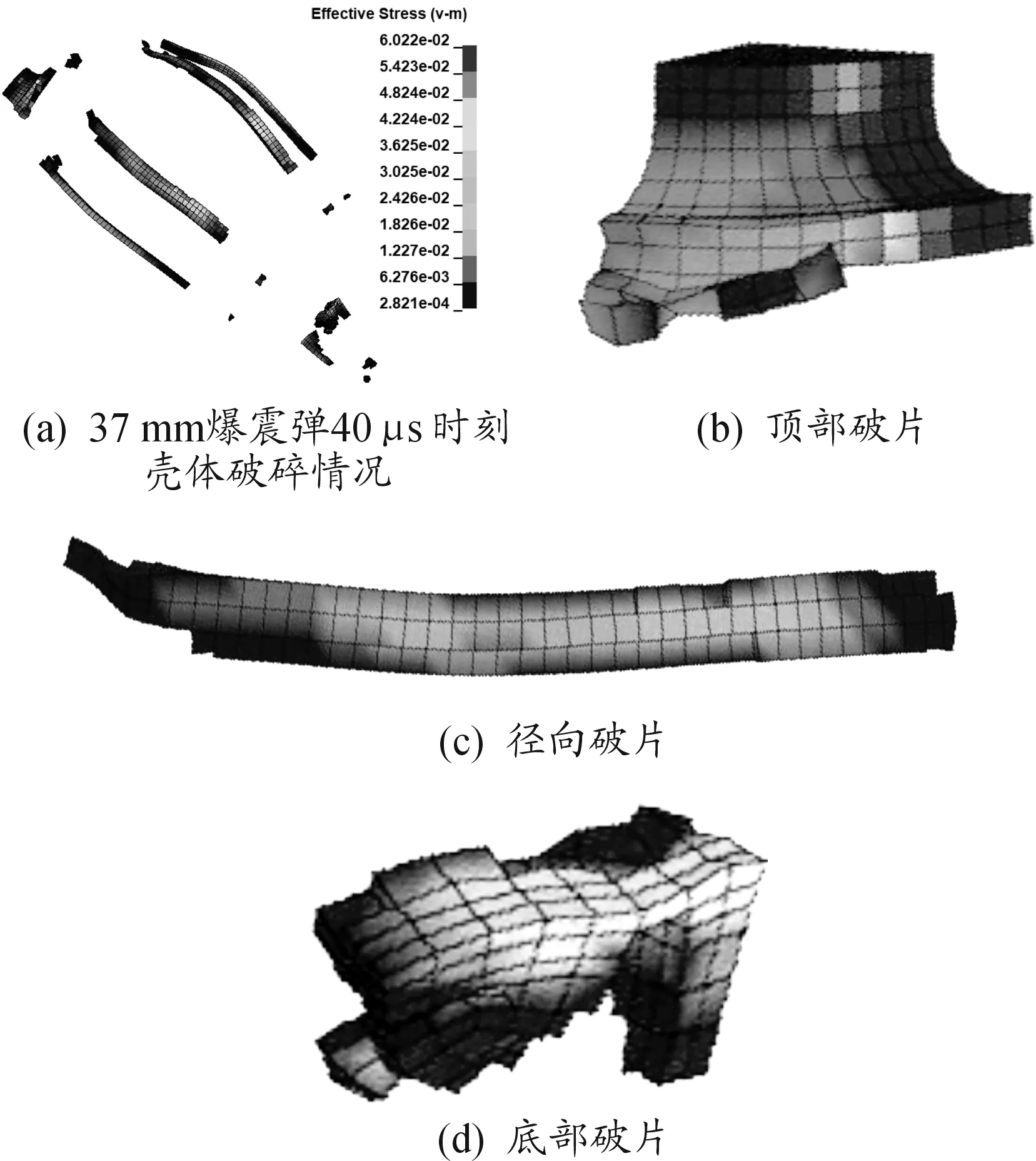
图1 37 mm爆震弹破碎情况及不同方向上的有限元破片

图2 最大边长约束的凹域三角剖分算法流程框图

凸包Delaunay三角剖分根据空外接圆规则可将离散投影节点集T构建成Delaunay三角网，并获得凸包边界dm及三角形矩阵dt_clist；剖分边界凹凸性判别根据凸包三角剖分是否存在大于R的边为原则进行遍历，可提高破片投影为凸包时的计算效率；最大边长约束的剖分去除以不大于凸包三角剖分平均边长的λscale倍为原则，将超出约束边长R的三角边剔除；凹域边界搜索根据公共边、所有边的差集运算，可得到边界边集合；边界边排序根据进栈、出栈的搜索遍历，可得到经排序后的多边形顶点。而后采用叉乘法对任意多边形面积进行求解。

其中，T为无重复节点的投影点集；dm为凸包剖分边界；dt_Clist为凸包三角剖分三角形节点编号；edges为凸包三角剖分升序排列的边界；I为edges中不包含重复边的行号集合；IN为edges的行号集合；IO为边界边行号；sort_vertices用于存放边界顶点序列；polygon为按顺(逆)时针排序的边界边节点坐标。

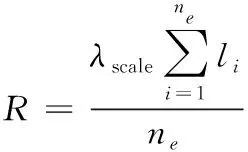
R取值定义如下：

(1)

其中，R为边长约束值；λscale为放大因子；li为剖分三角形第i条边的长度；ne为三角边总数。根据凸包Delaunay剖分空外接圆准则及正六面体有限元节点距离特征，λscale取8～10时可较好地除去非凹域点集的三角边，同时也可避免删除凹域点集内剖分长度较大的有效三角边。本文λscale取8。

2.2 凸包Delaunay三角剖分

当前随机点集的Delaunay三角剖分方法主要有逐点插入法、分治算法、三角组网法等[11]。本文采用改进Bowyer-Watson逐点插入算法，该算法相比于Lawson算法计算效率更高；相比于标准Bowyer-Watson算法，鲁棒性更好。改进的Bowyer-Watson算法通过引入放大因子，可避免标准超级三角形为大钝角时外接圆心落在其外造成剖分边界非凸包的情况。通过判定插入点在待剖分三角形右侧、内侧或外侧位置，分别对剖分三角形进行入栈、再剖分、加入下次剖分等操作，最终可形成满足空外接圆特性和最小角最大化特性的Delaunay三角剖分网格。其算法流程如图3所示。

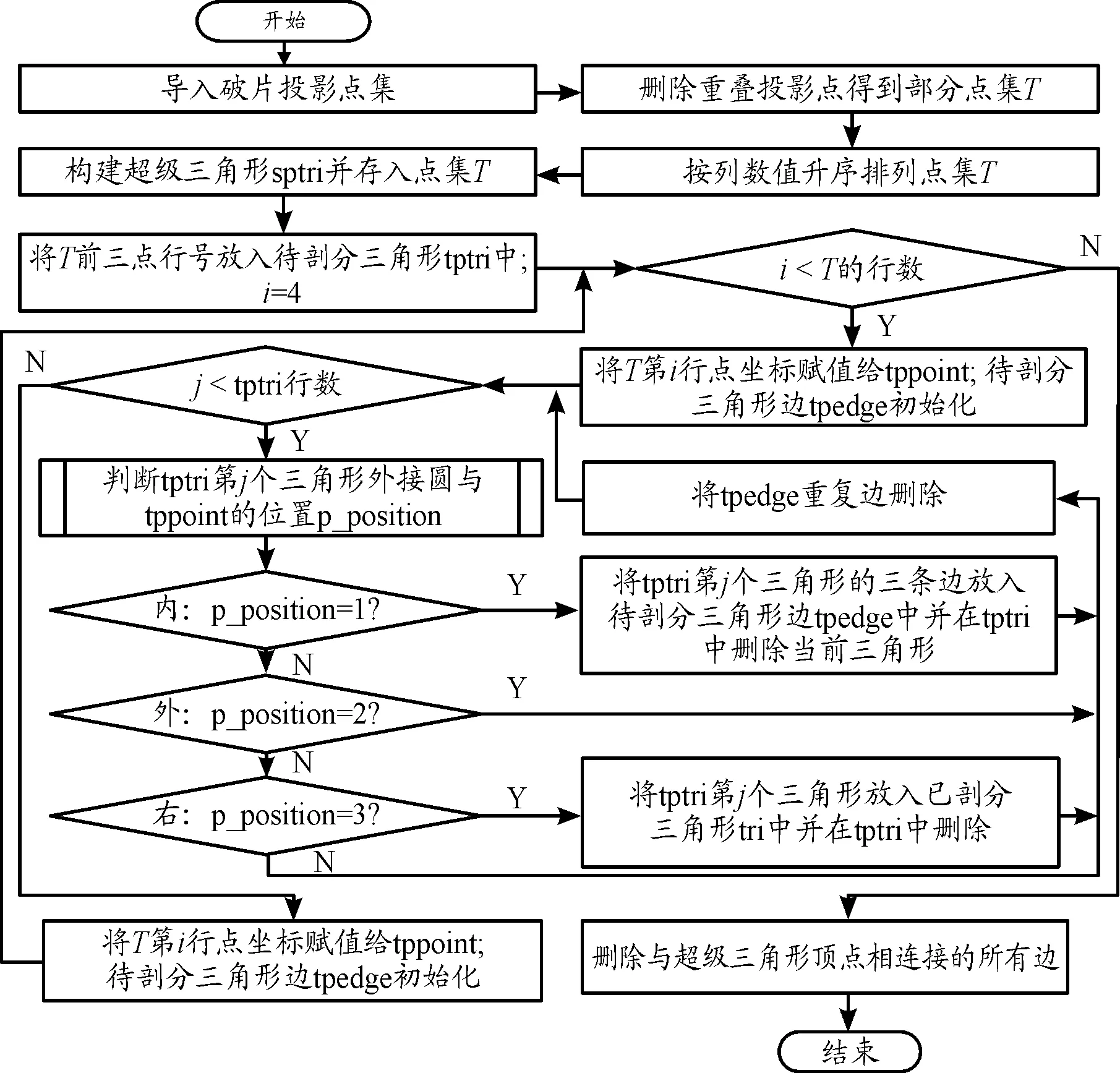
图3 凸包Delaunay三角剖分算法流程框图

判断某点坐标(xi,yi)与三角形外接圆位置，可先根据三角形三顶点坐标(xi-1,yi-1)、(xi-2,yi-2)、(xi-3,yi-3)，求得外接圆圆心坐标(xo,yo)及半径r，而后通过该点与圆心的距离以及与半径之间的关系判定该点位置在圆内侧、圆外侧、圆右侧。外接圆圆心坐标可根据圆上三点至圆心距离两两相等推导得到，表达式如式(2)、式(3)所示。点(xi,yi)与外接圆位置判定表达式如式(4)所示。

(2)

(3)

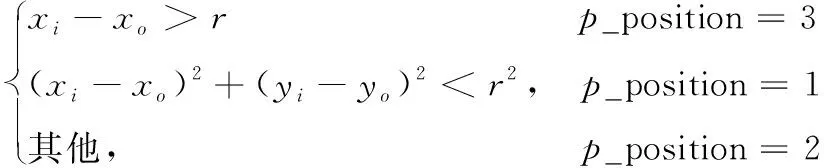
(4)

2.3 凹域边界搜索排序及编程实现

凹域边界搜索的差集运算表达式如式(5)：

EIO=EI-EIN-I

(5)

其中，EIO为凹多边形区域边界边集合，有且仅有一条公共边；EIN-I为凹多边形区域的内部边集合，存在两个公共边；EI为不包含重复边的凹多边形边集合。

凹域边界边搜索与排序的代码如下：

edges数据结构为一行存放一条角边，连续三行为同一三角形；IA为edges中唯一值边对应的行号；通过差集运算可获得边界边点集并存入edges中；sort_vertices拟存放排序后的多边形顶点序号，比当前edges行数多1，确保首尾顶点相连。最终经排序后的凹域边界顶点坐标存入polygon中。

3 结果与讨论

3.1 凹域剖分算法的可行性验证

为验证最大边长约束的凹域三角剖分算法可行性，对图1中的顶部破片、径向破片及底部破片进行求解分析。经过一次投影、凸包三角剖分、带最大边长约束的凹域剖分结果分别如图4(a)、(b)、(c)所示。从图5可知三枚破片形状尺寸差异较大，但通过最大边长约束的凹域三角剖分算法均可得到破片投影图形的边界，并与投影点集吻合较好；凸包Delaunay三角剖分所得边界比投影点集真实边界面积更大。在单次投影结果中，图4(a)中凸包剖分所得面积与凹域剖分面积相差不大，而在图4(b)、(c)中与凹域剖分所得结果则相差较大。由此说明，相比于凸包Delaunay三角剖分算法，最大边长约束的凹域三角剖分算法能更准确地对任意形状破片投影边界进行搜索，可进一步提高自然破片平均迎风面积的求解精度。

3.2 平均迎风面积精度对比

对比3枚破片5 000次投影后所得平均迎风面积结果，两种算法下的迎风面积均值、标准差见表1。

图4 不同方向破片的一次投影、凸包三角剖分、带最大边长约束的凹域剖分结果图

表1 凸包Delaunay算法与最大边长约束的凹域剖分算法均值和标准差

从表1可知：凸包Delaunay算法顶部破片、底部破片标准差均比凹域剖分算法要小，但径向破片标准差更大；凸包Delaunay算法不同方向破片所得迎风面积均值均比凹域剖分算法要大，其中顶部破片、底部破片均值误差相差不大，仅为5.4%和3.6%的差异，但径向破片均值误差可达66.5%。分析造成凸包Delaunay算法各破片均值误差差异较大的原因，主要由各破片形状特征量单元节点与质心距离的标准差决定。对于节点与质心距离标准差较小的顶部、底部破片，其投影图形更加紧凑，使得非凹域点集的无效三角边更少，误差相对变小；而对于距离标准差更大的径向破片，其投影图形更加狭长，使得非凹域点集的无效三角边增多，进而误差显著增大。由此说明，凸包Delaunay算法的平均迎风面积精度受到破片形状特征量影响较大，对于节点与质心距离标准差更小的破片而言凸包算法与凹域剖分算法精度相差较小，而对于节点与质心距离标准差较大的破片精度则相差较大。对自然破片的平均迎风面积求解，采用最大边长约束的凹域剖分算法更能保证计算精度。

3.3 平均迎风面积求解时间对比

为避免CPU时钟的误差影响，选择100次循环所得平均时间作为求解时间，两种算法计算得到的时间见表2。运行环境为Intel (R) Core (TM) i7-8750h CPU @ 2.20 GHz，16 GB，Win10 x64。从表2可知：对于同一算法而言，不同方向的各破片求解时间相差不大，说明两种算法的破片单元数对求解时间并不敏感；而对于同一破片而言，最大边长约束的凹域剖分算法比凸包Delaunay剖分算法求解时间更长，约为30倍。若已知破片形状为凸包或类凸包破片时，可优先选用凸包Delaunay剖分算法进行计算；而对于计算精度优先级高于时效的情况，则选用最大边长约束的凹域剖分算法更为适合。

表2 凸包Delaunay算法与最大边长约束的凹域剖分算法求解得到时间 s

4 结论

基于最大边长约束的凹域三角剖分算法可对任意形状破片的迎风面积进行求解。相比于凸包Delaunay算法，凹域三角剖分算法计算精度更高，但求解时间更长。在已知破片为凸包或类凸包形状时，可优先采用凸包Delaunay算法进行求解。但对于形状未知的有限元破片而言，采用凹域三角剖分算法更为适合。