多层破片战斗部对飞行目标毁伤概率计算方法

薛静云，李翰山，曾 涛

(1.西安工业大学机电工程学院，陕西 西安 710021)

(2.渭南职业技术学院，陕西 渭南 714026)

0 引言

在不确定信息下，破片式战斗部对目标的毁伤效能是评价武器系统研制水平和作战能力的重要指标，利用炸药爆炸驱动多层破片是提高破片式战斗部对目标毁伤的主要途径。如何构建多层破片分布场等特性以及与目标的交汇对抗特性，合理有效地评估多层破片与目标不确定对抗条件下的毁伤效果，一直是目标毁伤评估研究的核心[1-3]。

针对破片毁伤评估的模型方法，文献[4]从战斗部的参数出发，结合导弹的毁伤准则，分析了破片式战斗部对导弹类飞行目标的毁伤概率计算方法；文献[5]根据弹目交会空间关系，随机模拟破片打击射击线，制定了飞行目标易损区域毁伤准则；文献[6]建立了飞机的易损区和毁伤评估模型，得到命中情况下AHEAD弹毁伤目标所需平均命中弹数；文献[7]建立了固定翼飞机在破片打击下的毁伤规律，根据弹目交会和毁伤树模型，评估破片战斗部毁伤效能；文献[8]研究了炮射子母弹毁伤概率近似计算模型，给出了不同形状目标的毁伤概率计算方法。然而，对于多层破片战斗部的参数、弹丸的飞行高度以及飞机目标的易损部位等均存在一定的随机性，很难直接用已有的毁伤评估方法计算[9-11]。本文针对此问题，提出多层破片战斗部对飞行目标毁伤概率的计算方法。

1 多层破片散布密度函数建立

多层破片战斗部爆炸形成的破片可视为动态锥形发散，破片按照不确定的发散角高速运动，在一定的距离处，破片将以一定速度撞击目标，按照破片的质量、速度等形成的动能，对目标进行侵彻毁伤。相对于自然破片战斗部或杆式杀伤战斗部而言，多层破片战斗部要求破片的数量多，战斗部装药量大。在弹道终点目标方位丢失时，自然战斗部破片会出现脱靶，而多层破片战斗部仍具备毁伤能力。

对于多层破片战斗部来说，破片场呈周向对称性分布，考虑多层破片在弹丸轴向速度的影响下，飞散角发生改变，破片飞散示意图如图1所示。

设定战斗部自身飞行速度vm，为了便于计算，假设每层的破片初速相等，且破片静态散布速度为v0，φ为静态飞散角，动态散布条件下的破片初速为vij，飞散角φ′可表示为：

(1)

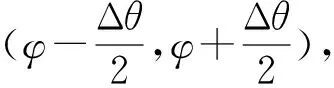
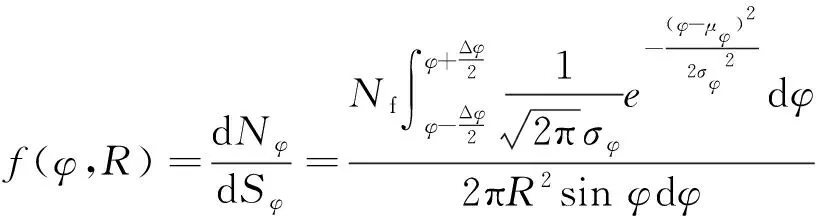
(2)

式(2)中，Nf为战斗部爆炸形成的多层破片总数，它的值是战斗部单层一周的破片数量与轴向层数的乘积；μφ表示飞散角φ数学期望；σφ为飞散角φ的标准差。

动态条件下，战斗部爆炸后在飞散角为φ′，距炸点位置R处破片密度为：

(3)

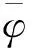
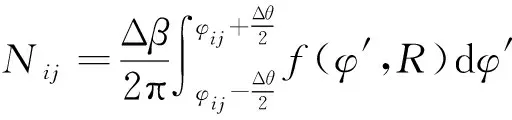
(4)

将一个破片场微元视为一个整体，则整个破片场可以用矩阵Γ表示为：

(5)

2 破片命中目标毁伤概率模型建立

2.1 飞行目标部件毁伤准则

根据飞行目标的易损部件分布不同，将飞行目标分为前机身、驾驶舱、中机身、机翼、后机身五个要害舱段。采用面元法分别对典型飞机的要害舱段几何信息进行描述，飞机易损区域信息如表1所示[13]。

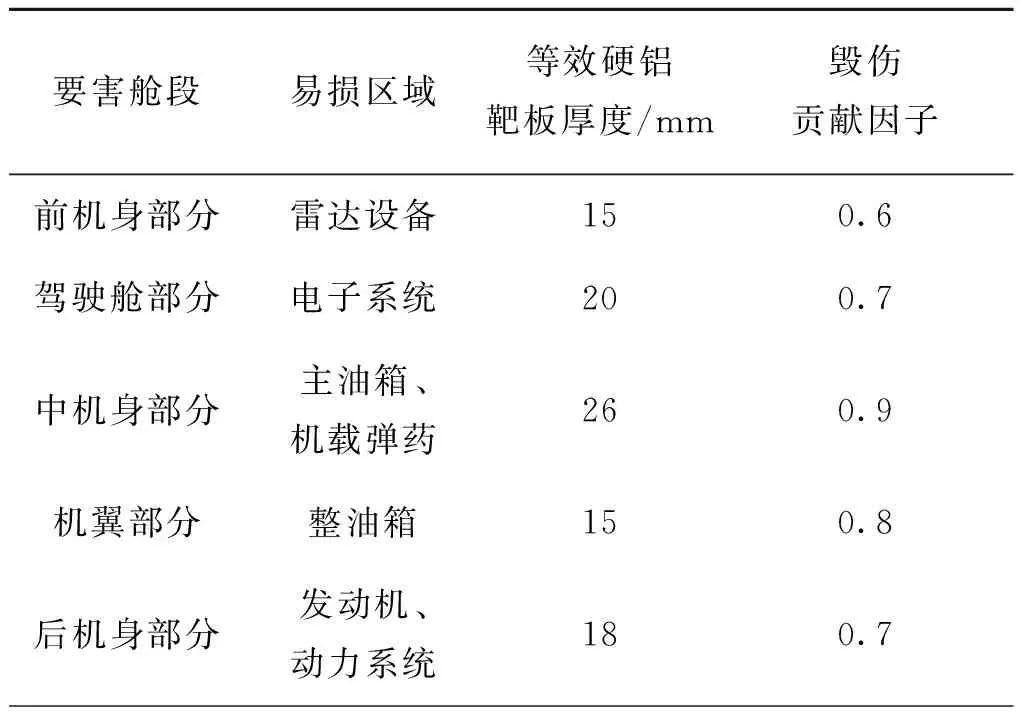
表1 飞机易损区域分类Tab.1 Classification of aircraft vulnerable areas

根据近炸状态下破片的散布特性，设定多层破片飞行距离R(t)后击中目标时的临界速度为：

(6)

式(6)中，cx为空气阻力系数，ρ0为空气密度，m为破片质量。破片对飞行目标的毁伤效能用破片的极限穿透速度表示，如果破片的飞行速度大于极限穿透速度，该破片为有效破片，否则为无效破片。破片对目标的极限穿透速度可表示为：

(7)

式(7)中，b0为飞行目标易损区域等效硬铝靶板厚度；d为球形破片直径(每个破片认为是一个球体)；ρσ为破片材料的密度；ρt为硬铝靶板密度；kτ为硬铝靶板极限强度;a，b为经验系数。当破片击中目标时的相对速度达到vR≥vL时，则认为该破片为有效破片，对飞行目标产生毁伤效能[14]。

2.2 目标毁伤概率计算方法

在研究目标毁伤概率时，不同战斗部炸点位置对应不同的弹目交会方式[15]。假设破片场均匀散布，则破片场飞行R(t)距离后，则破片场的整体毁伤区域面积可以表示为：

SP=R(t)2π(tanφmax′2-tanφmin′2)。

(8)

由于破片的随机性和不确定性，破片式战斗部存在盲区等因素带来的影响，采用有效破片命中飞行目标的毁伤面积与战斗部的整体毁伤区域面积的比值来表示破片式战斗部的毁伤增益。假设预制圆形破片的半径为r，则破片式战斗部的毁伤增益G可以表示为：

(9)

判断破片微元命中飞行目标要害舱段的情况，可表示为矩阵：

(10)

式(10)中，km为破片束微元与飞行目标第m个要害舱段的命中判断矩阵，若轴向第i个周向第j个破片束微元命中飞行目标第m个要害舱段，则kmij=1，否则kmij=0。

则整个破片场命中目标第m个要害舱段的破片数目为：

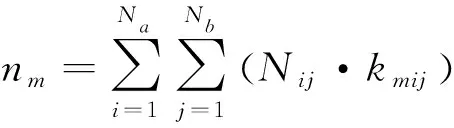
(11)

破片群对第m类要害舱段的毁伤概率可表示：

Pm=1-(1-Gpe)nm，

(12)

式(12)中，Pe为破片击穿概率，nm为破片声命中目标第m个要害舱段的破片数量。

3 算例计算与仿真分析

设置破片式战斗部装填直径为5 mm、层数为4的球形破片，破片动态飞散角度区间为[5°，25°]；假设战斗部飞行速度为220 m/s，飞行目标飞行速度为100 m/s，双方以迎击的姿态匀速运动，分析多层破片战斗部在不同炸点对飞行目标毁伤概率的影响。将飞行目标设定为F-15战斗机，结构参数如表2所示。

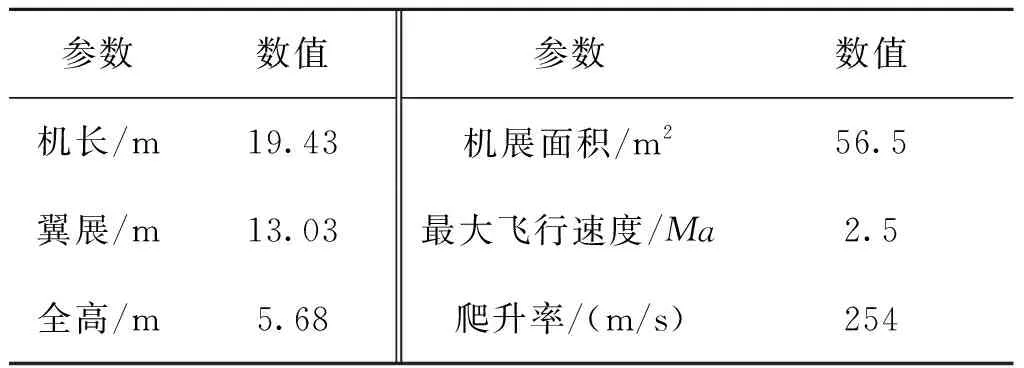
表2 F-15机体结构参数Tab.2 Structure parameters of F-15 body

以飞行目标中心为原点，结合多层破片散布规律随机散点，则破片命中数量随破片飞行距离变化的如图2所示。

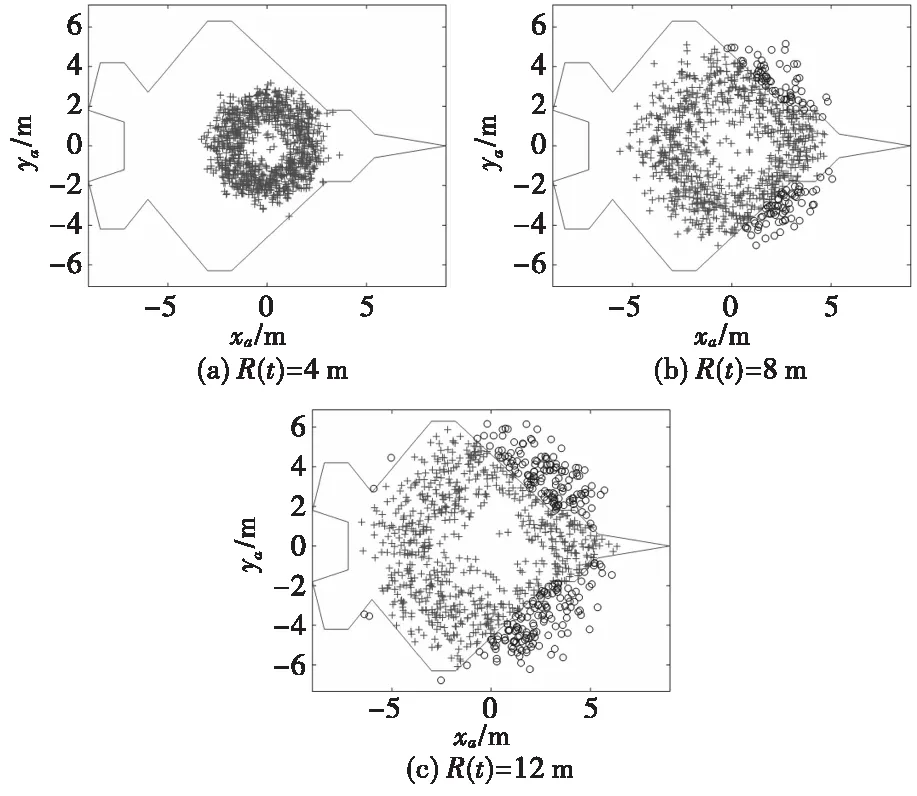
图2 破片命中数量随飞散距离变化仿真图Fig.2 The number of fragment hits varies with the flying distance

可以得出在一定的破片动态飞散角度区间内，破片飞散距离与破片命中飞行目标范围相关：当飞散距离较小时，破片场散布范围较为集中，导致破片场命中飞行目标要害舱单范围较小；当飞散距离较大时，破片场较为分散，基本可以覆盖整个飞行目标，但是命中飞行目标的破片数目有所下降。

通过式(10)的破片命中飞行目标要害舱段矩阵，将飞行目标各舱段按照毁伤贡献因子由高到低划分为面积均等的四部分A、B、C、D，在均匀的破片散布密度和相同破片侵彻速度条件下，计算破片数量与飞行目标要害舱段的毁伤概率分布，仿真计算结果如图3所示。

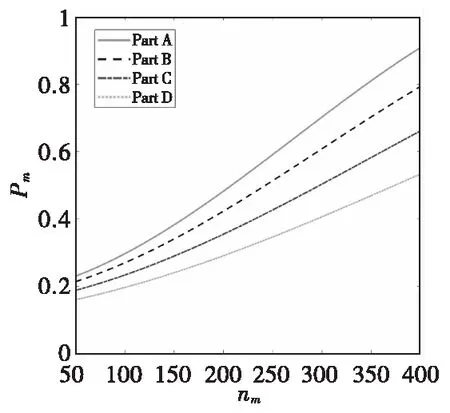
图3 破片数量与飞行目标要害舱段毁伤的变化关系Fig.3 The relationship between the number of fragments and the damage of the flying target critical compartment

结果表明，破片命中飞行目标要害舱段的数量与飞行目标要害舱段毁伤概率成正比，特别是在毁伤贡献因子较大的要害舱段；飞行目标要害舱段呈现面积一定的条件下，破片毁伤叠加面积增大，即破片式战斗部毁伤增益变大。

同时，在参数不变的情况下，分析多层破片动态飞散角度区间对飞行目标整体毁伤概率的影响，如图4所示。

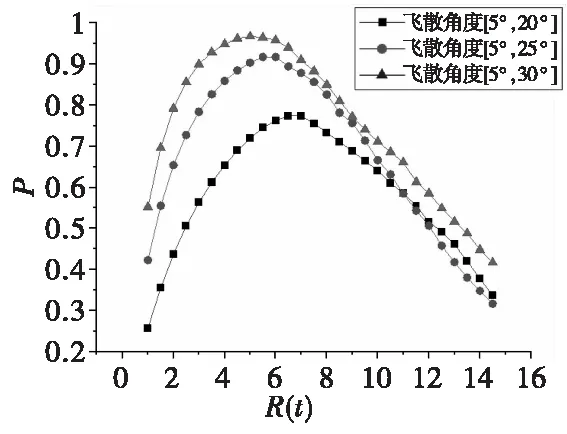
图4 不同飞散角度区间对飞行目标毁伤概率的影响Fig.4 The influence of different dispersion angles on the flying targets damage probability

结果表明，在一定的破片飞散距离下，破片飞散角度区间同飞行目标毁伤概率成正比；同时，随着破片飞散距离增加，飞行目标毁伤概率开始降低。

4 结论

本文从多层破片飞散特性和目标毁伤准则出发，建立了一种飞行目标毁伤概率计算方法。进行了定量分析和仿真计算，得到如下结论：

1) 在破片动态飞散角度区间固定的条件下，随着破片飞散距离增加，会使得破片场散布范围变大，但是破片有效命中面积范围会先增加后减小；

2) 破片命中飞行目标要害舱段的数量与飞行目标要害舱段毁伤概率成正比，特别是在毁伤贡献因子较大的要害舱段，这种增长趋势更加明显；

3) 在一定的破片飞散距离下，破片飞散角度区间同飞行目标毁伤概率成正比，破片飞散距离同飞行目标毁伤概率成反比。

本文建立的多层破片式战斗部对目标毁伤概率计算方法，为打击飞行目标的设计提供了理论支撑。