不同阶曲线拟合扰动场对下平流层重力波气候特征影响研究*
程胡华 王益柏 武 帅 赵 亮 智茂林
1.63729 部队,太原,030027
2.61741 部队,北京,100094
3.32021 部队,北京,100094
4.中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室(LASG),北京,100029
1 引 言
重力波对全球大气的动力、热力结构变化及调整具有重大影响(Holton,1983;Fritts,et al,2003),与多种不同尺度天气现象均有密切联系。中外研究均表明,大气重力波影响着台风(洪军等,2015;陈丹等,2011;Chen,et al,2013)、雨雪(邓少格等,2012;程胡华,2016;孙艳辉等,2015)、冰雹(李启泰等,1993;覃卫坚等,2010)等其他天气(Thomas,et al,1999;林永辉等,2003;陈丹等,2014;Plougonven,et al,2014;Kramer,et al,2015;李驰钦等,2018)的产生、发展和消亡;因此,为提高大气模式对不同尺度天气现象的预报能力,需要在大气模式中使用重力波参数化的方法加入重力波影响(徐国强等,2010;王宇虹等,2017),利用高垂直分辨率探空资料获取全球范围内大气重力波参数气候特征及其分布,已成为研制大气模式中重力波参数化方案的重要前提条件之一(Yamamori,et al,2006;Zhang,et al,2010)。
20世纪80年代,科学家们使用无线电探空资料中的温度廓线研究重力波能量及谱斜率(van Zandt,1982),随后,Kitamura等(1989)、Hamilton(1991)、Allen等(1995)利用风场、温度场廓线计算重力波参数,经过不断的完善(Eckermann,1996;Eckermann,et al,1999),形成了依据风场和温度场廓线计算重力波参数的一套完整方法,该方法已被认可并广泛应用(Guest,et al,2000;卞建春等,2004;Zhang,et al,2005,2007;Ki,et al,2010;白志宣 等, 2016;Kafando, et al, 2016; Marlton,et al,2016;Jackson,et al,2018;Chen,et al,2019;吴泓锟等,2019)。在利用此方法获取大气重力波参数时,首先需获取温度场、纬向风和经向风的垂直扰动场,目前,不同阶曲线拟合法是获取扰动场的常用方法(Guest,et al,2000;卞建春等,2004;Zhang,et al,2005,2007;Ki,et al,2010;白志宣等,2016;Kafando,et al,2016;Marlton,et al,2016;Jackson,et al,2018;Chen,et al,2019;吴泓锟等,2019),例如,白志宣等(2016)利用2阶曲线拟合法得到中国南北向8个站两年多高垂直分辨率无线电探空资料下平流层扰动场,基于该扰动场获取下平流层惯性重力波,并对该重力波活动的季节变化及其随纬度分布特征进行研究;Ki等(2010)基于韩国10个站高垂直分辨率探空资料,通过3阶曲线拟合扰动场获取下平流层大气重力波参数,并对重力波源及其特征进行研究;Guest等(2000)利用4阶曲线拟合扰动场获取麦夸里岛下平流层重力波参数,并对重力波参数的季节变化及波源特征进行了研究。
目前,不同阶曲线拟合扰动场获取的重力波参数气候特征是否与实况一致,尚未得到大量观测资料或实验方法的有效验证,且针对不同阶曲线拟合扰动场之间的差异特征并分析依此计算得到大气重力波参数间气候差异特征的研究较少,程胡华等(2013,2016)利用Morlet小波对不同阶曲线拟合扰动场进行分析发现,大多数情况下扰动场中包含背景场信号,其含有的背景场信号强弱对大气重力波参数有较大影响;程胡华(2017)以2013年8月6—8日晋西北地区出现的一次雷阵雨天气过程为例,利用不同方法获取高垂直分辨率探空资料扰动场,发现所得扰动场垂直廓线之间存在一定差异,该差异对获取大气重力波参数的大小及变化趋势存在影响,但对不同重力波参数的影响程度不同;文中在已有研究(程胡华等,2013,2016;程胡华,2017)的基础上,利用2014—2017年太原地区高垂直分辨率探空资料,进一步针对不同阶曲线拟合扰动场对下平流层(17—24 km高度)大气重力波参数气候特征的影响进行统计研究。
2 资料及计算方法
所用研究资料为山西太原气象台(37.78°N,112.55°E)提供的2014—2017年高垂直分辨率探空资料,每日08时(北京时)的温度、湿度和气压的垂直分辨率约为10 m,风速的垂直分辨率约为300 m,由于原始资料的垂直间隔不等,在此利用3次样条插值方法得到垂直分辨率为50 m的气象要素值。
对于高垂直分辨率探空资料中的纬向风速(u)、经向风速(v)、温度(T),由于对流层和平流层大气间的浮力频率差异较大,并且为了避开对流层顶的极低温度和对流层上部纬向风急流的影响,选择下平流层高度范围为海拔17 —24 km(马兰梦等,2012);分别采用2—4阶曲线拟合法得到下平流层背景场(u¯、v¯ 、T¯ ),用原始数据(u、v、T)减去背景场(u¯、v¯ 、T¯ ),即得到扰动场(u′、v′、T′)。获取重力波参数所用的程序包为澳大利亚阿德莱德大学R.Vincent教授提供,线性重力波理论(卞建春等,2004;邓少格等,2012;Sawyer,1961)和多种观测资料均表明,由重力波产生的水平风速矢量(u′(z),v′(z))端点的连线,大致表现为椭圆形状,若重力波的水平传播方向为自北顺时针旋转角度(α),则 α方向即为水平风扰动矢量偏振椭圆的长轴方向(卞建春等,2004;邓少格等,2012;Hines,1989)。通过利用 Stokes参数(卞建春等,2004;邓少格等,2012;Eckermann,1996)和主成分分析法(卞建春等,2004;邓少格等,2012),借助Hilbert变换后的归一化温度扰动和速度扰动分量的关系(卞建春等,2004;邓少格等,2012),可确定出重力波水平传播方向(φ)、椭圆偏振度(d)和偏振椭圆的长短轴,由偏振椭圆长短轴之比(卞建春等,2004;邓少格等,2012),即可求出波固有频率()和固有周期通过归一化温度扰动()的垂直波数功率谱可以估算出波动的垂直波数(m)(Hoffmann,et al, 2006; Moffat-Griffin, et al,2011),依据波数与波长的关系,可求取垂直波长(λz, λz=2π/m),将上述得到的和m代 入由线性重力波理论得到的频散关系式,可得到重力波的水平波长(λh)、固有相速(ci)、对地水平群速(cg)等一系列的波参数。
基于最新研究成果(白志宣等,2016;Jackson,et al,2018;Chen,et al,2019;吴泓锟等,2019)采用2阶曲线拟合扰动场,程胡华(2017)研究发现,利用2阶曲线拟合扰动场获取大气重力波参数的演变特征,与2013年8月6—8日的大气动力演变特征基本吻合,故以2阶曲线拟合扰动场及计算得到的重力波参数为基准,统计其与其他阶曲线拟合扰动场的相关系数,并对相关系数在不同区间内的占有率进行统计,随后对计算得到的重力波参数间的相关、偏差特征及占有率进行统计分析,其中,占有率为物理量数值在某区间内的个数占总数的百分比。
3 扰动场特征对比
记Rank2、Rank3、Rank4分别代表2阶、3阶、4阶曲线拟合的扰动场,Upert、Vpert、Tpert分别为纬向风扰动场、经向风扰动场、温度扰动场。表1列出了2—4阶曲线的拟合优度(Goodness of Fit)参数值统计结果,其中,参数 SSE (The sum of squares due to error) 、 RMSE (Root mean squared error)、R2(Coefficient of determination)、Radj(Degree of freedom adjusted coefficient of determination)分别表示误差平方和、均方根误差、决定系数、自由度调整决定系数,SSE和RMSE值越小、R2和Radj值越接近1,表明曲线拟合优度越高,从表1可以看出,4阶曲线的拟合优度最高,其次为3阶曲线拟合方法,而2阶曲线拟合方法的拟合优度较差。
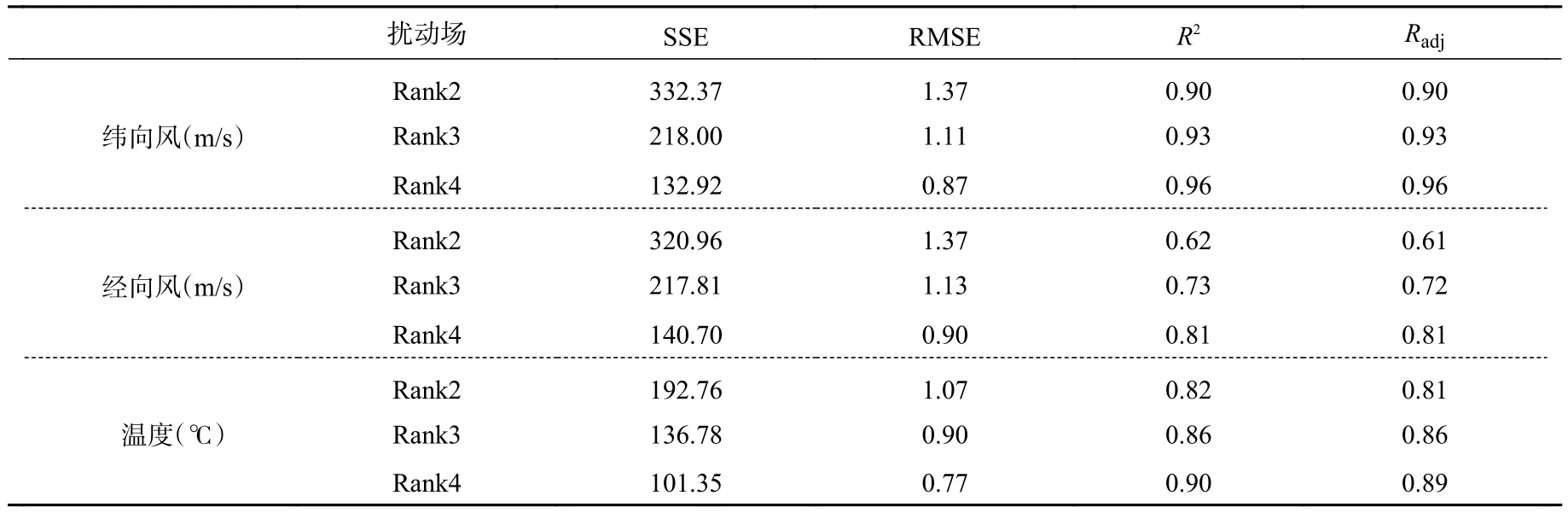
表1 2—4 阶曲线的拟合优度参数值统计结果Table 1 Statistical results of goodness of fit parameter values for 2—4 degree curve fitting
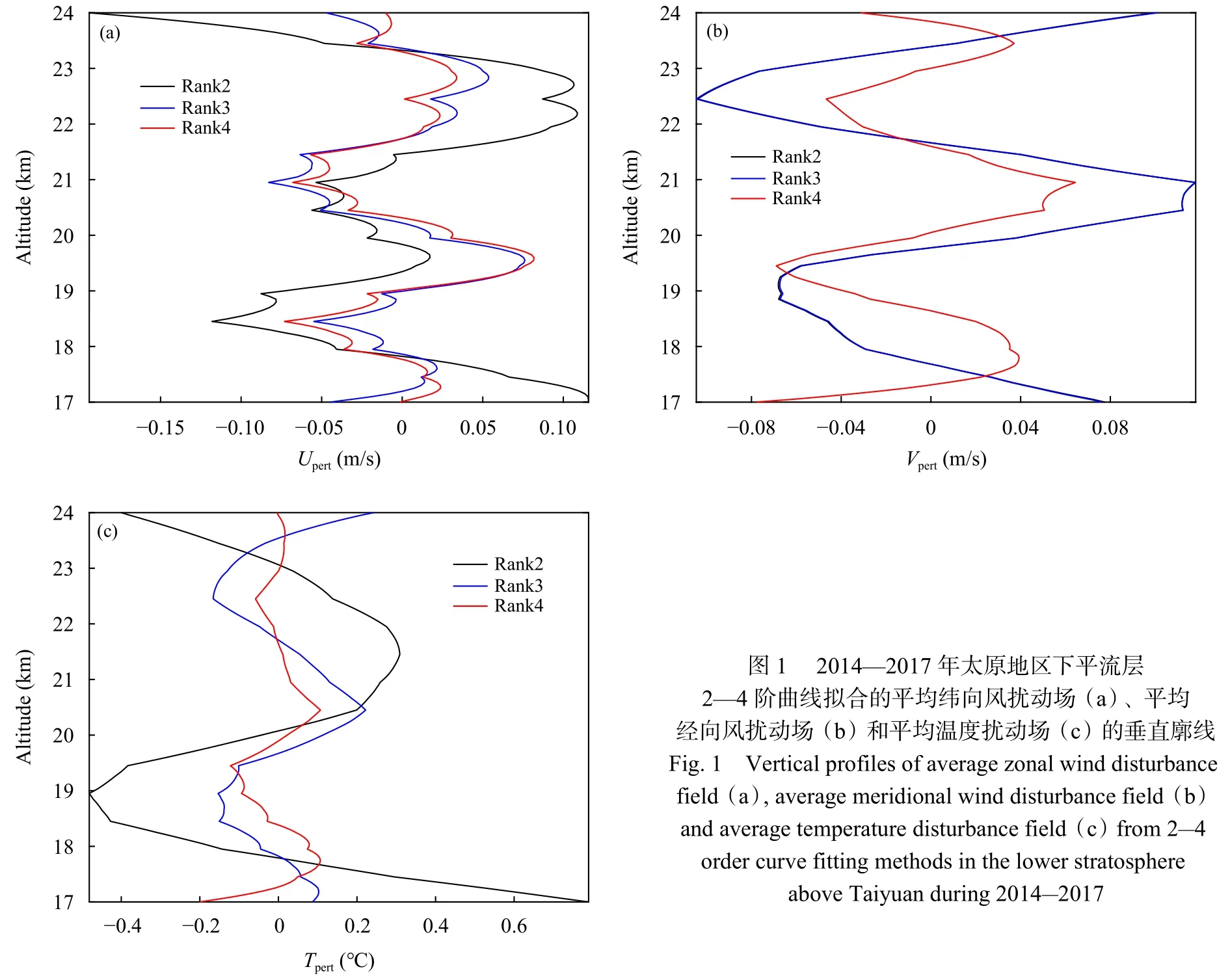
从2014—2017年太原地区下平流层(17—24 km)2—4 阶曲线拟合得到的Upert、Vpert、Tpert随高度变化特征(图1)可见,平均纬向风扰动场随高度变化趋势基本一致,但振幅存在一定差异(图1a),在整个高度范围内,2—4阶平均纬向风扰动场范围分别为 −0.19 (24.00 km) — 0.12 m/s (17.00 km) 、−0.08(20.95 km)—0.08 m/s (19.55 km)和−0.07(18.45 km)—0.08 m/s (19.60 km),2 阶与 3 阶平均经向风扰动场随高度变化基本重合,但在高度17—18、23—24 km均与4阶扰动场的变化趋势相反(图1b),在高度 17—24 km,2—4 阶平均经向风扰动场范围分别为−0.10 (22.45 km)—0.12 m/s(20.95 km)、−0.10 (22.45 km)—0.12 m/s (20.95 km)和−0.08 (17.00 km)—0.06 m/s (20.95 km),2—4 阶平均温度扰动场之间的振幅及随高度变化特征均存在一定差异(图1c),其中,2阶平均温度扰动场振幅明显偏大,在高度17—24 km,2—4阶平均温度扰动场范围分别为−0.48 (18.95 km)—0.79℃(17.00 km)、−0.17(22.45 km)—0.24℃ (24.00 km)和−0.20 (17.00 km)—0.11℃ (20.45 km)。
为反映不同阶曲线拟合扰动场间的相关,通过计算每个时次的3阶、4阶曲线拟合与2阶曲线拟合扰动场垂直廓线的相关系数,得到2014—2017年样本数的数组;图2给出3阶、4阶曲线拟合与2阶曲线拟合的纬向风扰动场的相关系数、经向风扰动场相关系数、温度扰动场相关系数在不同区间内占有率的分布特征,除相关系数在[0.0,0.1]内占有率均为0外,在其他区间占有率均大于0,其中,3阶曲线拟合扰动场相关系数值沿横坐标均呈现出增大特征,而4阶曲线拟合扰动场相关系数值沿横坐标呈现出增大、基本维持不变的趋势特征。3阶、4阶曲线拟合纬向风扰动场相关系数分别在(0.9,1.0 ]、(0.7,0.8 ]内占有率最大(图2a),分别为45.46%和16.54%,相关系数超过0.8的占有率分别为62.54 %和27.38%,而相关系数不超过0.5的占有率分别为5.31%和22.31%,类似纬向风扰动场相关系数分布特征,3阶、4阶曲线拟合经向风扰动场相关系数分别在(0.9,1.0]、(0.8,0.9]内占有率最大(图2b),分别为45.46%和17.77%,相关系数超过0.8的占有率分别为65.38%和30.23%,相关系数不超过0.5的占有率分别为4.31%和18.69%,3阶、4阶曲线拟合温度扰动场相关系数均在(0.9,1.0]内的占有率最大(图2c),分别为47.62%和20.46%,而相关系数超过0.8的占有率分别为67.54%和40.08%,相关系数不超过0.5的占有率分别为2.31%和9.46%。
从上述分析可知,与4阶曲线拟合扰动场相比,2阶与3阶曲线拟合扰动场的相似度更高;因此,下面针对2阶、3阶曲线拟合扰动场获取的下平流层大气重力波参数结果进行对比研究。
4 重力波参数特征对比
4.1 群 速
2阶、3阶曲线拟合扰动场的群速值范围、年内变化趋势存在一定差异(图3a),2—5月,2阶曲线拟合扰动场的群速表现为增大、减小、增大的变化特征,而 3阶曲线拟合扰动场的群速表现为减少、增大的变化特征;7—9月,2阶曲线拟合扰动场的群速表现为减小、增大的变化特征,而3阶曲线拟合扰动场的群速为一致减小;1—12月,2阶曲线拟合 扰 动 场 的 群 速 值 为 −1.52(12月 ) — 8.97 m/s(7月),平均值为 3.51 m/s,1月、11—12月为负值;而3阶曲线拟合扰动场的群速为−3.64(12月)—7.30 m/s(7 月),平均为 2.10 m/s,1 月、10—12 月为负值;2阶与3阶曲线拟合扰动场之间的群速相关系数年内变化特征(图3b)可见,除4月超过0.8外,其他月份的群速相关系数均小于0.8,1—12月,群速相关系数的值为 0.57(6月)—0.81(4月),平均为0.71。
2阶、3阶曲线拟合扰动场的群速在不同区间内占有率分布特征(图4)可见,不同区间占有率沿横坐标均呈现出增大、减小的变化,其最大值位于[0,10)(图4a),分别为 40.05%、43.35%,而在(−∞,−20]、[30,+∞)内的占有率均较小,合计分别为1.65%、1.65%;3阶与2阶曲线拟合扰动场之间的群速偏差(以2阶曲线拟合扰动场的群速为基准,下同)在不同区间内占有率的分布特征(图4b)表明,其占有率最大值出现在[−10,0),数值为56.88%,主要出现在 [−0,10),占有率为90.87%,而在其他区间内的占有率不超过10%,合计为9.13%。
4.2 水平波长
2阶、3阶曲线拟合扰动场的水平波长及水平波长相关系数的年内变化特征(图5)表明,1—12月,2阶曲线拟合扰动场的水平波长均明显大于对应的3阶曲线拟合扰动场(图5a),2阶、3阶曲线拟合扰动场的水平波长最大值均出现在8月、最小值均出现在12月;1—3月,2阶曲线拟合扰动场的水平波长呈现出增大、减小的变化特征,而3阶曲线拟合扰动场的水平波长为一致减小;6—8月,2阶曲线拟合扰动场的水平波长表现为减小、增大的变化特征,而3阶曲线拟合扰动场的水平波长为一致增大;1—12月,2阶曲线拟合扰动场的水平波长范围为 279.37 (12 月)—444.55 km (8 月),平均为346.36 km,而3阶曲线拟合扰动场的水平波长范围为 217.07(12月)—306.93 km(8月),平均为261.83 km;2阶与3阶曲线拟合扰动场之间的水平波长相关系数年内变化(图5b)表明,1—12月,水平波长相关系数范围为0.28(6月)—0.74(11月),平均值为0.55。
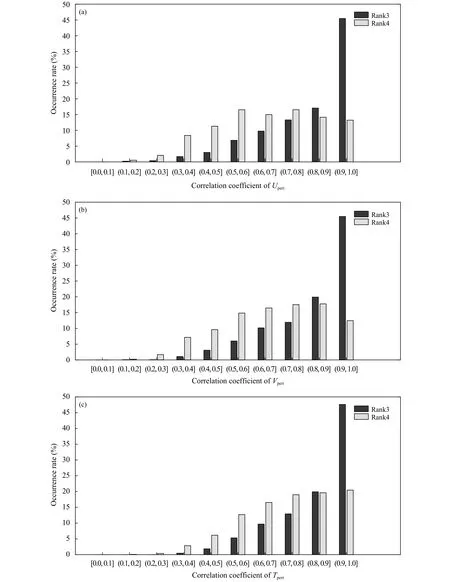
图2 2014—2017年太原地区下平流层 3阶、4阶曲线拟合与2阶曲线拟合的纬向风扰动场相关系数 (a)、经向风扰动场相关系数 (b) 和温度扰动场相关系数 (c) 的分布Fig.2 Distribution characteristics of zonal wind disturbance field correlation coefficient (a),meridional wind disturbance field correlation coefficient (b) and temperature disturbance field correlation coefficient (c) between 3rd,4th order curve fitting methods and 2nd order curve fitting method in the lower stratosphere above Taiyuan during 2014—2017
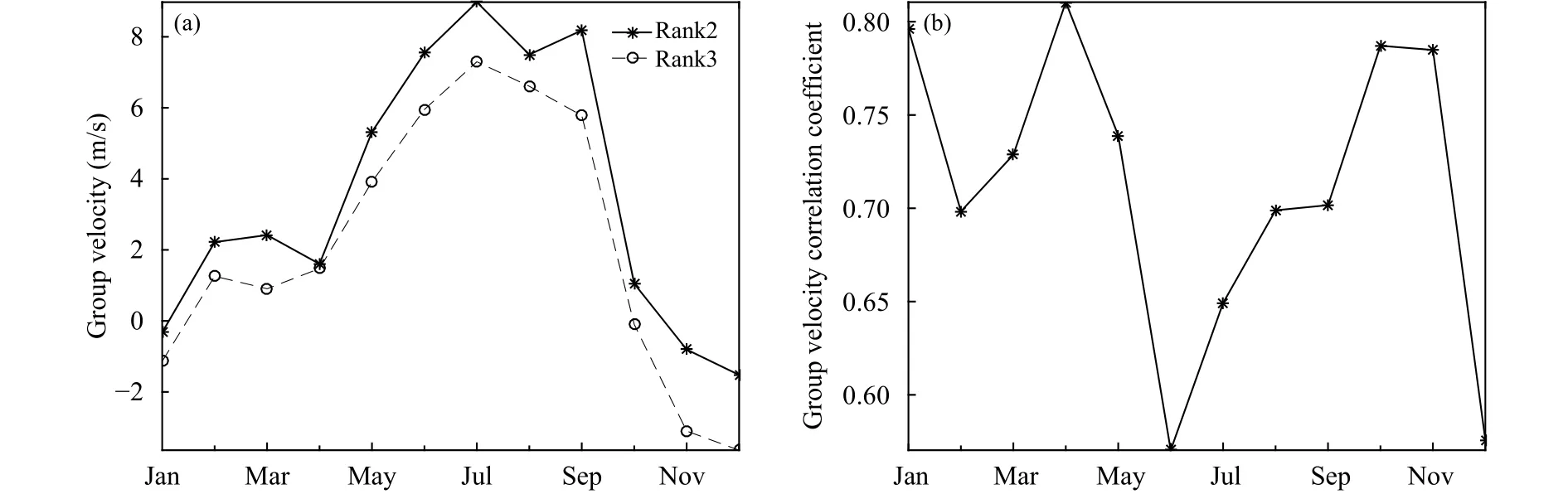
图3 2014—2017 年太原地区下平流层 3 阶与 2 阶曲线拟合扰动场的群速值 (a) 和群速相关系数 (b) 的月变化Fig.3 Annual variations of group velocity from disturbance fields obtained by second and third order curve fitting (a) and group velocity correlation coefficient (b) in the lower stratosphere above Taiyuan during 2014—2017

图4 2014—2017年太原地区下平流层3阶与2阶曲线拟合扰动场的群速 (a)和群速偏差(b)在不同区间占有率的分布Fig.4 Occupancy distribution characteristics of group velocity from disturbance fields obtained by second and third order curve fitting (a) and group velocity deviation (b) in different interval ranges in the lower stratosphere above Taiyuan during 2014—2017
2阶、3阶曲线拟合扰动场的水平波长在不同区间内占有率沿横坐标方向呈现出减小趋势,但最大值均未超过 50 %(图6a),且均在(0,200)占有率最高,分别为 39.50 % 和 49.72 %,其次为 [200,400),分别为 28.56%和 28.64%,而在 [600,800)、 [800,+∞)内的占有率均小于10%。3阶与2阶曲线拟合扰动场间的水平波长偏差在不同区间内的占有率分布特征(图6b)表明,其在 [−200,0)内占有率最高(42.64%),主要出现在[−200,200],占有率为73.09%,而在 [200,+∞)内占有率为 6.06%,在(−∞,−200)内占有率为20.85%。
4.3 垂直波长
2阶、3阶曲线拟合扰动场的垂直波长及垂直波长相关系数的年内变化特征(图7)表明,1—12月,2阶曲线拟合扰动场的垂直波长均大于对应的3阶曲线拟合扰动场(图7a),2—4月,2阶曲线拟合扰动场的垂直波长为一致减小,而3阶曲线拟合扰动场的垂直波长表现为减小、增大变化特征,5—7月,2阶曲线拟合扰动场的垂直波长为一致增大,而3阶曲线拟合扰动场的垂直波长表现为减小、增大变化特征;1—12月,2阶曲线拟合扰动场的垂直波长范围为 2.64(5月)—2.94 km(12月),平均为2.76 km,3阶曲线拟合扰动场的垂直波长范围为2.20(6月)—2.55 km(12月),平均为 2.38 km;2阶与3阶曲线拟合扰动场垂直波长的相关系数年内变化特征(图7b)表明,1—12月,垂直波长相关系数范围为 0.56(6月)—0.86(1月),平均为 0.72。
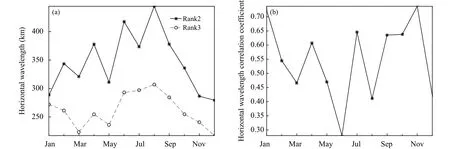
图5 2014—2017 年太原地区下平流层 3 阶与 2 阶曲线拟合扰动场的水平波长 (a)和水平波长相关系数 (b) 的月变化Fig.5 Annual variations of horizontal wavelength from disturbance fields obtained by second and third order curve fitting (a) and horizontal wavelength correlation coefficient (b) in the lower stratosphere above Taiyuan during 2014—2017
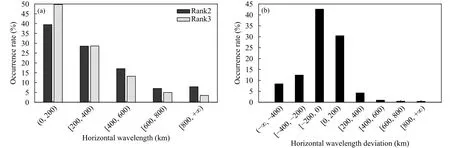
图6 2014—2017 年太原地区下平流层 3 阶与 2 阶曲线拟合扰动场的水平波长 (a) 和水平波长偏差 (b) 在不同区间占有率的分布Fig.6 Occupancy distribution characteristics of horizontal wavelength from disturbance fields obtained by second and third order curve fitting (a) and horizontal wavelength deviation (b) in different interval ranges in the lower stratosphere above Taiyuan during 2014—2017
2阶与3阶曲线拟合扰动场的垂直波长及其之间的垂直波长偏差,在不同区间内占有率的分布特征(图8)表明,其占有率沿横坐标方向呈现出增大、减小的变化特征(图8a),最大值均出现在[2,3),分别为50.67%和60.19%,其次分别出现在 [3,4)和[1,2),分别为 32.02% 和 26.51%,而在(0,1)内均为0,且3阶曲线拟合扰动场的垂直波长在 [4,+∞)占有率为0,而相应的2阶曲线拟合扰动场垂直波长为4.09%;垂直波长偏差在不同区间内的占有率分布特征如图8b所示,其占有率沿横坐标轴方向呈现出增大、减小的变化特征,且在 [−1,0)内占有率最大(70.97%),在 [0,1)占有率为次大(18.57%),而在 [1,+∞)、(−∞,−3)占有率均为 0.00%。
4.4 周期
2阶、3阶曲线拟合扰动场的周期及周期相关系数的年内变化(图9)表明,1—12月,2阶曲线拟合扰动场的周期值均大于对应的3阶曲线拟合扰动场,且两者年内变化趋势基本一致,均呈现出增大、减小的趋势(图9a),1—12月,2阶曲线拟合扰动场的周期为6.20(12 月)—8.80 h(8 月),平均为7.4012 h,3阶曲线拟合扰动场的周期值范围为5.68(12月)—7.92 h(6 月),平均为 6.86 h;2 阶与 3 阶曲线拟合扰动场的周期相关系数1—12月的变化范围为 0.38(6月)—0.75(1月),平均为 0.63(图9b)。

图7 2014—2017 年太原地区下平流层 3 阶与 2 阶曲线拟合扰动场的垂直波长 (a) 和垂直波长相关系数 (b) 的月变化Fig.7 Annual variations of vertical wavelength from disturbance fields obtained by second and third order curve fitting (a) and vertical wavelength correlation coefficient (b) in the lower stratosphere above Taiyuan during 2014—2017
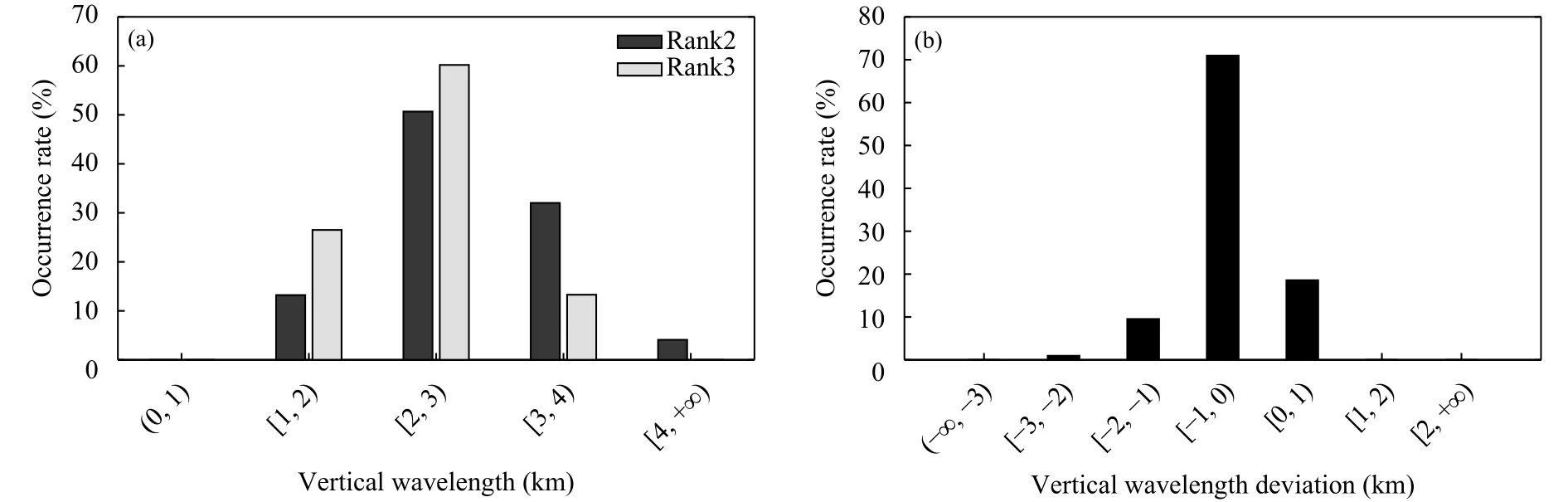
图8 2014—2017 年太原地区下平流层 3 阶与 2 阶曲线拟合扰动场的垂直波长 (a) 和垂直波长偏差 (b) 在不同区间的占有率Fig.8 Occupancy distribution characteristics of vertical wavelength from disturbance fields obtained by second and third order curve fitting (a) and vertical wavelength deviation (b) in different interval ranges in the lower stratosphere above Taiyuan during 2014—2017
2阶、3阶曲线拟合扰动场的周期在不同区间内的占有率沿横坐标轴方向的变化较小(图10a),其最大值分别位于 [6,9)和 [3,6),分别为 22.19%和23.84%,次大值均位于(0,3),分别为21.09%和23.45%,而最小值分别位于 [9,12)和 [12,+∞),分别为16.84%和14.48%;3阶与2阶曲线拟合扰动场之间的周期偏差,在不同区间内的占有率(图10b)沿横坐标轴方向呈现出增大、减小变化特征,最大值位于 [0,3)(34.30%),次大值占有率位于 [−3,0)(32.97%),而在(−∞,−12 ]和 [12,+∞)的占有率均较小,合计为1.02%。
4.5 固有相速
2阶、3阶曲线拟合扰动场的固有相速及固有相速相关系数的年内变化(图11)表明,1—12月,2阶与3阶曲线拟合扰动场的固有相速年内变化趋势存在一定差异,且2阶曲线拟合扰动场的固有相速值均大于对应的3阶曲线拟合扰动场(图11a)。1—3月,2阶曲线拟合扰动场的固有相速表现为增大、减小变化特征,而3阶曲线拟合扰动场的固有相速为一致减小;9—12月,2阶曲线拟合扰动场的固有相速表现为减小、增大变化特征,3阶曲线拟合扰动场的固有相速为一致增大变化特征;1—12月,2阶曲线拟合扰动场的固有相速为10.72(1 月)—12.45 m/s(8 月),平均为 11.67 m/s,3 阶曲线拟合扰动场的固有相速为9.00(5月)—10.05 m/s(8月),平均为 9.65 m/s;2阶与 3阶曲线拟合扰动场之间的固有相速相关系数(图11b)1—12月变化为 0.38(6月)—0.75(1月),平均为 0.58。
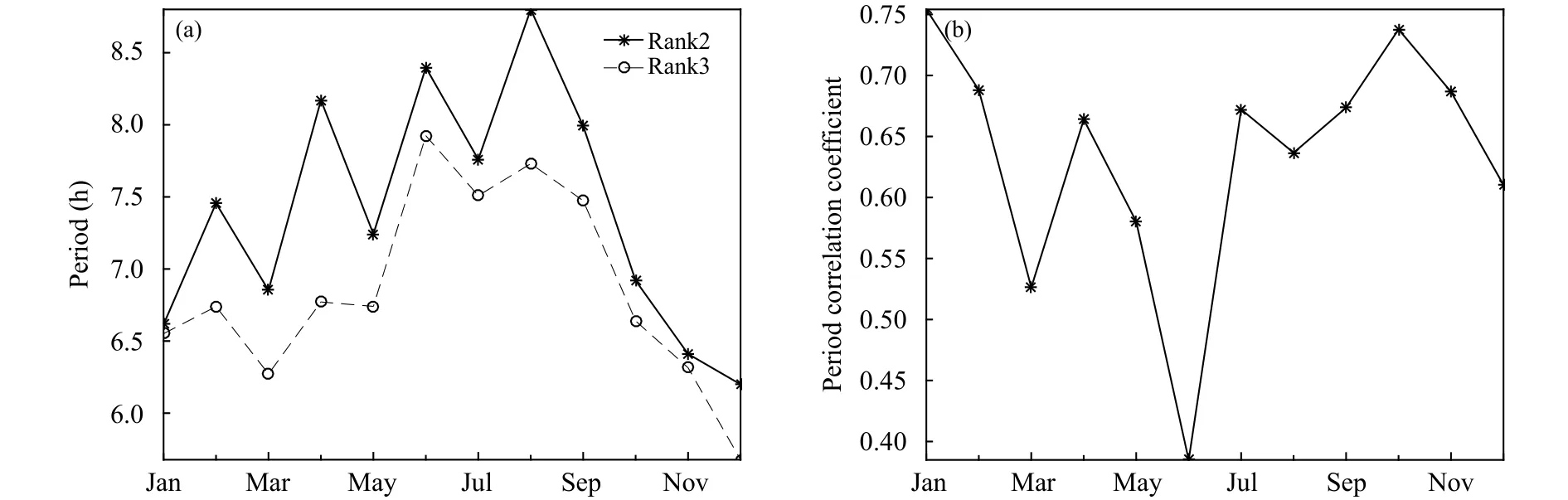
图9 2014—2017 年太原地区下平流层 3 阶与 2 阶曲线拟合扰动场的周期 (a) 和周期相关系数 (b) 的月变化Fig.9 Annual variations of period from disturbance fields obtained by second and third order curve fitting (a) and period correlation coefficient (b) in the lower stratosphere above Taiyuan during 2014—2017
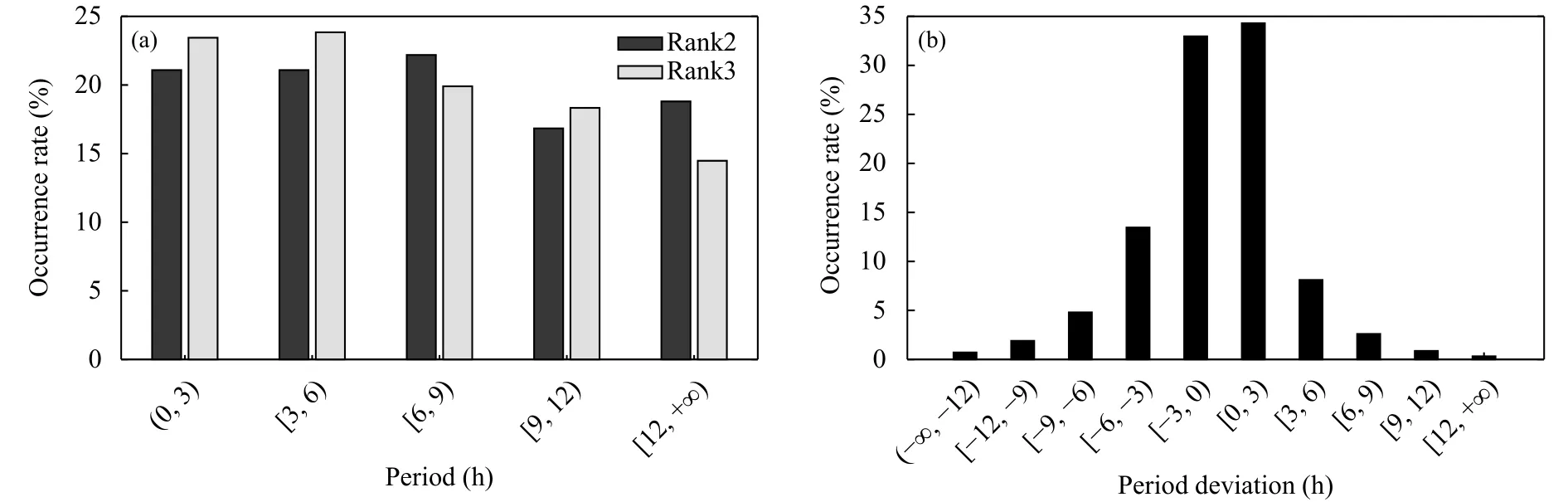
图10 2014—2017 年太原地区下平流层 3 阶与 2 阶曲线拟合扰动场的周期 (a) 和周期偏差 (b) 在不同区间占有率的分布Fig.10 Occupancy distribution characteristics of period from disturbance fields obtained by second and third order curve fitting (a) and period deviation (b) in different interval ranges in the lower stratosphere above Taiyuan during 2014—2017
2阶与3阶曲线拟合扰动场的固有相速在不同区间内的占有率沿横坐标轴方向的变化趋势特征存在差异,2阶曲线拟合扰动场的固有相速呈现一致增大趋势,而3阶曲线拟合扰动场的固有相速表现为增大、减小变化特征(图12a)。2阶、3阶曲线拟合扰动场的固有相速占有率最大值分别位于[12,+∞)和 [8,10),分别为 38.71%和30.45%;次大值分别位于 [10,12)和 [6,8),分别为 23.76%和24.86%;2阶、3阶曲线拟合扰动场的固有相速在(0,2)的占有率均为0.00%,2阶曲线拟合扰动场的固有相速在[2,4)的占有率为0,而相应的3阶曲线拟合扰动场的固有相速占有率为0.08%。固有相速偏差在不同区间内的占有率(图12b)沿横坐标轴方向呈现出增大、减小变化特征,最大值位于 [−2,0)(41.31%),次大值位于 [−4,−2)(20.61%),固有相速偏差在 [2,+∞)的占有率较小,合计为2.99%。
4.6 能量上传率
2阶与3阶曲线拟合扰动场的能量上传率(FWUPE,fraction of wave upward propagation energy)的年内变化趋势基本一致,且两者的数值比较接近(图13a),1—12月,2阶曲线拟合扰动场的能量上传率为 63.79(12月)—75.92%(8月),平均为70.01%;3阶曲线拟合扰动场的能量上传率为65.37(12月)—74.80%(8月),平均为 70.44%。2阶与3阶曲线拟合扰动场的能量上传率相关系数(图13b)1—12月为 0.78(6月)—0.89(5月),平均为0.85。
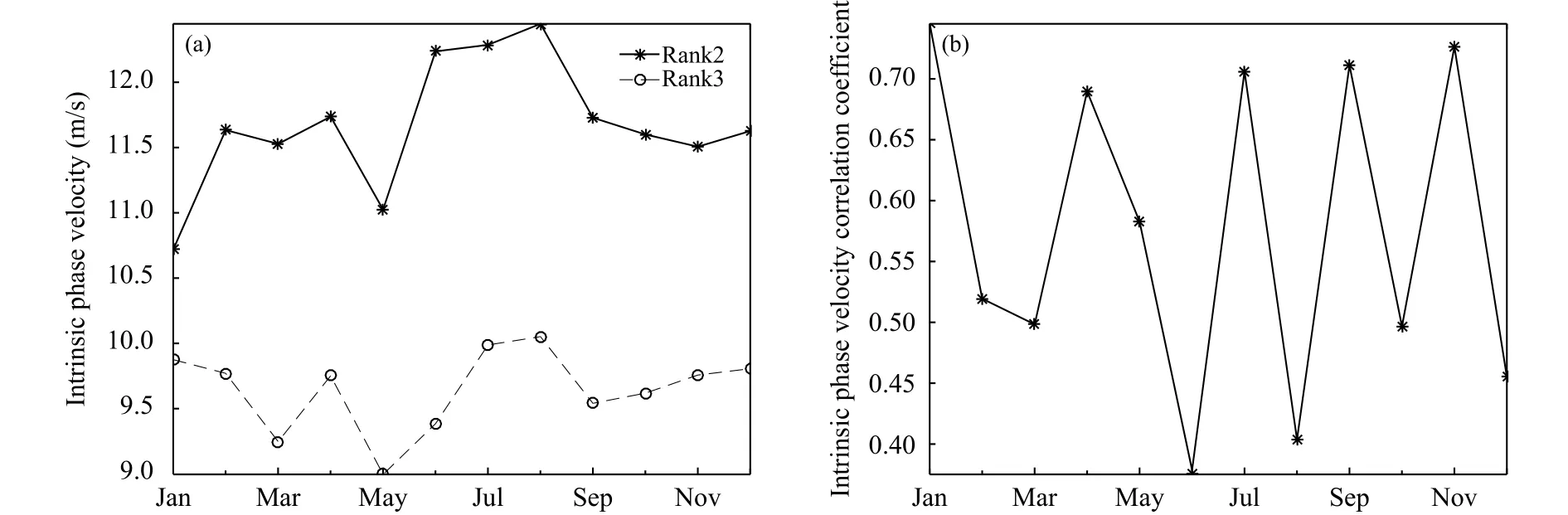
图11 2014—2017 年太原地区下平流层 3 阶与 2 阶曲线拟合扰动场的固有相速 (a) 和固有相速相关系数 (b) 的月变化Fig.11 Annual variations of intrinsic phase velocity from disturbance fields obtained by second and third order curve fitting (a) and intrinsic phase velocity correlation coefficient (b) in the lower stratosphere above Taiyuan during 2014—2017

图12 2014—2017 年太原地区下平流层 3 阶与 2 阶曲线拟合扰动场的固有相速 (a) 和固有相速偏差 (b) 在不同区间占有率的分布Fig.12 Occupancy distribution characteristics of intrinsic phase velocity from disturbance fields obtained by second and third order curve fitting (a) and intrinsic phase velocity deviation (b) in different interval ranges in the lower stratosphereabove Taiyuan during 2014—2017
2阶与3阶曲线拟合扰动场的能量上传率及其之间的能量上传率偏差在不同区间内的占有率分布特征(图14)表明,2阶与3阶曲线拟合扰动场之间的能量上传率的占有率在各区间内基本相同,且均沿横坐标轴方向呈现出增大特征(图14a),最大值均位于 [80,100],分别为39.02%和39.81%,最小值均位于 [0,20),分别为1.65%和1.57%;能量上传率偏差在不同区间内的占有率沿横坐标轴方向呈现出增大、减小变化(图14b),最大值位于 [0,10)(36.66%),次大值位于 [−10,0)(32.02%),能量上传率偏差在(−∞,−50)的占有率为 0.00%,在 [−50,−40)和 [40,+∞)的占有率分别为0.08%和0.24%。
5 结论和讨论
大气重力波在大气中普遍存在,其对全球大气的动力、热力等变化具有重要影响,且与多种不同尺度的天气现象密切相关,为提高大气模式对多种不同尺度天气现象的预报能力,需通过重力波参数化方案引入重力波的影响;目前,确定重力波参数气候特征是研制大气模式中重力波参数化的一个重要前提条件,这些参数的选取需要根据观测资料来确定。中外常采用2—4阶曲线拟合方法扰动场来计算得到大气重力波参数,并以此结果分析大气重力波的气候统计特征,但较少针对不同阶曲线拟合方法扰动场对重力波参数气候特征的影响研究;本文对2—4阶曲线拟合方法扰动场进行对比,统计发现2阶与3阶曲线拟合方法扰动场的相似程度更高;因此,选取相似程度更高的2阶、3阶曲线拟合方法扰动场分别获取大气重力波参数,并对大气重力波参数之间的气候差异特征进行分析,得到如下初步结论:
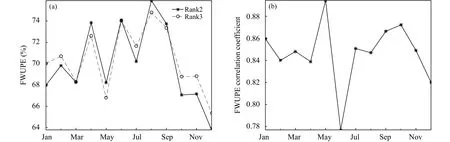
图13 2014—2017 年太原地区下平流层 3 阶与 2 阶曲线拟合扰动场的能量上传率 (a) 和能量上传率相关系数 (b) 的月变化Fig.13 Annual variations of FWUPE from disturbance fields obtained by second and third order curve fitting (a) and FWUPE correlation coefficient (b) in the lower stratosphere above Taiyuan during 2014—2017
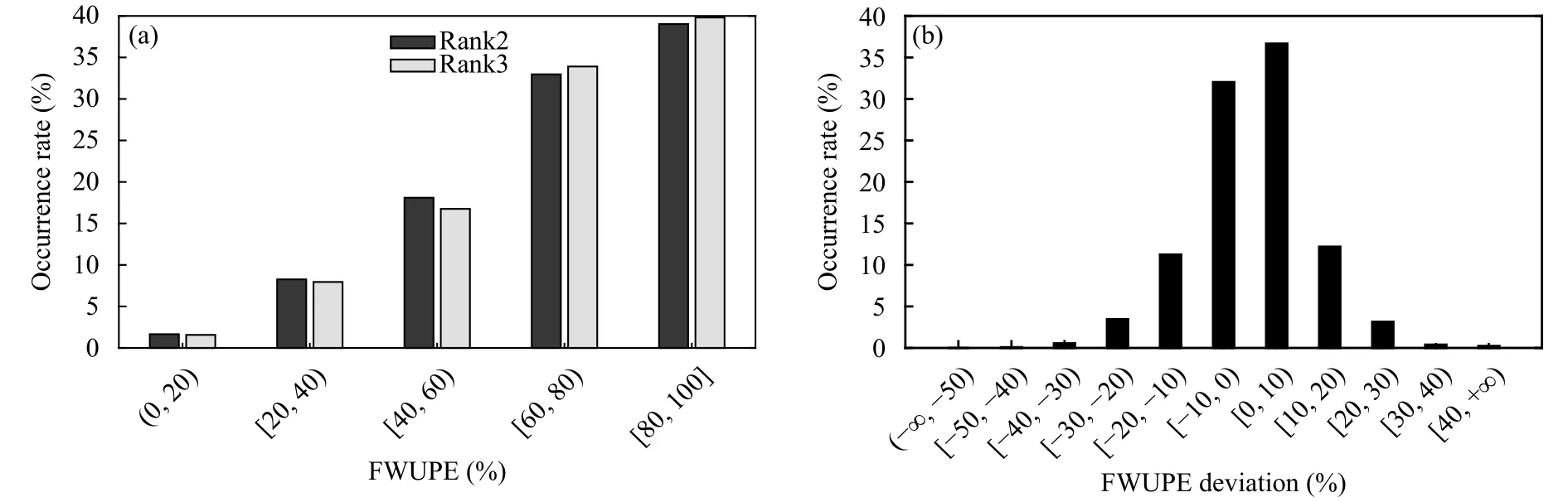
图14 2014—2017 年太原地区下平流层 3 阶与 2 阶曲线拟合扰动场的能量上传率 (a) 和能量上传率偏差 (b) 在不同区间的占有率Fig.14 Occupancy distribution characteristics of FWUPE from disturbance fields obtained by second and third order curve fitting (a) and FWUPE deviation (b) in different interval ranges in the lower stratosphericabove Taiyuan during 2014—2017
(1)基于2—4阶曲线拟合方法,得到高垂直分辨率探空资料纬向风扰动场、经向风扰动场及温度扰动场的值变化范围及随高度变化趋势均存在较明显差异。
(2)3阶、4阶曲线拟合与2阶曲线拟合方法扰动场之间的相关性存在较明显差异;其中纬向风扰动场相关系数值大于0.8的占有率分别为62.54%和27.38%,相应的经向风扰动场分别为45.46%和17.77%,相应的温度扰动场分别为67.54%和40.08%。
(3)不同阶曲线拟合方法扰动场对大气重力波参数大小、变化趋势均具有重大影响;相对3阶曲线拟合方法扰动场,除能量上传率外,基于2阶曲线拟合方法扰动场获取的大气重力波参数均偏大(表2)。
(4)3阶与2阶曲线拟合方法扰动场,获取的不同重力波参数之间相关性存在较明显差异;相关性最强为能量上传率(0.85),最弱为水平波长(0.55)(表2)。
(5)3阶与2阶曲线拟合方法扰动场计算得到的重力波参数及其偏差,在不同区间内的占有率存在较明显差异;其占有率最大值及对应区间见表3。
目前,已有研究成果尚未证实哪阶曲线拟合扰动场获取的重力波参数气候特征与实况更接近,并且针对不同阶曲线拟合扰动场对重力波参数气候特征影响的研究较少,Dutta等(2017)利用2012年4月30日—5月4日(时间分辨率6 h)共20次高垂直分辨率探空资料,同样发现不同阶曲线拟合得到的扰动场廓线存在差异,但没给出相应的重力波参数平均值、年内变化趋势以及重力波参数在不同区间内占有率的差异特征;与此同时,一方面,重力波参数气候特征是确定大气模式中重力波参数化方案的基础数据,通过该基础数据有利于研制更合适的重力波参数化方案,从而进一步提高大气模式对多种不同尺度天气现象的预报能力;另一方面,本研究发现,虽然2阶与3阶曲线拟合方法扰动场的相似程度较高,但基于它们扰动场得到大气重力波参数的数值及变化趋势均存在较明显差异;考虑到目前中外常采用不同阶曲线拟合方法扰动场获取大气重力波参数气候特征,且较少关注不同阶曲线拟合方法扰动场对其气候特征的影响,虽然本文对不同阶曲线拟合扰动场对重力波参数气候特征影响进行了对比研究,并发现它们之间存在较明显差异,如何确定几阶曲线拟合扰动场得到的重力波参数气候特征更接近实况,需要考虑以各阶曲线拟合方法扰动场得到的重力波参数气候特征为试验方案,研制大气模式重力波参数化方案,随后对多种不同尺度天气系统进行数值模拟,最后,选取总体上模拟准确率最高的大气模式重力波参数化方案为最佳方案。

表2 基于2阶、3阶曲线拟合扰动场计算得到的重力波参数平均值及其之间的相关系数Table 2 The average gravity wave parameters and their correlation coefficients based on the second-order and third-order curve fitting disturbance field
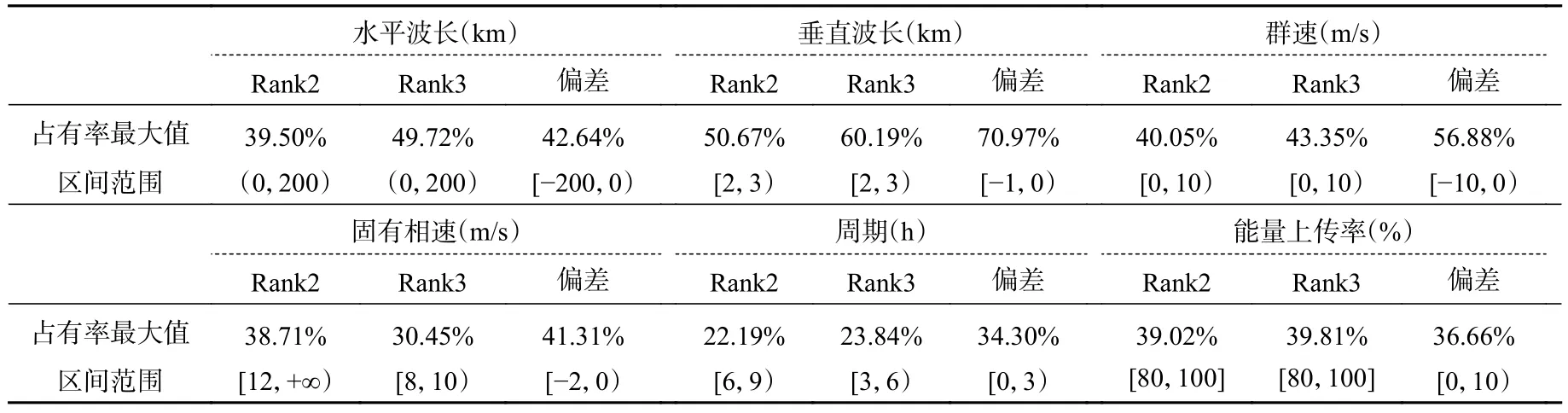
表3 在不同区间范围内,3阶、2阶曲线拟合扰动场计算得到重力波参数值和偏差值的占有率最大值及对应的区间Table 3 In different intervals,The maximum occupancy rate of gravity wave parameter values and deviation values,and the corresponding interval range obtained obtained by the second-order and third-order curves fitted disturbance fields

