面向操作可靠性提升的复合工业机器人运动规划*
裴艳虎 刘志峰 许静静 杨聪彬 郑继贵
(①北京工业大学先进制造与智能技术研究所,北京 100124;② 吉林大学数控装备可靠性教育部重点实验室,吉林 长春 130015;③ 北京工业大学先进制造技术北京市重点实验室,北京100124;④ 北京精密机电控制设备研究所,北京100076)
目前,工业领域开放作业环境给机器人工作空间和灵活性提出了更高的要求,因此,移动装置与机械臂结合形成的复合工业机器人系统得到了初步发展,如图1所示,其工业应用成为实现开放环境下全自动化和智能化制造过程的重要路径[1]。在该类应用中,当机器人面临复杂的作业环境或有限操作空间时,不合理的机械臂站姿会导致其无法避开障碍物到达目标点或无法跟踪目标轨迹,从而导致任务失败,降低系统操作可靠性。然而,当前学者们主要针对移动小车和固定式机械臂分别开展避障运动规划研究。在机械臂避障方面,多数研究旨在基于障碍与目标位姿信息,在关节空间或操作空间内搜索一条无碰撞运动轨迹。形成的方法主要有自由空间法[2]、梯度投影法[3]、人工势场法[4]和其他智能优化算法[5]等。相比而言,针对具有固定特征的复杂作业环境,采用智能优化算法进行离线轨迹优化的方法[6],如图2,能够更有效地保证机器人的综合操作性能。
在避障运动规划中,机器人与操作空间的最短距离是检测碰撞发生及碰撞危险度的关键指标。已有研究主要采用凸多边体[7]、层次包围盒[8]和圆柱体[9]等包络或引入切片理论[10]进行机器人或障碍描述,其中基于切片理论的最小距离建模方法具有运算效率和估算精度高的优点[11]。

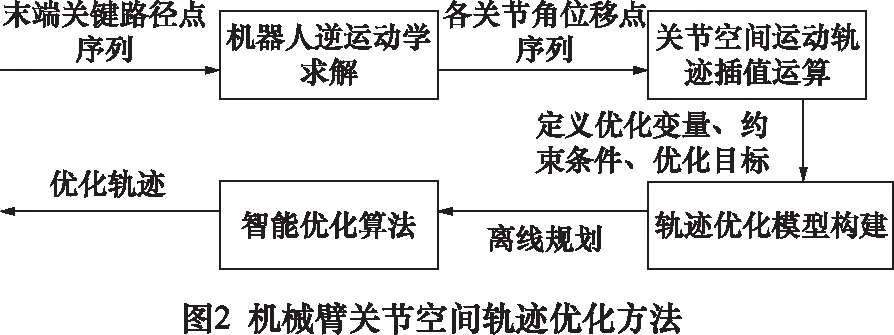
为提升复合工业机器人操作可靠性,文中基于旋量理论建立复合工业机器人运动学模型,采用3阶S型曲线进行插值运算,采用基于切片的避障距离模型[11]构建避障约束条件,同时考虑机器人运动学约束条件,以最小化耗能当量与运动时间为优化目标,构建复合工业机器人运动规划优化模型,并引入粒子群算法(PSO)进行优化求解。最后,通过仿真验证基于优化轨迹的复合工业机器人操作可靠性。
1 复合工业机器人基础建模
基于旋量理论建立复合工业机器人运动学逆解模型是实现关节空间机器人运动规划的关键基础,基于切片方法建立机器人避障距离模型,是构建机器人运动优化避障约束条件的基础模型。
本文针对复合工业机器人,即移动装置、库卡机器人和可轴向转动的执行器集成系统,其中机械臂具有七自由度,如图3。机械臂初始站姿可通过在移动装置运动调整,以其基坐标系为参考,一般包含沿3个坐标轴方向的移动运动和沿z轴方向的旋转运动。即,包括沿x、y和z轴的移动变量δx、δy和δz,及沿z轴的旋转角度β。

1.1 基于旋量的机器人运动学建模基础
本文对应专利(一种基于旋量理论的6R机器人逆运动学几何求解方法)[13]基于经典子问题[14]采用新的逆解子问题及其求解方法,将六自由度串联工业机器人逆解子问题简化为2个多元二次多项式方程组的求解问题,其几何意义更加明确、求解更加简单。
1.2 复合工业机器人运动学建模方法
机器人系统构型及其运动示意如图4所示,复合工业机器人运动被分解为移动平台的运动1和机械臂的运动2。为方便建模,将机械臂原始基坐标系(originalRBF)作为世界坐标系WCS:O-xyz,且机械臂初始站姿调整可反映为基坐标系的位姿调整,调整后的基坐标系记为adjustedRBF。

在实际应用中,操作目标点在世界坐标系下的位姿为Poseo一般通过视觉测量得到,可表示如下:
(1)
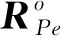
将目标点在WCS下的位姿Poseo转换为adjustedRBF下的位姿。首先,基于移动平台的运动变量X1=(δx,δy,δz,β),由originalRBF到adjustedRBF的转换矩阵可定义为:
(2)
式中:cβ、sβ分别表示角度β的余弦值和正弦值,cβ=cosβ和sβ=sinβ。
基于该转换矩阵,目标点在originalRBF和adjustedRBF下的位姿Poseo和Pose具有关系R·Pose=Poseo。将式(1)~(2)代入该关系式,可得Pose的表达式:

(3)
式中:RPe和Pe分别表示目标点在adjustedRBF下的姿态矩阵与位置向量。
至此,基于移动平台运动后操作目标在机械臂基坐标系下的位姿描述,如公式(3)所示。文中以执行器冗余关节角为变量进行运动规划优化,在逆解问题中,首先假设冗余关节角θR已知,将冗余度机械臂逆解问题转换为六轴机器人逆解问题获取其他关节运动角位移。在前期研究中[13],作者已建立了显式的逆运动学模型,在此处不再赘述。基于专利[13]和式(3)得到的机械臂末端目标位姿,可得到各关节的角位移。
1.3 复合工业机器人避障距离建模方法
文中引入基于切片的避障距离建模方法,具体将具有复杂外形的机械臂结构首先分解为多个连杆结构,具体推导详见文献[11],此处不再赘述。
基于文献[11],整个运动过程中机器人本体与障碍空间的最小距离,可表示为:
Obs=Algorithm[Link,Plane]
(4)
式中:Link表示针对各连杆的所有切片特征点坐标集合,Plane表示所有空间障碍面顶点坐标集合。

(5)
2 复合工业机器人运动规划优化算法
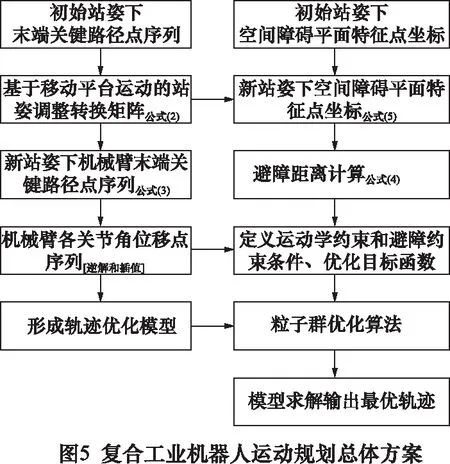
以复合工业机器人运动变量为优化变量,同时考虑运动学约束和避障约束条件,以最小化耗能当量和运动时间为优化目标,建立复合工业机器人运动轨迹优化模型,采用粒子群优化算法进行优化求解。规划优化总体方案见图5所示。文中采用S型曲线进行关节空间插值,然后构建运动规划优化数学模型。
2.1 S型曲线插值方法
S型曲线包括加速、匀速和减速阶段,如图6所示。该曲线的应用可以使机器人各关节角速度在启停时为0,且运动过程中连续,从而能够保证机器人的运动平稳,且无振颤。

基于该曲线特征,各关节角变量可表示如下:
(6)
式中:θs,i、θe,i分别表示机器人第i关节运动的初始和目标关节角度值;Vi、Ai分别为第i关节的最大关节角速度和角加速度,Vi=VratioVmax,i和Ai=AratioAmax,i,其中Vmax,i和Amax,i分别为关节电机结构所允许的最大角速度和角加速度值,Vratio和Aratio分别为角速度与加速度百分比,可在机器人编程中直接赋值;tc为机器人关节运动时间,Ti=2tc+[(θe,i-Aitc2)-θs,i]/Vi。
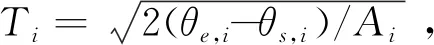
(7)
2.2 运动规划优化模型构建与求解
在轨迹规划时,需要根据环境特征为末端运动选取一个或多个过渡点以保证轨迹优化问题的有解性,设过渡点个数为Ntran,则轨迹被分解为Ntran+1段子运动轨迹。基于以上策略,以最小化运动耗能当量(即用各关节角的绝对变化量之和表征,单位,rad)和运动时间为优化目标,考虑运动学、动力学和避障约束条件,优化问题描述如下,
(8)
式中:Xs为单层优化变量,Xs=(δx,δy,δz,β,θredu,Vratio,Aratio);由于机器人测量目标位姿时,目标一般位于机器人正向位置,因此β取值范围可取为[-π/2,π/2];ω1、ω2表示耗能与时间在优化目标中所占权重,主要为避免两者数量级差对优化结果产生的影响;T表示机器人运动时间,T=max[T1,i+…+TNtran,i|1≤i≤6];Di为第i关节的角变量范围,Di∈[θmin,θmax];i,i,max分别为第i关节的输出扭矩,及为减小机器人启停过程的震颤而给定的扭矩阈值;Tk,i表示第i关节的第k段子轨迹运动时间;δxmin、δxmax,δymin、δymax和δzmin、δzmax分别为移动变量δx、δy、δz的取值上下限,可通过机器人末端到过渡点与目标点的可达性分析进行确定,通过绘制[δx,δy,δz]的点云图,以其可取范围来确定上下限;Tup为机器人总运动时间的上限,根据机器人操作效率需求确定。
针对以上优化问题,本文采用粒子群优化PSO算法进行求解。每次更新迭代时,第m个粒子会根据其现有位置Xm=(xm1,xm2,…,xmD)和飞行速度Vm=(vm1,vm2,…,vmD)得到新的位置,其中D表示变量个数;并结合个体极值pmd和全局极值pgd,通过以下规则更新其速度与位置信息,
vmd=ω×vmd+c1×rand1×(pmd-xmd)+c2×rand2×(pgd-xmd)
(9)
xmd=xmd+vmd
(10)
式中:ω表示惯性权重,其值越大,粒子的全局搜索能力更强,反之局部搜索能力更强,为对比两种算法的优化效率,在优化问题中均取ω=0.01;c1,c2为加速常数,可在区间[1,2]内取值;rand1,rand2为在区间[0,1]内变化的随机值。并根据经验设置群体粒子个数和迭代次数分别为20和50。
3 基于优化仿真的机器人可靠性验证
3.1 运动规划优化仿真
为验证方法可行性,首先进行运动规划优化仿真。该仿真案例中以箱型空间为机器人有限作业空间,各顶点位置见表1。为同时体现避障效果,在该空间内部取一点为操作目标,并设计运动路径如图7所示,其中Ps为机器人末端所在初始点,Petran和Petarg分别为机器人末端的过渡点和目标点,各点的初始位置设置为Petran=[1 300 0 200]和Petarg=[2 100 0 450]。

表1 箱型空间各障碍平面顶点坐标
基于过渡点与目标点的位姿信息,对机器人末端可达性进行分析,绘制确定变量[δx,δy,δz]的点云图,如图8所示。基于点云图可初步确定3个变量的取值范围分别为δx∈[600,3 000],δy∈[-1 400,1 800]和δz∈[-400,1 600],单位为mm。此外,根据机器人的初始位姿,依据经验将3个范围分别缩小至δx∈[600,1 300],δy∈[-300,300]和δz∈[-400,400]。在优化中,机器人关节扭矩阈值取10 Ν·m。

软件Isight是一种集成多个仿真计算软件,可调用多种优化算法(粒子群算法、遗传算法等)的优化分析平台。通过Isight集成Matlab计算软件,并选用PSO算法解决所提出的轨迹优化问题,运算环境见表2。

表2 运算环境
表3为运动规划优化结果。结果表明,在初始姿态的调整下,基于优化轨迹的机械臂运动过程中最小避障距离为11.848 7 mm,说明机械臂与障碍面没有发生接触,可以安全到达目标位姿。

表3 优化结果
3.2 复合工业机器人操作可靠性测试
为验证复合工业机器人针对初始状态变化的操作可靠性,研究通过改变机器人与操作目标的相对位姿,选择了15种初始状态,分别进行运动规划优化仿真,图9为在15种状态下优化轨迹的最小避障距离,均明显大于安全阈值10 mm。


结果表明,应对初始状态改变,机械臂能够100%无碰撞地到达目标位姿,即基于规划优化的复合工业机器人操作可靠性较高。而现有应用中,基于人工经验的机器人初始站姿调整,难以准确把握机械臂的操作可行性和效果。因此,该方法可为复合工业机器人实现工位柔性转换提供可靠的方法支撑。
4 结语
(1)本文基于前期基础,针对复合工业机器人运动特点,提出了基于旋量的运动学逆解方法和基于切片描述的机器人避障距离建模方法,为进行复合工业机器人运动规划优化提供了模型基础。
(2)为提升有限空间内的机器人操作可靠性,建立了一种复合工业机器人运动规划优化模型。该模型通过以移动装置和机械臂运动变量为优化变量,并同时考虑了运动学约束和避障约束条件,得到了最优作业站姿下的机械臂规划轨迹,实现了机器人无碰撞运动过程。
(3)文中采用粒子群优化算法,并借助Isight软件进行的运动规划优化仿真,验证了方法的可行性;进行了15种不同初始状态的仿真实验,结果表明,针对状态变化机械臂能100%无碰撞地到达目标位姿,且最小避障距离均明显高于给定的安全阈值,即基于规划优化的复合工业机器人操作可靠性较高。

