船模波浪载荷试验不确定度分析方法研究
司海龙,顾学康,胡嘉骏,田 超,倪 阳
(中国船舶科学研究中心,江苏无锡 214082)
0 引 言
船模波浪载荷试验是一个复杂的系统工程,整个试验过程包括船模设计、加工、标定、重心和惯量的调整,以及正式试验和数据后期处理等多个环节。影响试验结果的因素非常多且复杂,为了确保试验结果的可靠性,需对船模波浪载荷试验进行不确定度分析。
随着船模试验技术的发展与提高,船舶力学领域的试验不确定度越来越引起人们的重视。根据ITTC 的建议,国内外的研究人员对船模拖曳阻力试验不确定度[1-2]开展过大量的研究。马向能[3]和Irvine[4]分别将不确定度分析方法应用到了船模操纵性试验和耐波性试验当中。Qiu[5]根据不确定度扩展定律对船舶并行作业模型试验的不确定度开展了研究,将不确定度的来源分为流体的物理特性、试验初始状态、模型设计加工及安装、波浪、测量仪器及设备、尺度效应和人为因素等七部分,列出了具体的不确定度来源。采用重复性试验确定A类不确定度,通过标定来确定传感器的不确定度,通过仪器说明书确定测量仪器及设备的不确定度,通过数值模拟来确定模型的几何尺寸、质量分布及锚链安装引起的不确定度。研究发现,几何尺寸引起的不确定度可以忽略不计,但质量分布会对试验结果特别是船体横摇产生较大的不确定度,试验应该特别注意两条船之间的间隙,因为这会对共振频率产生较大的不确定度。可能由于池壁效应或波浪反射的影响,持续时间越长,不确定度越大,B 类不确定度一般大于A类不确定度。Qiu[6]根据不确定度扩展定律,对一艘半潜式平台模型试验的垂荡RAO、锚链拉力以及气隙高度等进行了A 类和B 类不确定度分析,指出模型试验不确定度的来源包含模型线型、模型标定、波浪标定、运动测量系统、锚链、尺度效应、模型的初始位置和浪向角,B 类不确定度高于A类不确定度。
近年来,有关船模波浪载荷试验的不确定度分析与研究也得到了初步的发展。Zhu[7]通过将波浪载荷低频信号有效段分成若干段,基于每段样本的标准差与样本均值的比值研究船体运动与载荷的随机误差。对拖车速度及浪向角引起的不确定度并没有详细分析,只是默认这些因素引起的不确定度较小可忽略不计,高频振动弯矩对波浪遭遇周期的敏感程度远高于低频弯矩[8]。在对13 000 TEU集装箱船波浪载荷开展试验研究时,Zhu[9]发现不规则波中目标波浪谱与实际波浪谱的差异是试验不确定度的一个重要来源,斜浪中,浪向角和航速也是试验不确定度的重要来源。汪雪良[10]就兴波载荷和池壁效应两方面分析了大型LNG船模波激振动试验的不确定度。在对双体船波浪载荷开展模型试验时,汪雪良[11]分析了不确定度主要来源于测试系统和弯矩标定两个方面,并列出了模型试验的误差来源。
不确定度扩展定律是开展试验不确定度研究的理论基础,由于船模波浪载荷试验的复杂性,影响试验结果的因素非常多,且有些因素的影响因子不能直接确定,基于不确定度扩展定律开展船模波浪载荷试验不确定度分析的文献还比较少。本文选取对试验结果可能有较大影响的因素,基于不确定度扩展定律,探索性地建立了一套船模波浪载荷试验不确定度分析方法。
1 不确定度扩展定律
1.1 不确定度扩展定律
对试验进行不确定度评估,测量结果总误差由两种成分组成:精度误差(随机的)和偏差(系统的)。可采用多次测量的方法确定精度误差所引起的不确定度,基于不确定度扩展定律确定偏差引起的不确定度。
令被测量Y是X1,X2,…,XN的函数,则

对方程两边同求方差,则

式中,u(Xi)为变量Xi的标准不确定度,∂f/∂x为影响因子。
则扩展不确定度为

式中,k为变量Y的包含因子。
1.2 确定扩展不确定度

式中,p为置信水平。那么,均值xˉ的扩展不确定度为

式中,ν=N- 1为变量X的自由度。

1.3 波浪载荷的扩展不确定度
对船模波浪载荷开展不确定度分析时,试图将所有影响因素均考虑在内是不现实的,可选取对试验结果可能有较大影响的因素,包括船体线型、转动惯量、重心高、测量梁标定系数、测量仪器、应变片、船体航速、波高等。其中,船体线型、转动惯量、重心高、测量梁标定系数可采用A 类不确定度分析,测量仪器、应变片、船体航速等因素可采用B 类不确定度分析,波高需同时采用A 类和B 类不确定度进行分析。
对于船体波浪弯矩,有

式中,M为船体垂向弯矩,S为船体线型,η为标定系数,J为转动惯量,Cg为重心高,V为船体航速,H为波高,SG为应变片,D为测量仪器。则

根据不确定度扩展定律,弯矩M的偏差不确定度可由式(14)确定:

则弯矩M的扩展不确定度为

式中,k=tp(ν),ν为弯矩M的自由度,

对于S、η、J、Cg等变量,可采用A 类评定对其标准不确定度进行评定,νi=Ni- 1 为各变量的自由度。其中标定系数与波浪弯矩成线性关系,标定系数对波浪弯矩的影响因子即为船体测量梁应变信号;船体线型、转动惯量、重心高度、航速对波浪弯矩的影响因子无法直接得到,可通过数值计算的方法获得;在小波高情况下,可认为波高与垂向弯矩成线性关系,垂向弯矩除以波高即得波高对垂向弯矩的影响因子。
对于应变片、测量仪器等,需要采用B 类评定的方法对其标准不确定度进行评估。采用B 类评定,可通过制造说明书、校准证书、使用手册等提供的有关不确定度参数来进行评定。常用的B 类评定包含以下几种方法:
(1)倍数
如xj取自制造说明书、校准证书、手册,且给出的不确定度U(xj)为标准差的kj倍,则标准不确定度u(xj)=U(xj)/kj。
(2)正态分布
当xj受到多个(至少3个以上)、独立、数量大小差不多的因素影响时,可使其服从正态分布。如给出的不确定度U(xj)对应的置信水准为0.90、0.95、0.99 和0.997,则将U(xj)除以1.64、1.92、2.58 和3 即可得到标准不确定度[12]。
(3)均匀分布
当Xj在[xj-a,xj+a]区间内各处出现的机会相等而在区间外不出现,则Xj服从均匀分布,xj的标准不确定度u(xj)=a/ 3[12]。
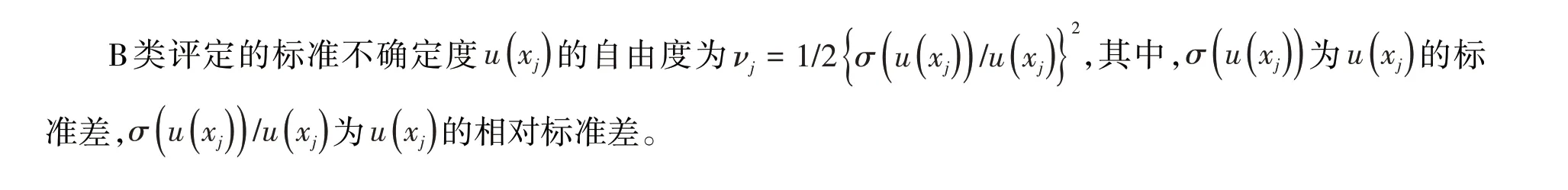
2 船模波浪载荷试验
在中国船舶科学研究中心拖曳水池对某超大型集装箱船波浪载荷开展了模型试验研究。图1为分段的船体模型,表1 为船模的主要参数,船体外壳共分为10 段,分别在2、4、6、8、10+70 mm、12、14、16、18站处切开,各分段通过两根钢质圆管梁装配在一起,船壳切开位置的测量梁上粘贴有应变片,测量不同波高、航速、波长条件下船模波浪载荷。该试验采用拖航的方式。本文主要对该试验的不确定度开展研究。

图1 分段的船体模型Fig.1 Containership model
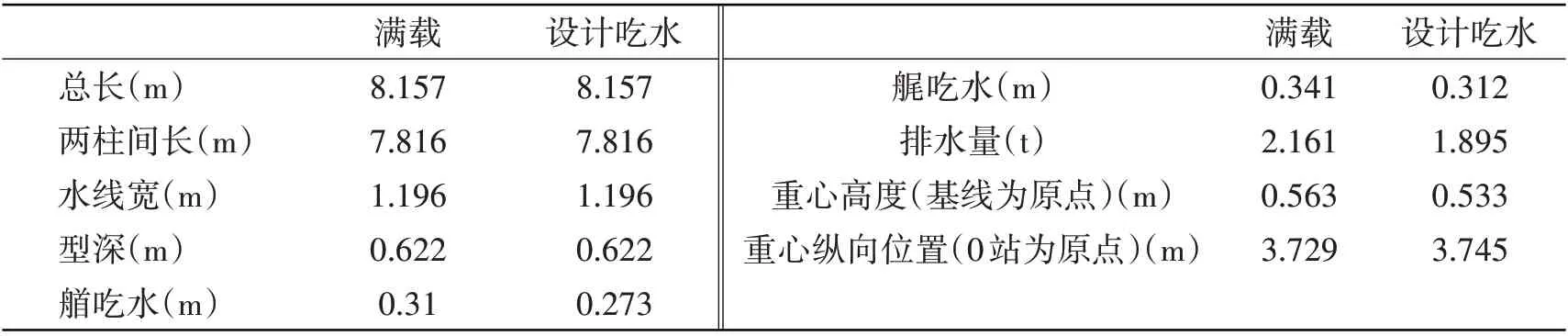
表1 船模主要参数Tab.1 Principal parameters of ship model
3 波浪载荷不确定度
为了对试验的不确定度开展研究,研究人员选取了若干工况进行了重复性试验。本文从中选取一个典型工况,对该工况的试验结果进行不确定度分析。选取的典型工况为满载状态,波高102 mm,波长7.828 m,航速1.69 m/s,顶浪航行。
3.1 精度不确定度
对于典型工况的每次试验,选取有效段,保证有效段内有效子样数大于15个,提取每个周期内的全幅值,并求均值作为该次试验的试验结果。对每次试验结果求均值,进而得到垂向弯矩的标准不确定度。船中垂向弯矩各次试验结果及标准不确定度如表2所示。重复性试验的影响因子为1。

表2 不同工况下船中垂向弯矩Tab.2 Vertical moment of midship in different conditions
在对船体模型的惯量进行调整时,各段的质量重心需满足式(17),其中Mi为各分段重量,包括配重的重量、船壳重量和测量梁质量,xi为各分段重量重心纵向位置,CG为整个船模重心纵向位置,J为船模绕其重心纵向转动惯量,Xi和Xi-1为各分段两端纵向位置。满足该方程的xi有无数种组合,当船模惯量调整并满足要求之后,此时的质量分布只是无数种组合中的一种,质量分布具有一定的随机性,对试验结果也会引入一定的不确定度。为了研究质量分布随机性引入的不确定度,本文在满足重心位置和转动惯量不变的前提下,随机地生成7 种质量分布,基于Sesam 计算各质量分布条件下船中垂向弯矩。在Sesam 水动力计算模型中,每个分段两个质量点。图2 为每种工况的质量分布,表3 为各工况船中垂向弯矩。

图2 质量分布Fig.2 Mass distribution
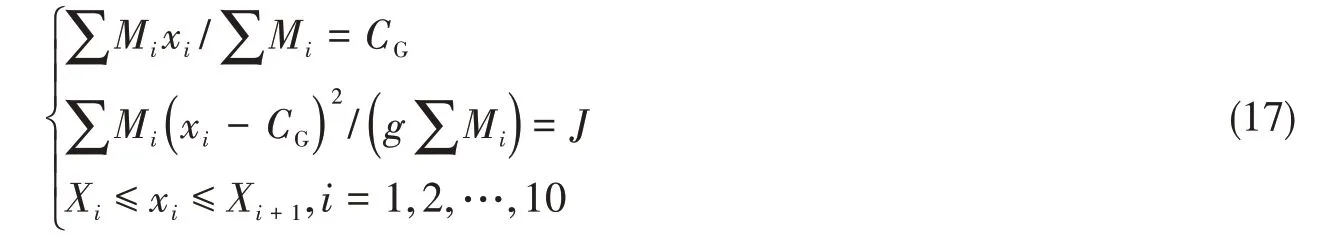

表3 不同质量分布条件下船中垂向弯矩Tab.3 Vertical moment of midship with different mass distributions
3.2 偏差不确定度
引起船体波浪载荷试验偏差不确定度的因素非常多。本文选取可能对试验影响较大的因素进行分析,包括船体线型、转动惯量、重心高度、标定系数、测量仪器、应变片、航速、波高等。
3.2.1 船体线型
该船模的精度指标是线型误差小于0.5 mm。船模加工过程中,研究人员加工标准的钢质卡板,将卡板卡在对应的船体剖面处,用塞尺对船体线型与钢质卡板之间的缝隙进行测量,沿着船体横剖线在船体左右舷侧、底部分别测量船壳与卡板的缝隙的宽度。通过测量发现,对于同一剖面,往往有些位置与卡板贴合得非常紧密,有些位置与卡板之间有缝隙。为简单与方便,选取各剖面缝隙的最大值作为该剖面实际线型与要求线型的误差。各剖面线型误差最大值如表4所示。以各站的最大误差值为一个子样,按照公式(7)计算线型的标准不确定度。

表4 线型误差Tab.4 Offsets of ship’s linetype
为了研究线型误差对波浪载荷的影响因子,本文对船体型线进行了修改,使型线分别向其法向内移或外移0.1 mm、0.2 mm、0.3 mm、0.4 mm 和0.5 mm,基于Sesam 计算不同线型下船中剖面M5 处的垂向弯矩,确定线型对垂向弯矩的影响因子。计算结果如表5 所示,其中“-”表示型线内移,“+”表示型线外移。

表5 不同线型条件下船中垂向弯矩Tab.5 Vertical moment of midship with different linetypes
由图3 和图4 中的计算结果可以看出,对船体原始线型进行轻微改变,船中剖面垂向弯矩随船体型线的改变成线性变化,型线向外偏移,船中波浪载荷增大。对计算结果进行线性拟合,可得拟合公式为
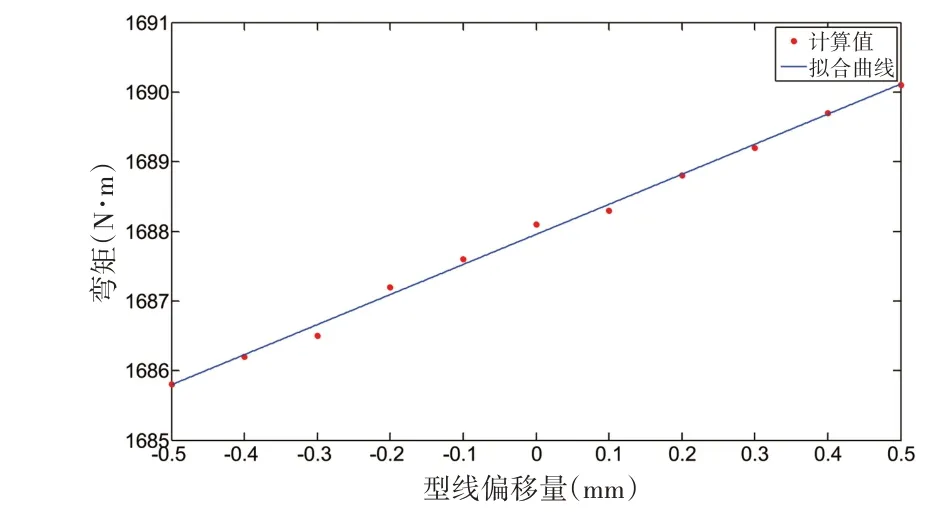
图3 不同线型条件下船中垂向弯矩Fig.3 Vertical moment of midship with different linetypes
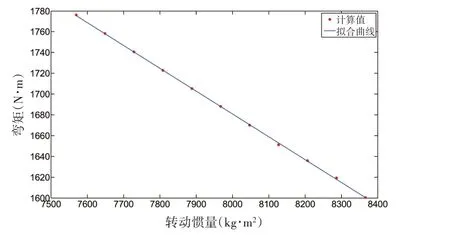
图4 不同转动惯量条件下船中垂向弯矩Fig.4 Vertical moment of midship with different rotational inertia

式中,S为线型改变量,故可得船体线型对船中弯矩的影响因子为4318.2 N。
3.2.2 转动惯量
在试验之前,需对船体绕重心纵向转动惯量与船体重心位置进行调整。在保证每个船体分段的质量满足质量分布的前提下,通过移动配重的纵向或垂向位置,使得船体纵向转动惯量与重心纵向、垂向位置尽量与要求值保持一致。该试验对船体转动惯量进行了8次测量,如表6所示,根据公式(7)计算出纵向惯量的标准不确定度。

表6 转动惯量Tab.6 Rotational inertia of ship model
为了得到船体纵向转动惯量对船体波浪载荷的影响因子,在保证船体重心纵向、垂向位置不变的情况下,通过调节各个分段配重的纵向位置,使船体纵向惯量发生轻微改变,基于Sesam 计算船中剖面M5的垂向弯矩,计算结果如表7所示。研究发现,对船体纵向惯量进行轻微改变,船中垂向弯矩与船体纵向惯量呈线性关系,随着船体纵向惯量的增加逐渐减小。对计算结果进行线性拟合,如图4所示,得到拟合公式为

表7 不同转动惯量条件下船中垂向弯矩Tab.7 Vertical moment of midship with different rotational inertia

式中,J为船模绕重心的纵向转动惯量,故可得船体纵向转动惯量对船中弯矩的影响因子为-0.2198/s2。
3.2.3 重心高度
通过调整配重垂向高度来调整船模重心高度,使得船模重心高度满足试验要求。对重心进行了7次测量,如表8所示,通过公式(7)计算船体重心高的标准不确定度。

表8 重心高度Tab.8 Height of gravity center
为了得到船模重心高度对波浪载荷的影响因子,保证配重纵向位置不变,通过改变配重垂向位置来调节船模重心高度。通过Sesam 计算船中垂向弯矩,计算结果如表9 所示。研究发现,随着船体重心高度的增加,船中剖面弯矩成线性逐渐减小。对其进行线性拟合,如图5 所示,可得拟合公式为

表9 不同重心高度条件下船中垂向弯矩Tab.9 Vertical moments of midship with different gravity center’s heights

图5 不同重心高度条件下船中垂向弯矩Fig.5 Vertical moment of midship with different gravity center’s heights

式中,h为船模重心高度,可得重心高度对弯矩的影响因子为-67.2727 N。
3.2.4 标定系数
通常情况下,测量梁与船体分段模型装配以前,需对船体测量梁进行标定,确定外部载荷与测量梁应变之间的关系,即标定系数,也称应变系数。船模波浪载荷根据船体各剖面在波浪中的信号与标定系数得到,即公式(21)。为了研究标定系数的不确定度,本文研究了不同仪器、不同导线长度、不同标定方式对标定系数的影响。

式中,M(t)为波浪诱导弯矩,δ为标定系数,ε(t)为应变信号。
按照图6中的标定方法,试验人员分别采用Dewesoft和瑞风两种仪器对测量梁进行标定。将测量梁两端简支,载荷施加于距离支点相同位置处,通过逐步加载然后逐步卸载的方法,确定标定系数。标定系数如表10 所示。综合来看,测量仪器引起的误差均小于0.8%。两种仪器测量误差虽小,但为了提高试验的精度,在整个试验过程中,标定阶段与正式试验阶段测量仪器也应尽量保持一致。

图6 船体测量梁标定示意图Fig.6 Calibration of measurement beam
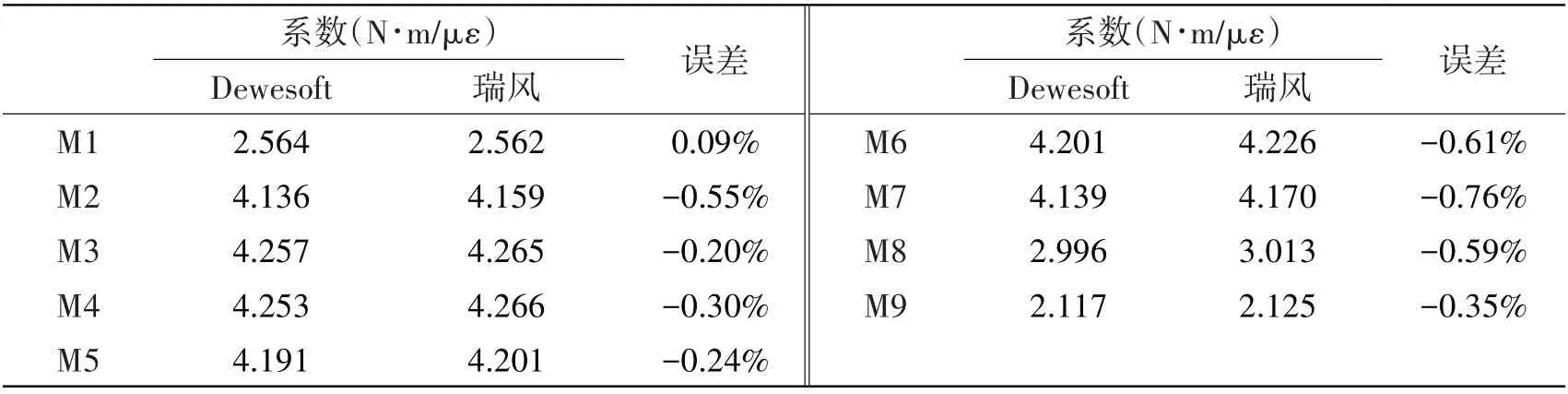
表10 不同测量仪器得到的标定系数Tab.10 Calibration coefficients with different measurement devices
应变片与测量仪器之间通过一定长度的导线连接,导线的长度对标定系数也有一定的影响。按照图6 中的标定方法,对导线在不同长度条件下船中剖面M5 的标定系数进行了研究,标定结果如表11所示。可以发现,相同条件下,导线越长,测量点的应变信号越小,相应的标定系数越大。在试验过程中,应尽量使标定阶段使用的导线长度与正式试验阶段中使用的导线长度相等。

表11 测量导线长度不同时的标定系数Tab.11 Calibration coefficients with different wire lengths
测量梁与船体外壳装配后,通过位于船艏和船艉的吊绳将船模吊起,在船体重心处加载砝码,对标定系数进行了又一次的测量,采集仪器为Dewesoft,导线长度为8 m。如图7 所示,标定系数如表12 所示。由试验结果可发现,除了M1 外,其余各剖面的标定系数均大于单独标定测量梁时的标定系数。二者之间的误差可能来自于测量梁与船体分段进行装配后,测量梁的状态发生了一定的改变。测量梁与船体外壳装配之后,船体状态更符合实际情况,采用装配之后的标定系数更加精确。对标定系数进行了6次测量,标定结果如表13 所示。由公式(21)可知,标定系数的影响因子为随时间变化的应变信号。

图7 装配后标定示意图Fig.7 Calibration after assembly

表12 装配前后各剖面标定系数Tab.12 Calibration coefficients of different sections prior and after assembly

表13 装配后船舯标定系数Tab.13 Calibration coefficients of midship after assembly
由以上对比结果可知,导线长度、仪器、测量梁与船壳的装配都会对标定系数产生一定的影响,为了避免标定方法自身带来的误差,标定阶段与正式试验阶段需要采用相同的测量仪器与导线,同时应采用测量梁与船壳装配后的标定系数。
3.2.5 应变片
该试验在测量梁上下表面各粘贴一枚单向应变片,四个应变片用全桥的形式进行连接,如图8所示,应变信号为四个应变片信号的线性组合,可表达为公式(22)。该试验采用日本共和的型号为KFGS-3-120-C1-11L1M3R的单向应变片,应变片灵敏度系数为2.09±1.0%,电阻为120.4±0.4%Ω。因为该试验是通过试验前的标定系数与波浪中的信号得到波浪载荷,由应变片引起的试验不确定度已包含在标定系数之中。该类型号的热膨胀系数为1.17E-5/°C,开展波浪载荷试验时的温度为23°C,测量梁标定时的温度为32°C,但由公式(22)可知,该方法可消除由于温度变化引起的应变信号变化。
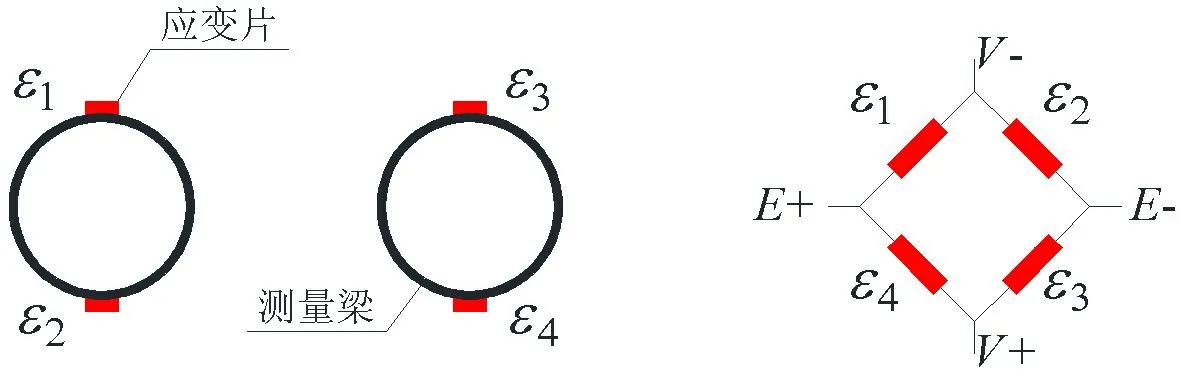
图8 测量梁应变片Fig.8 Strain gauge of measurement beam
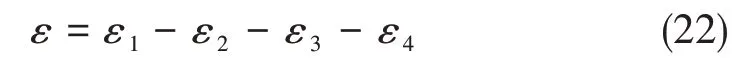
3.2.6 测量仪器

3.2.7 航速

3.2.8 波高

根据4.1节中的弯矩处理方法对典型工况的重复性试验的波浪测量信号进行分析,得到典型工况的波高的精度不确定度,如表14所示。

表14 波高Tab.14 Wave heights
将波高视为单独的被测量,则波高的标准不确定度由测量仪器引起的标准不确定度和波高精度不确定度组成,由公式(12)可得波高的标准不确定度为0.1325 mm,由公式(16)得到波高自由度为10.67。可认为小波高条件下,弯矩与波高成正比,波高对船中垂向弯矩的影响因子为-M/-w=18 241.2 N,其中-M为船中垂向弯矩9次试验的均值,-w为波高9次试验均值。
3.2.9 标准不确定度

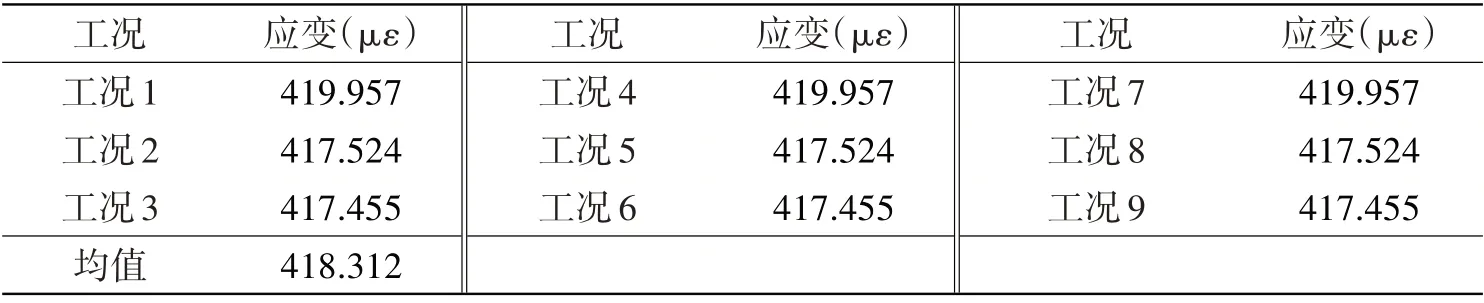
表15 船中应变Tab.15 Strain of midship

表16 标准不确定度Tab.16 Standard uncertainty

续表16
3.3 合成不确定度
根据公式(12)可得垂向弯矩的合成不确定度uc( )M为7.657,根据公式(16)计算得到垂向弯矩的自由度为16.06,可得船中垂向弯矩不同置信水平下的置信区间,如表17所示。

表17 垂向弯矩测量置信度Tab.17 Confidence interval of vertical moment
4 结 论
根据不确定度扩展定律,本文对某超大型集装箱船波浪载荷模型试验进行了不确定度研究,建立了一套完善的波浪载荷模型试验不确定度分析方法,给出了船中垂向弯矩在一定置信水平条件下的置信区间,得出如下结论:
(1)对于船中垂向弯矩,标定系数引起的不确定度最大,其次是转动惯量引起的试验不确定度,精度不确定度与波高引起的偏差不确定度量值相当,但都小于标定系数和转动惯量引起的不确定度,船体线型、重心高度、应变片、测量仪器引起的试验不确定度可忽略不计。
(2)精度不确定度由两部分组成,一部分是试验随机误差,另一部分是船模质量分布的随机性。
(3)测量梁和船壳的装配会对标定系数产生一定的影响,应采用装配之后的标定系数;在标定阶段和正式试验阶段,应尽量使测量仪器和导线保持一致。

