浮力塔平台吸力桩承载力研究

潘徐杰，杜守继，CHEN Weimin，WANG Ge，方智超

（1.上海交通大学船舶海洋与建筑工程学院，上海 200240；2.Wison Offshore Technology Inc.,Houston 77042）

0 引 言

浮力塔平台是由TLP 平台及Spar 平台的发明人Edward E.Horton 与顺应式平台及牵索塔平台的发明人Lyle David Finn 共同提出的一个新的工作平台形式[1]。浮力塔采用类似Spar平台的塔体，与之不同的是，浮力塔通过底部的吸力桩将塔体及上部结构固定在海床上，同时采用顺应式平台的理念随波浪运动，并且凭借重力与浮力组成的力矩回复。浮力塔多年运营已证明了该技术的可靠性[2]。在浮力塔平台中，吸力桩是一个核心环节，它在支持浮力塔主体及上层建筑的同时，也承受着上部传递下来的风、浪、流力，并且吸力桩的约束也改变了浮力塔的运动特征。由此可见，浮力塔吸力桩基础的承载特性极其重要[3]。

吸力桩又被称为吸力沉箱、吸力锚、负压锚或桶形基础等，是一种底部敞开、上端封闭的钢制圆桶结构，也可以做成箱型或其他形状的结构。1994年7月挪威国家石油公司建成的一座新型大型导管架平台Europipe16/11E，成功地采用了吸力桩作为其基础，这也被认为是吸力桩在海洋工程中的首次正式运用[4-7]。随着Europipe16/11E多年的稳定运营，吸力桩的优势逐步被接受，各方面的研究也逐步展开，这些工作包括理论方面的研究[8]、试验方面的研究[9-11]以及数值模拟方面的研究[12-13]，其研究的范围基本上都是聚焦吸力桩的承载力本身。浮力塔的吸力桩不同之处在于：（1）浮力塔是一种顺应式平台，吸力桩的承载特性关系桩基能否安全作业；（2）周围土层对吸力桩的约束将改变浮力塔在波浪中的运动形态与幅度，而运动性能也与平台的安全息息相关；（3）浮力塔的吸力桩处于受压状态，这有别于作为系泊点或导管架平台基础等处于受拉状态的吸力桩。以上三点说明浮力塔的吸力桩有别于目前海洋工程界其他形式吸力桩，到目前为止，关于浮力塔平台吸力桩的承载力研究在文献中尚未提及。

因此，本文针对浮力塔平台吸力桩特征，首先结合平台现场运动的观测结果，分析了土层对吸力桩的约束情况，并确定了吸力桩的分析工况；其次借助数值模拟手段，分析了吸力桩的承载力，并对比了承载的理论结果与平台运动的实际观测值；最后基于承载力分析结果，将土层对吸力桩的约束转换为土弹簧后对平台进行运动分析，并对比了运动分析的结果与平台的实际观测值。

1 土层对浮力塔吸力桩的约束

浮力塔平台是一种近似的对称结构，柱体可采用单柱结构类似于Classic Spar，也可以采用多柱结构类似于Cell Spar。首制浮力塔CX-15 平台选取了四柱柱体结构，如图1 所示。如果没有吸力桩（如图2 所示）的约束，浮力塔将类似于Spar 平台在波浪中绕泥线上柱体中的一点做六自由度运动；当吸力桩周围土层对吸力桩有约束作用时，浮力塔的运动中心将从泥线上柱体中的某一点下移至泥线下的某一点，并且运动的频率、幅度也将发生根本的改变。

图1 首制浮力塔平台CX-15Fig.1 First buoyant tower CX-15

图2 浮力塔CX-15平台的吸力桩Fig.2 Suction caisson of CX-15

与平台在波浪中的运动一样，周围土层对吸力桩的约束可以用6×6的矩阵来表示，如式（1）所示。式中k11、k22、k33、k44、k55和k66分别代表土层对吸力桩的纵荡、横荡、升沉、横摇、纵摇与艏摇的约束，其他项为耦合约束，以k12、k13、k14、k15、k16为例，分别代表纵荡与横荡、纵荡与升沉、纵荡与横摇、纵荡与纵摇、纵荡与艏摇的耦合约束，其他各项以此类推。

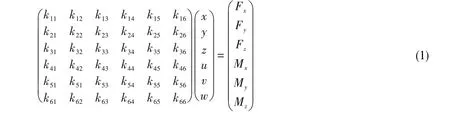
结合平台的实际运动情况，上述36个约束并非全部起作用，并且鉴于浮力塔平台是对称结构（由图1 和图2 所示），所以有部分的约束是相同的。浮力塔在波浪中的运动根据现场实际观测包括横摇与纵摇运动，以及横荡、纵荡、升沉与转动的运动趋势，从而实际起作用的直接约束包括纵荡、横荡、升沉、纵摇、横摇与艏摇的约束。其中纵荡与横荡的约束相同，纵摇与横摇的约束相同，虽然在实际运动中有艏摇的趋势，但鉴于浮力塔在实际工作中未发生转动，且艏摇与其它自由度运动耦合性弱，故将其忽略，需要关注的直接约束为纵/横荡约束k11（=k22）、纵/横摇约束k44（=k55）与升沉约束k33。而在耦合约束中，以横荡与横摇耦合及纵荡与纵摇耦合最为重要，这是因为无论在水平力或者是弯矩的作用下，浮力塔平台的横荡与横摇耦合（或运动趋势）都是相伴发生的，而纵荡与纵摇耦合约束鉴于平台的对称性与横荡及横摇耦合约束相同，所以需要关注的耦合约束为k15（=-k24=-k42=k51）。

2 浮力塔吸力桩基础的承载力

以首制浮力塔平台CX-15 为研究对象，分析吸力桩基础的承载力。在传统的吸力桩承载力分析中，最常见的分析工况包括水平方向的承载力和竖直向上的承载力[11]两个典型工况，其他常见的分析工况诸如斜向上方的拉力等。浮力塔吸力桩的承载力需要结合浮力塔的实际运动情况考虑，根据上述土层对浮力塔吸力桩的约束分析可知，浮力塔吸力桩承载力分析重点包括升沉运动下吸力桩承载力、横荡与横摇（纵荡与纵摇）耦合运动的承载力两个方面。

浮力塔吸力桩在升沉运动下的承载力分析，实质上是吸力桩在竖直向下集中力的作用下发生向下的升沉运动，这有别于传统的吸力桩竖直向上的承载力。在浮力塔的设计中，为了保证由吃水变化所引起的浮力变化不会造成吸力桩的上拔效应，所以在平台底部设有压载舱，并用铁矿砂压载。以CX-15为例，通过压载后保证有3000 kN的重量作用在吸力桩上，即使因落潮导致浮力减少，也要保证吸力桩受到向下的力，即浮力塔吸力桩需要考察竖直向下的承载力。

浮力塔吸力桩在横荡与横摇耦合运动下的承载力分析，实质上是吸力桩在载荷的作用下，发生横荡与横摇的耦合运动。这里的载荷可以是水平集中力，也可以是力矩，如果是水平集中力，则该工况与传统吸力桩的水平承载力分析一致。在本次分析中，横荡与横摇耦合运动下的承载力需要分析在水平集中力单独作用和弯矩单独作用的两个情况，除了考察吸力桩承载力外，还要进一步求得土弹簧对吸力桩的约束刚度。

综上所述，浮力塔吸力桩承载力研究的模拟分析工况应包括：

（1）吸力桩在向下的集中力Fz作用下，考察吸力桩向下的位移情况；

（2）吸力桩在水平集中力Fx作用下，考察吸力桩的水平位移和摇动情况；

（3）吸力桩在弯矩My作用下，考察吸力桩的水平位移和摇动情况。

2.1 本构模型与参数

首制浮力塔平台位于秘鲁西北沿海Corvina CX-15 水域，水深53.4 m，现场地质勘探的土层分布情况如表1所示，首制浮力塔平台的吸力桩在泥线下的插深为8 m，结合实际情况，确定在分析吸力桩基础的承载力时只需要考虑最上面两个土层。

基于有限元软件Abaqus，建立桩土相互作用的半圆柱有限元模型，如图3 所示，吸力桩周围的土层深度选取为31.4 m，分为两个土层。由表1 可知这两个土层均为黏土，并且主要的持力层为软黏土至硬黏土，而根据海床自然固结以及受到浮力塔平台竖直向下压力的实际情况可以判断，土层符合正常固结与弱超固结的特征，从而选取修正剑桥模型为土的本构模型。依据静力触探结果、固结试验以及三轴压缩试验，可以获得剑桥修正模型的参数，如表2所示。按照首制浮力塔平台CX-15 实际情况，吸力桩为桶型结构，直径为8 m，泥线下埋深8 m，吸力桩底部敞开，顶部与浮力塔平台焊接，在实际建模中忽略浮力塔平台。根据现场实际观测，吸力桩强度足够，平台运营多年未发现明显变形，所以模拟中将吸力桩基础假设为刚体。

表2 剑桥修正模型参数Tab.2 Modified Cam-Clay parameters

图3 吸力桩基础有限元模型Fig.3 FEM model of suction caisson

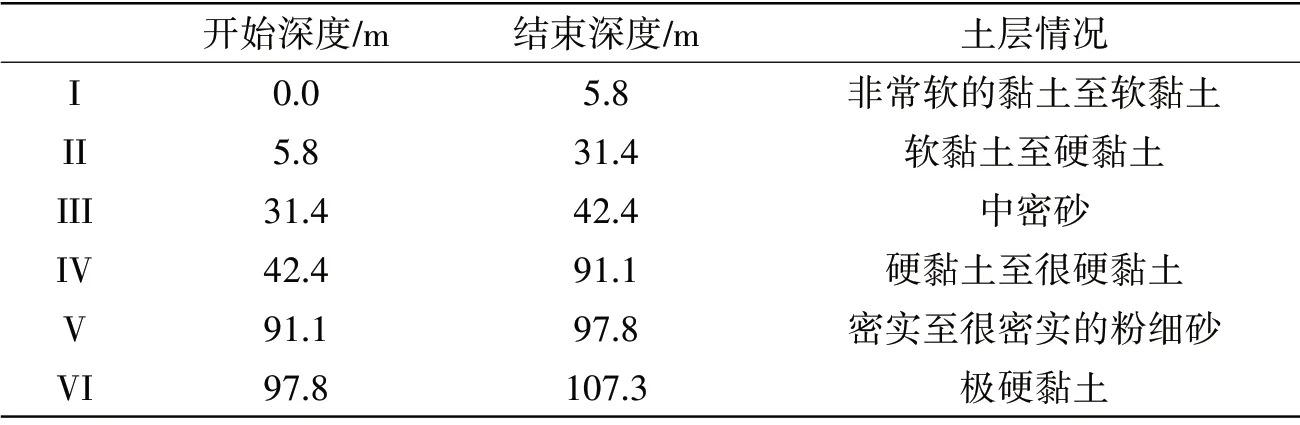
表1 土层分布情况Tab.1 Soil conditions

土层的初始应力、孔隙比、渗透率等根据静力触探结果拟合成函数输入到Abaqus 中作为初始条件。模拟中力的作用点加载于吸力桩顶部的圆心处，在模拟中选取载荷控制法，在模拟中逐步增大施加载荷，监测吸力桩的位移，在模拟中软土变形过大时终止模拟，此时可认为土壤已经完全进入塑性破坏阶段。

2.2 吸力桩在向下的集中力Fz作用下的承载力分析

吸力桩在向下的集中力Fz作用下的承载力分析，从平台的运动角度上看，就是浮力塔在升沉运动下吸力桩的承载力分析，其P-S曲线结果如图4所示。

承载力曲线的分析方法有两种：第一种为直接分析承载力曲线，曲线分为陡变段和缓变段两段。首先是陡变段，在陡变段中位移随着载荷的增大而迅速变大，然后出现拐点，出现缓变段，在缓变段中，载荷基本不发生变化而位移迅速增加，陡变段可以近似地认为吸力桩周围的土层处于弹性阶段而缓变段可以认为吸力桩周围的土层进入塑性破坏阶段；第二种方法为对承载力曲线求一次导数得到土弹簧刚度曲线，当刚度较大时，吸力桩周围土层处于弹性阶段，对吸力桩能够提供足够的回复力，当刚度消失时，吸力桩周围土层处于完全塑性阶段，对吸力桩已不能提供回复力。

图4 列出了吸力桩在向下集中力Fz作用下的承载力结果。从图中可以看出：无论是承载力曲线还是土弹簧刚度曲线，都能清晰地判别出曲线的陡变段和缓变段，但拐点不是特别清晰；但在陡变段和缓变段之间，有一个弧形的过渡段，在这个弧形过渡段中，随着向下集中力Fz逐渐加大，吸力桩周围土层的弹性变化逐渐减小，塑性变化逐渐增加，直至最终周围土层进入塑性破坏阶段。

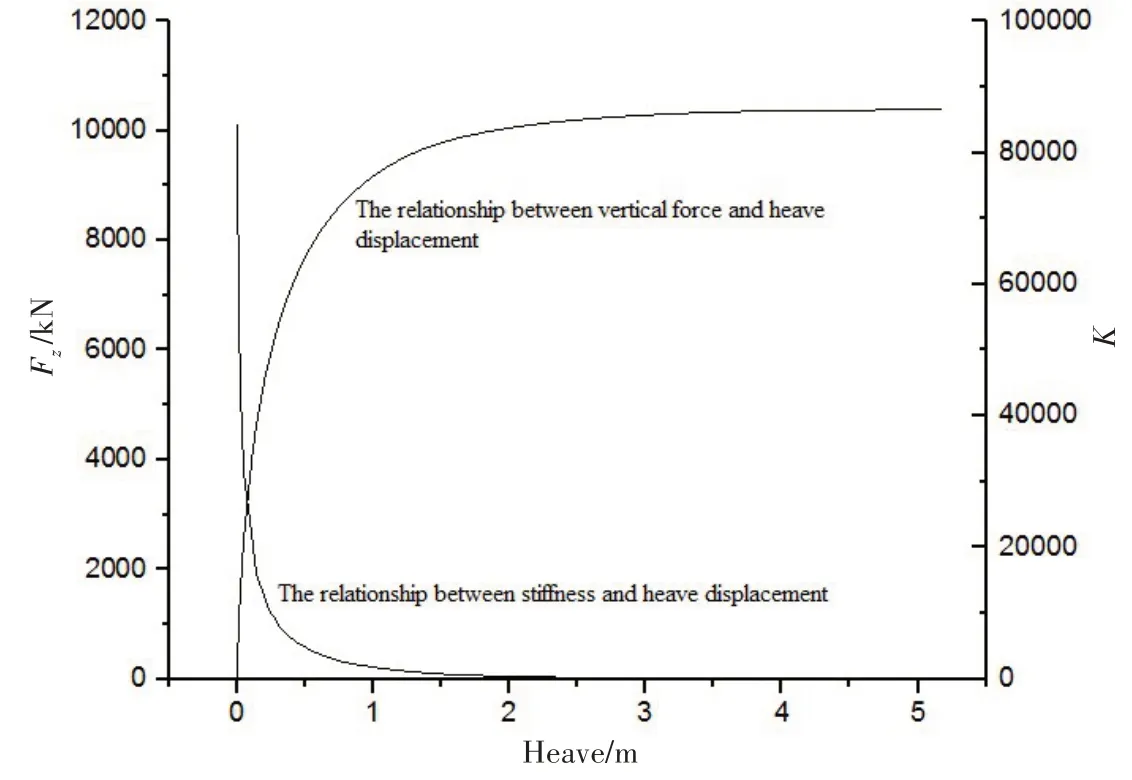
图4 竖向集中力/刚度与升沉位移的关系Fig.4 Relationship between vertical force/stiffness and heave displacement

从图4 中可以看出：深沉运动0.2 m 这个点明显处于承载力的陡变段，即吸力桩的升沉运动在0.2 m 之内，周围的土层明显处于弹性阶段，此时受到的竖向集中力大约为5000 kN，土弹簧的刚度大约为25 000 kN/m；而当吸力桩在受到8000 kN 以上的竖向集中力时，整个桩基才逐步进入过渡段，此时土弹簧的刚度已小于3000 kN/m。在CX-15平台的初始设计中，通过压载使得吸力桩受到3000 kN 的向下压力，而浮力塔在波浪中升沉运动时，会导致吸力桩受到的压力在一定范围内变化。当遇到百年一遇的波谷加低潮位时，吸力桩受到的压力大约在5000 kN。基于上述分析，显然可以看出其仍然在安全的范围内工作，并且3000 kN的初始压力能保证吸力桩在整个运营期间不会受到上拔力。

2.3 吸力桩在水平集中力Fx作用下的承载力分析

吸力桩在水平集中力Fx作用下的承载力分析，从平台的运动角度上看，就是浮力塔在水平力作用下吸力桩横荡与横摇耦合运动的承载力分析。其P-S曲线结果如图5 与图6 所示，其中图5 列出了水平力与横荡的位移关系，而图6列出了水平力与横摇的位移关系。

图5 和图6 保持了高度一致的关系，并且与图4 有着相似的性质，即存在陡变段、过渡段及缓变段。从图中可以看出，大约在受到1750 kN 时，承载力曲线与刚度曲线逐步进入过渡段，也就是说，桩基周围的土层塑性变化逐步增加直至完全进入塑性破坏阶段。1750 kN 对应的桩基横荡位移大约是0.25 m 左右，横摇角度大约为3.5°。虽然在CX-15 平台的实际观测中，无法得知现场的水平力情况，但可以通过实际运动位移来判别桩基安全与否，在实际的位移观测中，平台几乎观测不到横荡运动并且横摇角度也不超过2°，结合承载力曲线及刚度曲线可以判断出，吸力桩在安全的范围内工作。

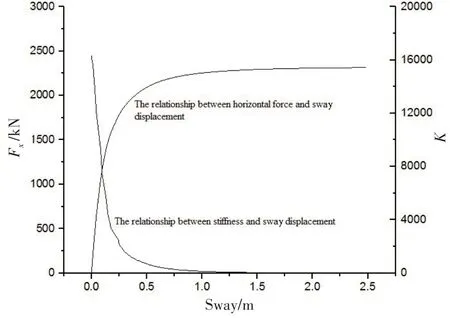
图5 水平集中力/刚度与横荡位移的关系Fig.5 Relationship between horizontal force/stiffness and sway displacement

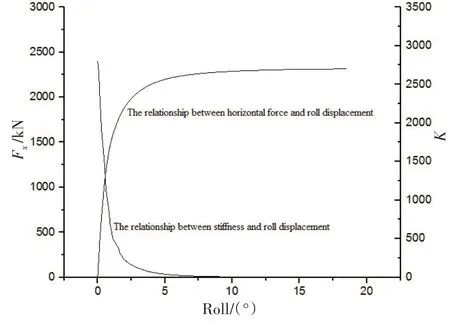
图6 水平集中力/刚度与横摇角度的关系Fig.6 Relationship between horizontal force/stiffness and roll displacement

2.4 吸力桩在弯矩My作用下的承载力分析

吸力桩在弯矩My作用下的承载力分析，从平台的运动角度上看，就是浮力塔在弯矩作用下吸力桩横荡与横摇耦合运动的承载力分析。其P-S曲线结果如图7 与图8 所示，其中图7 列出了弯矩与横荡的位移关系，而图8列出了弯矩与横摇的位移关系。

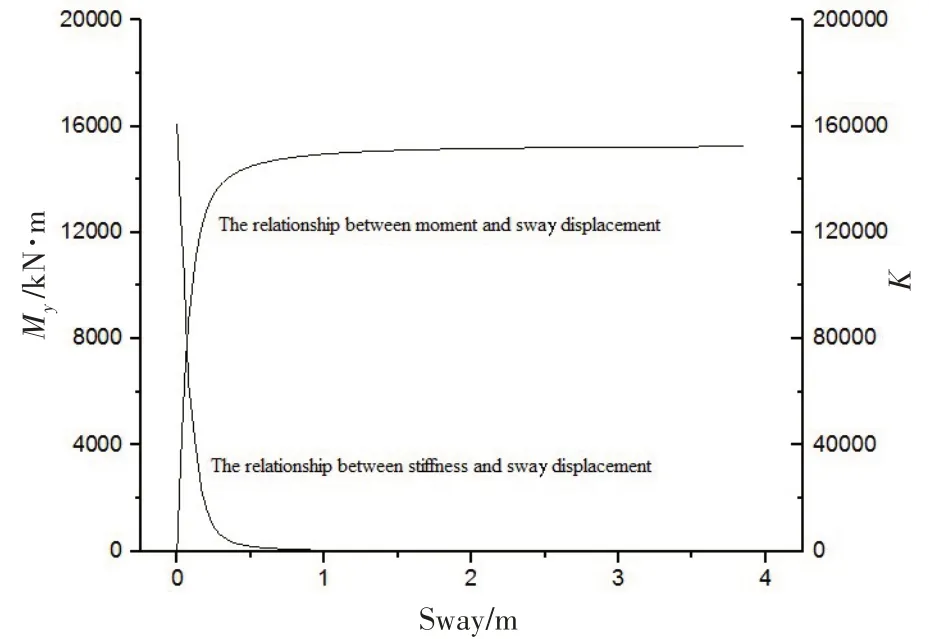
图7 弯矩/刚度与横荡位移的关系Fig.7 Relationship between moment/stiffness and sway displacement

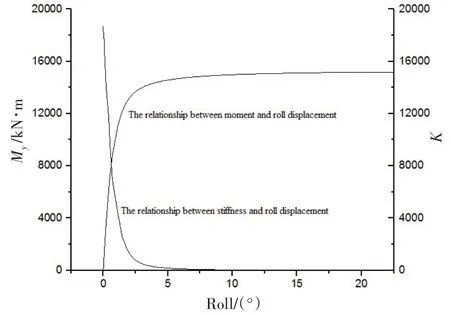
图8 弯矩/刚度与横摇角度的关系Fig.8 Relationship between moment/stiffness and roll displacement

图7 和图8 保持了高度一致的关系，并且与图4 有着相似的性质，即存在陡变段、过渡段及缓变段。从图中可以看出，大约在受到12 000 kN·m 时，承载力曲线与刚度曲线逐步进入过渡段，也就是说，桩基周围的土层塑性变化逐步增加直至完全进入塑性破坏阶段。12 000 kN·m对应的桩基横荡位移大约是0.2 m 左右，横摇角度大约为2.0°。依据前面的分析，结合承载力曲线及刚度曲线可以判断出，吸力桩在安全的范围内工作。

3 土弹簧刚度矩阵与运动验证

在得出浮力塔吸力桩的P-S曲线后，可以将承载力转化为土弹簧的约束刚度。其中升沉运动下吸力桩P-S曲线可以取陡变段直接通过胡克定律求得吸力桩受到升沉方面的约束刚度。而吸力桩受到的横荡约束、横摇约束以及横摇横荡耦合约束则需要通过水平力作用下吸力桩横荡横摇耦合运动P-S曲线与弯矩作用下吸力桩横荡与横摇耦合运动P-S曲线联立求解。现只考虑横荡、横摇以及横摇横荡耦合约束作用，故将式（1）简化为

根据上面的分析结果可知，浮力塔吸力桩均在安全的范围内工作，所以可以用吸力桩承载力P-S曲线陡变段上的某一点，即取图5 至图8 曲线中的某一点，用该点对原点的斜率近似为曲线的割线斜率来进行约束刚度计算。在水平力作用下吸力桩横荡横摇耦合运动P-S曲线中的陡变段，取一个作用力F1，得出对应的吸力桩水平运动幅值X1和转动幅值θ1，将这3 个值代入式（2）可得式（3）的前两个方程。在弯矩作用下吸力桩横荡横摇耦合运动P-S曲线中的陡变段，取一个作用弯矩M2，得出对应的吸力桩水平运动幅值X2和转动幅值θ2，将这3 个值代入式（2）可得式（3）的后两个方程，由于取值均在陡变段，吸力桩周围的土层均处在弹性阶段，可以假设横荡约束、横摇约束以及横摇横荡耦合约束3个刚度保持不变，所以可以将这4个方程联立求解如式（3）所示：

求解式（3），可以得到横荡约束、横摇约束以及横摇横荡耦合约束4个刚度如式（4）～（7）所示：

由于约束刚度矩阵是对称阵，所以从理论上讲，k24与k42得出的结果应该一致。并且浮力塔在横摇和纵摇方向对称，所以纵荡、纵摇以及纵荡纵摇耦合约束刚度与上述横荡、横摇以及横荡横摇耦合约束刚度一致。

首先分析k22、k44、k24和k42，依据之前的分析，F1的取值不能大于1750 kN，而M2的取值不能大于12 000 kN·m，考虑到即使土弹簧未进入过渡段，其刚度也存在着非线性，即周围土层存在着塑性变化，并且考虑到实际运动的情况，平台运动最大值的出现频率并不高，所以用1750 kN 与12 000 kN·m来取土弹簧刚度并不合适，进而取上述值约60%左右即F1=1000 kN，M2=8000 kN·m 时的数据，进行土弹簧刚度分析。在图5至图8曲线中取值如表3所示，由式（4）至式（7）求得各约束刚度如表4所示，可以看出横荡横摇的耦合刚度k24与横摇横荡的耦合刚度k42偏差极小，两者距其平均值相差0.867%，这也验证了k24与k42的结果应该一致的结论。两者细微的差别是由于土的非线性程度造成的，由于取值均在陡变段，并且F1与M2取值均处于曲线陡变段的中部，对应土塑性变形所占总变形的成分接近，所以k24与k42偏差极小，这也验证了表3取值的合理性。

表3 刚度计算取值Tab.3 Values for calculation of stiffness of soil springs

表4 刚度计算结果（kN/m）Tab.4 Results of stiffness of soil springs (kN/m)

然后分析k33，依据之前的分析，Fz的取值不能大于8000 kN，同上所述，取Fz=6000 kN，在图4 曲线中取值如表3所示，由k=Z/Fz可直接求得刚度k33，如表4所示。

将如上刚度代入式（1）并基于HydroStar 进行运动模拟，典型的横摇RAO 如图9 所示，纵摇的RAO 与横摇一致。将CX-15 所在海域百年一遇的波浪条件Hs=3.8 m 和Tz=20 s 结合横摇RAO 进行运动分析，得出平台在百年一遇的波浪中摇动角度有义值为2.1°，结合图6 与图8 可以看出，这个运动值在吸力桩的安全范围内。将CX-15 所在海域一年一遇的波浪条件Hs=1.5 m 和Tz=13 s 结合横摇RAO 进行运动分析，得出平台运动平均值为0.42°，有义值为0.67°，极大值为1.29°，其中遭遇一年一遇波浪的情况下，平台运动谱分析平均值与表5所示的平台实际运营的观测结果基本吻合（横摇计算值为0.42°，2017年10月横摇实测值为0.47°）。

图9 CX-15横摇RAOFig.9 Roll RAO of CX-15 platform

表5 浮力塔平台CX-15在2017～2018年运动实测结果Tab.5 Rolling results of first buoyant tower CX-15 in 2017-2018

4 结 论

本文以首制浮力塔平台CX-15为研究背景，研究了平台吸力桩的承载力以及对平台的运动约束。基于现场海域的土壤取样，通过三轴压缩试验获得土样的参数；选取修正剑桥模型为土的本构模型，通过Abaqus 进行三维模拟得出了吸力桩的承载力曲线，并将承载曲线转化为土弹簧的约束刚度，并基于该约束刚度通过HydroStar进行浮力塔的运动分析，得出如下结论：

（1）浮力塔吸力桩承载力的分析要充分结合运动的实际情况，分析工况包括升沉运动下的承载力和横荡横摇耦合运动下的承载力，对比CX-15平台现场观测结果与P-S曲线可以看出，浮力塔吸力桩在安全的范围内工作；

（2）通过P-S曲线可以获得土层对吸力桩的约束刚度，约束刚度的分析需基于曲线的陡变段，该阶段土层处于弹性阶段，分析的结果中土的非线性效应不大；

（3）基于约束刚度矩阵进行运动分析，从结果可以看出，浮力塔在百年一遇的波浪下吸力桩也能在安全的范围内工作，并且预报的结果与CX-15平台现场观测的结果吻合度较高，说明该约束刚度矩阵是合理的。