深水吸力桩建井过程及承载力特性的试验研究*

刘书杰 黄 熠 刘和兴 张明贺 李 磊 郑金龙

(1.中海石油(中国)有限公司湛江分公司 2.中国石油大学(北京)安全与海洋工程学院)

0 引 言

吸力桩的桩体是一个顶端封闭、底部开口的钢筒，又称筒形基础，是一种常见的海洋工程基础形式。多数筒形基础采用负压下沉安装，合理的负压能在保证地基稳定的前提下大幅度减小筒体下沉阻力。吸力桩早期主要应用于深海锚固及海底地质勘测等水下工程，对其表层建井技术的应用及研究较少。1980年，在欧洲北海的40 m水深海域处吸力桩首次安装了单点系泊储油装置；1989年，挪威国家石油公司研制开发了吸力桩式基础的导管架平台，并于1994年在挪威70 m水深海域成功运用筒形基础安装了导管架平台[1]；1994年7月，在中国渤海首次安装了吸力锚为油轮系泊定位，并于1995年成功运用了双筒式吸力锚，第一次为“自强号”沉垫自升式平台安装吸力式阻滑桩；1999年在渤海海域成功安装了自主建造的三筒吸力桩系缆平台；2000年以后，挪威多次在北海进行吸力桩建井实践，并于2018年在澳大利亚海域成功实现了近1 500 m水深的吸力桩建井和回收作业；2020年，中石油成功利用吸力桩表层建井的优势进行了天然气水合物的第二次试采，证明了吸力桩建井的应用前景。

2011年，T.SIVERTSEN等[2]提出新的海底建井基础概念，给出了吸力桩的设计思想。2013年，闫澍旺等[3]通过数值模拟的方法对海上风电机组筒形基础的承载力特性进行了研究，包括长径比、水平承载力以及桩体内部设置隔舱的承载力特性，给出了吸力桩基础承载力的影响因素。2013年，李大勇等[4]提出在传统吸力基础上外加桩裙的复合基础结构，可显著提高基础水平承载力。丁红岩等[5]针对海上风电复合筒形基础在粉质黏土中的下沉进行大尺寸试验，分析了沉贯过程中的土体压力和孔隙水压力，并给出了沉贯摩擦因数的取值，但计算方法较为复杂。W.MATHIS等[6]提出在挪威巴伦支海域进行吸力桩建井技术，取得了针对浅层油气藏开发实践的成功。KAN C.B.等[7]提出一种新型复合基础来安装表层导管，在常规表层导管外部附加一个大直径的筒形基础，并通过竖直模拟的方法证明了该种复合结构可以提高海底井口的竖向承载力和抗弯性能。该方法并没有改变表层导管的下入深度，设计过于保守，只是在井口附近外加大直径筒形基础，并依靠基础自重下入海底浅层，这既增加了制作和安装成本，也存在复合基础下入受阻的风险，但这种思想与吸力桩方法建井原理相同。马文冠等[8]针对粉土中筒形基础的贯入阻力进行研究，给出了计算方法，并针对不同筒端形式的减阻效果进行分析，为吸力桩建井的减阻设计提供了参考。

本文基于上述研究，对深水吸力桩建井方法开展沉贯过程承载力特性理论和试验研究，以期为深水吸力柱建井施工及后续承载力计算提供技术指导。

1 吸力桩法建井

1.1 吸力桩筒形基础

筒形基础是一种圆筒形薄壳结构，通常采用钢质单筒。筒形基础入泥后，依靠土对其侧壁的摩擦力及底部支撑力提供竖向承载力。传统深水海底建井采用表层导管基础，适用于多数土质，下入深度一般大于60 m，用钢量大，海上安装用时长。吸力桩基础入泥浅，可节省导管钢材，承载能力强。

吸力桩利用桩体自身重力沉入海底，再通过吸力泵抽出筒内海水和空气，制造内外部压力差，最终被贯入到设计深度。国内外对于深水表层建井中表层导管的承载性能、筒形基础的承载性能等都做了大量研究。将深水导管与筒形基础进行组合，形成一种新型复合结构，利用筒形基础的承载特性给井口提供支撑的研究较少。由于外部筒形基础的承载能力较强，从而增强了导管在竖直方向上的承载能力以及在井口伸出部分的抗弯性能。这种深水表层建井施工方式，大大缩短了导管下入深度，导管下入后不需要承载力恢复时间，提升了下导管效率，降低了钻井费用。

1.2 吸力桩建井过程

采用吸力桩方法下表层导管的过程如图1所示，具体步骤如下。

图1 吸力桩建井过程示意图

(1)工程船将预制好的吸力桩基础运输到建井位置，通过揽绳将吸力桩送入海底泥线以上位置，准确调整下入位置，控制下入垂直度，为吸力桩入泥做准备。

(2)海底浅层主要为松软泥土，吸力桩下入初期阻力较小，吸力桩自身浮重为800 kN左右，可以依靠自身重力作为下入动力，重力贯入深度大约3 m。此时为了确保下入垂直，应保持缆绳处于受拉状态。

(3)通过绳索将带有抽吸功能的机器人下入海底泥线附近，将抽吸泵连接到抽吸口，逐渐抽出吸力桩内部海水和空气，此时由于吸力桩顶部内外的压力差将吸力桩逐渐压入海底地层，随着吸力桩下入海底地层，内部环空体积逐渐减少，吸力桩的下入阻力逐渐增加，所以抽吸排量与吸力桩的下入速度需要合理匹配才能保证吸力桩安全下入。

(4)吸力桩在抽吸泵的抽吸压力下下入海底地层预定深度，若中途出现下入倾斜问题可以通过抽吸泵加压的方式使吸力桩上提一定距离重新下入，直至垂直下至目的位置。

(5)在吸力桩下入到位后，通过送入工具将表层导管喷射或钻入中心管，通过水泥浆固井的方式将表层导管与中心管进行连接，但不依靠固井质量来提供承载力，所以无需等待水泥浆固结时间。也可以在吸力桩下入之前把表层导管与吸力桩进行提前固定，同时下入海底地层。

2 吸力桩法建井的承载力模型

2.1 吸力桩基本参数

吸力桩的主要参数为吸力桩的外径D、长度L、壁厚d、质量G、浮重G1、中心管直径D1、中心管厚度d1。环境条件为水深L3，海底地层土体的不排水抗剪强度Su随海底泥线以下的深度h变化，即Su=p(h)。下入绳索的基本要求为满足拉力大于G，下入深度大于L3。

结合海底浅层土体的CPT取样研究分析，可以得到海底土体不排水抗剪强度随海底泥线以下深度的变化关系，即已知Su=p(h)，在重力下入阶段可以结合土体及下入深度等参数进行吸力桩底部支撑力与侧向摩阻力计算，并可研究其比例关系，由此进一步对吸力桩与周围土体的侧向摩阻力系数α和底部支撑力系数β进行推算，以指导后续沉贯操作。

2.2 重力沉贯过程

对吸力桩重力沉贯过程进行受力分析，如图2所示。图2中，l为吸力桩重力贯入过程中在土体中的安装深度。

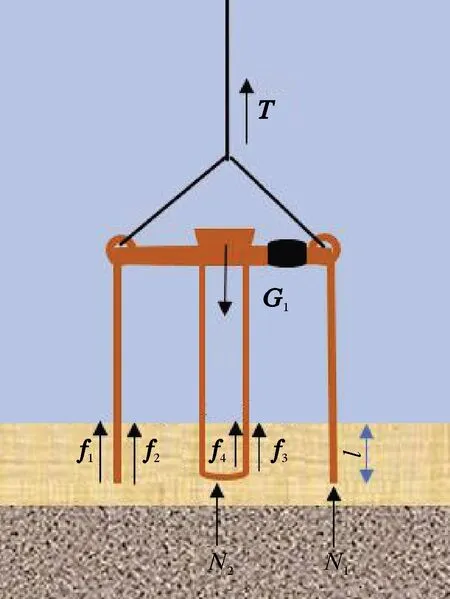
图2 重力贯入阶段受力分析

由受力平衡可得：

G1=T+f1+f2+f3+f4+N1+N2

(1)

式中：T为绳索竖直向上的拉力，kN；f1、f2、f3及f4分别为吸力桩外壁、吸力桩内壁、中心管外壁、中心管内壁与地层土体的轴向摩阻力，kN；N1、N2分别为地层土体对吸力桩和中心管下端面的底部支撑力，kN。

由于吸力桩依靠重力下入到位后绳索基本不提供竖直向上的拉力，所以T可以忽略不计，则式(1)变为：

G1=f1+f2+f3+f4+N1+N2

(2)

由地层土体不排水抗剪强度、已知的CPT取样、未知的吸力桩与土体的侧向摩阻力系数α和底部支撑力系数β分别可得：

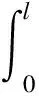
(3)

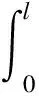
(4)

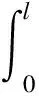
(5)

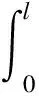
(6)

(7)

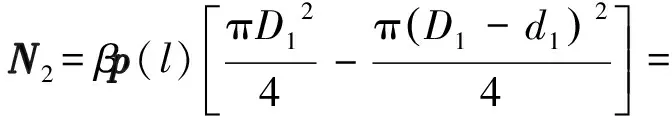
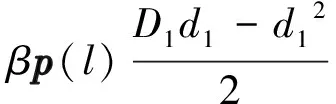
(8)

由于存在未知数α和β，所以采取上提吸力桩的方法测得上提拉力：

T=G1+F

(9)

式(9)中，已知G1，可求出总侧向摩阻力F，从而进一步求出α。总侧向摩阻力F与总底部支撑力N的关系式为：

G1=F+N

(10)

总底部支撑力计算式为：

N=N1+N2

(11)

结合式(7)、式(8)及式(11)，可计算出底部支撑力系数β。

求得侧向摩阻力系数α和底部支撑力系数β，可为后续承载力计算和合理下入深度设计提供理论参数支撑。

2.3 抽吸沉贯过程

在连接抽吸泵之前，吸力桩内外连通，没有压力差。连接抽吸泵后吸力桩内部海水被抽出(见图3)，当内外压差所提供的下压力大于下入阻力时，吸力桩开始向下运动。

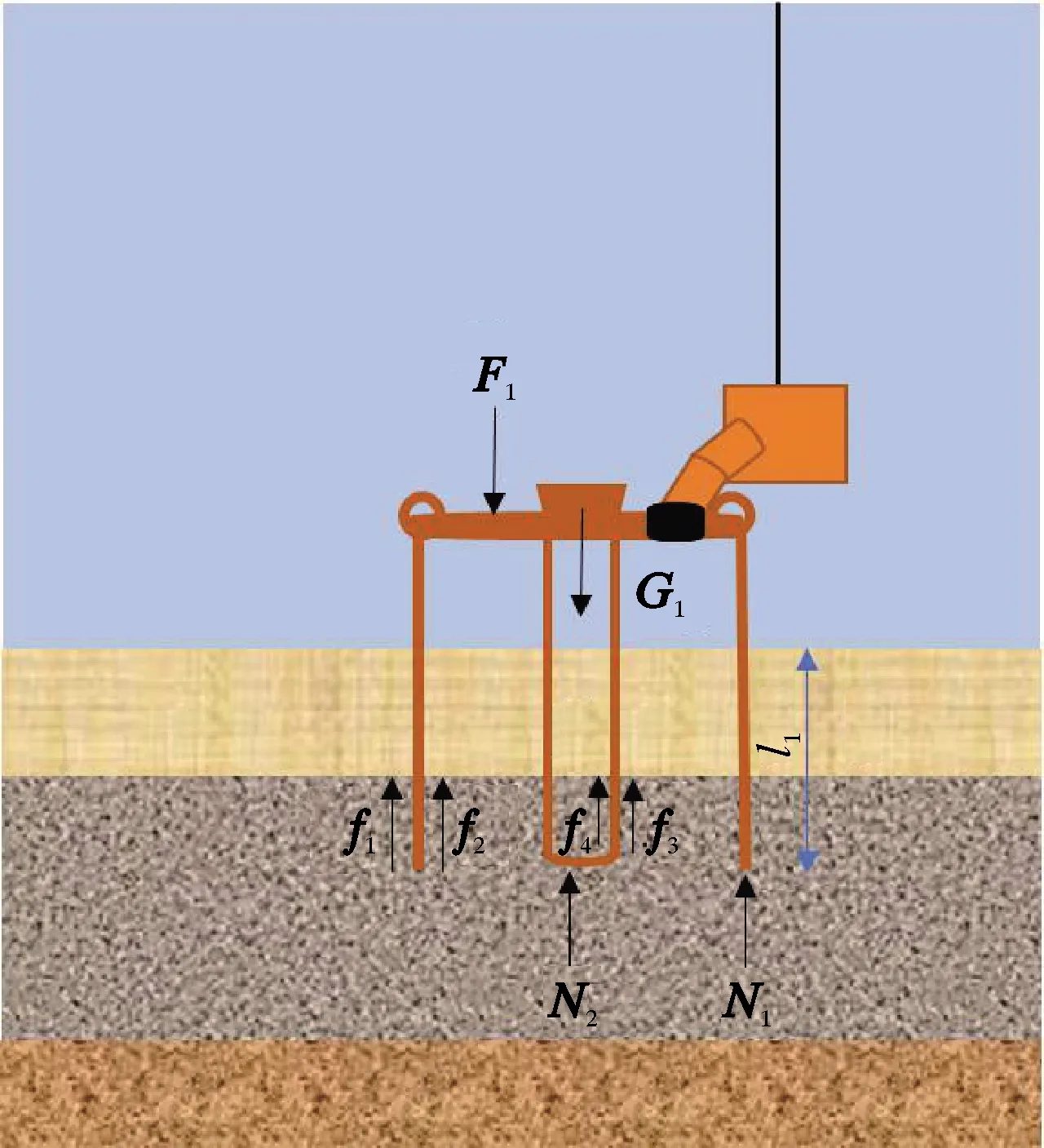
图3 抽吸贯入过程受力示意图

下入初期需要较小的排水空间，吸力桩内外压力差为：

Δp=p1-p2

(12)

p1=ρgL3

(13)

式中：p1为吸力桩外部压力，kPa;p2为吸力桩内部压力，kPa。

p2取最大值为大气压,最小值为真空条件，压力为0，桩体内外压力差形成的下压力为：

F1=ΔpS

(14)

式中：S为桩体端面面积，m2。

吸力桩所受各力关系为：

G1+F1>f1+f2+f3+f4+N1+N2

(15)

由此可以计算出吸力桩与中心管所受侧向摩阻力f1、f2、f3及f4，以及地层土体对吸力桩与中心管的底部支撑力N1、N2，具体计算如式(16)～式(21)所示。

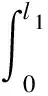
(16)

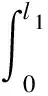
(17)

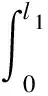
(18)

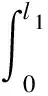
(19)

(20)

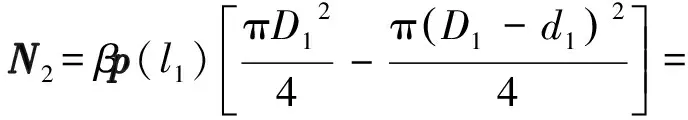
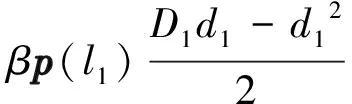
(21)

式中：l1为吸力桩抽吸贯入过程中在土体中的安装深度，m。

结合水深、吸力桩尺寸及抽吸泵功率等参数可以计算吸力桩能否下入到预定深度。吸力桩下入预定深度后解脱抽吸泵，提高吸力桩内压，使得内外压力保持平衡，有助于提高竖向承载力。

吸力桩下入到位后，需要将表层导管通过喷射方法下入到吸力桩的中心管中，此时吸力桩中心管内部土体被破坏，吸力桩承载力略有降低，但对整体承载力不造成影响，表层导管坐挂到吸力桩中心管上，注入水泥浆封固，但不依靠水泥浆提供承载力。此时吸力桩竖向承载力增加了表层导管和水泥浆的重力。

3 吸力桩法建井的试验研究

3.1 试验原理

吸力桩表层建井的下入过程需要进行模拟试验研究。试验场地在中国石油大学(北京)室内实验室，试验装置如图4所示。

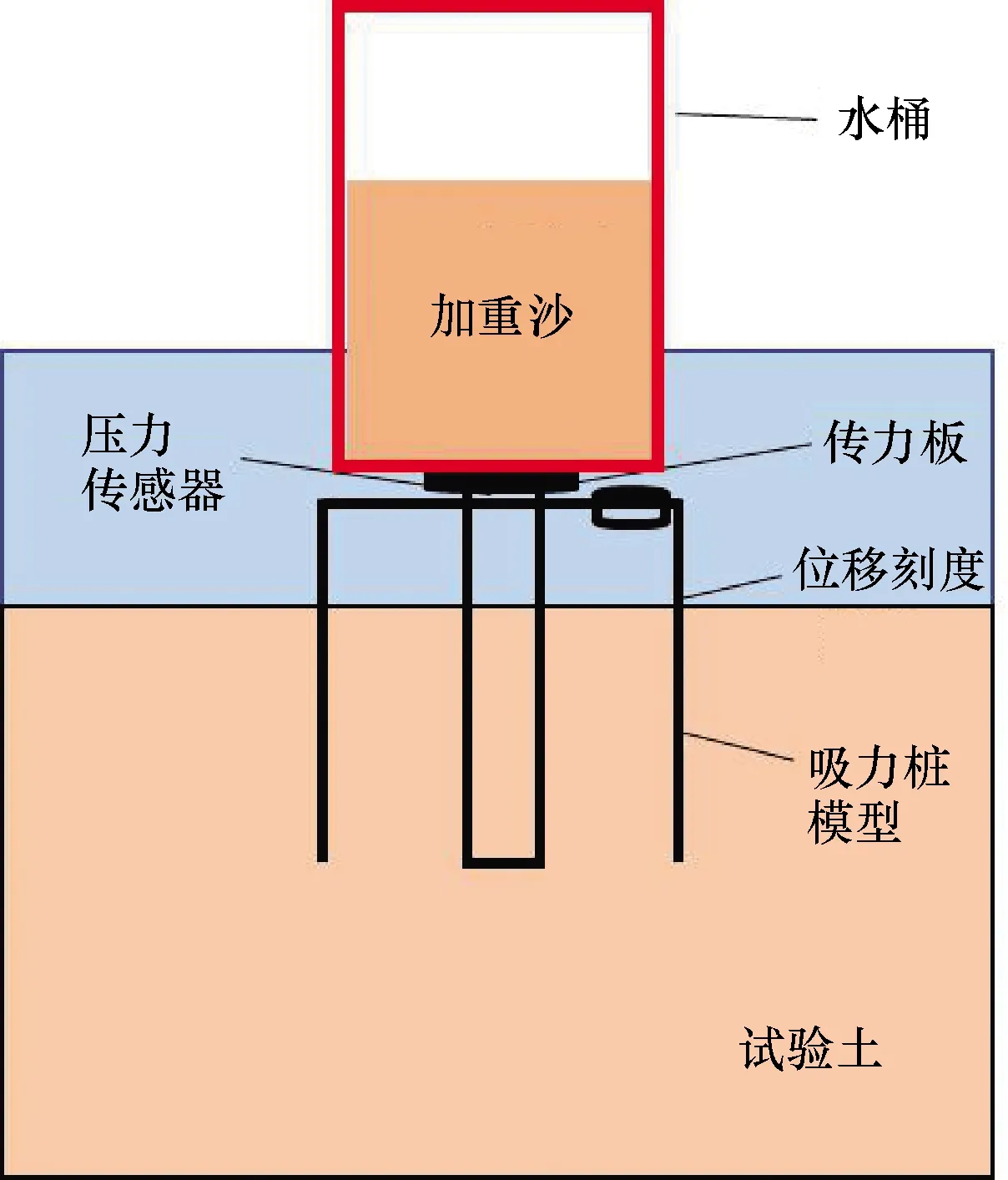
图4 试验装置示意图

现场吸力桩下入需要外接抽吸泵，但很难模仿现场海水深度条件，所以采用顶部添加沙土逐渐加压到深水条件所能提供的最大压差。同时也可以增加模型初始顶部压力来解决模型重力较小而使初始贯入深度不足的问题。

吸力桩的主要特性参数为端面半径r及长度L，其中贯入动力主要与端面面积πr2成正比，贯入阻力主要与侧面面积2πrL成正比。由此得出吸力桩的长径比L/r是影响贯入过程的主要参数，所以可以将吸力桩进行任意相似比例缩小，并不影响贯入规律。水合物试采的吸力桩实物直径为6 m,长度10 m,质量约80 t，长径比约为3，故本试验模型在设计长径比区间0～5进行贯入特性研究，以满足现场设计要求。

设计模型的直径约为20 cm，缩尺比约为30，所以质量缩尺比约为27 000，由此得模型的质量约为3 kg，本设计模型吸力桩质量满足缩尺比要求。

3.2 土样制备

(1)深海浅层土的土质松软，以黏性土为主，试验选用的是渤海浅层黏性土，使用之前，先将土提前晾干并粉碎固结土块，保证在试验时土质均匀。

(2)去除杂质，保持土样均质。将试验用土中的砂砾挑出，将胶结块打碎，使土比较均匀。

(3)将试验黏土填入所用的容器。为了使试验土层达到饱和度要求且均匀，采用分层填入的方法，每填入0.2 m厚度的土样，加水后振捣均匀，再填入下一厚度的土样，直至黏性土层总厚度达到1 m，再向试验池加水，直至水淹没土。

土样配置完成后(见图5)，测得深度为1 m的土体的不排水抗剪强度随土体深度的变化关系如图6所示。从图6可见，红色曲线为拟合关系线，近似为对数关系，测得浅层20 cm以内的土体抗剪强度较小，为计算方便，取值为1 kPa。

图5 试验用土

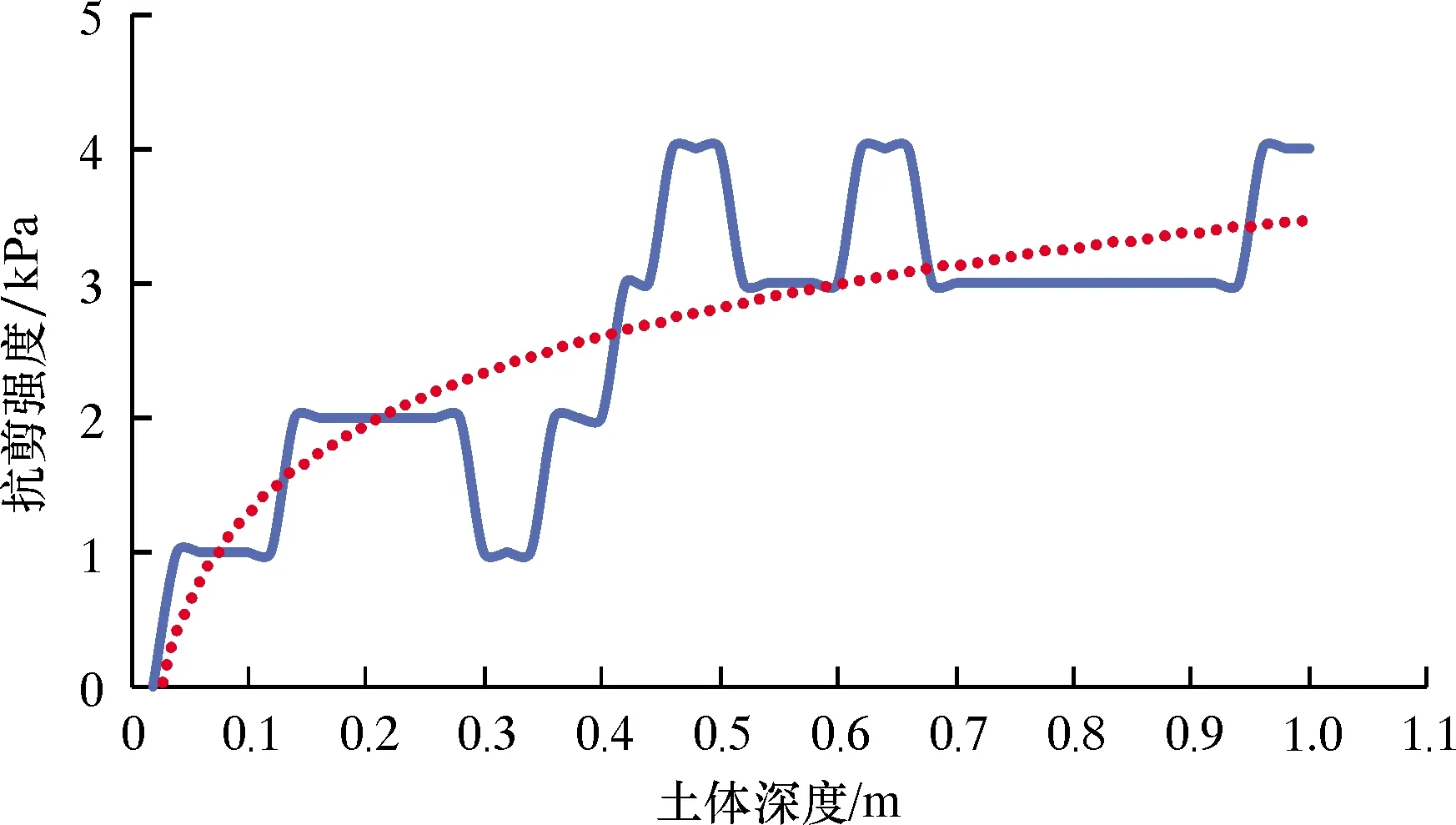
图6 海底浅层土体强度

3.3 试验过程

设计吸力桩尺寸(直径×长度)分别为：20 cm×35 cm、25 cm×25 cm、30 cm×15 cm、35 cm×10 cm共4种尺寸进行模拟试验。图7为吸力桩模型图。

图7 吸力桩模型示意图

在吸力桩模型重力相近的条件下进行模拟试验，寻找吸力桩下入过程中侧向摩阻力和底部支撑力的大小关系，以及预测下入过程中的侧向摩阻力系数和底部支撑力系数的估算值[9-12]。此处设计吸力桩模型的质量约为3 kg。

将吸力桩上部添加质量一定的重物，此试验选择内部添加一定体积的沙的水桶代替重物，优点是方便调节重物的质量，探索合适的配重，最终选择配重质量分别为2、3、4及5 kg。在相同配重下，分别测量不同直径的吸力桩模型的重力贯入深度，并通过测力计上拔吸力桩模型的最大力来求解吸力桩与试验土体的侧向摩阻力。试验装置及过程示意图如图8所示。

图8 吸力桩贯入及上拔试验装置示意图

试验过程中，每一个模型进行单独测量，不考虑群桩效应的影响，桩体边界效应在1倍桩径范围内最为显著，大于3倍桩径几乎没有影响。为了降低边界效应对试验结果的影响，特别设计水池的尺寸大于3倍模型直径，由于模型尺寸较小，试验过程静置时间充足，所以在误差允许范围内可以忽略边界效应的影响。

4 试验结果及分析

4.1 模型下入深度及上拔力

不同直径的吸力桩模型在不同外加载荷的作用下贯入深度如图9所示。从图9可见，随着外加载荷的增加，相同直径吸力桩模型下入深度逐渐增加，且相同加重块条件下随着模型直径增加，下入深度逐渐降低，变化关系类似指数关系[13-16]。

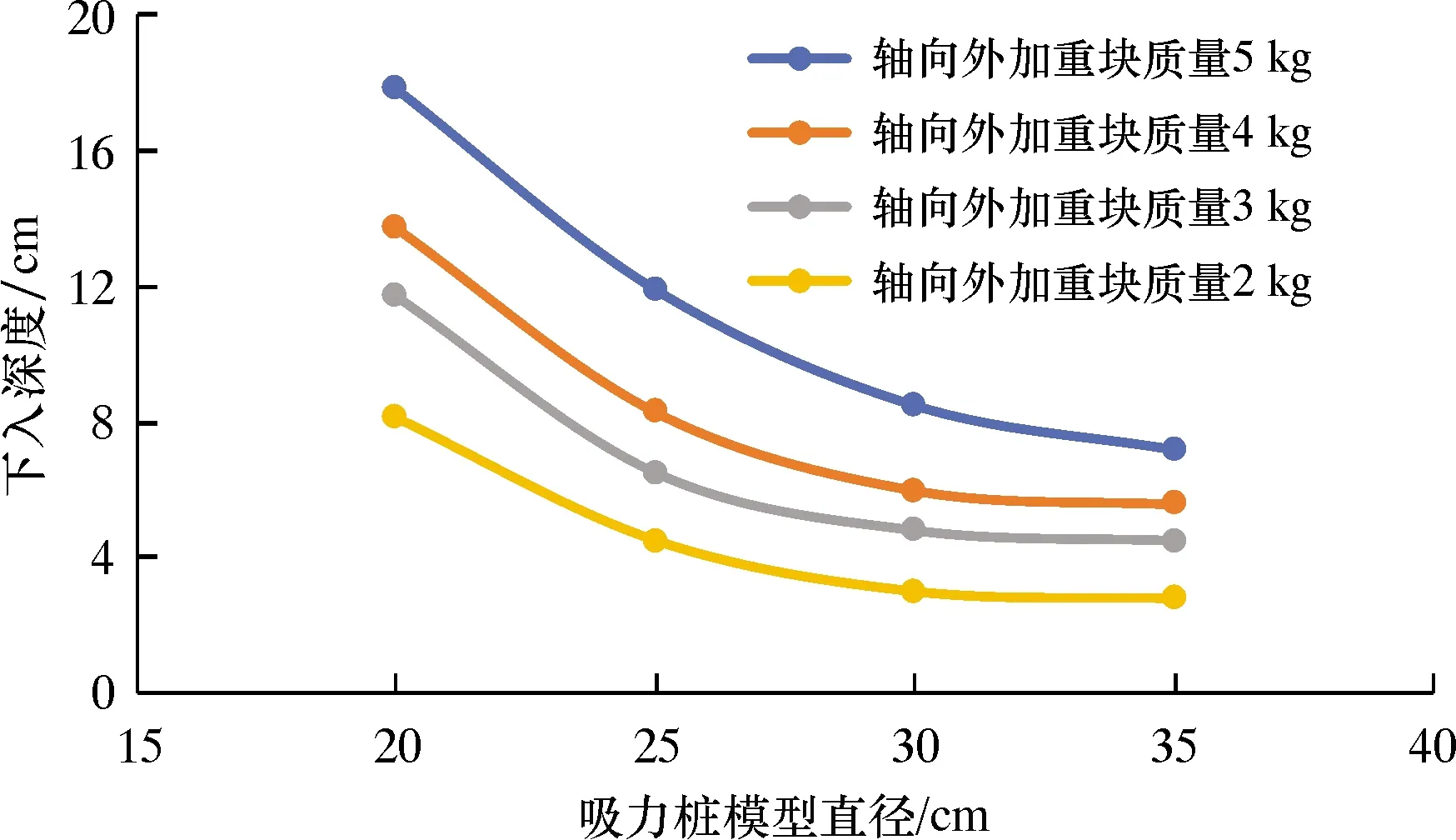
图9 下入深度随吸力桩模型直径的变化关系

吸力桩模型在外加载荷作用下，贯入到极限深度后，将上部重物取下，利用电子测力计分别测量每组试验吸力桩缓慢上拔的初始最大值，上拔力随吸力桩模型轴向外加载荷及其直径变化关系分别如图10和图11所示。

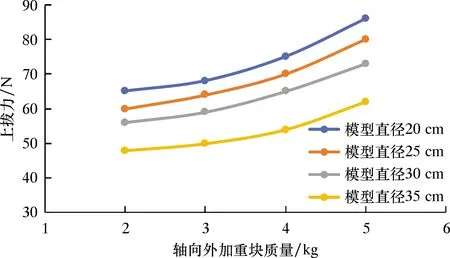
图10 上拔力随吸力桩模型轴向外加载荷的变化关系

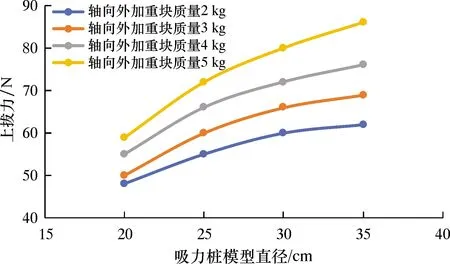
图11 上拔力随吸力桩模型直径的变化关系

由图10可见，随着作用在吸力桩模型上部加重块质量的增加，相同直径的吸力桩模型的上拔力呈指数关系增加，且处于缓慢增加阶段[17-18]。

由图11可见，相同加重块质量的吸力桩模型上拔力随着吸力桩模型直径的增加呈现类似对数关系增加。

4.2 模型侧向摩阻力和底部支撑力

通过式(9)～式(11)计算得出侧向摩阻力和底部支撑力，如图12和图13所示。

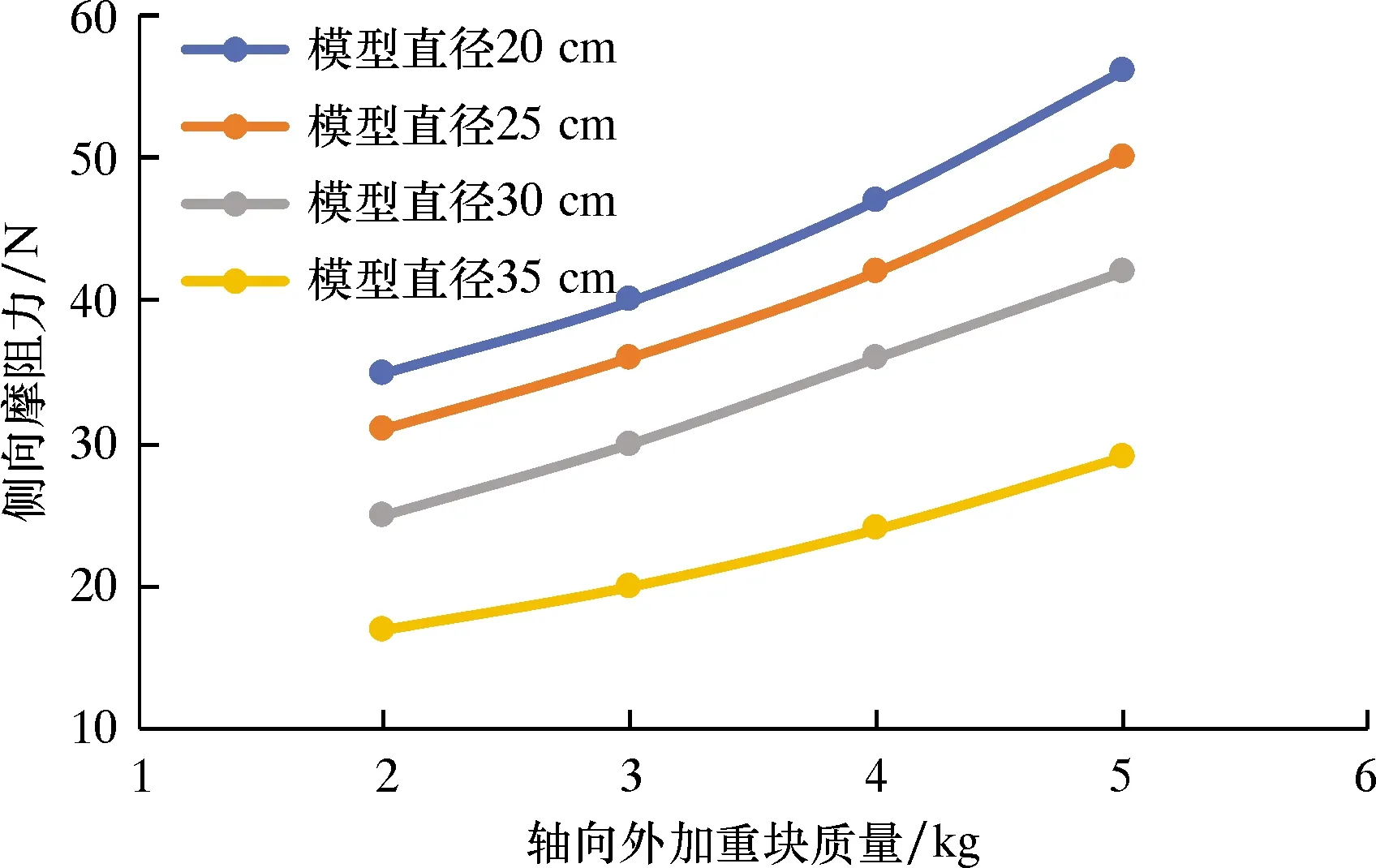
图12 吸力桩模型侧向摩阻力随轴向外加重块质量的变化关系

图13 吸力桩模型底部支撑力随轴向外加重块质量的变化关系

由图12可见，相同直径吸力桩模型侧向摩阻力随着加重块质量的增加呈类似指数关系增加，在相同加重块质量条件下，直径越小，模型侧向摩阻力越大。

由图13可见，相同直径吸力桩模型底部支撑力随着加重块质量的增加呈类似对数关系增加，且在相同加重块质量条件下，直径越大，吸力桩模型底部支撑力越大[19-21]。

下面探讨不同模型条件下侧向摩阻力与底部支撑力的比例关系。通过对试验数据进行处理，得到不同直径吸力桩模型在不同外加轴向载荷的条件下的底部支撑力和侧向摩阻力数值和比例关系，如表1所示。

表1 不同直径吸力桩模型底部支撑力和侧向摩阻力及其比例关系

根据表1，可得不同直径吸力桩模型在不同工况下的侧向摩阻力和底部支撑力的相对关系，如图14所示。

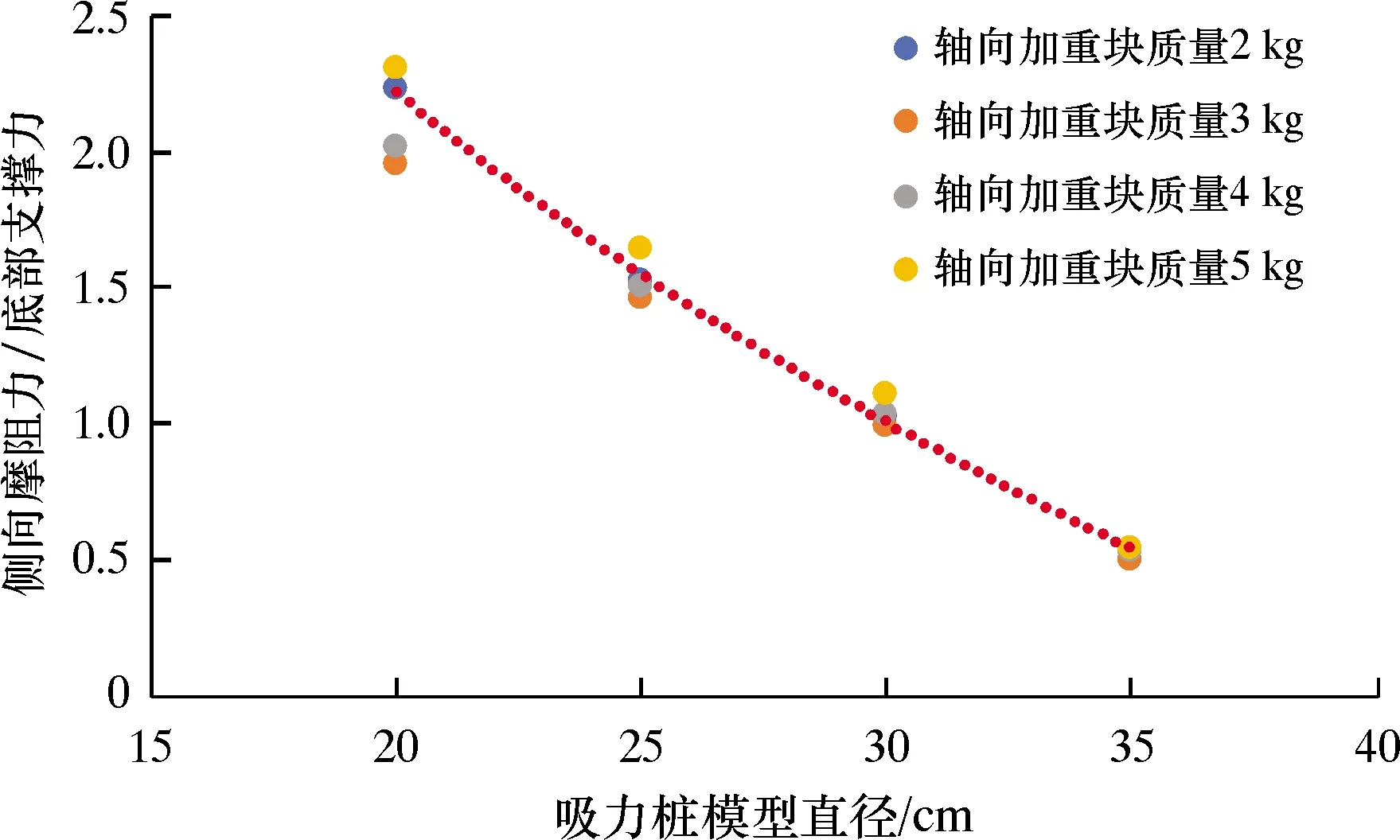
图14 侧向摩阻力与底部支撑力比值随吸力桩模型直径的变化关系

因为模型直径的增加，导致桩体下入深度降低，浅部土体抗剪强度较低，所以侧向摩阻力占总承载力比例降低，底部支撑力占总承载力比例提高。由于本试验过程中试验组数较多，土体逐渐压实，模型质量较小，模型内土塞明显，所以出现底部支撑力阻力大于侧向摩阻力的现象。试验结果表明，侧向摩阻力与底部支撑力的比值与吸力桩直径有关，且随着直径的增加其比值呈类指数降低，外加载荷大小对比值影响不大。

4.3 承载力系数

关于土体的抗剪强度，此处结合图6取保守值p(h)=0.001 MPa,吸力桩模型壁厚2 mm，中心管直径6 cm, 壁厚2 mm。

结合式(3)、式(4)、式(18)及式(19)，根据吸力桩直径、壁厚、土体性质、侧向摩阻力及下入深度等因素进行不同直径吸力桩模型侧向摩阻力系数求解。

以20 cm直径吸力桩模型为例计算侧向摩阻力系数。吸力桩长35 cm，壁厚2 mm，质量3 kg；中心管直径6 cm, 壁厚2 mm。在上部加重块质量5 kg条件下，下入深度17.4 cm，采取土体抗剪强度恒定取值为0.001 MPa,侧向摩阻力为55.8 N，总侧向摩阻力计算式为：

F=f1+f2+f3+f4=απ(D+D1)p(h)l+

απ(D+D1-d-d1)p(h)l=

απ(2D+2D1-d-d1)p(h)l

(22)

将数值代入式(22)，求得α=0.256。

同理，结合图6不同深度的土体抗剪强度，求出不同条件下的侧向摩阻力系数与外加载荷和吸力桩模型直径的关系，如图15和图16所示。

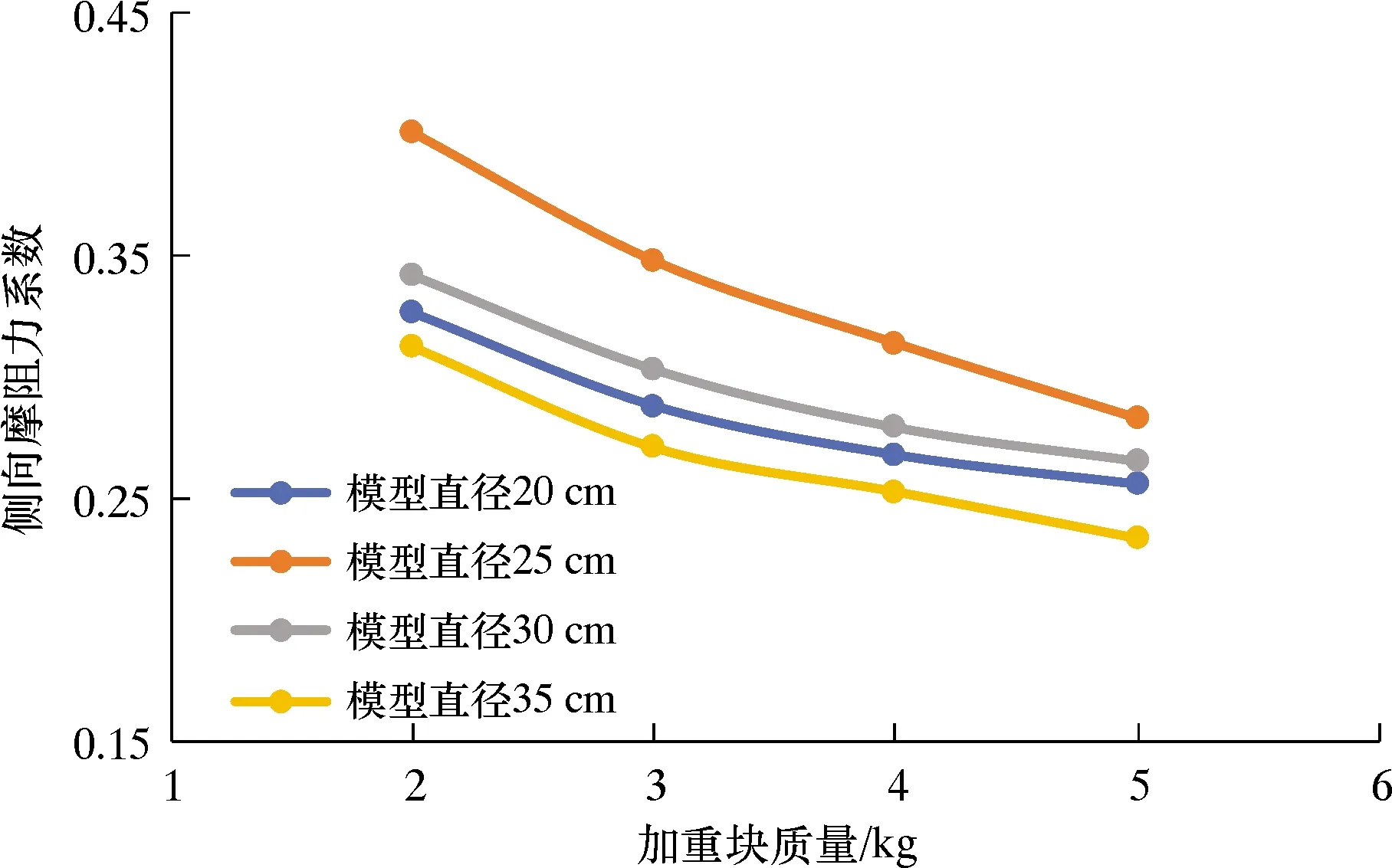
图15 侧向摩阻力系数随吸力桩模型外加重块质量的变化关系

图16 侧向摩阻力系数随吸力桩模型直径的变化关系

从图15可以看出，随着吸力桩模型外加重块质量的增加，侧向摩阻力系数的计算值呈降低趋势。随着加重块质量的增加，模型下入地层深度增加，选取的地层承载力较大，所以导致计算结果偏低，正常情况下需要针对不同深度土体强度进行积分运算，此处近似值与真实值相比偏低。

从图16可见，在相同外加载荷条件下，吸力桩模型的侧向摩阻力系数随着吸力桩模型直径的增加先增加后降低，呈类似二次函数的抛物线关系，抛物线存在该系数的理论最大值，可以根据设计尺寸尽可能充分利用侧向摩阻力来提高承载力。由于试验过程中存在测量时间的差距，存在侧向摩阻力的时间效应影响因素，且此模拟试验只是探索规律来指导工程实践，所以可能存在由模型缩尺所带来的规律性偏差，但该研究方法可以为后续研究提供经验。

底部支撑力系数计算式为：

(23)

同理，可计算不同尺寸吸力桩模型底部支撑力系数。在求解底部阻力系数时发现，如果假设模型底部的受力面积为底面壁厚部分面积，计算承载力与实际不符，这可能是由于土体内部的相互作用导致桩体与内部土体连接为一体，在上拔过程中不能提供有效承载力，但在下压过程中，实际提供底部支撑的面积更接近于整个圆面。根据API标准，桩体底部承载力为土体不排水抗剪强度的9倍，但此处由于吸力桩直径较大，不采用上述标准。

综上所述，提出新方法：求解β时假设底面受力为圆形。此假设在国外已经有学者和相关石油公司提出，但在大型筒形基础上的应用还没有理论研究，所以通过此模拟试验来验证其合理性。相关计算式为：

(24)

在此试验中可得出更合理的β值。

同样以20 cm直径的吸力桩模型为例，由式(24)计算得β=0.335。

同理，结合图6中不同深度的土体抗剪强度，求出在不同条件下的底部支撑力系数与外加载荷和吸力桩模型直径的关系，如图17和图18所示。

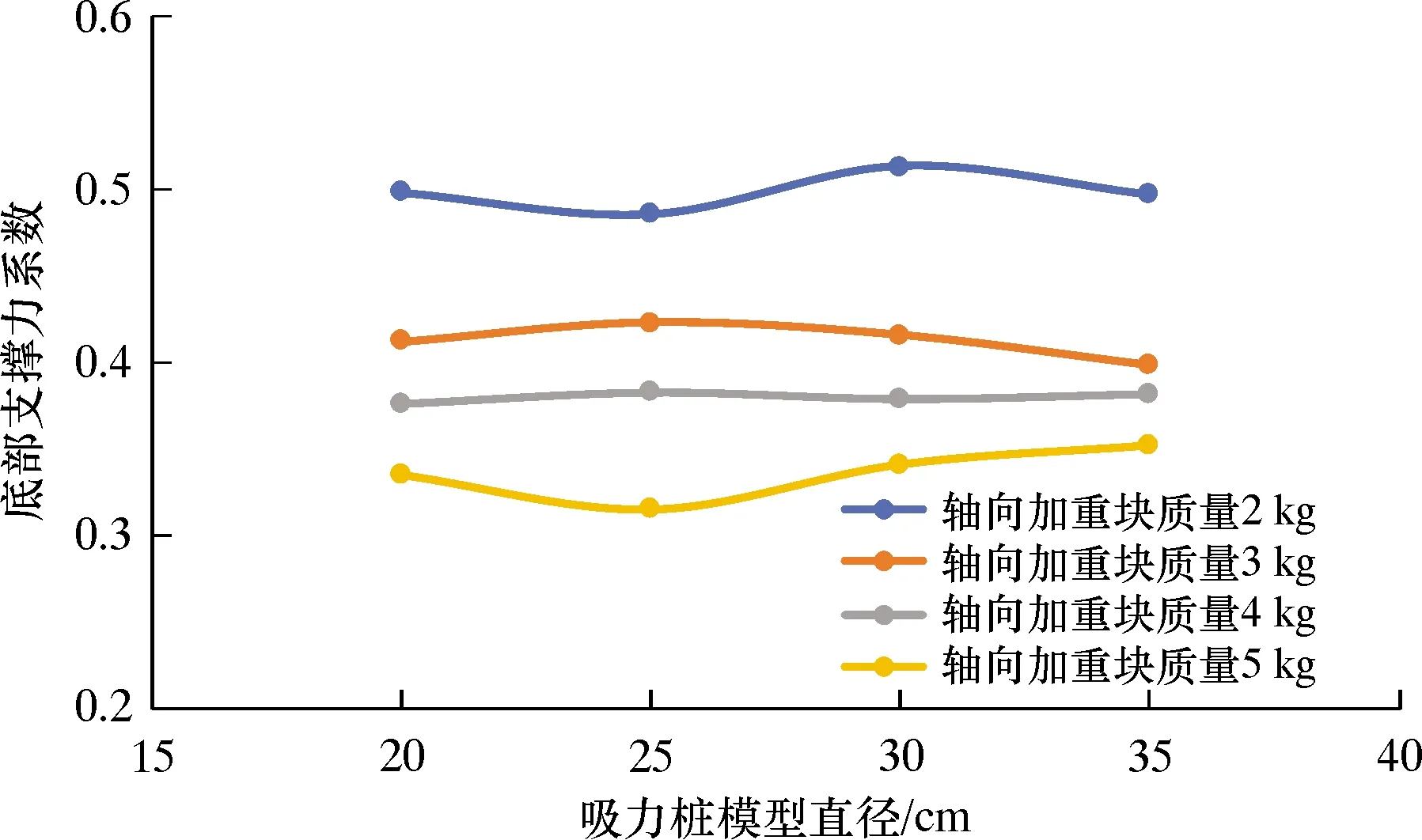
图17 底部支撑力系数随吸力桩模型直径的变化关系

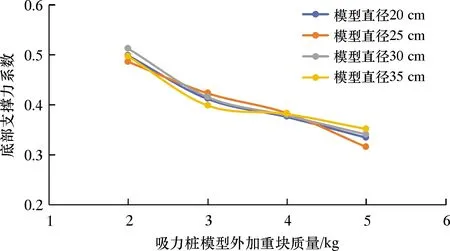
图18 底部支撑力系数随吸力桩模型外加重块质量的变化关系

由图17可见，相同加重块质量条件下吸力桩模型的底部支撑力系数不受吸力桩直径影响，且在相同吸力桩模型尺寸条件下，随着加重块质量的增加，底部支撑力系数降低。从图18可见，对于不同直径的吸力桩模型，底部支撑力系数随加重块质量的增加呈相同的下降趋势。试验结果说明，得出的底部支撑力系数具有统一的变化关系，求解β方法的假设满足要求。

5 结 论

(1)通过理论方法对模拟试验进行计算，吸力桩建井的承载力由侧向摩阻力和底部支撑力共同承担，且底部支撑力与侧向摩阻力的比值与吸力桩直径有关。

(2)侧向摩阻力系数和底部支撑力系数几乎不受吸力桩尺寸的影响，但受到外加载荷的影响较大，体现在下入深度不同时，随着外加载荷增加，吸力桩模型下入深度增加，侧向摩阻力系数先增加后减少，底部支撑力系数降低。由于下入深度增加，底部支撑力占承载比例减小，所以计算得到的比例系数降低。

(3)本文提出的在重力沉贯进行过程确定的承载力系数的取值范围仅适用于试验模型尺寸及渤海浅层黏性土土层条件，承载力系数估算方法可以用于指导吸力桩建井施工以及后续的承载力计算。