邮轮支柱板架连接点极限承载力研究

余建星，袁祺伟，葛珅玮，余 杨，王华昆，周 文，陈佰川

（1.天津大学水利工程仿真与安全国家重点实验室，天津 300072；2.天津大学天津市港口与海洋工程重点实验室，天津 300072；3.招商局邮轮制造有限公司,江苏南通 226100；4.北部湾大学机械与船舶海洋工程学院，广西钦州 535011）

0 引 言

随着邮轮产业的发展，我国对邮轮自主设计建造的需求日益迫切。由于功能和服务需求，邮轮上存在大量的异型结构。如邮轮的客房集中区域，巨大的购物中心和影院，这些场所的特殊功能需求导致不能采取较密集的横舱壁来支撑甲板板架，因此在这些设施位置，甲板板架跨距较大[1]。甲板板架与支柱连接位置的受力较常规船型的板架受力更复杂，需要对其进行极限承载力的研究以确保可靠性。

国内外的研究主要关注常规船型的板架极限承载力，且区别大部分在于有限元模型的建模范围、建模方法以及模型的边界条件。2009 年，Paik 等[2]研究了加筋板的极限承载力，模型横向范围选取整个船宽，与纵向平行的板边采取了简支约束。纵向建模范围为1/2+1+1/2 强构件跨度，与横向平行的板边采用对称约束。建模时将强构件简化为约束，不进行强构件建模。2011 年，万琪等[3]研究了大跨度甲板的纵向稳定性，比较了3 种建模方式，即整个模型采用梁单元，只将纵骨简化为梁单元和将强横梁也简化为梁单元对极限承载力的影响。2013 年，Xu 等[4]将加筋板的有限元模拟和试验进行了比较，分别采用简支边界条件、对称边界条件和简支对称混合边界，利用couping 进行耦合实行位移加载，并对比了3种简化模型的边界条件加载的结果。2013年，张婧等[5]考虑了3种不同的模型范围选取对板架极限承载力的影响，以及不同的初始缺陷对极限承载力的影响，最后考虑了复杂加载的情况。2014年，Shanmugam等[6]对加筋板进行了试验和有限元分析，有限元建模完整地模拟了整个实验，没有对模型做任何简化。板边简支约束，加载为面内轴向压缩载荷和垂直于板架的压力混合加载。2014年，Satoyuki Tanaka 等[7]研究了板架的极限承载力并与数值计算公式进行对比，指出不同建模范围有不同边界条件，1/2+1/2强构件跨度的模型为简支边界条件，而1/2+1+1/2强构件跨度的模型为对称边界条件。2018 年，Yang 等[8]研究了动力作用下的加筋板的极限强度。采用动态加载下的材料本构关系，其模型范围是横向和纵向均为1/2+1+1/2强构件跨度，将横向纵向强构件简化为模型的边界条件，边界条件介于简支和固支之间。

综上，目前主要的研究方向为常规船型的常规板架以及大跨度单层板架和双层板架在各种载荷工况下的极限承载力，并没有考虑到支柱与大跨度甲板连接位置的受力复杂性而导致该结构可能的破坏。本文利用ABAQUS 建立邮轮支柱甲板连接位置的有限元模型，通过计算得到支柱受压力作用下板架屈曲的极限承载力，并进行参数敏感性分析。

1 有限元模型

1.1 模型参数

邮轮支柱甲板结构如图1所示，支柱、纵骨及纵桁和强横梁截面图如图2所示。对应的尺寸如表1所示[1]，其中支柱壁厚根据中国船级社规范[9]获得，当船长L＞150 m 时，支柱最小壁厚为7 mm，取最小壁厚7 mm。根据中国船级社规范[9]支柱剖面积计算公式，邮轮的支柱半径根据以上数据取200 mm。根据Shi等[10]的论文中的邮轮中剖面图，各层甲板间高度在2800～6180 mm之间，选定支柱长度为3000 mm。

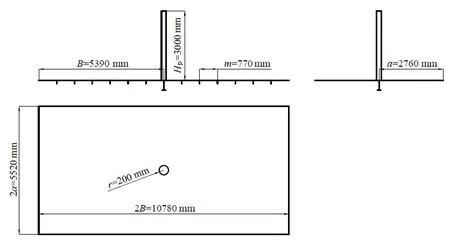
图1 邮轮支柱甲板结构示意图Fig.1 Pillar and deck structure of cruise

由于支柱布置在强纵桁和强横梁相交处，因此模型范围为支柱前后左右各一个强构件间距。整个模型采用壳单元。为简化计算，建模时只建立了球扁钢形式的腹板结构，忽略了球头的尺寸，简化后的纵骨截面尺寸如图2（b）所示。

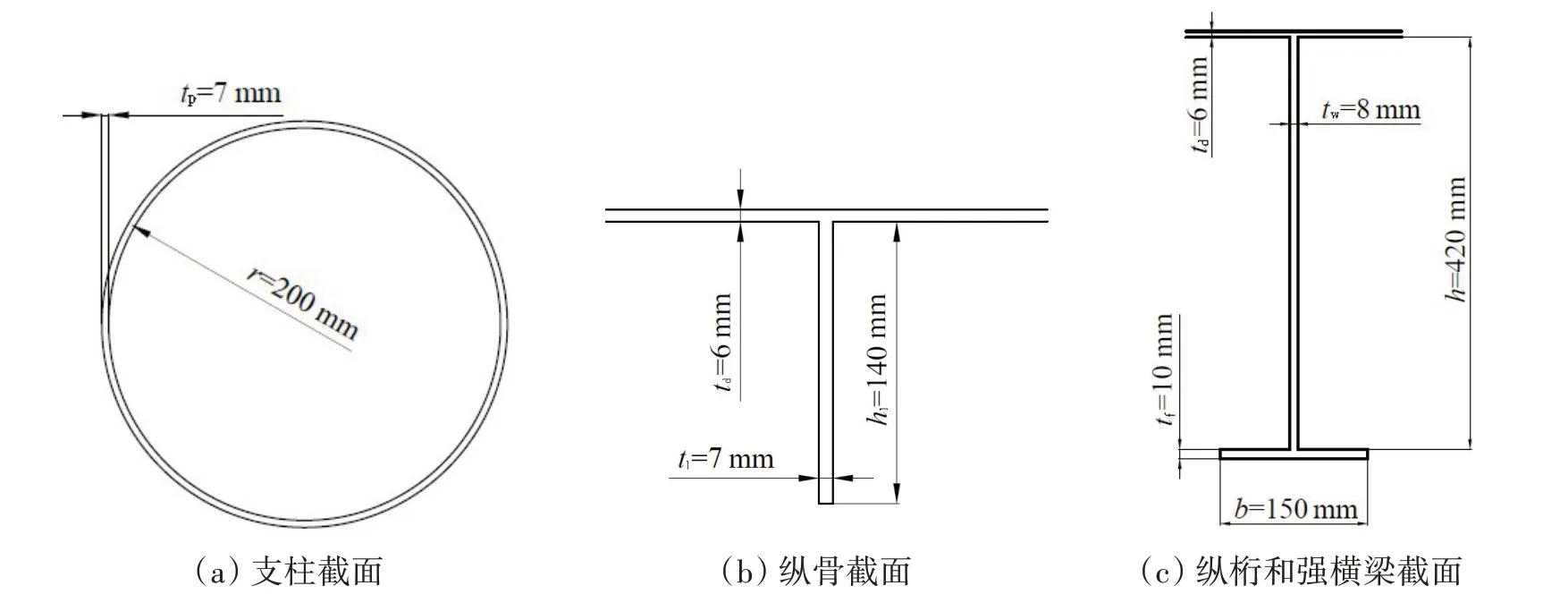
图2 截面示意图Fig.2 Diagram of beam section

根据Shi 等[10]的论文，邮轮的材料分为Q235 钢和Q355钢。本文模型的材料均为Q235钢，材料的应力应变曲线采用双线性模型[10]，如图3 所示。对应的材料参数如表1所示。

表1 邮轮材料数据Tab.1 Material properties of cruise

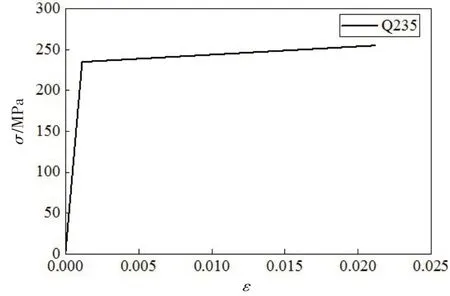
图3 应力应变曲线Fig.3 Stress-strain curve

1.2 载荷及边界条件

采用ABAQUS有限元软件模拟邮轮支柱板架连接位置在承受支柱压力载荷后板架受面内压缩载荷而可能发生的破坏，分为两个分析步：

第一步为支柱上部结构通过支柱施加传递压力，忽略了结构自身重力产生的变形。采用静力分析步得到板架受到支柱压载后的应力及变形。

第二步为板架面内施加的压缩载荷。设置参考点并耦合板边位移，以位移方式进行加载，采用静力分析步计算得到板架的极限承载力。

根据Yu 等[11]的论文，与强构件相交的纵骨、纵桁和横梁的边界条件为除加载方向位移外的所有自由度约束。根据Kim 等[12]的论文，在模型中心点施加两方向位移约束可以很好地模拟四个板边同时加载的情况。因此在模型的初始状态：AB板边节点除A、B两点耦合U2、U3、UR2、UR3 四个自由度到板边中点位置的参考点RP1。MN板边节点除M、N两点耦合U2、U3、UR2、UR3 四个自由度到板边中点位置的参考点RP2。AM板边节点除A、M两点耦合U1、U2、UR1、UR2四个自由度到板边中点位置的参考点RP3。BN板边节点除B、N两点耦合U1、U2、UR1、UR2四个自由度到板边中点位置的参考点RP4。支柱最上端节点耦合所有自由度到圆心位置的参考点RP5。

在第一个分析步中，通过设置参考点RP5 的y方向作用力施加支柱载荷。由于板架的A、B、M、N四节点为板架横边与纵边的公共节点，因此约束六个自由度。RP1、RP2 限制耦合的U2、U3、UR2、UR3 四个自由度；RP3、RP4 限制耦合的U1、U2、UR2、UR3 四个自由度。纵骨和强纵桁限制U2、U3、UR1、UR2、UR3的自由度；强横梁限制U1、U2、UR1、UR2、UR3的自由度。

在第二个分析步中，板的纵向中线和横向中线的交点O限制U1、U3 两个自由度；A、B、M、N四点设置U1、U3 位移进行加载；RP1、RP2 设置U3 位移进行加载；RP3、RP4设置U1 位移进行加载；纵骨与强纵桁设置U3 位移进行加载；强横梁设置U1 位移进行加载。具体有限元模型与建模坐标系如图4所示。

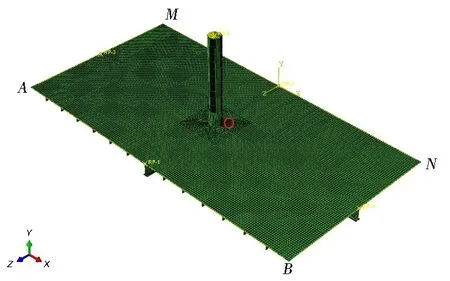
图4 支柱甲板连接位置计算模型Fig.4 Calculation model of pillar deck conncction position

1.3 初始变形缺陷设置

在焊接过程中板架会不可避免地产生初始变形缺陷，而缺陷的存在会影响连接位置板架的极限承载力。板架的初始缺陷分为三种[13]：板架的整体缺陷woc，骨材之间板格的缺陷wopl以及骨材的缺陷wos，板架缺陷如图5所示。

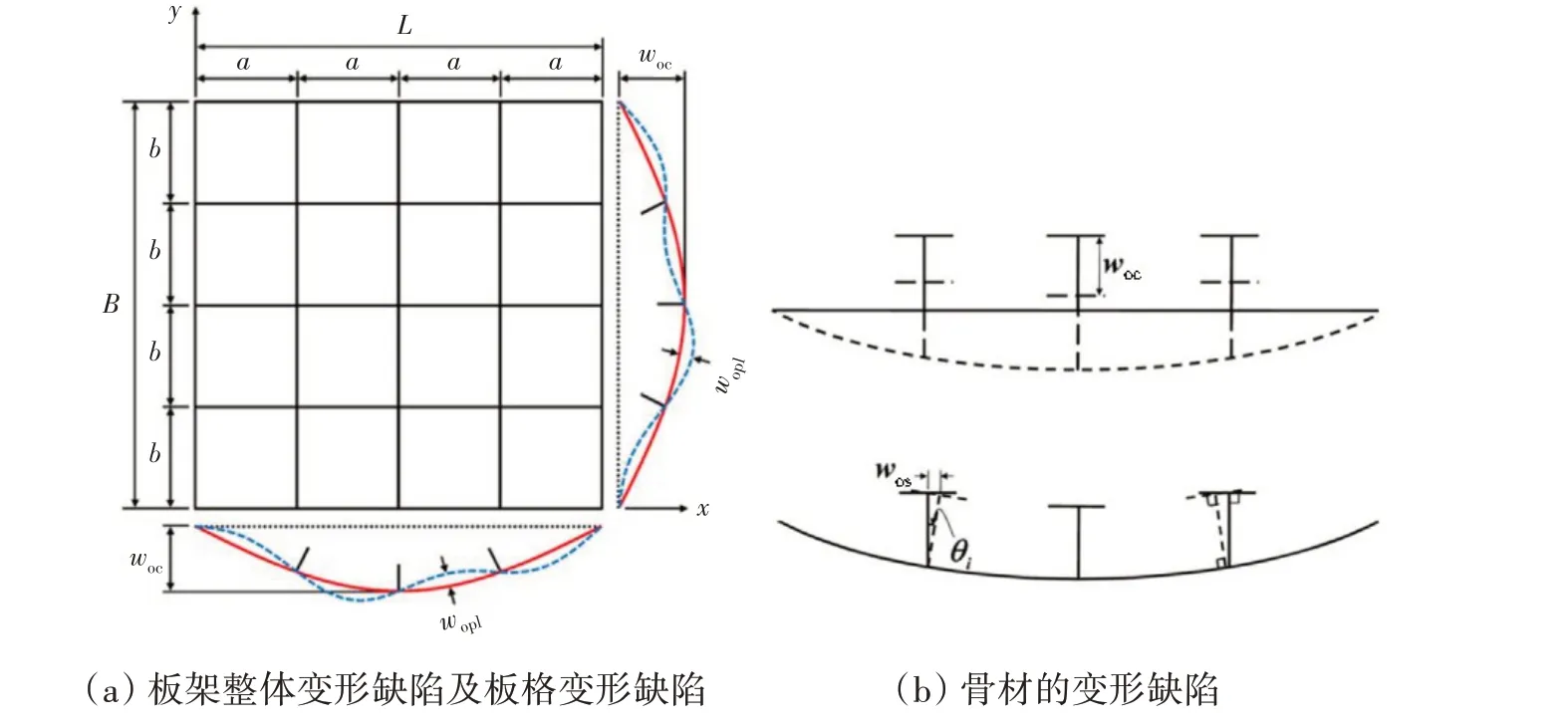
图5 变形缺陷示意图Fig.5 Diagram of deformation defect

初始变形缺陷的设置分为三步：首先获得无缺陷结构模型的所有节点坐标，根据节点坐标对节点所在区域进行分类；之后计算不同区域上节点偏移原坐标的长度，获得有缺陷结构模型的所有节点坐标；最后修改ABAQUS 计算输入文件在model 中导入有缺陷的结构模型。偏移原坐标的长度由式（1）～（6）计算[13-14]。

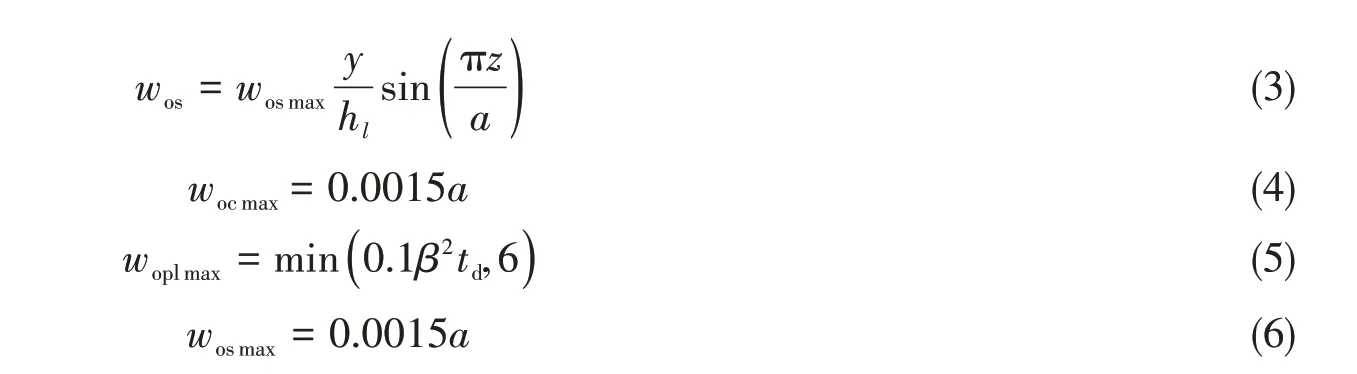
式中各个参数已在表1中列出，W为支柱板架半宽（5390 mm），β为纵骨间板格的柔度系数，根据式（7）计算。

式中，x、y、z为图3中板架模型的节点坐标。

1.4 模型边界条件验证

以本文在面内压缩载荷情况下板边和纵骨的边界条件，对已发表的板架面内压缩试验和有限元模拟，建立强结构间的加筋板模型并计算极限承载力，结果如表2所示。

表2 板架模型验证Tab.2 Validation of frame model

通过对比发现，采用本文在纵桁和强横梁位置的边界条件可以较好地模拟加筋板的极限承载力，误差在5%左右，因此本文数值模型是可靠的。

2 结果分析

基于上述验证后的数值模型，研究了1×105～7×105N 范围内的支柱载荷作用下不同板架面内加载模式对极限承载力的影响。之后对支柱板架连接位置的结构参数：支柱半径r、支柱厚度tp、纵桁和强横梁腹板高度h、纵桁和强横梁腹板厚度tw、纵桁和强横梁翼板宽度b、纵桁和强横梁翼板厚度tf进行了敏感性分析。采用σx/σY、σy/σY、σz/σY应力比的形式来表征所受载荷的大小，其中σx为板架纵向受到的应力，σy为板架横向受到的应力，σz为支柱受到的垂直于板面的应力。由于壁厚相对半径较小，因此采用式（8）计算σz，式中F为支柱受力。

2.1 不同的面内载荷的影响

由于本文板架面内压缩载荷是通过设置板边位移进行施加的，因此不同的纵向及横向压缩载荷是通过设置不同比例的纵向及横向板边位移来实现。考虑的8种面内压缩工况如表3所示。

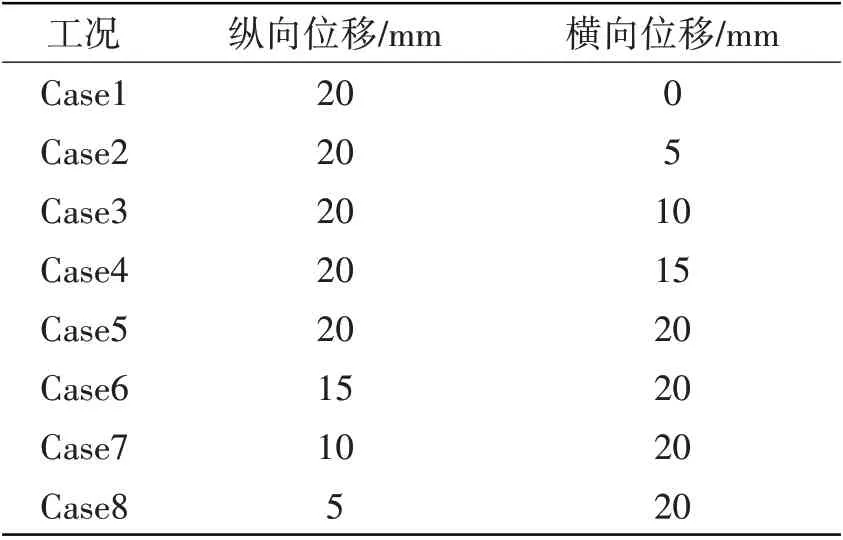
表3 8种面内压缩工况Tab.3 Eight in-plane compression conditions

Case6加载模式中由于板架在支柱受3×105N的压力情况下，随着位移增加，横向应力峰值早于纵向应力峰值出现，因此板架开始从纵向破坏转变为横向破坏。对比Case3 和Case7 加载模式下支柱受1×105N 压力作用后板格的临界屈曲状态，从图6 中发现，板格纵向与横向屈曲破坏相比，板格纵向屈曲破坏在临界屈曲时存在较明显的纵向条纹状的材料屈服区域，而横向破坏则为块状材料屈服区域。

图6 两种不同破坏模式的临界屈曲状态（放大10倍）Fig.6 Critical buckling state of two different failure modes(magnified 10 times)

在支柱受压情况下，不同面内加载模式作用下板架的极限承载力如图7所示。从图中可以看出，无论是板架纵向破坏还是横向破坏，随着支柱受载增加，板架的极限承载力下降。且随着板架面内横向应力的增加，板架纵向破坏时的极限承载力降低，反之亦然。

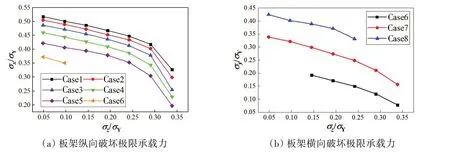
图7 不同加载模式对极限承载力的影响Fig.7 Influence of different loading modes on ultimate bearing capacity

从图7（a)中发现，当σz/σY＜0.3 时，极限承载力下降较缓，因为主要的失效模式为板格屈曲破坏。当σz/σY＞0.3时，极限承载力的降幅增大，这是由于支柱受压增大导致板架中心垂向变形较大，失效模式从板格屈曲破坏转变为板架梁的弯曲破坏，如图8所示。

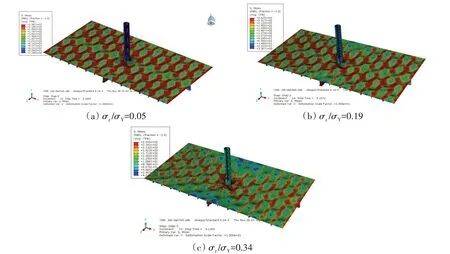
图8 Case1位移加载模式下支柱受载后的临界失效模式（放大10倍）Fig.8 Critical failure mode of pillar loaded in Case1 loading mode(magnified 10 times)

综合板架纵向极限承载力和横向极限承载力，最终得到板架在支柱压力作用下的临界屈曲应力曲线，如图9所示。该临界曲线可以根据板架面内所受应力确定板架是否发生破坏。如果坐标落在曲线的右上方，则表示在该加载模式下，板架发生了破坏，坐标落在左下方则表示板架并未发生破坏。

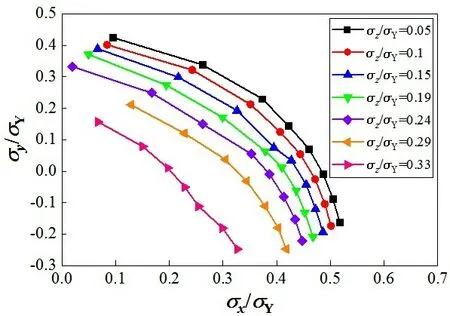
图9 板架受支柱压力作用后的临界屈曲应力曲线Fig.9 Critical buckling failure curve of the stiffened plate subjected to pillar pressure

2.2 支柱半径的影响

在之后的参数敏感性分析中，只考虑了Case3 和Case7 这两种位移加载模式下参数对极限承载力的影响，因为在这两种位移加载模式下，板架是完全的纵向破坏和横向破坏。计算了支柱半径（r）分别为100～400 mm时两种加载模式下的极限承载力，如图10所示。

从图10可以看出，无论是纵向破坏还是横向破坏，当支柱受压力较小时，半径不同对板架的极限承载力影响较小，因为最开始的失效模式为板架屈曲破坏。而随着支柱半径增加，支柱受载增加较快，失效模式从板格屈曲转变为板架梁整体弯曲也较快，极限承载力下降较快。

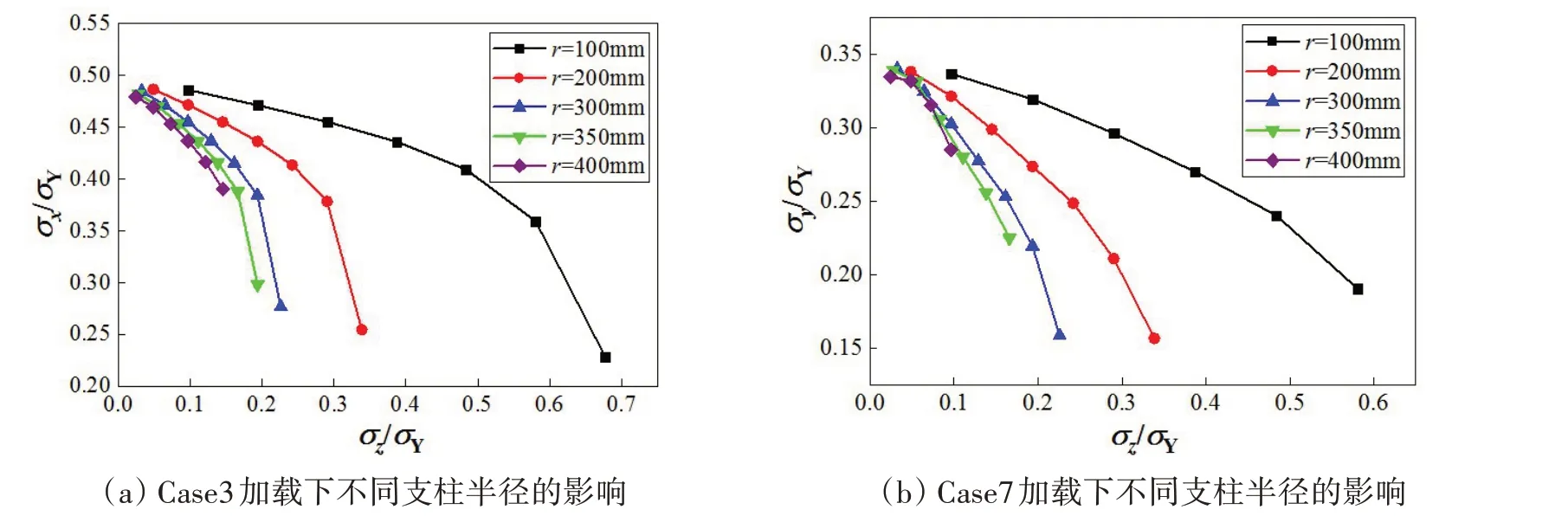
图10 不同支柱半径对极限承载力的影响Fig.10 Influence of different pillar radii on ultimate bearing capacity

2.3 支柱壁厚的影响

计算了支柱壁厚tp分别为7～15 mm 时两种加载模式下板架的极限承载力，如图11 所示。从图中可以看出，无论是纵向破坏还是横向破坏，当支柱受压力较小时，壁厚不同对板架的极限承载力影响较小，而随着支柱壁厚增加，支柱受载增加，板架的极限承载力下降。

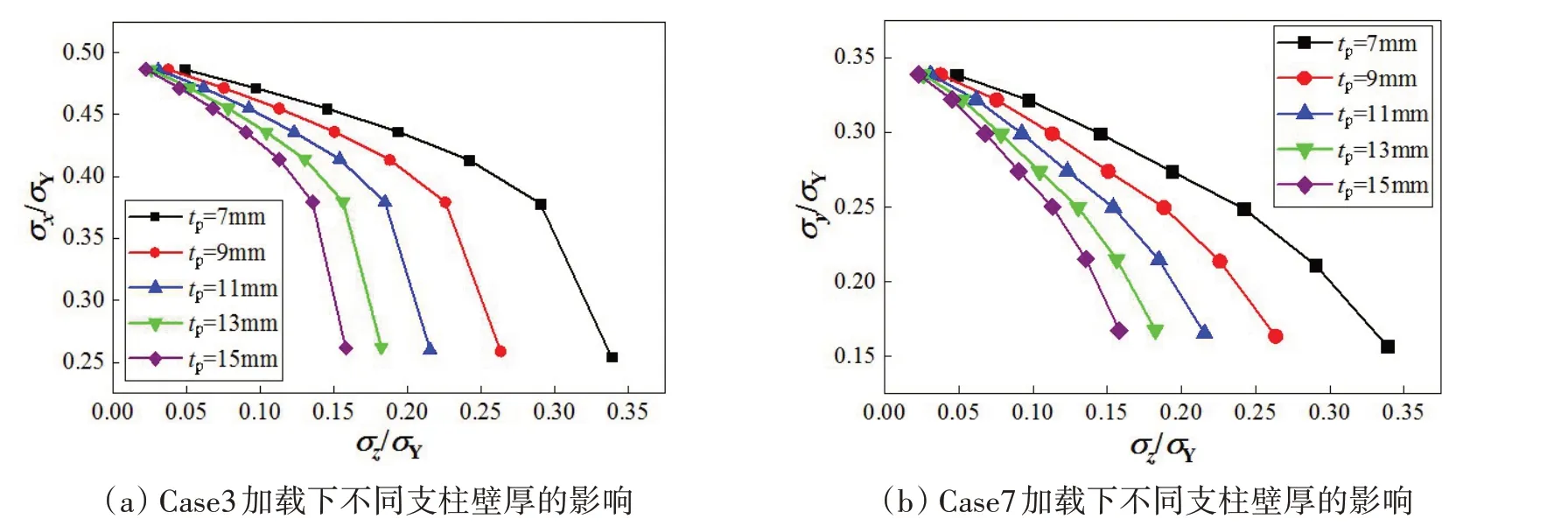
图11 不同支柱壁厚对极限承载力的影响Fig.11 Influence of different pillar thicknesses on ultimate bearing capacity

2.4 纵桁和强横梁腹板高度的影响

计算了纵桁和强横梁腹板高度h分别为280～560 mm情况下板架的极限承载力，如图12所示。从图中可以看出：不论是纵向破坏还是横向破坏，当支柱受载较小时，纵桁和强横梁腹板高度对极限承载力的影响较小。因为板架均为板格屈曲破坏，随着支柱受载增加，腹板高度越高，支柱作用下板架的变形越小，板架的极限承载力越大。但随着腹板高度增加，板架极限承载力的提高越来越有限。不同腹板高度的板架临界失效模式如图13所示。

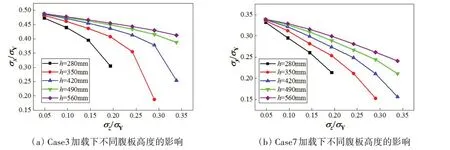
图12 不同腹板高度对极限承载力的影响Fig.12 Influence of different web thicknesses on ultimate bearing capacity

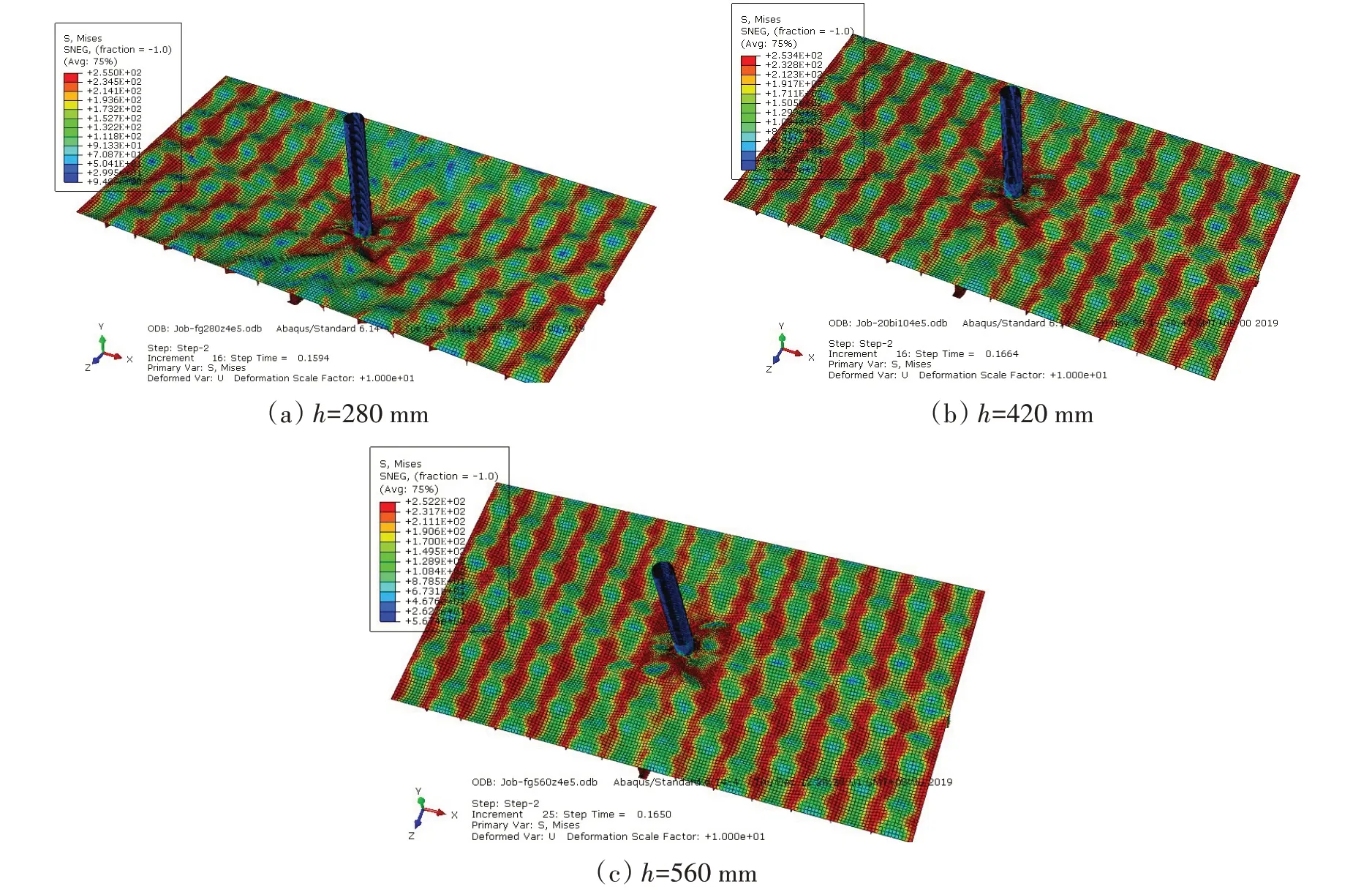
图13 Case3位移加载模式下支柱受4×105 N轴向压力后板架的临界失效模式（放大10倍）Fig.13 Critical failure mode after pillar is loaded with 4×105 N in Case3 loading mode(magnified 10 times)

2.5 纵桁和强横梁腹板厚度的影响

计算了纵桁和强横梁腹板厚度tw分别为4～12 mm 情况下的板架极限承载力，结果如图14 所示。从图14中可以看出：无论是纵向破坏还是横向破坏，当支柱受载较小，强构件腹板厚度对板架极限承载力几乎没有影响。而随着支柱载荷增加，腹板厚度越小，极限承载力发生突然下降的情况就越早。这是因为支柱受载较小时，失效模式为板格屈曲，强构件腹板厚度对板格屈曲影响不大，而支柱受载增大后，腹板厚度小的板架受支柱作用变形较大，失效模式转变为整个板架梁的弯曲，而强构件厚度小会导致整个板架抗弯能力低，就会出现极限承载力提前骤降的情况。可以看出，提高腹板厚度对板架极限承载力提高幅度不明显，但能明显提高极限承载力骤降时的支柱受力。

图14 不同腹板厚度对极限承载力的影响Fig.14 Influence of different web thicknesses on ultimate bearing capacity

2.6 纵桁和强横梁翼板宽度的影响

翼板宽度b分别为25～125 mm 情况下板架受支柱压载后的极限承载力如图15所示。从图中可以看出，无论纵向破坏还是横向破坏，其极限承载力变化与腹板厚度较为一致，支柱受载较小时，板架主要为板格屈曲破坏。翼板宽度影响不是很大，因此板架极限承载力非常接近。支柱受载增大后，翼板宽度小的板架变形大，板架失效模式先于翼板宽度大的板架转变为板架梁整体弯曲破坏，翼板宽度小的板架极限承载力先发生骤降。

图15 不同翼板宽度对极限承载力的影响Fig.15 Influence of different widths of wing on ultimate bearing capacity

从图16可以看出，不同翼板宽度在相同支柱加载下的不相同的失效模式。b=150 mm时板架的失效模式相较于b=100 mm的板架失效模式更接近板格屈曲。

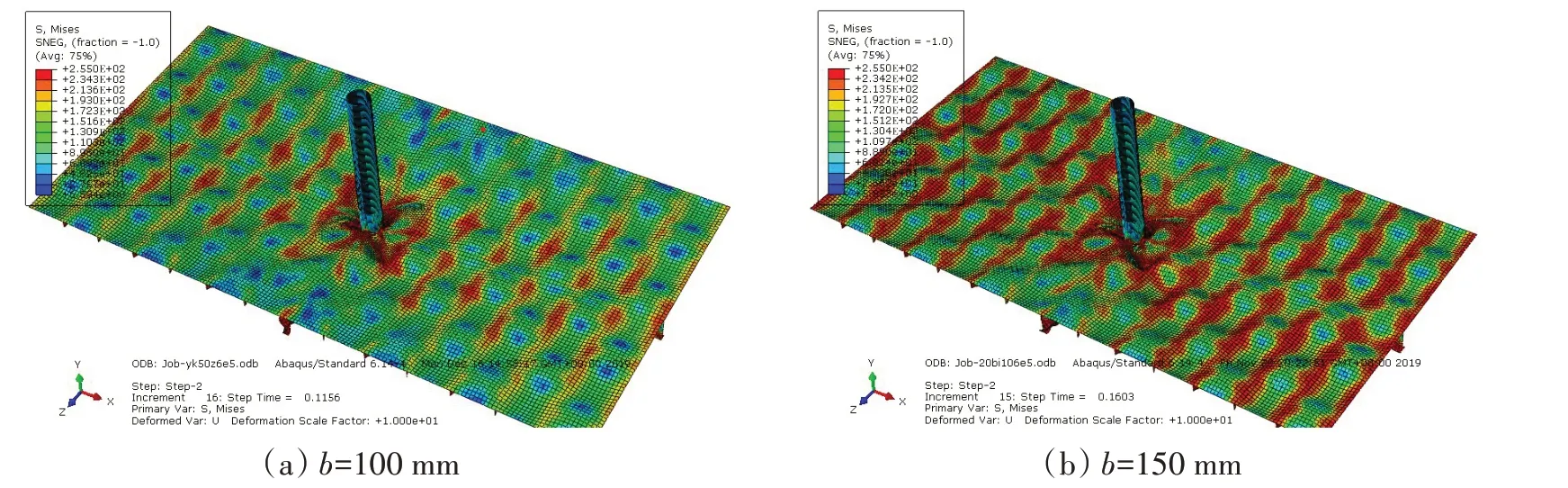
图16 支柱Case3加载6×105 N时的临界失效模式（放大10倍）Fig.16 Critical failure mode after pillar is loaded with 6×105 N in Case3 loading mode(magnified 10 times)

2.7 纵桁和强横梁翼板厚度的影响

翼板厚度tf分别为6～14 mm 情况下板架受支柱压载后的极限承载力如图17所示。从图中可以看出，无论是纵向破坏还是横向破坏，支柱受载较小时，不同腹板厚度的板架极限承载力差距不大。随着支柱受载增加，腹板厚度小的板架极限承载力较小。纵向破坏时腹板厚度小的板架极限承载力骤降先发生，而横向破坏时极限承载力并没有特别明显的骤降。

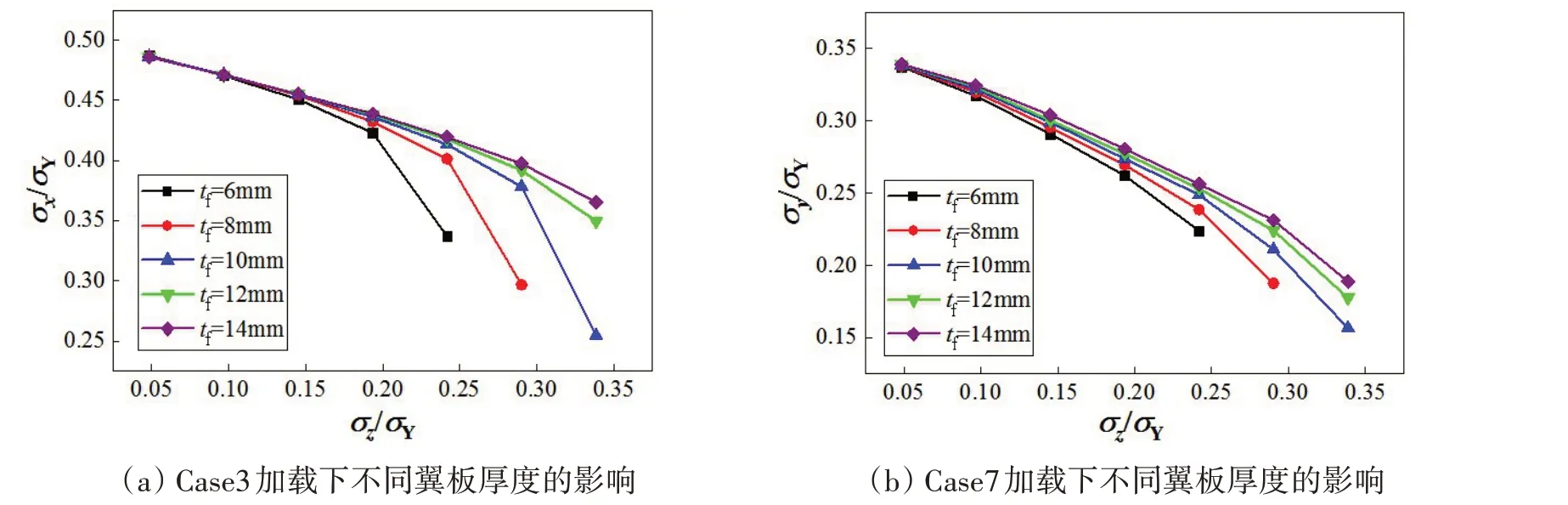
图17 不同翼板厚度对极限承载力的影响Fig.17 Influence of different thicknesses of airfoil on ultimate bearing capacity

3 结 论

本文通过修改ABAQUS 计算输入文件建立含焊接缺陷的邮轮支柱板架连接位置的有限元模型，利用ABAQUS计算了支柱承载情况下受面内压缩载荷板架的极限承载力，并对支柱、纵桁和强横梁的结构参数进行了敏感性分析，得出以下结论：

（1）随着支柱单位面积受载的增加，板架的极限承载力降低。且一旦支柱受载较大后，板架的失效模式从板格屈曲转变为整个板架梁的弯曲破坏。

（2）板架纵向破坏时，横向面内压缩应力增加，板架极限承载力降低。板架横向破坏时，纵向面内压缩应力增加，板架极限承载力降低。

（3）随着支柱单位面积受载增加，支柱半径大的板架极限承载力越小，支柱厚度越大的板架极限承载力越小。

（4）随着支柱单位面积受载增加，纵桁和强横梁腹板高度越小的板架极限承载力越小。纵桁和强横梁腹板厚度越小的板架极限承载力越小。

（5）随着支柱单位面积受载增加，纵桁和强横梁翼板宽度越小的板架极限承载力越小。纵桁和强横梁翼板厚度越小的板架极限承载力越小。