正常连接与悬挂撤离工况下深水钻井隔水管动力特性与安全分析

毛良杰，付燈煌，曾 松

（西南石油大学a.油气藏地质及开发工程国家重点实验室；b.石油与天然气工程学院，成都 610500）

0 引 言

世界海洋油气资源储量丰富，海洋油气资源量约占油气资源总量的34%，探明率仅30%左右，具有巨大发展潜力[1-2]。隔水管是连接钻井平台与水下井口的通道，同时也是十分薄弱的部分。正常作业时，隔水管会受到风、浪、流等海洋环境载荷的影响；当台风等极端天气来临时，隔水管必须从底部隔水管总成（LMRP）处断开进行悬挂撤离。海洋环境载荷、平台漂移、悬挂模式等都会影响隔水管的安全。当隔水管应力超过屈服应力或者接头转角超过极限时，可能出现隔水管断裂、碰撞月池等事故。因此，对正常连接工况以及悬挂撤离工况下深水钻井隔水管进行安全分析对保障隔水管安全有着重要意义。

许多学者对隔水管进行了研究，频谱法[3]、有限差分法[4]、时域分析与频域分析法[5-7]和有限单元法[8-11]等都被用来分析隔水管受力及变形等特征。进一步地，许多学者分析了隔水管动力学特性[7-8，10-12]，指出深水钻井隔水管横向位移与弯矩等主要受张顶力、海流流速和隔水管壁厚等因素的影响。不少学者研究了不同环境载荷及作业工况下隔水管的安全。李子丰等[13]采用有限差分法对隔水管在外载荷作用下的横向位移、转角等进行了分析，指出深水隔水管最大转角出现在顶部。郭海燕等[14]建立了考虑隔水管内部流体流速以及外部海流耦合作用的隔水管运动模型，指出内流流速增大会降低隔水管自振频率。畅元江等[15]分析总结了水深、海流、正常与悬挂工况对超深水钻井隔水管设计的影响，研究表明水深和海流对隔水管设计影响较大。孙友义[16]研究了正常连接与悬挂隔水管强度评价方法，提出了基于风险增强的疲劳准则进行隔水管VIV 疲劳安全评估方法。针对悬挂隔水管，齐娟娟[17]和Liu 等[18]研究了软悬挂与硬悬挂状态隔水管的受力与变形，指出可以通过布置浮力块和减小平台运动速度等方式来减小隔水管位移及弯矩；盛磊祥等[19]、陈黎明等[20]和许亮斌等[21]研究了悬挂长度对悬挂隔水管撤离安全窗口的影响，认为应当在悬挂撤离前回收部分隔水管；同时，他们都认为隔水管悬挂撤离时软悬挂模式更为安全可靠。Wang 等[22-24]等还研究了隔水管安装作业操作窗口，指出小波高和长周期的波浪载荷环境更适合隔水管安装作业。

目前国内外研究主要分别对不同工况下隔水管变形、位移及其影响因素进行分析，缺乏考虑实际配置全面地对隔水管进行安全分析研究，对不同海况与作业工况下的隔水管强度安全极限分析不足。本文建立了适合正常连接工况与悬挂撤离工况的隔水管动力分析模型，通过边界条件区分正常连接工况与悬挂撤离工况，并开展实验对模型正确性进行了验证。以中国南海深水井为实例，对正常连接与悬挂撤离工况下隔水管动力特性进行分析，并对不同海况、工况下隔水管的漂移限制及应力安全进行校核与讨论，可以为隔水管的安全作业提供指导。

1 隔水管动力模型建立

深水钻井隔水管可分为正常连接与悬挂撤离工况。正常连接工况示意图如图1 所示，隔水管顶端与可旋转挠性接头和伸缩节筒连接，底端采用可旋转挠性接头连接。紧急情况下，隔水管从LMRP与防喷器（BOP）连接处断开随平台进行悬挂撤离即为悬挂撤离工况。根据不同顶端连接方式，悬挂撤离又分为硬悬挂模式与软悬挂模式。软悬挂模式如图2（a）所示，隔水管顶部与正常钻井工况一样采用可旋转接头与伸缩筒连接于平台，而硬悬挂时隔水管与平台采用刚性连接，如图2（b）所示。

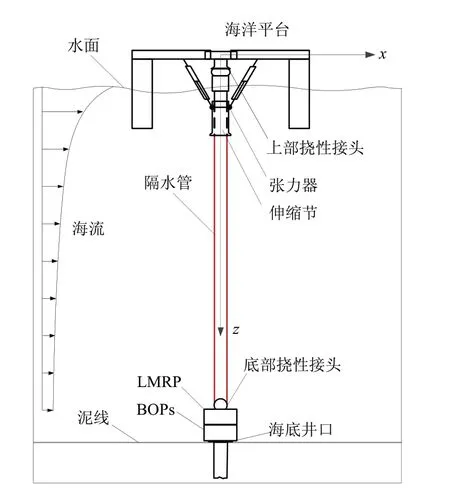
图1 正常钻井隔水管示意图Fig.1 Schematic for drilling riser under normal drilling condition

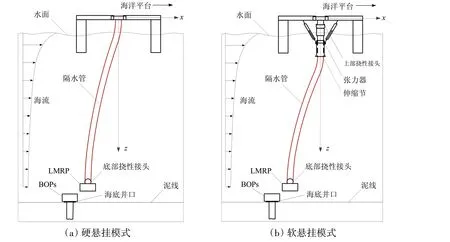
图2 悬挂撤离隔水管示意图Fig.2 Schematic for drilling riser under hang-off condition

1.1 隔水管模型控制方程

假设隔水管为连续体，视为长度远大于直径的细长梁，其控制方程可表示为[10-11]

式中，Ttop为顶部轴向预张力，N。

悬挂隔水管底部与BOP 断开后，只有LMRP 悬挂在隔水管底端。因此悬挂撤离模式下，隔水管轴向张力包括自身重力以及底部LMRP重力。

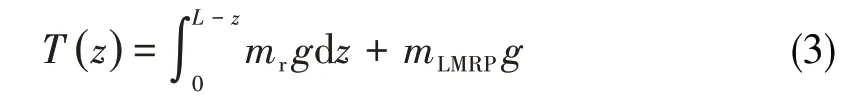
式中：L为隔水管长度，m；mLMRP为底部隔水管总成质量，kg。

1.2 边界条件

正常连接工况下，隔水管上端与平台采用挠性接头和伸缩节连接，顶端挠性接头旋转刚度为Ku，隔水管顶端速度等于平台运动速度。隔水管底端与BOP采用挠性接头连接，旋转刚度为Kd，并且底端为固定端，如图3（a）所示。因此，正常连接工况下隔水管上下端边界条件可以表示为

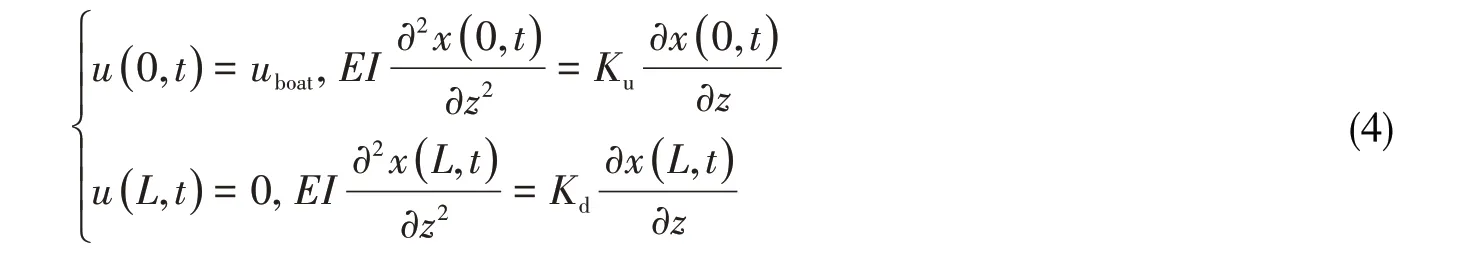
悬挂隔水管采用软悬挂模式连接时，顶部连接方式与正常连接工况相同，可随着平台移动而移动，而底部则为完全自由端，如图3（b）所示，因此边界条件可以写为

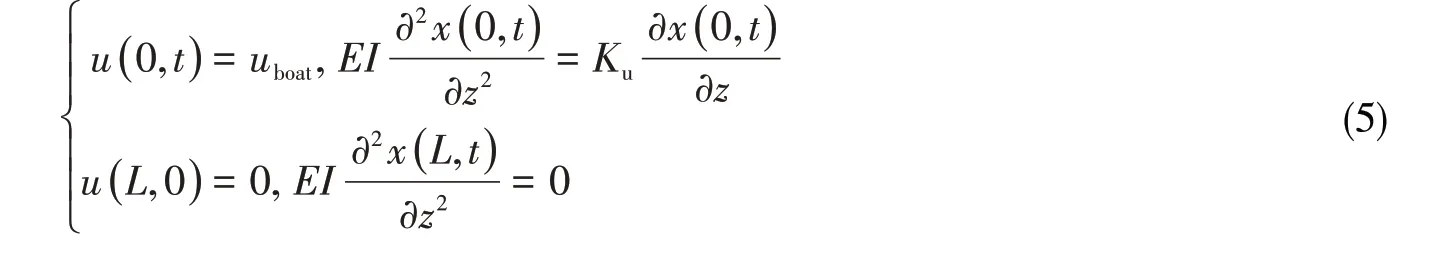
采用硬悬挂模式连接时，隔水管顶端与平台采用刚性连接，视为固定端，顶端转角为0°，而底部则为自由端，如图3（c）所示，因此边界条件可以写为

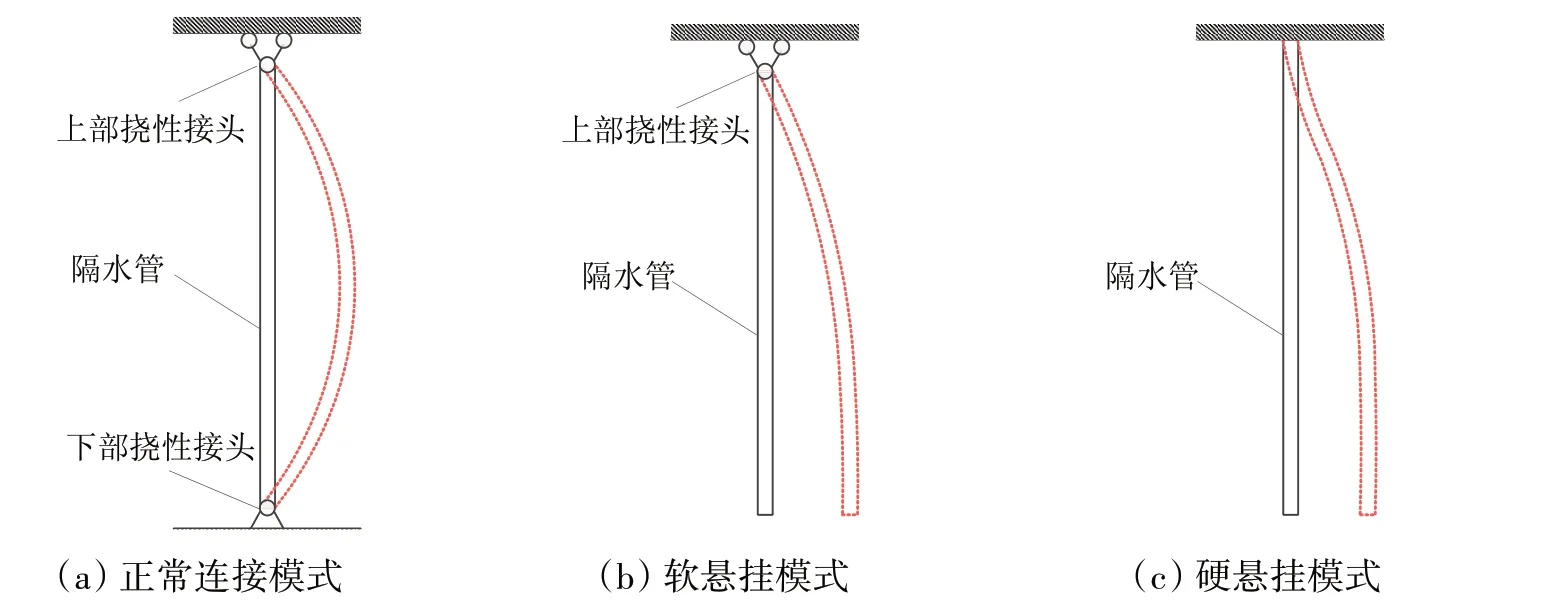
图3 边界条件示意图Fig.3 Schematic of boundary conditions

1.3 Von Mises应力

Von Mises应力是管柱设计、安全校核的主要准则，可以通过式（7）进行计算：

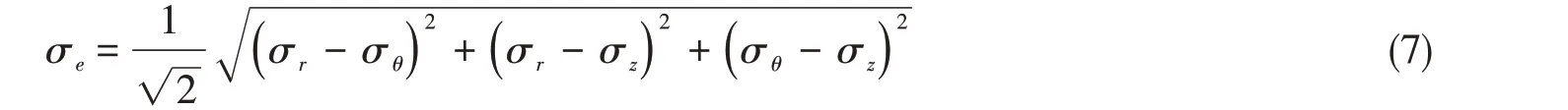
式中，σr、σθ、σz为三主应力，分别为径向、周向和轴向应力。通过下式计算：

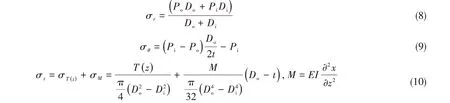
式中：Po、Pi分别为隔水管内、外静液柱压力，Do、Di分别为隔水管内、外直径，t为隔水管壁厚。

2 海洋环境载荷计算

隔水管位于海水环境中，在海洋环境载荷作用下发生变形。由于波浪力对隔水管变形的影响很小[11]，模型载荷主要考虑海水质点与管柱同时随时间动态变化下的海流力作用。隔水管可以看作细长梁，因此海洋环境载荷可以通过Morison方程来计算[25]：

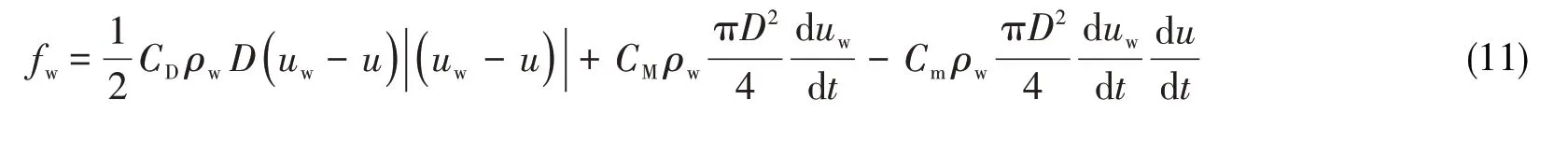
式中：CD为拖曳力系数，无量纲；ρw为海水密度，kg/m3；D为隔水管外径，m；uw为海流速度，m/s；u为隔水管横向运动速度，m/s；Cm为附加质量系数；CM为惯性力系数，等于Cm+1。

通常海流速度可以根据实际测量海水流速来获取，或者根据特定海域流速分布重现周期来获取海流流速分布剖面。模型假设海水流动方向为单一固定方向，实际撤离方向可能会与流体流动方向成一夹角α，如图4 所示，计算时以平台运动方向为参考，将流体速度折算到x轴方向。

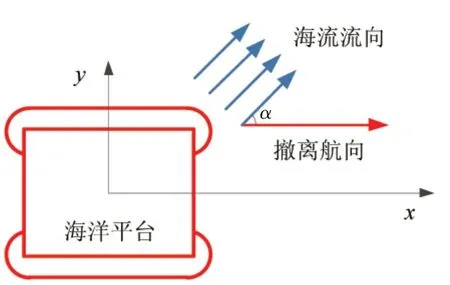
图4 撤离方向示意图Fig.4 Schematic of desired track of drilling platform

3 隔水管动力模型求解

模型采用有限单元方法求解，隔水管沿长度方向划分有限个微元段，微元段位移通过Hermite 插值方式表示。动力分析时间被划分为有限时间段，采用Newmarkβ迭代求解。

隔水管微元段受力状态如图5 所示，通过Hermite 方程，隔水管单元运动可以表示为[26]

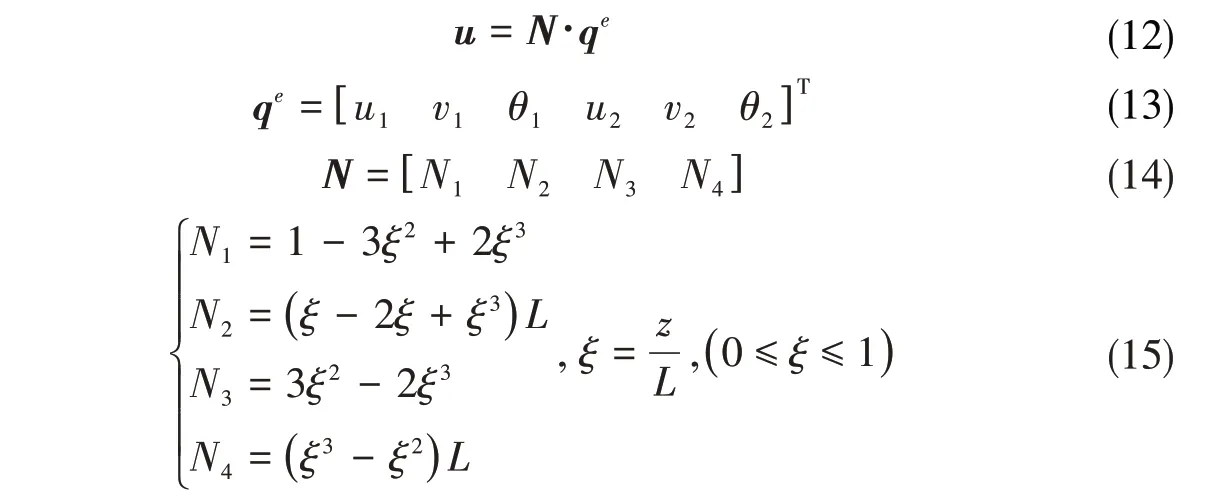
图5 隔水管单元受力分析Fig.5 Schematic for the force of one riser element

单元刚度矩阵Ke、单元质量矩阵Me、单元阻尼矩阵Ce以及单元载荷矩阵Pe可以通过式（16）求得：

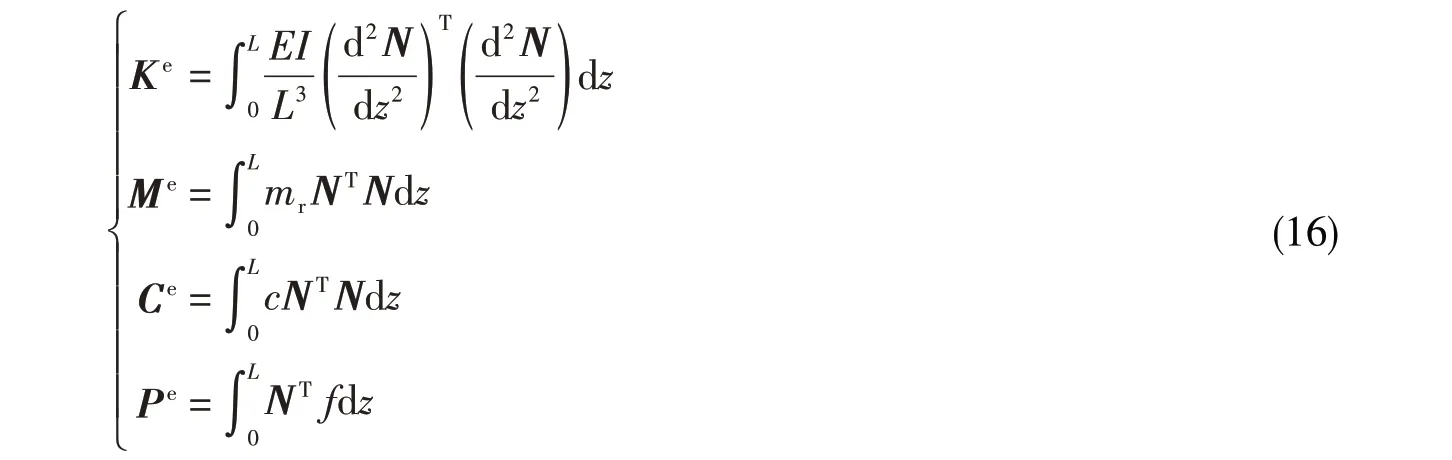
对整个隔水管坐标进行转换后，代入如下动力学运动方程[27]：

式中，u″为加速度，u'为速度，u为位移，f(t)为外力载荷矩阵。

方程（17）可通过Newmarkβ进行求解，详细求解步骤参见相关文献[11，27]。

4 隔水管动力模型验证

为了验证模型的正确性，设计了隔水管应力应变测试实验装置，如图6所示。实验装置包括隔水管测试模型、伺服电机及辅助导轨系统和应变监测分析系统。隔水管测试模型采用PVC管，上下两端采用可旋转的铰接接头连接，四周贴有光纤光栅传感器用于采集隔水管应变数据，通过数据处理可以获得隔水管变形参数[28]，光纤光栅传感器布置情况如图7 所示。实验时，通过上下两个伺服电机同步运动，拖动隔水管在水池中匀速运动，模拟均匀流作用下隔水管的变形。实验详细步骤、相似比尺效应设计及数据处理方法见文献[28-31]，实验隔水管模型特性及相关实验参数见表1[28-29]。

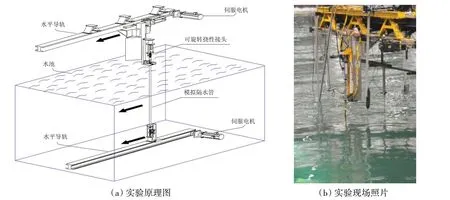
图6 实验装置示意图Fig.6 Schematic and picture of the experimental setup

图7 光纤光栅传感器布置情况Fig.7 Arrangement of the fiber Bragg grating sensors

表1 隔水管实验参数Tab.1 Main parameters in experiment model

进行对比验证时，数值模型采用实验模型参数进行计算，对比数值模型与实验隔水管的变形分布，对比结果如图8所示。可以看出，数值模型与实验的隔水管变形都在中部靠上的位置达到最大变形，并且隔水管变形的分布几乎一致，两者间微小的差异可能来自实验应变片及测试电线对管柱变形的影响。因此，该实验可以证明本文数值模型的正确性。

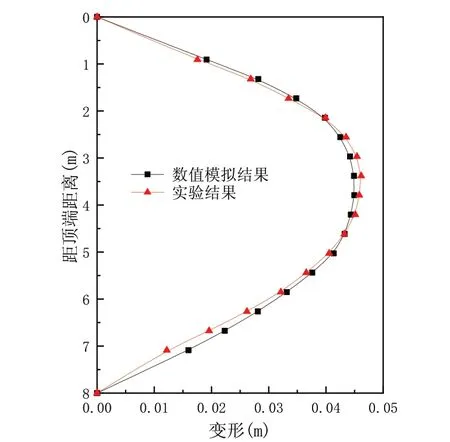
图8 数值模型与实验结果对比图Fig.8 Comparison between the numerical and experimental results

5 隔水管动力特性与安全分析

选取南海一深水井进行隔水管动力特性分析，主要参数见表2[11]。隔水管实际单根浮力块配置方案见表3，其中浮力块外径为1.3716 m，隔水管外径为0.5334 m，隔水管壁厚随浮力块配置变化。南海海流速度剖面及根据实际配置求得的初始载荷分布如图9[15，18]所示。针对正常连接工况以及悬挂撤离工况，通过分析隔水管应力分布及转角极限来研究隔水管的安全。隔水管最大可承受应力（屈服应力）为80 ksi（551.6 MPa），安全警戒应力为53.3 ksi（367.7 MPa）[32]，隔水管顶端转角极限为13.5°，底端转角极限为9°[33]。

表2 隔水管及南海特性参数Tab.2 Main parameters of the riser and hydrodynamic in South China Sea

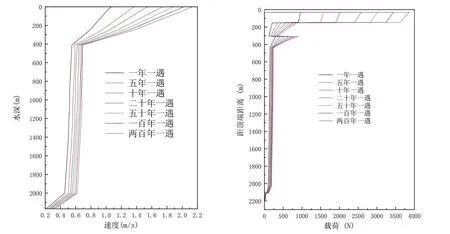
图9 海流流速分布及初始载荷分布Fig.9 Profile of the ocean current and the initial loads

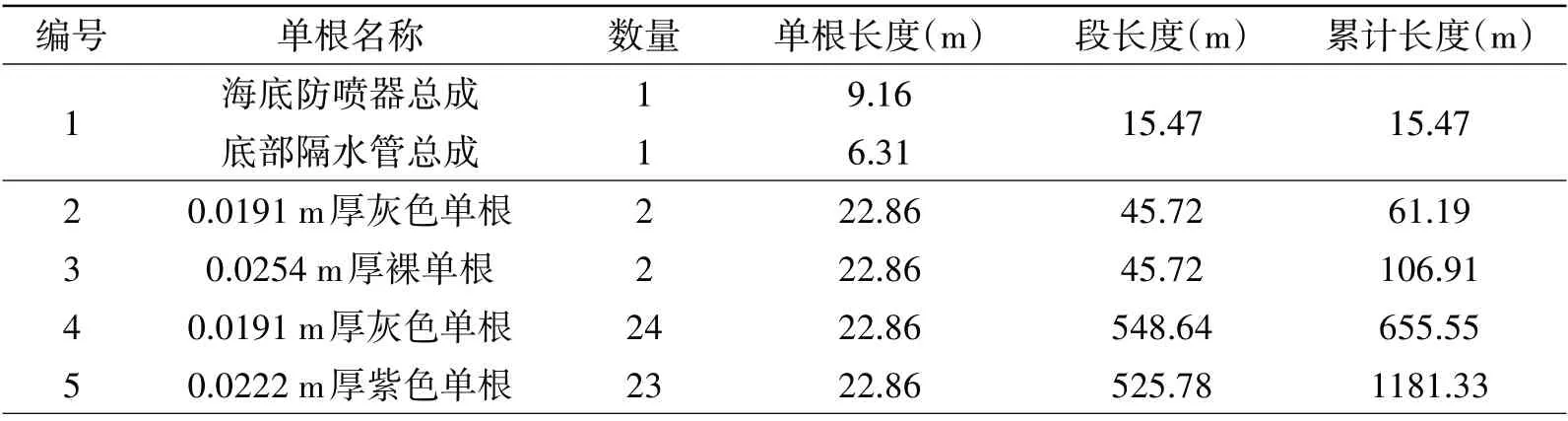
表3 中国南海某井隔水管实际配置Tab.3 Riser stack-up for one deep-water well in South China Sea

续表3

5.1 正常连接工况隔水管动力特性与强度分析

5.1.1 正常连接隔水管安全分析

图10展示了一年至二百年一遇的海流作用下正常连接隔水管变形及应力分布。可以看出，隔水管变形在中部1156.7 m处达到最大值，Von Mises应力在2170 m水面位置达到最大值。由于隔水管所受载荷与流速大小成正比，隔水管的位移、应力随着流速增大而增大[11,26]。另外，由于水面是海流载荷边界，隔水管应力在此出现最大值；而上下连接部位采用的是挠性接头连接，使得隔水管应力较小[34-35]。应力曲线在顶端及底端附近出现波动主要是由于浮力块在该区域配置不同引起载荷及隔水管弯曲刚度的变化导致。研究发现，正常连接隔水管的应力通常会先于顶端与底端转角达到极限值，因此主要从应力角度对正常连接隔水管进行安全分析。隔水管在一、五、十年一遇的载荷作用下，最大应力都低于警戒应力，在十年至一百年一遇的载荷作用下最大应力超过警戒应力，在二百年一遇的载荷作用下最大应力超过屈服应力。

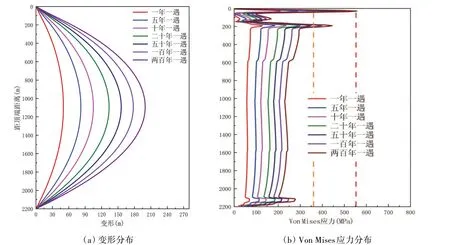
图10 不同海流流速作用下隔水管动力特性Fig.10 Influence of current velocity on the mechanical behavior of riser

5.1.2 平台漂移距离分析

平台漂移距离通常用隔水管长度的百分比来表示，分析时视漂移方向与海流方向相同。当平台分别漂移1%、2%、3%时，隔水管的位移和Von Mises应力分布随载荷变化分别如图11～13所示。从图中可以看出，隔水管变形和Von Mises应力随着漂移距离的增大而增大。当偏移量为1%时，隔水管能承受五年一遇的流速载荷；当偏移量为2%时，隔水管能承受一年一遇的流速载荷；当偏移量为3%时，隔水管连一年一遇的流速载荷都不能承受。因此，当海流速度变化时，必须严格控制平台漂移以保证隔水管的安全，在漂移比率达到3%时，应及时调整平台位置或者采取解除隔水管连接等应急措施[11]。

图11 平台漂移1%时不同海流流速作用下隔水管动力特性Fig.11 Influence of current velocity on the mechanical behavior of riser with platform drifting distance of 1%

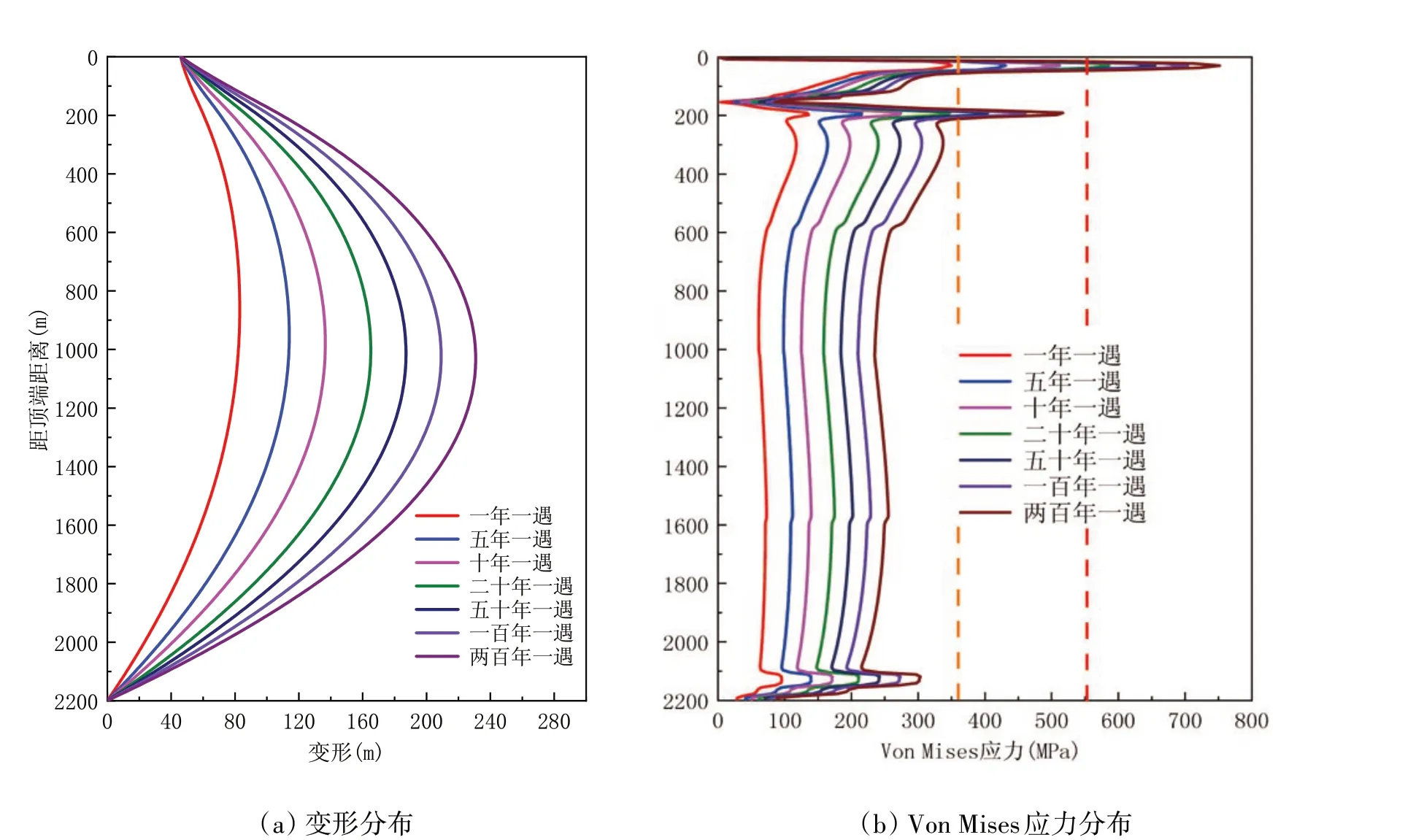
图12 平台漂移2%时不同海流流速作用下隔水管动力特性Fig.12 Influence of current velocity on the mechanical behavior of riser with platform drifting distance of 2%

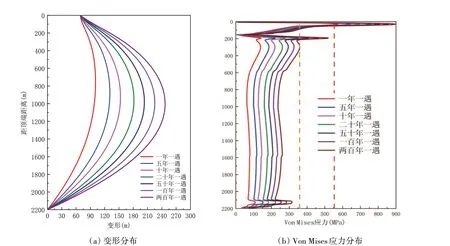
图13 平台漂移3%时不同海流流速作用下隔水管动力特性Fig.13 Influence of current velocity on the mechanical behavior of riser with platform drifting distance of 3%

5.1.3 平台漂移方向分析

上述漂移比率分析基于平台漂移方向沿海流流速方向，而实际平台可能向各个方向漂移。因此，本节以警戒应力及转角极限为条件，分析当平台向各方向漂移时隔水管所能承受的最大海流载荷。当漂移比例分别为1%、2%、3%时，各个漂移方向隔水管承受海流载荷能力如图14 所示。隔水管可承受的流体速度从0°到90°逐渐增大，从90°到180°又逐渐减小，在180°～360°方向的变化趋势相同。平台漂移1%时安全海流流速为1.40 m/s，即五年至十年一遇的海流载荷；漂移2%时安全海流流速为1.29 m/s，即一年至五年一遇的海流载荷；漂移距离为3%时安全海流流速为0.97 m/s，即一年一遇的海流都不能承受。

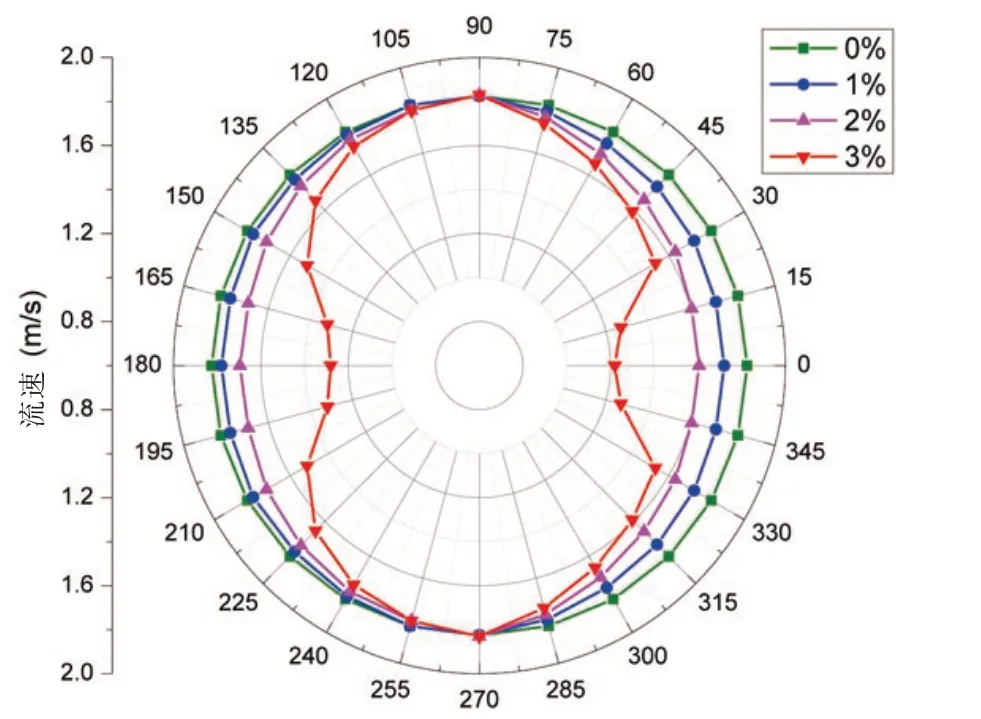
图14 不同漂移方向隔水管安全流速分布图Fig.14 Maximum current loads that the riser can withstand with platform drifting in all directions

5.2 悬挂撤离工况隔水管动力特性与安全分析

隔水管悬挂撤离时，假设平台以1 kn（0.5144 m/s）的固定速度沿着海流流速方向进行撤离。图15是海流速度为一年至二十年一遇时硬悬挂模式下隔水管的变形、弯矩和Von Mises应力分布图。可以看出，隔水管位移随着水深增加而增加，并且在悬挂底端达到最大值；隔水管弯矩和Von Mises应力在顶端处达到最大值。由于硬悬挂隔水管上端固定于平台上，连接处会产生应力集中现象[36-37]，该位置极容易发生危险。另外，从图15（c）可以看出Von Mises应力在底端附近有所增大。将应力计算式（7）中根号下各项拆分，第一项(σr-σ0)2只含径向应力与周向应力，如图16左图所示沿水深呈现指数式增长，并在底端达到最大值，因此各项相加后底端附近应力值出现增加现象。随着流速的增加，海洋环境载荷增大，隔水管的位移、弯矩、Von应力均相应地增大。当流体速度达到一年一遇时，隔水管最大应力小于警戒应力，当流体速度达到五年一遇载荷时，隔水管最大应力将超过屈服应力，可能发生断裂。

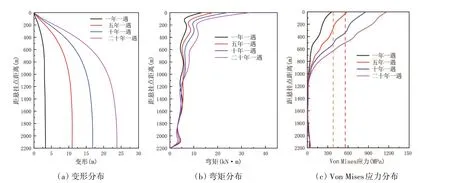
图15 不同海流流速作用下硬悬挂隔水管动力特性Fig.15 Influence of current velocity on the mechanical behavior of riser under hard hang-off condition

图16 硬悬挂隔水管Von Mises应力拆分Fig.16 Separated Von Mises stress of hard hang-off riser

图17 是海流速度分别为一年至二十年一遇时软悬挂模式下隔水管的变形、弯矩、Von Mises 应力及顶端转角分布图。可以看出隔水管位移随着水深增加而增加，并且在底端达到最大值。隔水管弯矩和应力在水面位置附近达到最大值，但在最顶端迅速减小趋于0，这与正常连接工况类似，是由水面载荷边界及顶端挠性接头转动共同作用的结果[38-39]。当流体速度达到为一年一遇时，隔水管最大应力小于警戒应力，当流体速度达到五年一遇时，隔水管最大应力超过警戒应力，但小于隔水管屈服应力。另外，由图17（d）可知，当流速达到五年一遇时，软悬挂隔水管顶端转角将超过转角限制，可能造成上部挠性接头破坏甚至断裂。

图17 不同海流流速作用下软悬挂隔水管动力特性Fig.17 Influence of current velocity on the mechanical behavior of riser under soft hang-off condition

6 结 论

本文建立了适合正常连接工况与悬挂撤离工况的隔水管动力分析模型，开展实验验证了模型的正确性。以中国南海深水井为实例，对正常连接与悬挂撤离工况下隔水管动力特性进行了分析，并对不同海况、工况下隔水管的漂移限制及应力安全进行了校核和讨论，得到如下主要结论及建议：

（1）正常连接工况下，隔水管最大应力出现在水面位置附近，容易发生破坏。因此在水面位置附近应当通过增加隔水管壁厚来增强隔水管强度，并取消布置浮力块以减小该段隔水管所受海洋环境载荷。

（2）平台未发生漂移情况下，隔水管能够承受十年一遇及以下的载荷；在十年一遇以上的载荷作用时隔水管存在发生破坏危险，需要加强监视，必要时采取应急措施。

（3）平台漂移后隔水管变形和应力都会增大，因此必须严格控制平台偏移量，在漂移比率达到3%时应及时调整平台位置或者采取解除隔水管连接等应急措施。另外，当平台漂移方向与流体流动方向直线夹角越大时有利于减小隔水管的安全威胁。

（4）隔水管悬挂撤离时，若采用软悬挂模式，水面位置附近出现极大应力；若采用硬悬挂模式，隔水管在与平台连接处出现极大应力。隔水管极大应力出现位置存在破坏断裂危险，需要加强监视，并适当增加强度。

（5）与硬悬挂模式相比，软悬挂模式下隔水管整体弯矩与应力都更小，但是由于顶端转角较大容易造成上部挠性接头破坏，软悬挂模式下隔水管所能承受海流作用能力并不能显著优于硬悬挂。因此，平台撤离时不能盲目采用软悬挂或硬悬挂模式，应当结合实际情况选择合适的悬挂模式。