水下爆炸数值模拟联合算法求解结构稳态响应

李亚伟， 杜志鹏， 李 俊， 李晓彬， 张 磊

(1.武汉理工大学 交通学院， 湖北 武汉 430063； 2.海军研究院， 北京 100161)

0 引 言

加筋板架是船体结构最基本的组成部分[1]，加筋板结构的设计与水面舰船的好坏有直接关系，关于加筋板架的研究[2]至关重要。JIANG等[3]考虑流固耦合和应变率效应，提出一种简化的理论分析方法，用于计算板架水下爆炸动塑性响应。吴有生等[4]研究在爆炸载荷作用下舰船板架的变形与破损，并在试验中得到了较好的验证。GUPTA等[5]对船体板架结构用ABAQUS/Explicit进行仿真，计算板架弹塑性变形与破坏。牟金磊等[6]用MSC.Dytran对不同药量、不同爆距下的板架毁伤模式进行仿真研究，并进行试验验证。王龙侃等[7]用ABAQUS/Explicit对加筋板架进行水下爆炸响应仿真计算，得到加筋板架的变形与破损，并对比仿真结果与试验结果。综合上述分析发现，以往基于ABAQUS的水下爆炸数值模拟方法都是基于瞬态显式求解器设置的，而显式求解器在求解加筋板架的稳态响应方面存在一定的缺陷，即加筋板架变形在最终塑性变形位置处无限振荡，从而可能导致仿真结果被低估或误判(取值误差)。鉴于此，提出采用“瞬态显式-稳态隐式”联合数值仿真方法求解加筋板架动力响应。该方法基于ABAQUS/Explicit-Standard算法，针对瞬态显式和稳态隐式静力平衡迭代建立联合仿真分析方法。该方法在求解结构稳态响应时能够有效避免瞬态显式分析结果中存在的缺陷问题。

1 稳态响应

在水下爆炸冲击作用下，加筋板架遭受冲击载荷后产生弹塑性变形，并在弹塑性变形最大时发生回弹，然后在最终塑性变形位置振荡并无限趋近于最终塑性变形。从变形回弹到无限趋近于最终塑性变形的过程称为稳态响应，具体如图1所示。

图1 水下爆炸加筋板架变形时历曲线

1.1 瞬态显式求解稳态响应

采用瞬态显式中心差分法对稳态响应求解，将板架结构的稳态响应处理成自由振动问题，引入适当的阻尼项来消除引起的动态振荡，使板架在一段时间后达到稳定状态[8]。施加黏性阻尼系统的动态平衡方程为

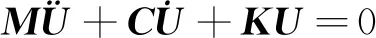
(1)

式中：M、C、K分别为结构质量、阻尼、刚度矩阵；U为节点位移向量。对于一个简单地施加临界阻尼的振荡系统，系统位移为

u=αe-ω t+βte-ω t

(2)

式中：ω为自然角频率；α、β为与边界条件、几何、材料性质有关的系数；t为时刻。

1.2 隐式算法求解稳态响应

采用隐式求解算法计算板架的稳态响应过程。此时板架所受载荷已远小于爆炸冲击载荷，几乎可忽略不计。因此，隐式算法将板架稳态响应看作是一个拟静态的响应过程，采用增量形式的虚功方程求解整个板架的非线性方程组，并采用静力平衡迭代的方法求解板架的稳态响应，即隐式算法求解稳态响应的过程。

隐式算法计算得到的稳态响应结果可靠性强、计算效率高，而采用瞬态显式算法求解稳态响应必须引入合适的阻尼系数，且引入的系数又缺乏明确的物理意义。因此，本文提出一种联合“瞬态显式-稳态隐式”算法的有限元仿真分析方法，该方法基于ABAQUS中的瞬态显式动力求解与隐式静力分析。

2 加筋板架瞬态-稳态响应分析

2.1 加筋板架模型

根据文献[1]和文献[7]中的加筋板架试验模型，分别对加筋板架进行仿真研究，并将仿真结果与试验结果进行对比验证。加筋板架模型如图2所示。所有模型材料均采用Q235钢。采用有限元软件ANSA对加筋板架及流场水域进行前处理。其中，模型2加筋板架及流场水域的有限元模型如图3所示。

在仿真分析时，炸药选用TNT装药，炸药均放置在加筋板架正下方，加筋板架边界条件为四周刚性固定，试验工况如表1所示。采用Geers-Hunter的水下爆炸双重渐近模拟计算水下爆炸载荷。由于只关注冲击波载荷对结构的影响，因此只需将爆炸载荷加载时间设置为小于气泡脉动周期即可。

表1 2种模型水下爆炸计算工况

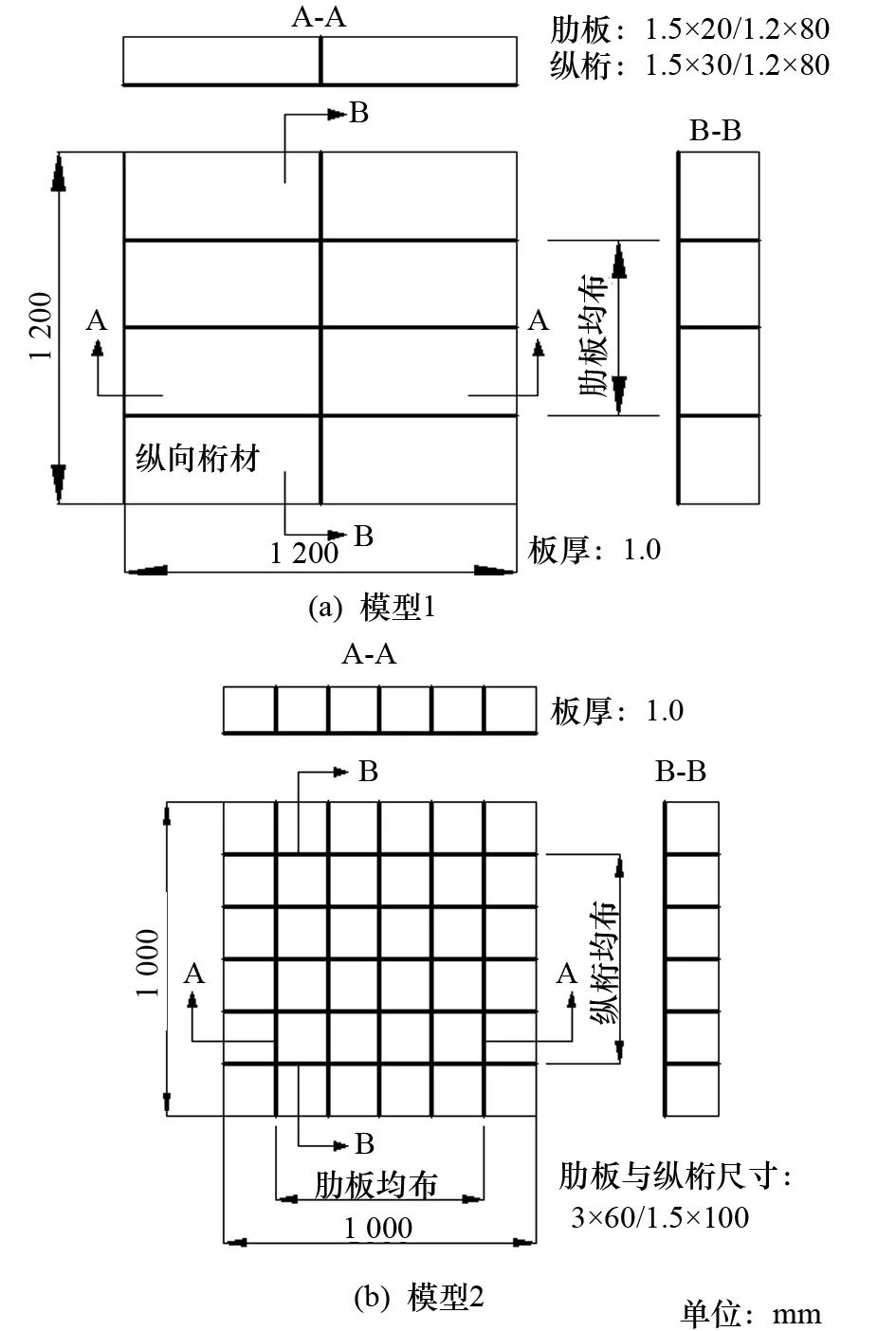
图2 加筋板架模型

图3 模型2加筋板架及流场水域的有限元模型

2.2 瞬态显式仿真结果与试验结果分析

采用瞬态显式法对船体板架结构有限元模型进行计算，计算结果如图4所示，为模型1与模型2在特定时刻的变形云图。由图4可知：在水下爆炸载荷作用下，加筋板架发生大幅度的塑性变形，且不存在缺口，即加筋板架的破坏模式为塑性大变形。

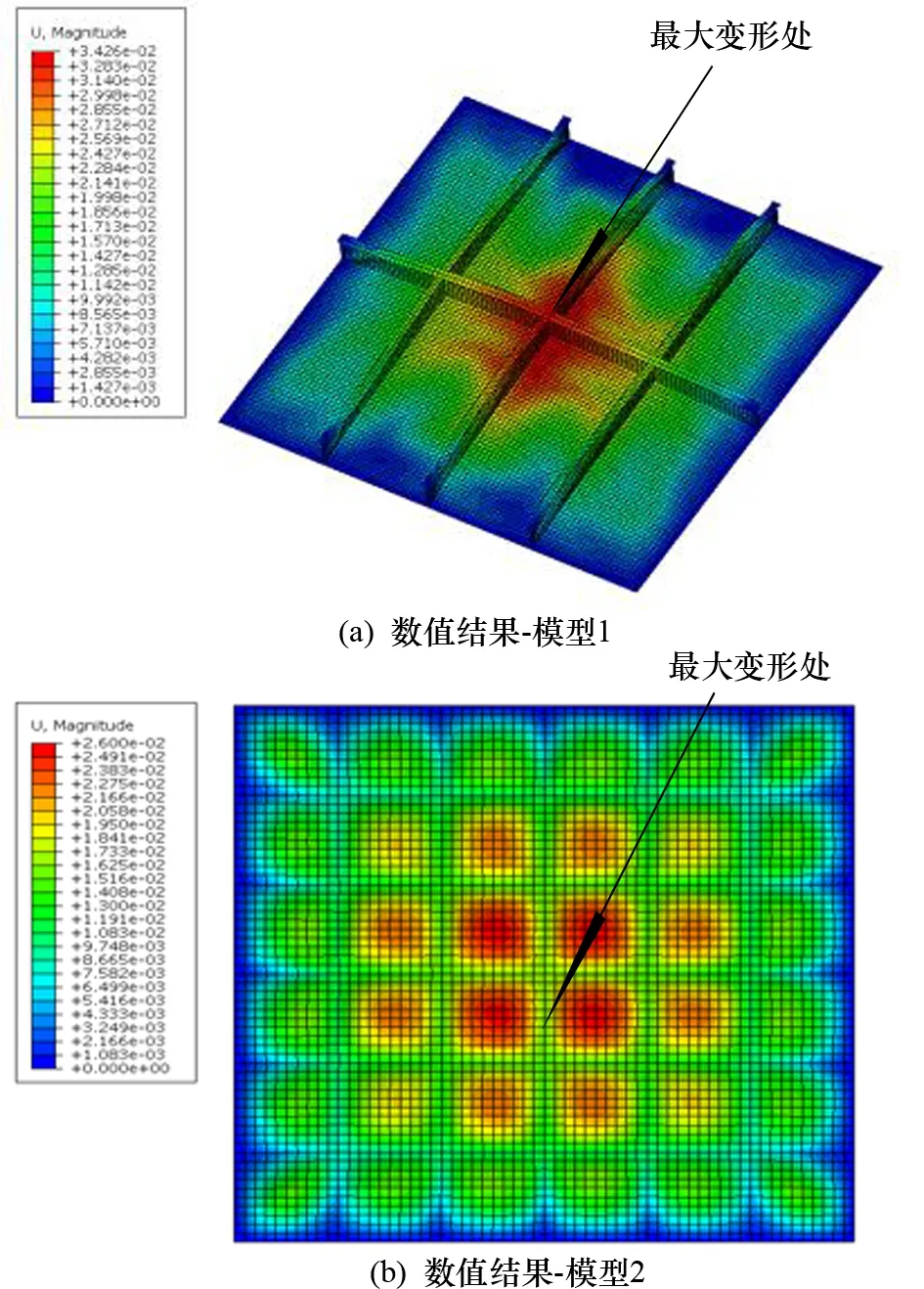
图4 加筋板架0.15 s时刻爆炸冲击变形云图

图5所示为模型2在试验中加筋板架的整体塑性变形图，其最终变形挠度为15.79 mm。图4(b)为模型2在特定时刻的数值模拟塑性变形云图，其最终变形挠度为17.50 mm。

图5 模型2加筋板架0.15 s时刻整体塑性变形图

根据对数值仿真结果的分析，可以得出这2种加筋板架模型的变形值。表2给出了2种模型其加筋板架的仿真值与试验实测值。从表2可以发现，这两种模型的仿真误差都在10%以上。

表2 2种模型的加筋板架仿真值与试验值对比

2.3 瞬态显示-稳态隐式联合仿真结果与试验结果分析

(1) ABAQUS隐式算法对加筋板架稳态响应求解具体分析步骤如下。

① 首先，需导入冲击变形后的加筋板架。在环境栏Module后面选择part，进入part分析模块，并导入瞬态计算完成的.odb文件，选择分析步中的最后一个增量步，即可导入变形的加筋板架。

② 装配加筋板架并创建分析步。环境栏切换至Assembly模块，将加筋板架加载到装配体，然后切换到Step模块，打开非线性，因为内应力突然释放，为稳定收敛，设置自动稳定因子，分析步初始增量尺寸值可以设为0.1。

③ 施加边界条件并引入瞬态变形结果。切换至Load模块，对沿x方向的边界施加关于与x轴(坐标轴1)垂直的平面反对称边界条件，对沿y方向平行的边界施加关于与y轴(坐标轴2)垂直的平面反对称边界条件。在菜单栏Predefined Field中创建一个初始状态，输入之前瞬态变形生成的job文件，则瞬态变形后的加筋板架(变形网格、硬化材料属性、应力应变等)会替换本模型中的加筋板架。

④ 创建并提交分析。在求解结束后，即可进入后处理，查看稳态变形结果[9-12]。

(2) 采用瞬态显式-稳态隐式联合算法计算加筋板架稳态响应。

以模型2的仿真分析为例，采用联合算法计算模型2加筋板架的稳态响应问题。具体方法如上所述：首先将瞬态显式算法计算完成的结果文件导入ABAQUS中；然后创建并设置分析步，分析步采用稳态隐式静力分析；最后提交作业分析，并查看最终仿真结果。

图6(a)所示为模型2在0.02 s时刻的塑性变形云图，其最终变形挠度为17.50 mm；图6(b)为加筋板架在瞬态显式计算完成后，采用稳态隐式算法计算完成后的稳态响应变形云图。稳态前的位移参考值被重置为0，故稳态分析的位移即为稳态变形值。由图6(b)可知，稳态最大变形量为0.68 mm。

图6 水下爆炸作用下加筋板架瞬态-稳态响应变形云图(模型2)

为更清晰地观察加筋板架的挠度变化，图7(a)与图7(b)分别给出加筋板架采用“瞬态显式-稳态隐式”联合算法和单独采用瞬态显式方法的加筋板架中心点处垂向位移时历曲线对比图。

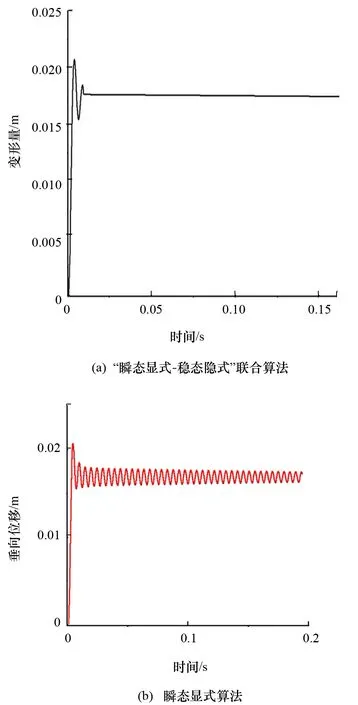
图7 采用两种不同算法的加筋板架垂向位移时历曲线(模型2)

由图7(a)和图7(b)可知，单独采用瞬态显式算法得到的仿真结果中可能存在取值误差。“瞬态显式-稳态隐式”联合算法仿真结果不存在取值误差缺陷。表3给出了联合算法的仿真结果与试验结果的对比分析值。

表3 “瞬态显式-稳态隐式”联合算法加筋板架仿真值与试验值对比

由表3可知：采用联合“瞬态显式-稳态隐式”算法得到的仿真结果与试验值的误差约6.5%，与单独采用瞬态显式算法的仿真结果相比，误差降低约39.8%，说明在采用联合“瞬态显式-稳态隐式”算法仿真计算时，在排除取值误差的缺陷后，得到的加筋板架稳态变形的仿真结果更接近试验值。

3 结 论

采用ABAQUS“瞬态显式-稳态隐式”联合算法，计算船体加筋板架在水下爆炸作用下的稳态响应，求解加筋板架在水下爆炸冲击载荷下的稳态变形特性，并将数值仿真结果与试验结果进行对比分析，结论如下：

(1) 采用“瞬态显式-稳态隐式”联合算法得到的结果与试验结果相差在10%以内，说明该算法的仿真方法可用于水下爆炸作用下结构的动力响应数值模拟分析。

(2) 采用联合“瞬态显式-稳态隐式”算法仿真得到的稳态变形值比采用瞬态显示算法更接近试验值。由于联合算法在稳态响应分析时释放了瞬态响应阶段的残余应力和应变，因此此时的稳态变形更接近试验值。这说明，在瞬态响应分析的基础上，稳态隐式静力平衡分析能够提高加筋板架数值仿真的变形精度。