布置方案对近海小型无人监测船波浪运动的影响

路骄阳， 岳前进， 张大勇， 苏学荣

(1.大连理工大学 海洋科学与技术学院， 辽宁 盘锦 124221； 2.北部战区海军91040部队， 山东 青岛266000)

0 引 言

海洋覆盖地球表面的70%以上，包含地球上大约90%的生命形式。它们是食物、就业和经济收入的主要来源之一，是仍然未知的生物、矿产资源以及可持续能源的潜在来源[1]。在人类开发和可持续利用海洋资源的过程中，海洋监测技术是一种必不可少的手段，发展海洋监测技术具有重要意义。例如：海洋能源的开发需要及时、准确地观测预报服务[2-3]；建设海洋牧场、修复海洋渔业资源需要加强对海洋环境的监测[4]；保护海洋环境、治理海洋污染需要发展污染和生态环境监测技术，提高监测能力[5]。

传统的海洋监测手段包括船舶走航、卫星遥感、沿岸监测站、海洋浮标等[6]。每种方法都有一定的局限性：船舶走航测得的数据样本少，周期长，成本高；卫星遥感准确度不高，可测参数种类少；沿岸监测站只能获取近海资料；海洋浮标的设计、布置和维护均比较困难[7-8]。近年来，随着人工智能技术、控制技术、导航定位技术的飞速发展，无人监测平台成为海洋监测技术的一大研究热点[9]。

小型无人监测船具有成本低、作业高效、工作范围广、数据可靠等一系列优点。然而，由于近海海域水深较浅、离陆地较近，波浪、海流等容易受地形因素的影响，形成较为复杂的海洋环境[10]。另外，由于自身尺度原因，小型无人监测船极易在波浪中发生较大幅度的运动，这些运动轻则会导致传感器测出的数据不够准确，无法正常工作，重则可能导致仪器损坏，甚至使船发生倾覆。因此，如何减小小型无人监测船在波浪中的运动，是设计者必须考虑的问题。然而，目前国内外针对小型无人监测船的研究大多集中于避障[11]、运动控制[12]、路径规划[13]等技术，针对船体波浪运动性能的相关研究较少，在船体设计过程中，船厂大多借鉴游艇、玻璃钢游乐船的相关设计经验[14]，产品运动性能较差，可靠性不高。

以一艘近海小型双体无人监测船为例，采用二维切片法进行数值计算，分析吃水深度、横摇惯性矩、纵摇惯性矩、重心高度对近海小型无人监测船波浪运动的影响，得出一系列结论，可为小型无人监测船布置方案设计提供参考。

1 船型参数及数值计算方法

1.1 船型主尺度

与传统单体船相比，双体船宽度更大，具有甲板开阔、横摇稳心半径大、兴波阻力小、耐波性好等一系列优点[15]，因此市场上的小型海洋无人监测船多采用双体船的结构型式。考虑到这一因素，以大连理工大学海洋科学与技术学院自行设计的小型双体无人监测船为例进行相关计算分析，其主尺度如表1所示。

表1 自行设计的小型双体无人监测船主尺度 m

无人监测船需搭载的主要设备包括：环境监测相关传感器、电池、推进器、控制板等。船体模型如图1所示。

图1 小型双体无人监测船模型

1.2 数值计算方法

船舶摇荡运动是一种六自由度运动，分别称为横摇、纵摇、艏摇、横荡、纵荡和垂荡，其中横摇、纵摇、垂荡对无人监测船工作影响最大。本文的计算过程主要关注这3个自由度的运动响应。

目前在船舶水动力研究领域，主要采用流体力学中的势流理论对船舶在波浪中的运动响应进行预测，具体包括基于平面势流理论的切片法、基于三维势流理论的面元法等。二维切片理论的优势在于：在浮体满足细长体假设的前提下，可以运用频谱分析方法预报不同波长、浪向和航速的浮体在给定波谱下的运动。该理论计算过程耗时较少，精度结果比较理想。考虑所用模型满足细长体假设，故使用二维切片法对无人监测船进行频域分析，水动力模型如图2所示。具体计算理论在文献[16-17]中已有详细的描述，不再赘述。

图2 无人监测船二维切片法模型

2 计算结果及分析

该小型无人监测船主要应用于渤海，取波浪角为45°，计算并分析不同布置方案，包括吃水深度、横摇惯性矩、纵摇惯性矩、重心高度等对其运动性能响应的影响。

2.1 吃水深度对无人监测船运动性能的影响

无人监测船吃水深度直接关系到可搭载设备的种类与数量。在安全范围内，尽量增加无人监测船的吃水深度，搭载更多环境监测传感器，可提高经济效益。本节详细分析吃水深度对无人监测船运动性能的影响，以期为无人监测船设计过程中吃水深度的选取提供参考依据。

针对上述无人监测船模型，在计算过程中，保持无人监测船重心高度、横纵摇惯性矩不变，设置吃水深度分别为0.10 m、0.15 m、0.20 m、0.25 m和0.30 m，对其横摇、纵摇、垂荡等3个自由度的运动响应进行分析。

幅值响应因子也称为传递函数，描述了浮体运动响应如何随波浪频率变化，是浮体运动性能的重要表征参数。在计算与分析过程中，重点关注这一参数随吃水深度变化的规律，具体结果如图3～图5所示。

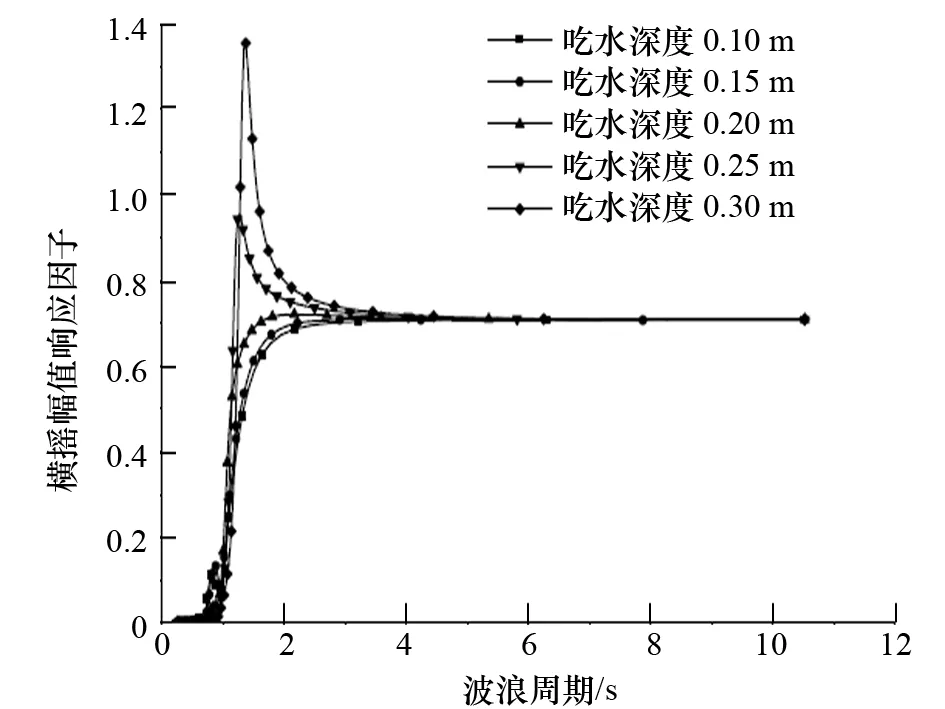
图3 吃水深度对横摇运动的影响

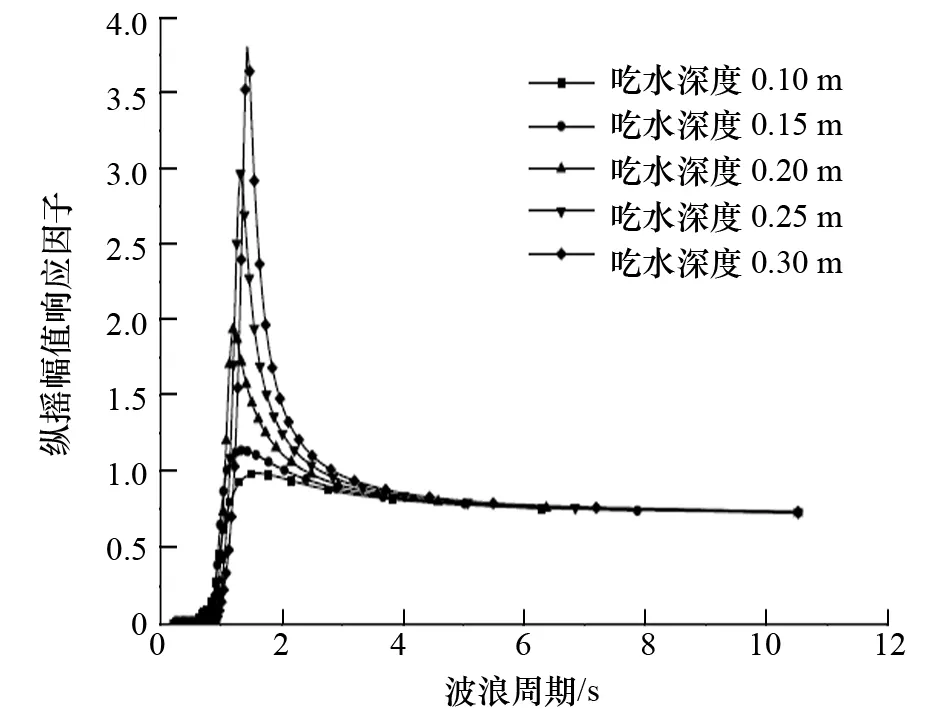
图4 吃水深度对纵摇运动的影响

图5 吃水深度对垂荡运动的影响

分析图3～图5中各自由度的运动响应因子随吃水深度的变化情况可以发现：

(1) 吃水深度对3个自由度的运动性能均有一定影响。随着吃水深度增加，横摇、纵摇、垂荡运动逐渐增大，响应幅值先向高频再向低频移动。

(2) 当吃水深度超过0.2 m后，各自由度运动响应随吃水深度增加而急剧增大。

(3) 各自由度最大幅值响应对应的周期大致在1～2 s，这一结果已远离渤海海浪能量集中区4.5～4.8 s[17]。当波浪周期大于3 s后，运动响应已处于较低水平。

(4) 吃水深度对纵摇、垂荡运动的影响略微大于对横摇运动的影响。

根据上述结果，在设计无人监测船吃水深度时，由于吃水深度对3个自由度的运动响应均具有明显影响，应对3个自由度的运动响应进行综合考量。在通常情况下，在一定范围内考虑对吃水深度进行适当增加。无人监测船运动响应虽会随吃水深度增加而增加，但增幅并不明显，仍处于安全范围。在超过这一范围后，增加无人监测船的吃水深度会使3个自由度运动响应急剧增加，在遭遇低周期海浪时可能会发生危险。

2.2 惯性矩对无人监测船运动性能的影响

惯性矩与无人监测船搭载仪器在相应方向上的布置有关。研究惯性矩对无人监测船运动响应的影响可以为无人监测船搭载仪器在相应方向上的布置方案提供依据。引入参数k表征惯性矩相对于长度和宽度的百分比，其表达式为

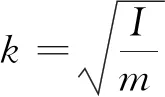
(1)

式中：I为对应方向的惯性矩；m为物体质量。

在计算横摇惯性矩影响的过程中保持无人监测船重心高度、纵摇惯性矩、吃水深度不变，设置k分别为10%、20%、30%、40%、50%、60%，计算结果如图6～图8所示。

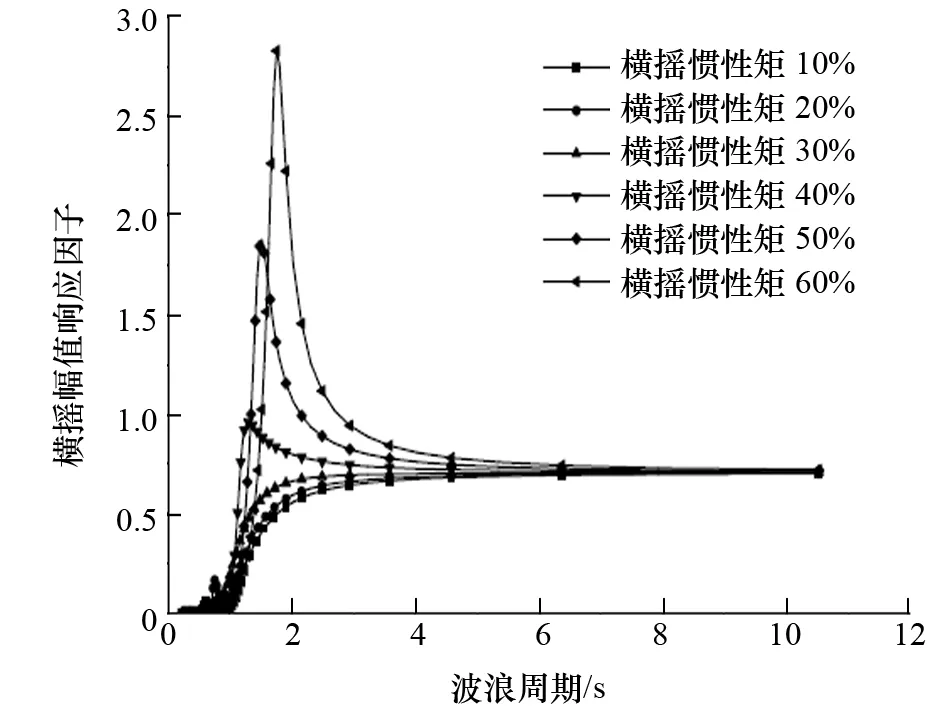
图6 横摇惯性矩对横摇运动的影响

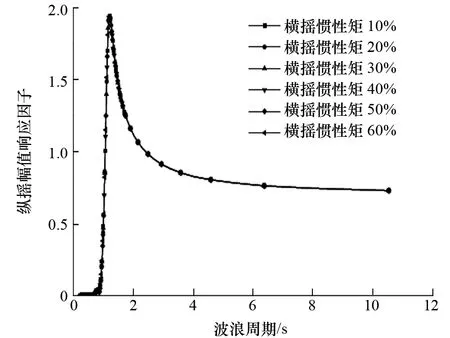
图7 横摇惯性矩对纵摇运动的影响

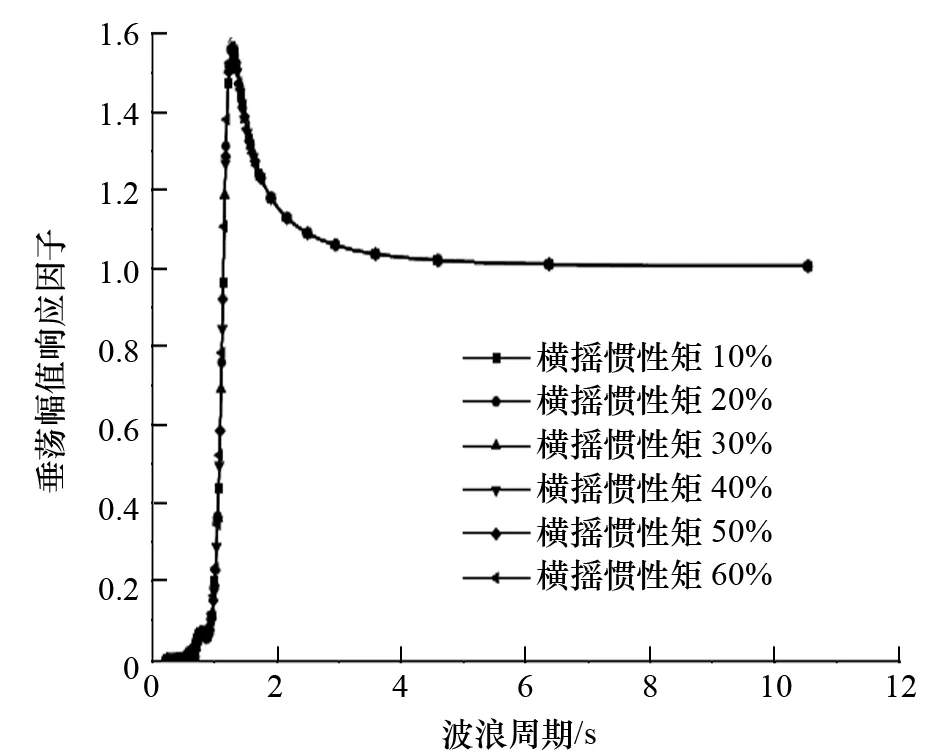
图8 横摇惯性矩对垂荡运动的影响

分析图6～图8中各自由度的运动响应因子随横摇惯性矩的变化情况可以发现：

(1) 横摇惯性矩对横摇运动具有明显影响。横摇运动随着横摇惯性矩的增加而逐渐增大，响应幅值先向高频再向低频移动。

(2) 当横摇惯性矩超过30%后，横摇运动响应随横摇惯性矩增加而急剧增大。

(3) 横摇惯性矩对无人监测船纵摇、垂荡运动性能几乎没有影响。

(4) 各自由度最大幅值响应集中在周期1～2 s，已远离渤海海浪能量集中区4.5～4.8 s。

在计算纵摇惯性矩影响的过程中保持无人监测船重心高度、横摇惯性矩、吃水深度不变，设置k分别为10%、20%、30%、40%、50%、60%，计算结果如图9～图11所示。

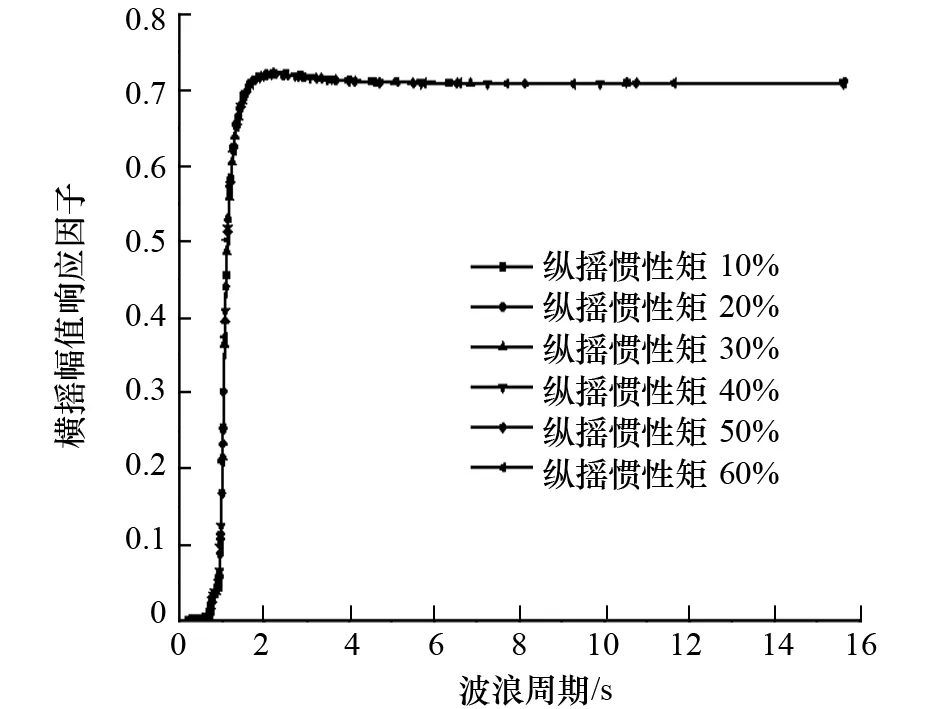
图9 纵摇惯性矩对横摇运动的影响

图10 纵摇惯性矩对纵摇运动的影响

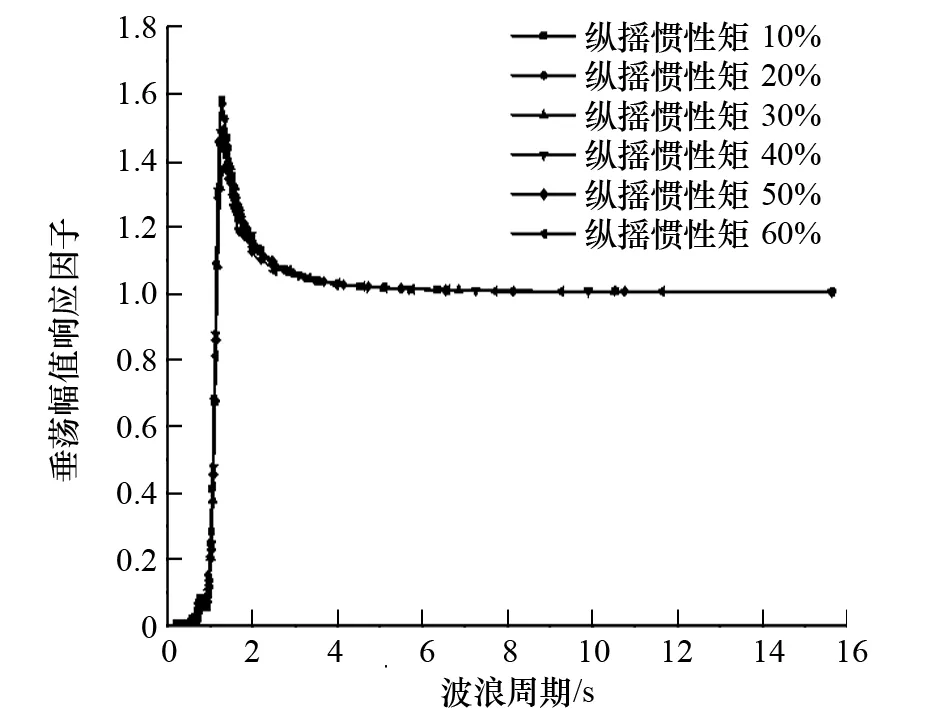
图11 纵摇惯性矩对垂荡运动的影响

分析图9～图11中各自由度的运动响应因子随纵摇惯性矩的变化情况可以发现：

(1) 纵摇惯性矩主要影响纵摇、垂荡的运动性能。随着纵摇惯性矩增加，纵摇运动显著增大，响应幅值先向高频再向低频移动。与此同时，随着纵摇惯性矩增加，垂荡运动先减小再增加，响应幅值先向低频再向高频移动。

(2) 纵摇惯性矩对纵摇运动的影响明显大于对垂荡运动的影响。

(3) 当纵摇惯性矩超过20%后，纵摇运动响应随纵摇惯性矩的增加开始迅速增大。当达到60%以后，响应幅值对应的波浪周期与渤海波浪能量集中区较为接近，极易发生大幅度运动。

(4) 纵摇惯性矩对无人监测船横摇运动性能没有明显影响。

根据上述结果，在对设备进行横向布置时，由于横摇惯性矩只对横摇运动具有明显影响，因此只需重点关注横摇的运动响应。在通常情况下，可以考虑在一定范围内适当增加横摇惯性矩。在这一范围内，无人监测船运动响应随横摇惯性矩增加缓慢，且幅值所对应周期逐渐减小，远离波浪能量集中区域，有利于改善横摇性能。在超过这一范围后，增加无人监测船的吃水深度会使运动响应急剧增加，幅值所对应的周期向低频移动，在渤海容易发生较大幅度的横摇。在对设备进行纵向布置时，由于纵摇惯性矩主要影响纵摇运动，且影响幅度远大于垂荡运动，因此主要考虑纵摇的运动响应情况，通常应尽量将其控制在较低范围内，避免纵摇幅值响应因子在遭遇低周期海浪时过大。

2.3 重心高度对无人监测船运动性能的影响

重心高度与无人监测船搭载仪器在垂向方向上的布置有关。分析重心高度对无人监测船运动响应的影响可在一定程度上为无人监测船搭载仪器在垂向方向上的布置方案提供依据。但需要注意的是，重心高度还是浮体稳性的重要影响参数，重心与浮心之间的高度关系会直接影响浮体的初稳性、大倾角稳性等，因此在设计过程中，重心高度的选取还应从稳性方面加以考量，使其达到稳性的要求。

在计算重心高度影响的过程中，保持无人监测船吃水深度、横纵摇惯性矩不变。考虑到船体自身尺寸，设置重心高度分别为0.10 m、0.15 m、0.20 m、0.25 m和0.30 m。计算结果如图12～图14所示。

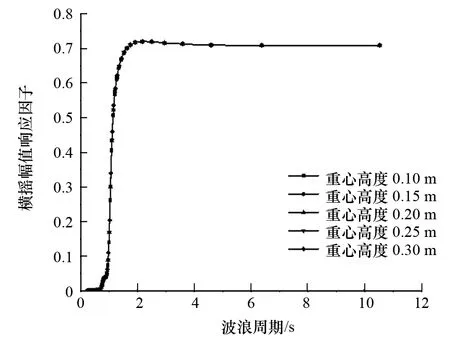
图12 重心高度对横摇运动的影响

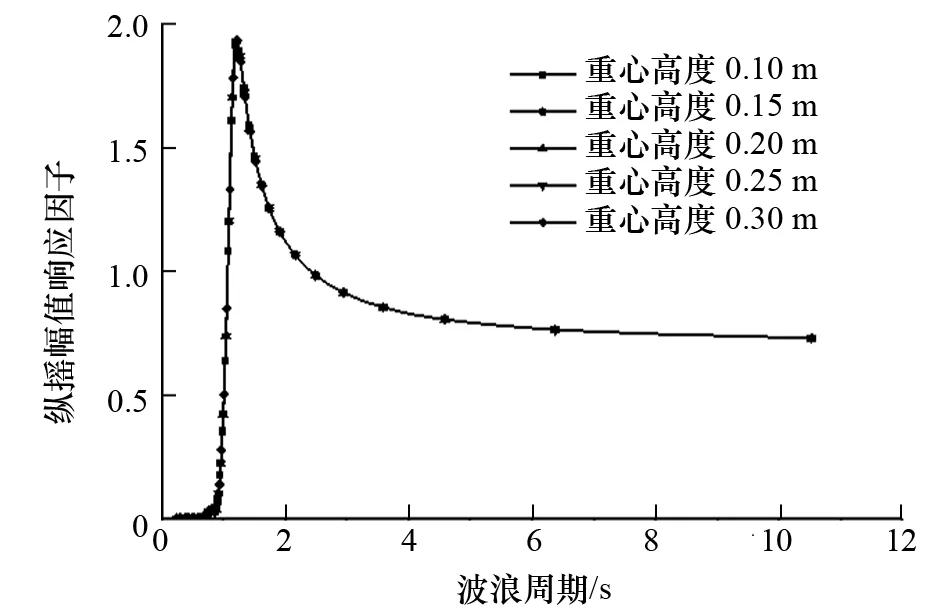
图13 重心高度对纵摇运动的影响

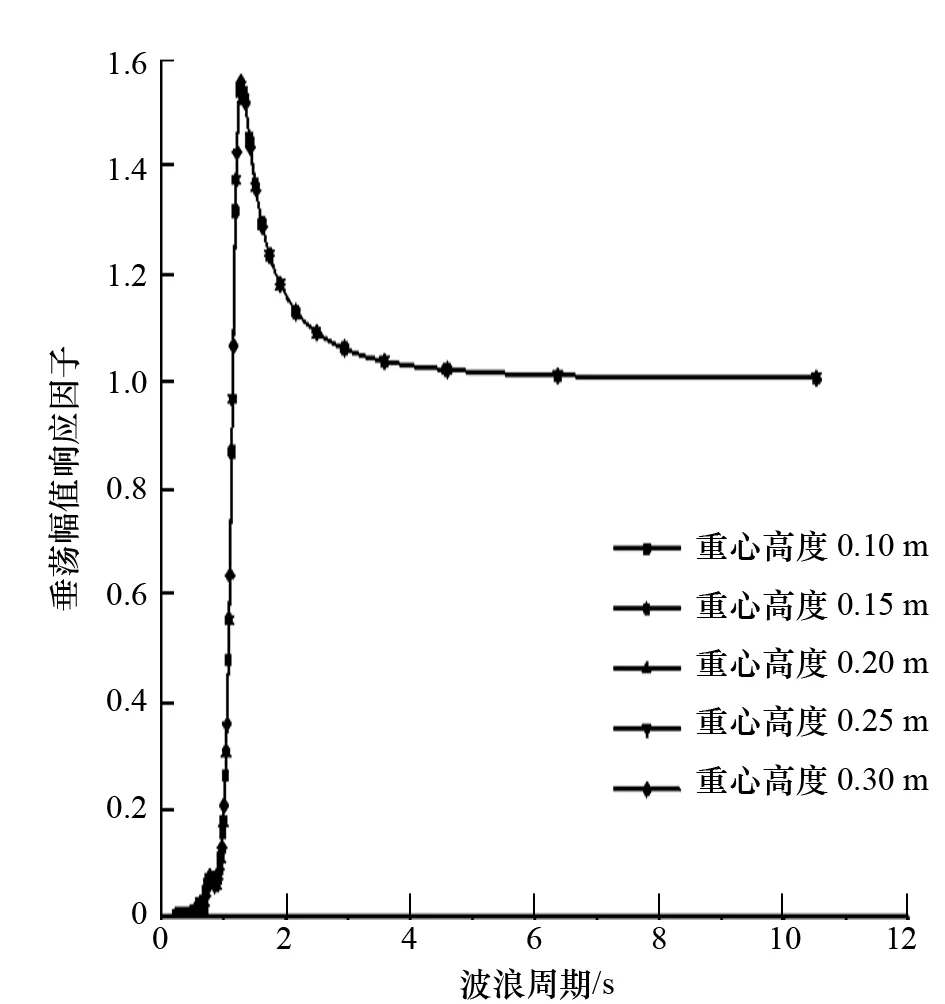
图14 重心高度对垂荡运动的影响

分析图12～图14中各自由度的运动响应因子随重心高度的变化情况可以发现：

(1) 重心高度对3个自由度运动性能的影响均不明显。

(2) 纵摇、垂荡的运动响应要明显大于横摇的运动响应。

上述结果表明，重心高度对无人监测船的运动响应影响不大。在设计无人监测船重心高度时，应主要从稳性的角度进行考虑，使无人监测船满足初稳性和大倾角稳性的相关要求。在通常情况下，应尽量降低重心高度，增大无人监测船的初稳心半径。但应注意的是，重心高度不宜布置得过低，否则无人监测船摇晃运动回复速度会过快，精密仪器难以正常工作。

3 结论与展望

运用二维切片理论，计算近海小型无人监测船在不同吃水深度、横摇惯性矩、纵摇惯性矩、重心高度等不同布置方案下在波浪中的运动响应情况，得出运动响应随布置方案变化的规律，并以此为依据提出一系列小型无人监测船仪器设备布置原则。

由于试验条件有限，仅运用数值计算的方法对布置方案与运动响应间的关系进行了初步的计算与分析，计算结果的准确性有待进一步通过试验进行对比。