带悬臂板薄壁箱梁极惯性矩的合理计算方法
张元海,刘泽翔,王晨光
(兰州交通大学 土木工程学院,甘肃 兰州 730070)
薄壁箱梁广泛应用于现代桥梁工程中,其扭转性能分析一直受到国内外学者的关注,文献[1-9]已发表了相关成果。在薄壁箱梁的约束扭转分析中,为了考虑二次剪切变形对纵向翘曲位移的影响,通常在自由扭转翘曲位移模式基础上,引入广义翘曲位移β′代替扭率φ′,即对自由扭转翘曲位移进行修正,将其作为约束扭转翘曲位移。建立约束扭转微分方程时,需要首先建立β′与φ′的关系式,其中会出现一个翘曲系数μ,即箱梁横截面极惯性矩和抗扭惯性矩之差与极惯性矩的比值[10-15]。翘曲系数μ是反映箱梁扭转时横截面翘曲程度的重要参数,它对约束扭转内力和应力都有直接影响。显然,合理计算极惯性矩是正确计算翘曲系数的基础。在分析薄壁箱梁的约束扭转时,文献[10-12]只在闭口范围内计算极惯性矩而未考虑悬臂板部分,文献[9,14-15]则在全截面上计算极惯性矩。由于极惯性矩与扭转中心(扭心)至壁厚中心线距离的平方成正比,按上述两种方法计算的结果将会相差较大,导致翘曲系数也相差较大。目前,对不同极惯性矩计算方法导致的约束扭转内力和应力变化的研究,尚未见文献报道。此外,为了简化计算薄壁箱梁的约束扭转几何特性,文献[16-19]推导了计算扭心位置、广义主扇性坐标及主扇性惯性矩等几何特性的实用公式,但没有涉及极惯性矩的计算。综上所述,有必要开展极惯性矩的合理计算及其对约束扭转内力和应力影响的研究。
本文在阐明薄壁箱梁翘曲系数的引入及极惯性矩合理计算方法的基础上,应用约束扭转微分方程的初参数解,结合简支箱梁数值算例,具体分析极惯性矩和翘曲系数的不同计算结果对约束扭转效应的影响规律,对合理计算极惯性矩提出建议。
1 极惯性矩和翘曲系数的引入
根据乌曼斯基第二理论及刚周边假设,薄壁箱梁发生约束扭转时,横截面壁厚中心线上任一点处的纵向翘曲位移u(z,s)和切向位移v(z,s)可分别表达为
(1)
v(z,s)=φ(z)ρ(s)
(2)
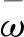
在箱梁横截面的闭口部分,箱壁厚度中心线上任一点处的剪应力τc为
(3)
式中:G为剪切模量;uc和vc分别为闭口部分壁厚中心线处的翘曲位移和切向位移,只需将式(1)和式(2)中的ρ改为ρc后即可得到uc和vc的表达式,ρc为扭心至闭口部分壁厚中心线的垂直距离。
将uc和vc的表达式代入式(3),可得
(4)
则横截面闭口部分剪应力合成的扭矩Mzc为
Mzc=∮τcρctds=GIρc(φ′-β′)+GIdβ′
(5)

在箱梁横截面上,悬臂板属于开口部分。悬臂板厚度中心线上任一点处的翘曲位移uo和切向位移vo分别为
(6)
vo(z,s)=φ(z)ρo(s)
(7)
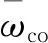
(8)
可以证明,薄壁箱梁发生约束扭转时,闭口箱室两侧悬臂板上的剪应力τo方向是相同的。故由τo合成的扭矩Mzo为
(9)

将Mzc与Mzo相加,可得横截面上的总扭矩Mz为
Mz=G(Iρc+Iρo)(φ′-β′)+GIdβ′=GIρ(φ′-μβ′)
(10)
式中:Iρ为箱梁横截面的极惯性矩,Iρ=Iρc+Iρo;μ为翘曲系数,μ=(Iρ-Id)/Iρ。
上述推演表明,计算薄壁箱梁横截面的极惯性矩时,应该在全截面上计算才合理。而文献[10-12]只在闭口范围内计算横截面的极惯性矩,这显然是不合理的。
应该指出,薄壁箱梁发生约束扭转时,无论在闭口箱壁还是悬臂板内,除前述剪应力外,还有沿壁厚呈线性分布的圣维南剪应力τs(在壁厚中心线处为0),但这部分圣维南剪应力对应的扭矩和抗扭惯性矩均较小,通常忽略不计。此外,不能直接按式(3)和式(8)计算约束扭转时的剪应力,而应按薄壁微元体平衡条件或根据自由扭矩和二次扭矩进行计算。
2 初参数解及其应用
根据薄壁箱梁的约束扭转理论,在式(10)基础上可建立关于扭转角φ的微分方程[10]
(11)

(12)

图1 跨中作用集中扭矩荷载的简支箱梁
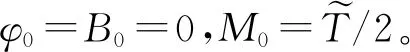
(13)
则箱梁任一截面的广义位移和内力为
(14)
(15)
(16)
(17)
(18)
(19)
式中:Md(z)为自由扭矩;Mω(z)为二次扭矩;M(z)为总扭矩;带有符号‖l/2的项表示只对z>l/2的截面才需计入该项。
3 数值算例分析

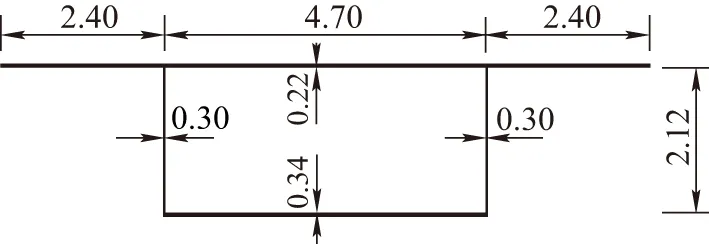
图2 简支箱梁横截面(单位:m)
分别使用翘曲系数的两个计算值μ1和μ2,应用薄壁箱梁约束扭转解析理论对距跨中2 m处横截面上的翘曲正应力进行计算,连同应用ANSYS有限元软件中SHELL63壳单元的计算结果一并示于图3中。箱梁共划分为13 200个壳单元、13 222个节点,跨中截面作用的集中扭矩荷载按静力等效的集中力施加在跨中截面闭口部分的各节点处。计算翘曲应力时,选取距跨中2 m处的横截面,主要是为了消除集中加载可能带来的应力集中影响。由图3可以看出,按解析法求得的翘曲正应力分布与壳单元结果相近,按全截面计算极惯性矩(相应翘曲系数μ1=0.300)求得的翘曲正应力与ANSYS壳单元结果吻合更好。
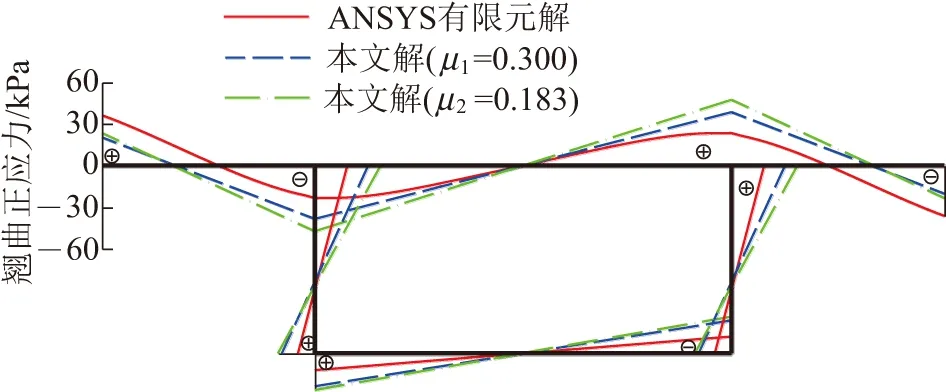
图3 距跨中2 m处横截面翘曲正应力对比
图4和图5分别为按约束扭转解析理论计算的对应于两个翘曲系数μ1和μ2的箱梁扭转角和广义翘曲位移分布。由图4可以看出,按两个翘曲系数计算的扭转角分布曲线几乎重合,即计算极惯性矩时是否考虑悬臂板,对扭转角计算结果几乎没有影响。由图5可以看出,计算极惯性矩时是否考虑悬臂板,对广义翘曲位移的影响也较小,影响主要体现在靠近跨中位置的截面处,当只按闭口截面计算极惯性矩时,求得的广义翘曲位移偏小。总之,按两种方法计算极惯性矩,对箱梁约束扭转位移计算结果的影响都不大。
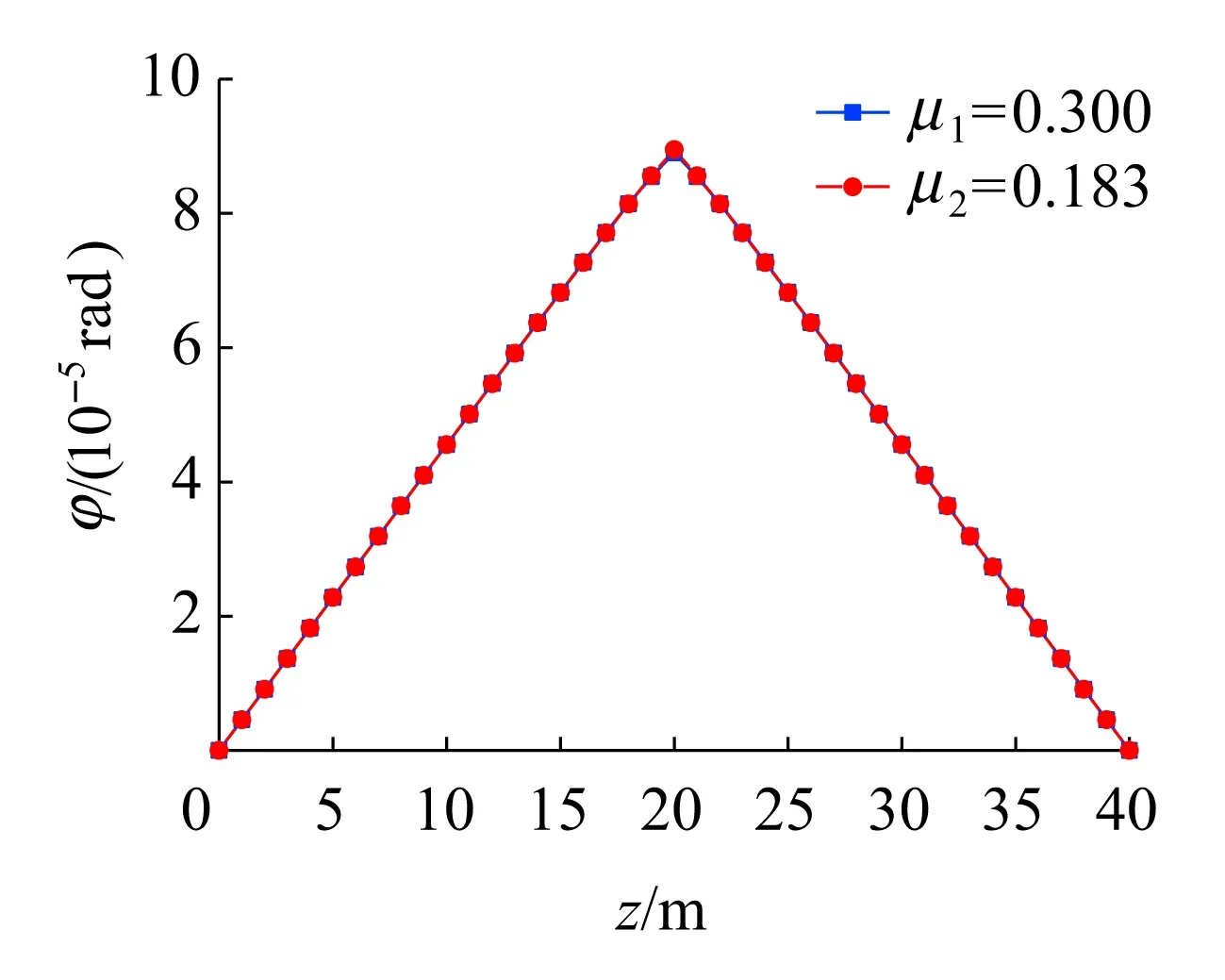
图4 简支箱梁扭转角分布对比

图5 简支箱梁广义翘曲位移分布对比
图6为按两个翘曲系数计算的双力矩分布。由图6可以看出,按两个翘曲系数计算的跨中截面双力矩有明显差别,对应于μ1和μ2的跨中双力矩分别为B1=241.4 kN·m2,B2=188.3 kN·m2,后者相对于前者约减小了22%,表明只在闭口部分计算极惯性矩时,将大幅低估跨中截面的实际双力矩。值得注意的是,在距离跨中约4 m处附近的截面内,只按闭口部分计算极惯性矩求得的双力矩比按全截面计算极惯性矩时求得的双力矩大,但差别不如跨中截面明显。
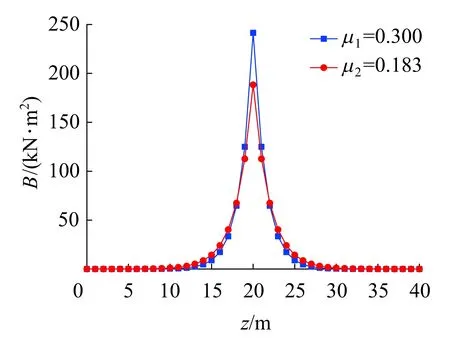
图6 简支箱梁双力矩分布对比
图7和图8分别为按两个翘曲系数计算的自由扭矩Md和二次扭矩Mω分布。由图7和图8可以看出,按两个翘曲系数计算的跨中左截面和右截面的自由扭矩和二次扭矩都有较大差别,只按闭口截面计算极惯性矩时,求得的跨中左截面处二次扭矩要比按全截面计算极惯性矩时求得的二次扭矩约减小39%,而自由扭矩约增大17%。与双力矩的分布类似,二次扭矩的分布也具有局部性,主要产生于跨中截面附近,二次扭矩在其余大部分梁段内均为0,即总扭矩只表现为自由扭矩。
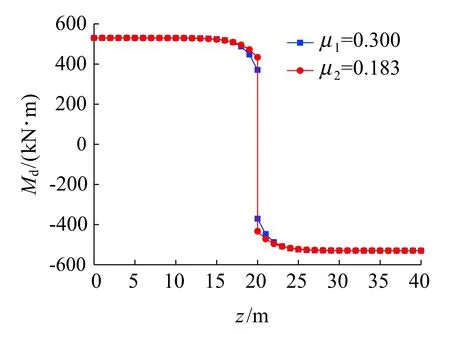
图7 简支箱梁自由扭矩分布对比
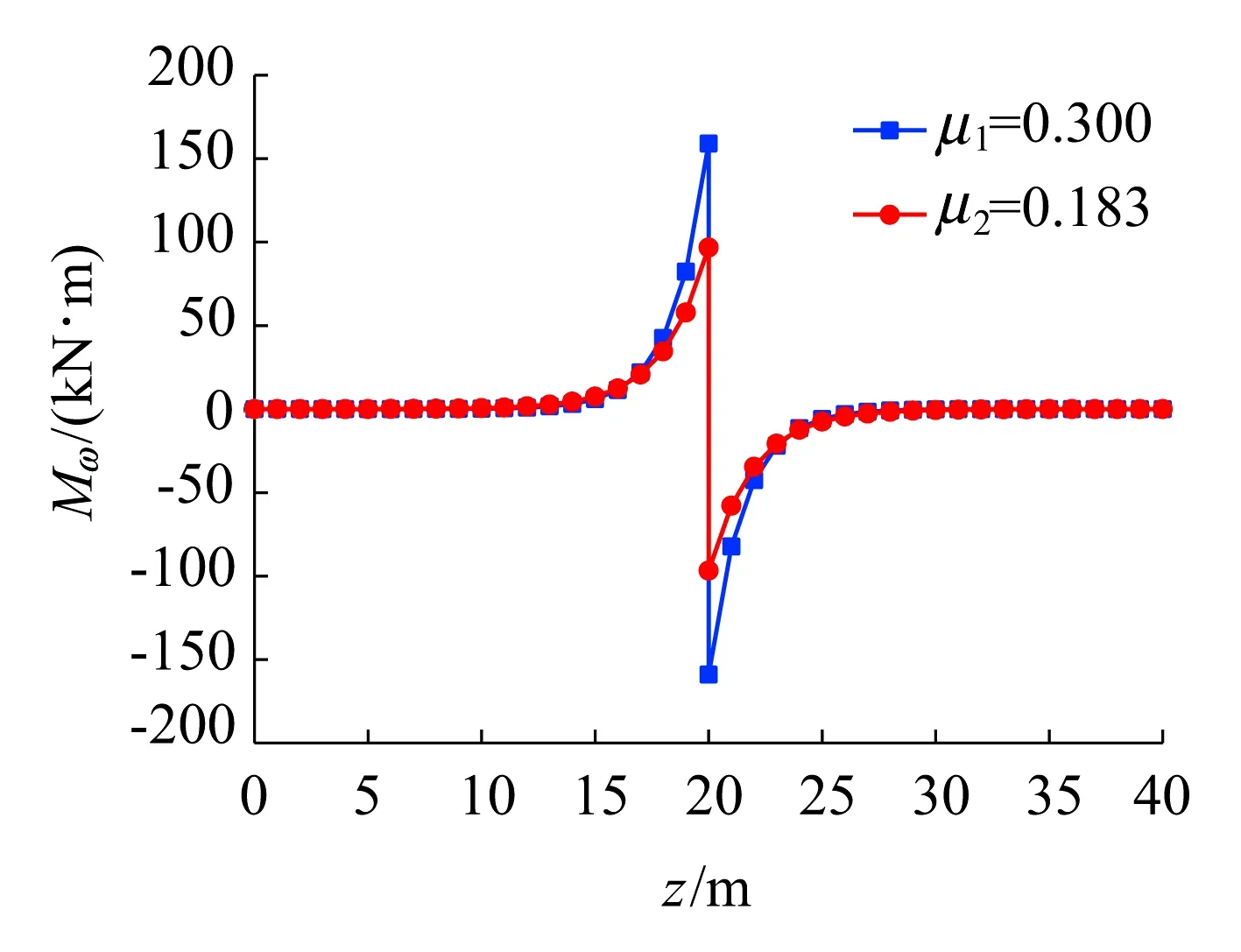
图8 简支箱梁二次扭矩分布对比
由图6~图8可知,按两种不同方法计算极惯性矩对广义内力计算结果有较大影响,尤其对跨中截面的双力矩和二次扭矩有明显影响。
4 结论
(1)本文从分析薄壁箱梁横截面上剪应力合成的扭矩出发,提出极惯性矩的合理计算方法,明确了计算带悬臂板箱梁截面的极惯性矩时应考虑悬臂板的影响。
(2)选取跨中作用集中扭矩荷载的简支箱梁算例,将约束扭转解析理论与有限元软件ANSYS壳单元计算的横截面翘曲正应力进行比较,结果表明,按照全截面计算极惯性矩和相应翘曲系数时求得的翘曲正应力与ANSYS壳单元的计算结果更加吻合,进一步验证了考虑悬臂板的合理性。
(3)对于跨中作用集中扭矩荷载的简支箱梁,按全截面或仅按闭口截面计算极惯性矩和翘曲系数对扭转角和广义翘曲位移影响较小,但对双力矩和二次扭矩等内力有明显影响,只按闭口部分计算极惯性矩时将大幅低估箱梁跨中截面的双力矩和二次扭矩。
(4)简支箱梁承受集中扭矩荷载时的双力矩和二次扭矩都具有快速衰减的分布特性,其只对加载截面及其附近截面的应力分布有明显影响,其余梁段内的总扭矩仅为自由扭矩。

