基于管状导体模型钢轨高频频变参数计算

彭 涛，陈剑云

(华东交通大学 电气与自动化工程学院，江西 南昌 330013)

钢轨在牵引供电中承担牵引回流和传输信号的作用同时，还传输丰富的行波信号[1-2]。而钢轨的电感L和电阻R参数会随频率发生变化(简称频变参数)。钢轨的参数频变现象会导致行波在其传播过程中产生色散，所以在研究故障行波在钢轨中传播特性时，钢轨的频变参数特性不可忽视[3-5]。为了对后续故障行波色散研究提供数据基础，本文主要针对钢轨频变参数计算展开研究。

钢轨铁磁材料特性和“工”字形不规则截面[6]，导致目前并没有很好的办法确定钢轨的频变参数。对于一般不规则导体频变参数计算，目前主要的方法有等效管状数学模型和有限元软件仿真等方法[7-8]。管状导体模型[9]是一种针对不规则导体计算频变参数的常用方法，将不规则导体等效成管状模型，直接采用数值计算方法计算导体频变参数特性，数学模型精度较高，易于编程。但是在计算过程中难以确定导体的等效管状模型内径、外径等参数，较为复杂。文献[10-12]提出将钢轨等效为管状导体计算钢轨频变参数。其中文献[10]提出一种四参数等效管状模型计算钢轨频变参数，但是需要同时需要确定四种参数，较为复杂。文献[12]讨论了通过建模导体细分方法来确定钢轨等效管状模型下各计算参数的确定，无法直接用数值计算方法进行计算。

有限元建模仿真计算不规则界面导体频变参数另一个普遍的方法是通过偏微分方程边值问题以及大量的网格划分解决通过磁场、电场的不规则界面导体内阻抗计算。文献[13-15]利用FEM有限元分析软件对钢轨的频变参数进行研究，并取得了一定的效果。

现有针对计算钢轨频变参数方法，计算模型需要确定参数较多，较为复杂。本文根据已有管状导体计算模型，针对计算钢轨高频频变参数要求，对管状导体模型进行了简化，并给出了简化管状导体中各计算参数的确定方法，利用简化管状导体数学模型对钢轨频变参数进行计算。

1 管状导线模型

1.1 管状导线模型基本原理

在交变电流的作用下，导线和大地中会出现集肤效应，使输电线路的电阻和电感成为电流、频率的参数，简称频变参数，这使得计算线路阻抗十分复杂。考虑集肤效应时，频变参数的主要影响是导线的自阻抗。在计算一般圆形导体时，为了计算的方便，我们一般采用管状导线模型来计算导线的自阻抗，它既可以计算管状导线，又能用来作为钢芯铝线等导线，是管状导线内径为零的特例。管状模型时导线内阻抗可以表示为[9]

(1)

(2)

但是钢轨作为一种不规则导体，其横截面为“工”字形。很难有有效的数学模型计算钢轨的内阻抗。文献[10]提出一种将钢轨等效为管状导体模型的方法来计算钢轨内阻抗，如图1所示。

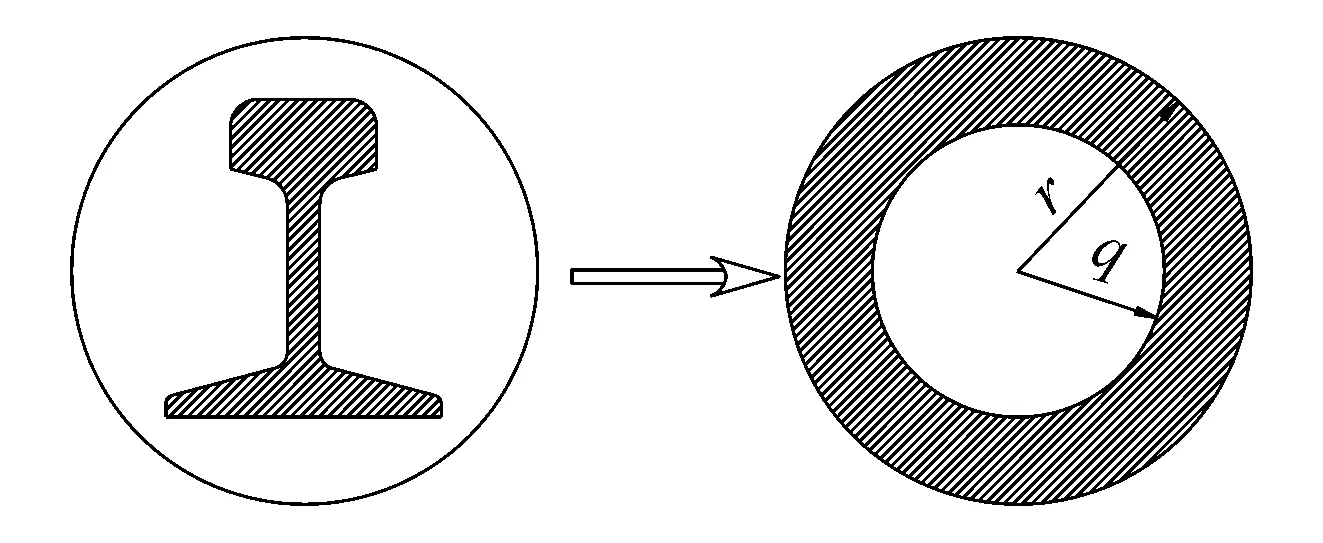
图1 钢轨等效管状导线示意图

根据式(1)和式(2)可知，钢轨管状导线模型需要确定3个关键参数：钢轨等效管状模型磁导率μ；等效管状导线模型外径r；等效管状导线模型内径q。

1.2 钢轨等效管状导体模型的简化

在大量的计算仿真过程中，发现在高频状态下，利用管状等效导体数学模型计算不规则导体频变参数时，管状导体模型内径q对结果几乎无影响。通过验证这一结果，给出一种简化的钢轨等效管状导体模型。

崔：既然提到了“拉三”，那么这几个经典版本的“拉三”，哪个是您的最爱？是拉赫玛尼诺夫本人的经典演绎？是霍洛维兹的传承和创新？是阿格里奇的极致炫技？还是范·克莱本在“柴科夫斯基国际钢琴比赛”中对此曲的解构与重塑？

在讨论内径q对结果的影响时，对相对磁导率、外径r取固定值，测试不同频率下内径q数值上的变化对钢轨内阻抗的计算结果影响，见表1。在本次验证过程中，对钢轨等效管状模型其他参数采用固定值，内径q从0.005 4按照步长0.001自增，观察每自增一次最终结果的变化。

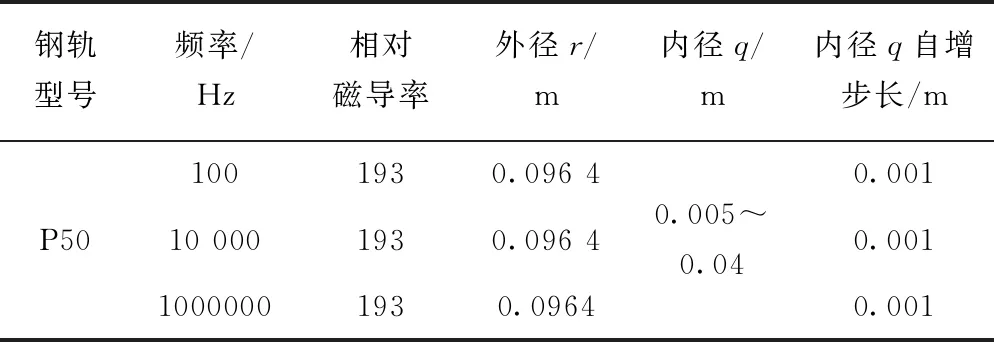
表1 内径q对最终结果影响实验各参数取值

表2为不同频率下内径变化后的计算结果。根据表2计算结果可知，当频率为100以上时，内径q对计算结果几乎没有影响。分析其原因，频变参数主要是集肤效应的影响，在高频情况下，钢轨内阻抗主要集中在钢轨表面，所以等效模型中内径q在高频情况下对计算结果几乎无影响。在研究钢轨频变参数对行波色散的影响时，考虑到行波的高频特性，可以忽略内径q的影响，即将管状导线模型近似等效为实心导体。

(3)

(4)

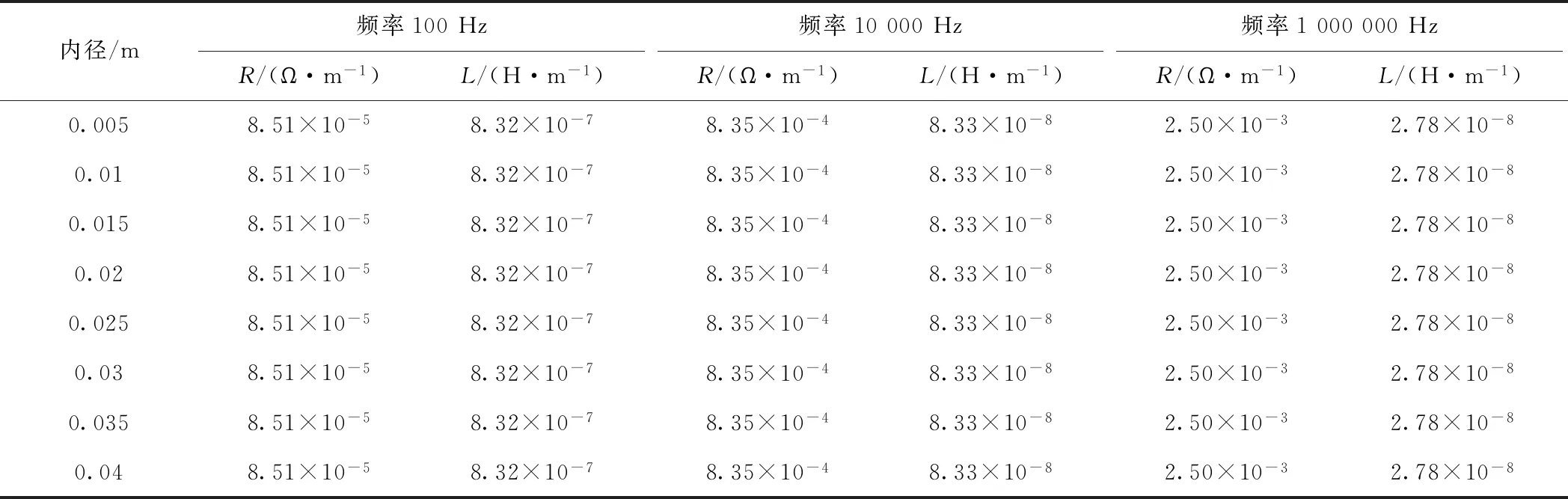
表2 不同频率下内径变化后的计算结果

(5)

根据式(5)可知，简化模型只需要确定两个关键参数：钢轨等效管状模型磁导率μ；钢轨等效管状模型外径r。

2 钢轨等效管状导体模型参数的确定

2.1 钢轨等效管状模型磁导率μ确定

为计算方便，把不同磁介质中的磁导率μ与真空中的磁导率μ0进行比较，比较的倍数用μr表示，叫做相对磁导率。相对磁导率是一个常数。

μr=B/(μ0H)

(6)

(7)

式中：μ0为真空磁导率，一般认为μ0=4π×10-7H/km；μr为相对磁导率；I为钢轨电流；P为钢轨截面周长。

在采用管状导体模型计算钢轨频变参数时，由于模型进行了等效转换，不能直接使用钢轨相对磁导率代入等效管状模型进行计算，而应该使用一个具有某种平均意义的有效磁导率μe[16]。而在直流情况下，管状导体直流内感Lint(dc)可以表示为

(8)

(9)

当利用钢轨等效管状简化模型时，由于S=0，g(S)=1，有

μe=Lint(dc)·8π

(10)

式中：Lint(dc)可现场测量获取，亦可有限元仿真直流情况下钢轨内感获得。本文采用有限元分析软件Anasys-Maxwell对P50型号钢轨有限元建模仿真获取Lint(dc)，在实际工程中，还需要对钢轨直流情况下内感进行测量，以尽量消除误差。

2.2 钢轨等效模型外径r的确定

根据文献[2]定义自阻抗

Z=jωLii+Zc+Zg

(11)

Zc=Rc+jωLc

(12)

Z0是导线的内电阻，根据文献[3]，在忽略Zg的前提下，定义钢轨的自阻抗为

Zc=Zext+Zin

(13)

Zext=jωLii

(14)

(15)

由于Zin与频率和导体电流分布有关，在频率f→∞时，电流集中在导体的表面，Zin→0。在管状导线模型中，此时导体阻抗主要由外径决定，在非常高的频率下，导体阻抗与内径q无关。

(16)

(17)

此时r=ri，在能够获取到极限高频率下钢轨自阻抗时，可以根据式(17)确定钢轨的等效管状导线外径r。一般情况下，我们可以用有限元分析软件仿真极限频率获取钢轨极限频率下的钢轨自阻抗。

本文采用有限元分析软件Anasys-Maxwell对P50型号钢轨[17]1∶1有限元建模仿真，可以得到极限频率f∞下钢轨的自阻抗参数(取极限频率f∞=107Hz)，见表3。

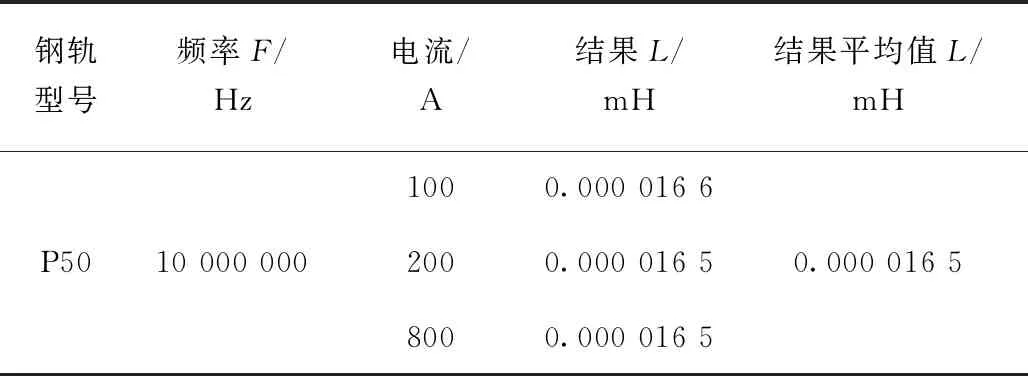
表3 有限元仿真极限频率下P50钢轨自阻抗

根据表3仿真结果电感L的平均值以及式(17)，得到P50型号钢轨等效管状模型外径r数据。

3 算例计算

根据第二章确定的相对磁导率μ和外径r，利用管状导体模型对P50钢轨进行算例计算，其取值参数见表4。

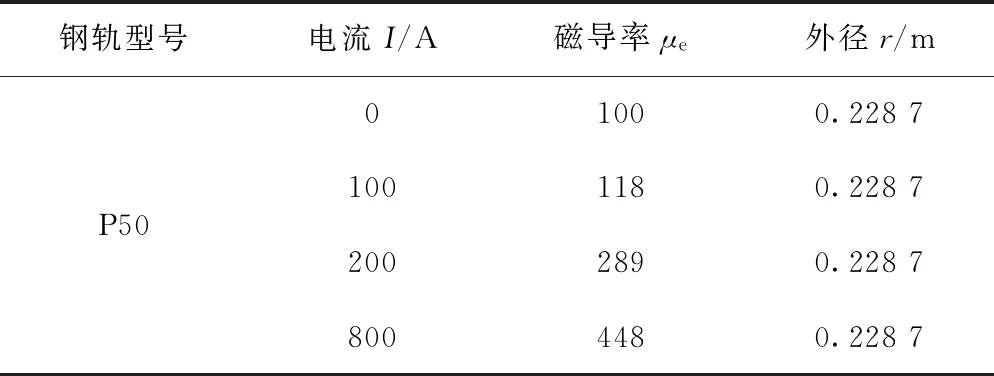
表4 简化管状模型计算参数

利用表4参数，根据简化管状导体模型对P50型号钢轨频变参数进行计算，分别计算在0～10 000 Hz频率下电流为100、200、800 A钢轨频变参数数据，见表5、表6。

表5 简化管状模型计算钢轨电阻R

表6 简化管状模型计算钢轨电感L

图2为P50钢轨电流为100、200、800 A三种情况下不同频率下的电阻R的变化曲线，图3为P50钢轨电流为100、200、800 A三种情况下不同频率下的电阻L的变化曲线，表5和表6分别为其中截取的部分计算结果数据。由图2、图3和表5、表6数据分析可知，钢轨电阻R随着频率增加不断增大，电感L随着频率增加逐渐减少，最后趋于稳定。总体而言，钢轨频变参数中R、L随频率变化明显，当行波在钢轨传播过程中，不同频率成分的行波分量具有不同的波速度和衰减系数。在研究行波故障测距考虑行波色散过程中，钢轨频变参数对其影响十分巨大，对此进行深入的基础性研究非常必要。

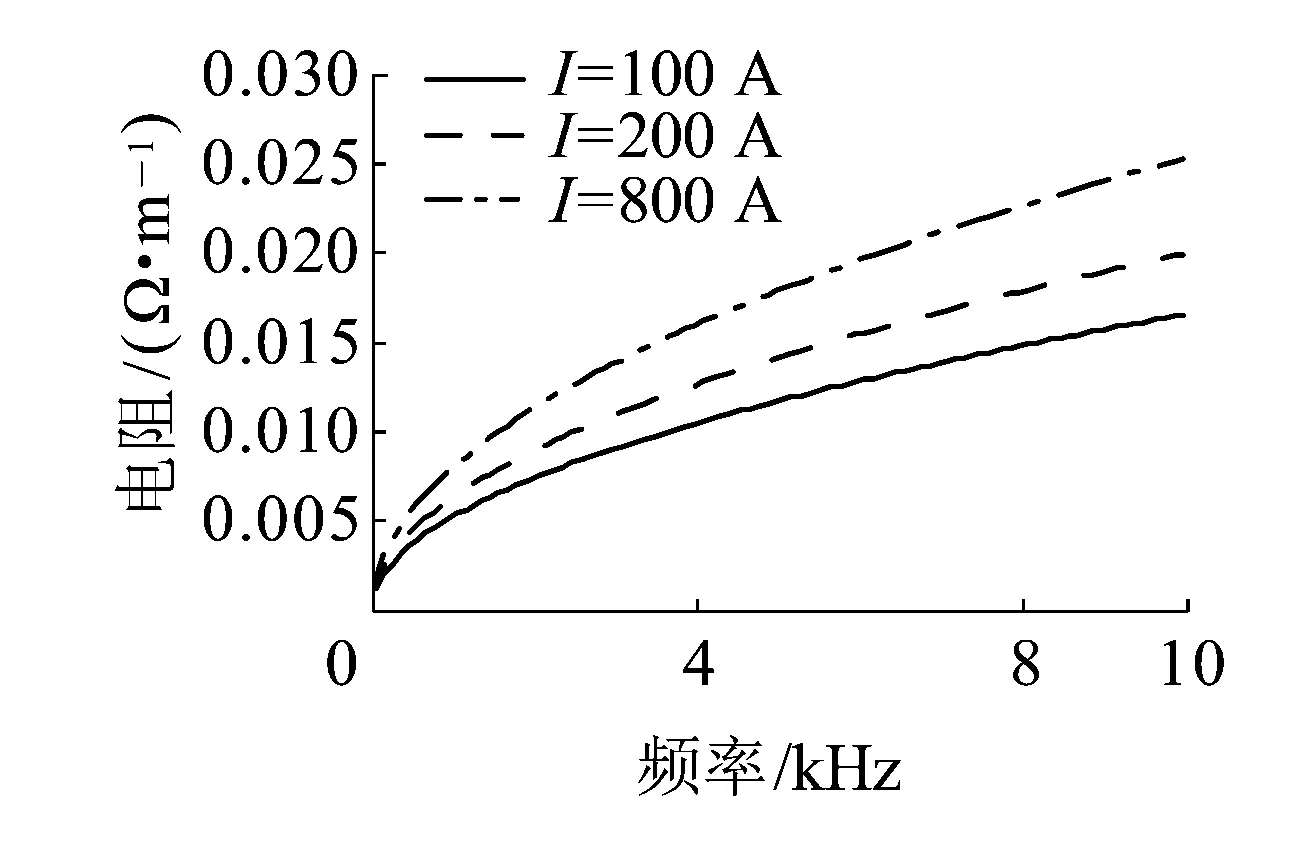
图2 简化管状模型计算P50钢轨电阻R

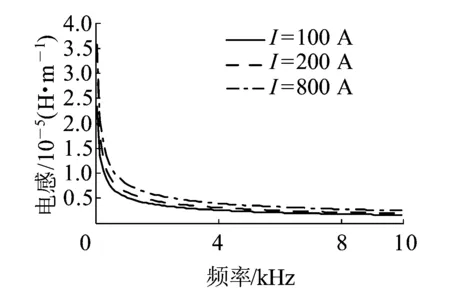
图3 简化管状模型计算P50钢轨电感L

4 结束语

本文根据现有管状导体计算模型，得到一种针对计算钢轨高频频变参数的简化等效管状数学模型，对简化数学模型中各参数的确定给出详细确定方案，并通过MATLAB语言实现该模型计算过程，利用该简化模型对P50钢轨频变参数进行计算，计算结果为后续研究牵引供电系统行波故障测距中行波色散问题提供基础数据参考。从计算结果分析可知，钢轨频变参数中R、L随频率变化明显，在考虑行波色散过程中，钢轨频变参数对其影响十分巨大，不可忽略。但是在计算过程中，钢轨等效管状模型磁导率μ很大程度依赖有限元仿真直流内感Lint(dc)的准确性。后续将对钢轨相对磁导率μ的确定进行深入研究。