Advanced Frozen Permeability Technique and Applications in Developing High Performance Electrical Machines

Zhu Z Q Chu W Q



Advanced Frozen Permeability Technique and Applications in Developing High Performance Electrical Machines

（University of Sheffield Sheffield S1 3JD U.K.）

Magnetic saturation is one of the major challenges for all electrical machines and makes it much more difficult to design high performance electrical machines. Frozen permeability (FP) technique has recently been developed to predict the on-load components of electromagnetic qualities while considering the influence of magnetic saturation. In this paper, the FP technique and its applications in various electrical machines are comprehensively reviewed. It shows that the FP technique is able to accurately separate on-load magnetic field, flux linkage, and inductance components in all types of electrical machines. These on-load field components and parameters can be further utilized to investigate various on-load performance, such as on-load torque and torque ripple components, on-load back EMFs and voltages, flux weakening performance, radial force distribution, et al. The accurate on-load parameters can also be used to improve the machine models and controls. Hence, FP technique provides a holistic approach to the development of high performance electrical machines.

Electrical machines, frozen permeability, on-load performance, permanent magnet

0 Introduction

Due to global energy security and environmental concerns, significant efforts have been made on exploiting renewable and sustainable resources of energy, such as wind power, solar power, and tidal power, etc. Electrical machines and drives represent one of the key enabling technologies for exploiting these energy resources. Meanwhile, electrical drives also exhibit the advantages of high efficiency, fast response and accuracy. These advantages coupled with recent advances in computational capabilities and power electronics have accelerated the pace of replacing conventional mechanical, hydraulic, or pneumatic propulsion and transmission systems by electrical systems for various applications[1-4].

In electric drive systems, the system performance largely depends on the electrical machines employed. Progress in the materials, power electronics, and control technologies over the past few decades has enabled the developments of various electrical machines[1-12]. The major electrical machine techno- logies are summarized in Fig.1. Historically, electric drives were dominated by induction machines (IM) and electrically excited (EE) machines. However, more recently, new machine technologies such as permanent magnet (PM) machines have become more popular due to high torque density and efficiency, especially when high energy rare-earth permanent magnet materials are employed. Switched reluctance (SR) and synchronous reluctance machines are developed by utilizing reluctance torque. The torque densities of reluctance machines are similar to IM's and hence reluctance machines are usually considered as alternative options to IMs, albeit with a low power factor. However, electronic controllers are inevitably required to operate reluctance machines. Hybrid electrical machines are developed by uniquely integrating different machine technologies. Due to the variety ways of integration, a large number of hybrid electrical machines have been developed and are one of the most popular research topics under investi- gation[12].

Despite of variety technologies, one of the major challenges for all electrical machines is the magnetic saturation. This is due to the nature of nonlinear soft magnetic materials. The magnetic saturation affects nearly all aspects of electrical machines, such as magnetic field distributions, flux linkages, voltages, average torque and torque ripple, overload capability, inductances, flux weakening capability, torque speed curve, iron losses and efficiency. More importantly, the magnetic saturation makes it much more difficult to predict the breakdown contributions and/or components of aforementioned performances. However, in order to develop high performance electrical machines, it will be greatly helpful to reveal the relationships between the design parameters and the breakdown contributions/components of aforemen- tioned performance under different loadings.

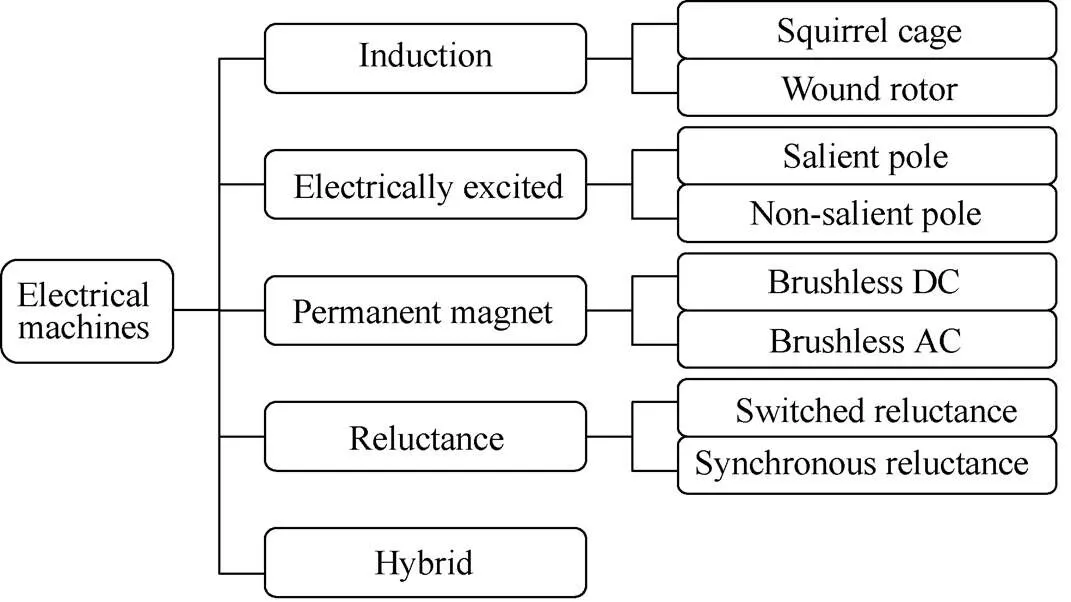
(a) Classification

(b) Induction (c) Electrically excited

(d) Permanent magnet (e) Switched relectance

(f) Synchronous reluctance (g) Hybrid

Fig.1 Classification and cross-sections of different electrical machines

On the other hand, with the progress of finite element software, frozen permeability (FP) technique has been developed and becomes available in the commercial software. The FP technique is able to calculate the electromagnetic qualities while con- sidering the influence of magnetic saturation and hence widely used to investigate the issues related with magnetic saturation. Thus, it can provide strong technical supports on developing high performance electrical machines.

In this paper, the advanced FP technique and its applications in various electrical machines are comprehensively reviewed. The principle of FP technique is described in section 1. The sections 2～9 are devoted to the applications of FP technique on different topics of PM machines, such as on-load magnetic field, flux linkages and inductance estimation, separation of torque components, on-load cogging torque, on-load torque ripple, on-load back EMF, on-load voltage waveforms, flux weakening et al. The applications of FP technique to other technical issues and other types of electrical machines are highlighted in sections 10 and 11.

1 Principle of Frozen Permeability

The early publications on FP technique can be found in Ref.[13-16]. Currently, FP technique has been widely used in all types of electrical machines to investigate the issues related with magnetic saturation and cross-coupling as will be shown later. Taking PM machines as an example, the principle of FP technique is illustrated in Fig.2.

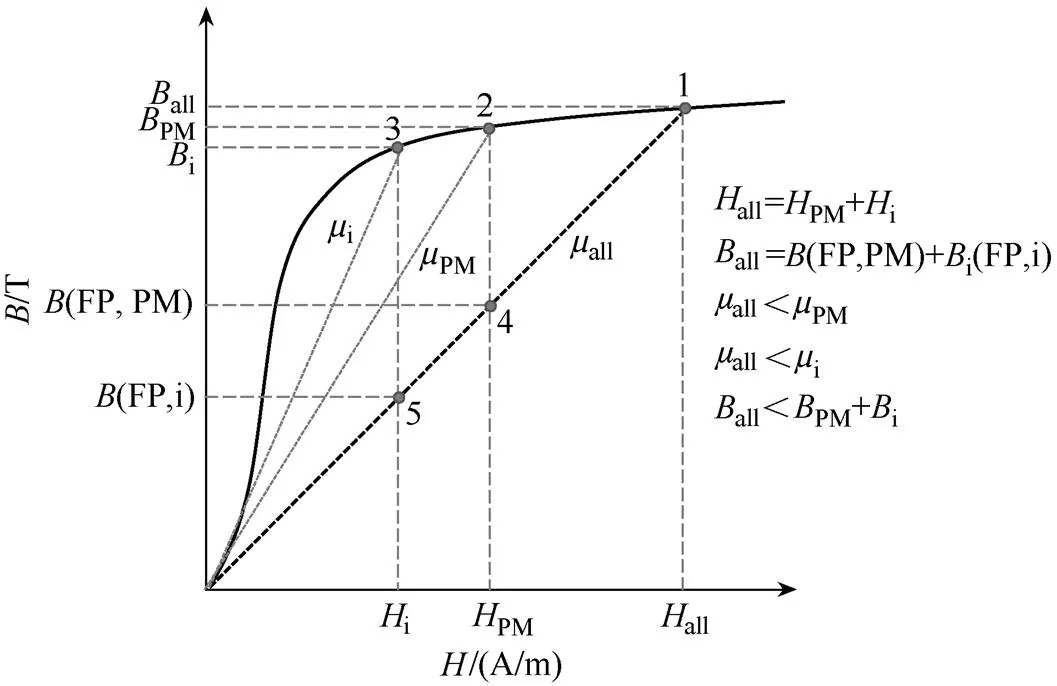
Fig.2 Principle of frozen permeability technique

When a PM machine is on load, the machine is excited by both the PM and the armature current. The resultant operating point can be presented by point 1 (allandall). It is well known that due to nonlinear-curve of soft magnetic material, althoughall=PM+i,all≠PM+i, wherePMrepresents the resultant flux density with the PM excitation (PM) only (point 2) andirepresents the resultant flux density with the armature excitation (i) only (point 3). Therefore, the on-load field components due to PM and armature cannot be accurately decomposed by using conventional calculations with the PM or armature excitation only.

The FP technique is based on the fact that all excitations always share the same permeability distribution when electrical machines are on load. Hence, the on-load permeabilityallis obtained and stored by solving the on-load model (point 1). Then, two linear analyses represented by the points 4 and 5 are solved further based on the frozenallwith either the PM or armature excitation only to obtain(FP,PM) or(FPi), respectively. Since all three calculations are based on the same permeability (all),all=(FP,PM)+(FP,i). Therefore, the on-load PM and armature field components are decomposed. Further- more, sinceallvaries with the load conditions, the influence of magnetic saturation and cross-coupling has been inherently taken into account.

Based on the principle of FP technique, its procedure can be summarized in Fig.3. Firstly, the nonlinear calculation with all excitations, referred as the whole model, is solved. Secondly, the permea- bility of the whole model, referred as the on-load permeability, in each element and at every rotor position is saved and frozen. Finally, linear calcula- tions are conducted based on the on-load permeability to obtain the on-load magnetic field components of the selected excitations.

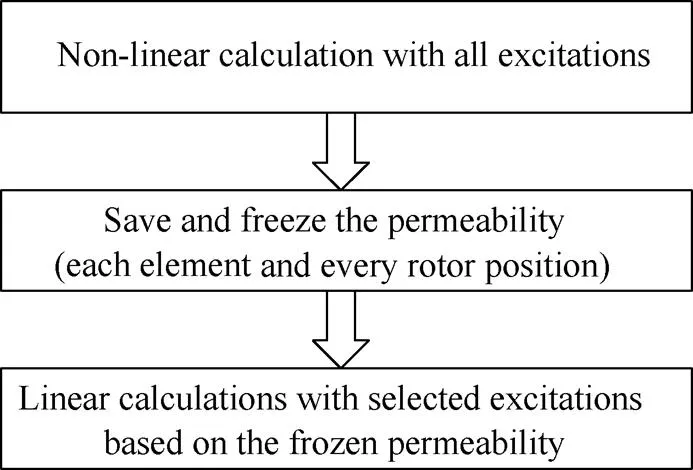
Fig.3 Procedure of frozen permeability technique

Although the illustration in Fig.2 is based on a PM machine, the FP technique is applicable to all types of electrical machines. Also the selected excitations for the linear calculations can be tailored according to investigated topics. For example, to obtain the on-load PM or armature magnetic field component in PM machines, only the PM or armature excitation is applied in the linear calculation[13,16]. To study the cross-coupling inductances between the d- and q-axes in PM machines, only the d- or q-axis current is applied[13,16]. To investigate the mutual coupling between phases in SR machines, only one phase current is applied[17].

The major challenge for the FP technique is the experimental validation, since the exact quantities that are calculated in the FP technique cannot be measured directly. Although it is tried in Ref.[18], various further work on experimental validation needs to be done. However, on the other hand, the FP technique has been widely accepted based on the fundamental magnetic circuit theory and used for on-load magnetic field separation and parameter predictions in various types of electrical machines.

In following sections, the applications of the FP technique are comprehensively reviewed. Since the most of the applications are on different technical topics of PM machines, only one of following sections is focused on the applications on the other types of machines and will presented at the end. For the rest sections, the publications are grouped according to different research topics, such as on-load magnetic field separation, on-load flux linkages and inductance calculation, torque component separation, et al.

2 On-Load Magnetic Field Separation

On-load magnetic field separation is the basic purpose of the FP technique and the foundation for all further investigations. Nearly all investigations using FP technique involve the on-load magnetic field separation, although the on-load magnetic field results may not be presented.

Fig.4 and Fig.5 show the on-load magnetic field components of an inset PM machines presented in Ref.[19] as an example. The peak phase currentais 4A, the current phase advance angle to the positive q-axis0°and the rotor positionis 0°(electrical). The main parameters of the inset PM machine are listed in Tab.1. It can be seen that the on-load magnetic field and permeability distributions in Fig.4 are neither symmetrical with the d-axis nor with the q-axis. This is due to the influence of armature field. Consequently, the on-load PM magnetic field with the PM excitation on the d-axis has the net q-axis flux linkage. The q-axis current also produces net d-axis flux linkage. Fig.5 shows the radial and tangential flux density components along the middle of the airgap in Fig.4 to illustrate the on-load magnetic flux density separation. It shows that for each sample point, the flux density in the whole model is the same as the mathematic summation of the two flux density components produced with either on-load PM or armature field only. This is also true for any other rotor position and load condition. Hence, the on-load magnetic field components can be successfully separated while the influence of magnetic saturation and cross-coupling has been taken into account.

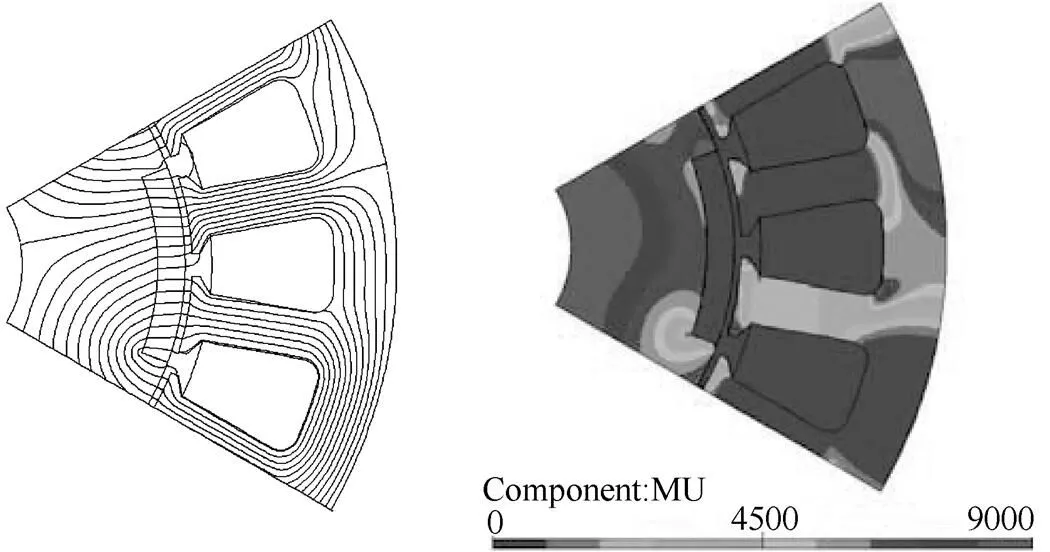
(a) Whole field (PM and current) (b) On-load permeability

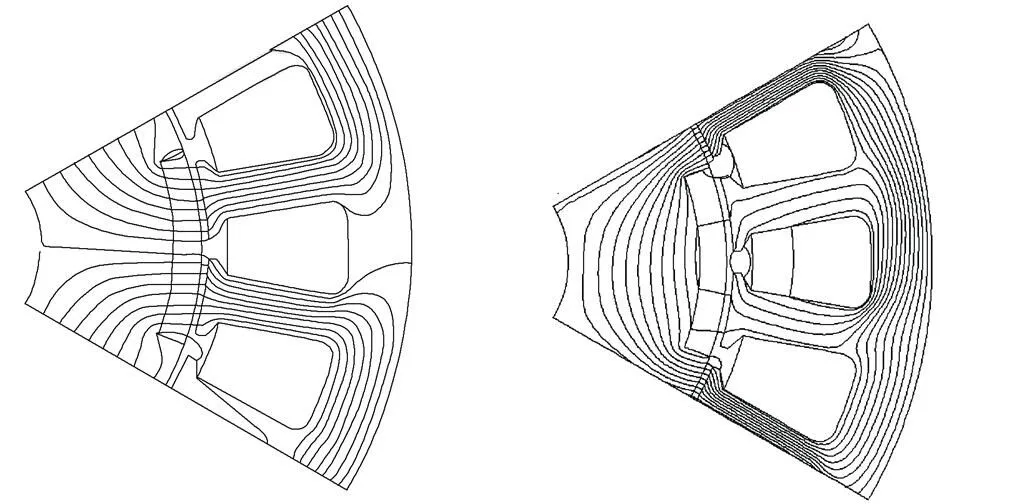
(c) On-load PM field (FP) (d) On-load armature field (FP)

Fig.4 On-load field distributions of inset PM machine when Ia=4A, =0° and =0°[19]

(a) Radial flux density components

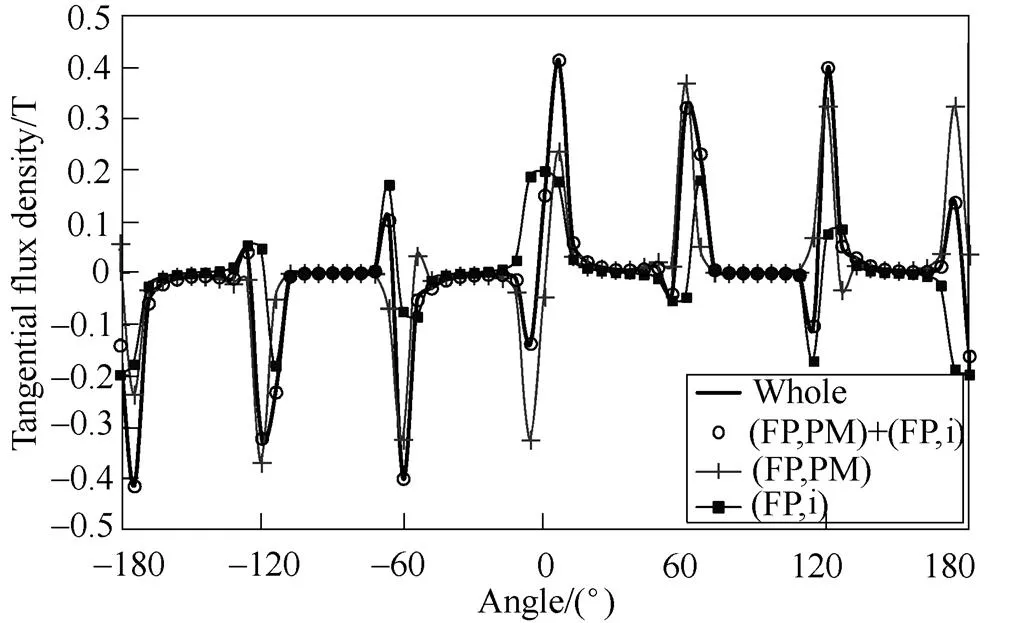
(b) Tangential flux density components

Fig.5 Flux density components at middle of airgap of inset PM machine when Ia=4A, =0°and =0°[19]

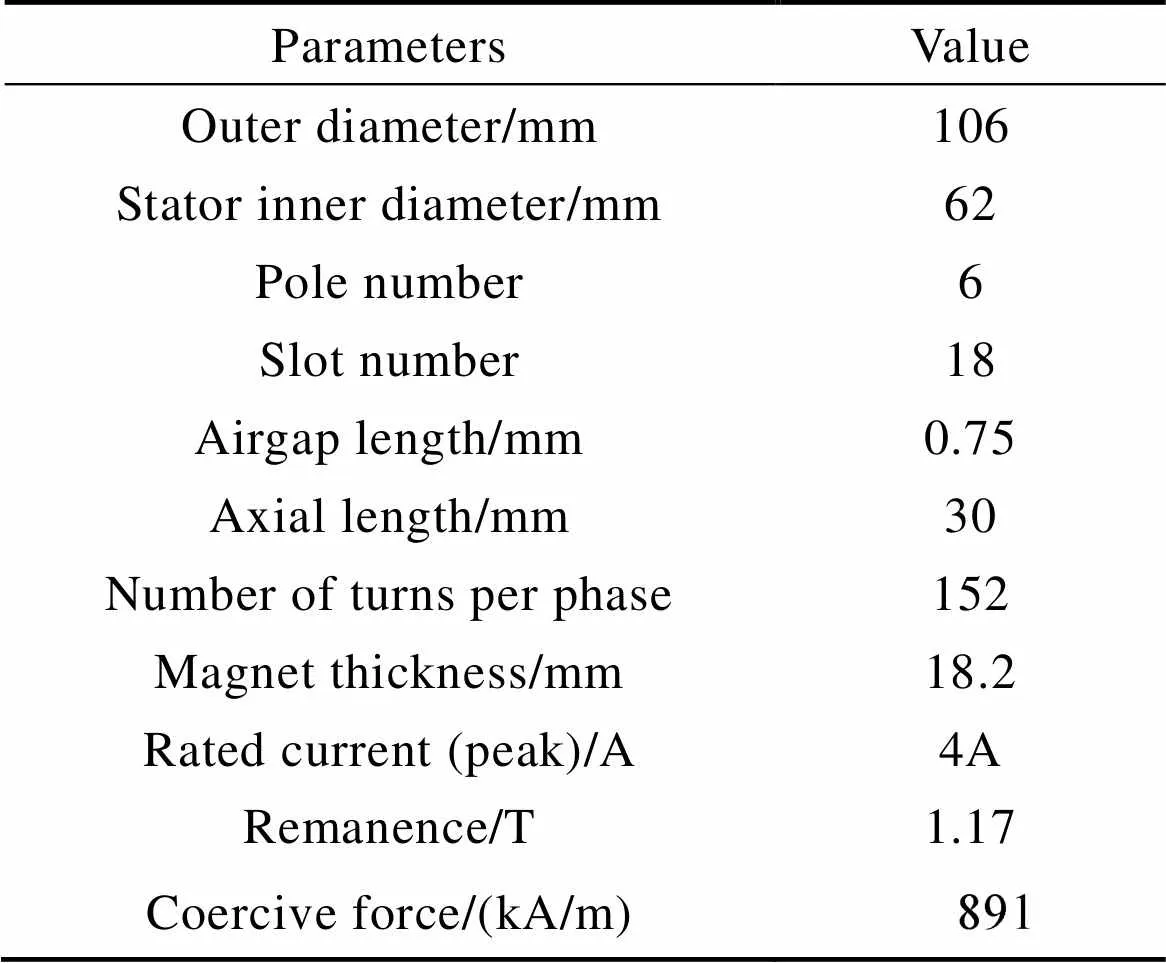
Tab.1 Main parameters of inset PM machine in Ref.[19]

Other examples of separated on-load magnetic field distributions and flux densities in PM machines can be found in Ref.[20-34]. In Ref.[20], the on-load PM and armature magnetic field distributions and airgap flux densities in a large power linear PM machines are obtained to explain the reduction of trust force density. In Ref.[23], the on-load airgap PM and armature flux density components in a surface- mounted PM (SPM) machine with eccentricity are obtained by the FP finite element analyses to validate the analytical model based on improved conformal mapping method.

Based on the on-load magnetic field separation, various on-load components of electromagnetic quantities such as flux densities and flux linkages can then be calculated for further investigations.

3 On-Load Flux Linkages and Inductances Analyses

For PM machines, the PM flux linkages and inductances are most important parameters in terms of the machine design, modelling and control. The inductances represent the armature flux linkages with the given armature currents. However, it is well known that the constant PM flux linkage and indu- ctance models may result in significant inaccuracy due to the influence of magnetic saturation. Since the FP technique is able to consider the influence of magnetic saturation, it is widely used for the calcu- lation of PM flux linkages and inductances.

In Ref.[13,16,19, 24], it has been well illustrated that the average PM flux linkage and inductances per electric cycle can significantly change with load. Consequently, they are 2D functions of both d- and q-axis armature currents (or the current amplitudeaand the phase advance angle). Furthermore, there are cross-coupling between the d- and q-axes as well as the net average q-axis PM flux linkage. Hence, the full average flux linkage model for PM machines should be expressed as

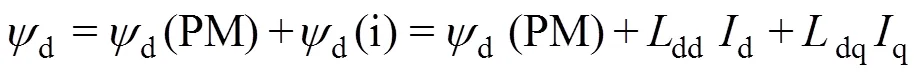
wheredandqare the total d- and q-axis flux linkages, respectively.d(PM),q(PM),d(i) andq(i) are the d- and q-axis flux linkages due to on-load PM and armature fields, respectively.dandqare the d- and q-axis currents, respectively.dd,qq, anddqare the d- and q-axis self- and mutual inductances, respectively.

Please note thatq(PM) anddqare due to the cross-coupling between d- and q-axis. Furthermore, except the variation of average values with the current amplitudeaand phase advance angle, the flux linkages and inductances also change with the rotor position. Fig.6 shows the variations of on-load flux linkages of the inset PM machine listed in Tab.1 with the rotor position whena=4A and 0° as an example. It also confirms that not only the instant- aneousq(PM) but also its average are not zero. Theaveraged(i) is also not zero, although only q-axis current is applied.

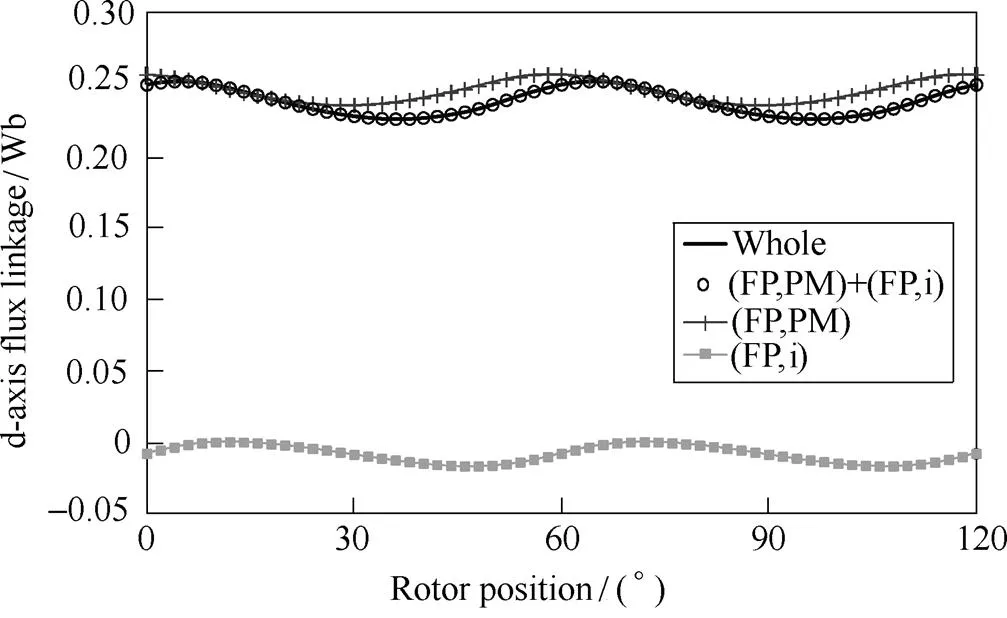
(a) d-axis flux linkages

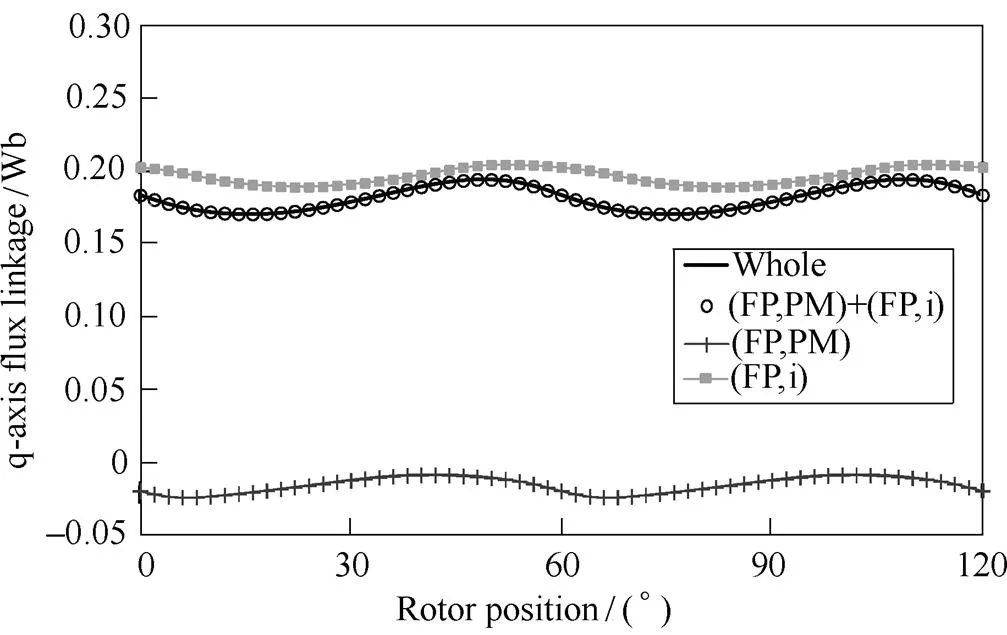
(b) q-axis flux linkages

Fig.6 Variation of flux linkages with rotor position of inset PM machine when Ia=4A and =0°[19]

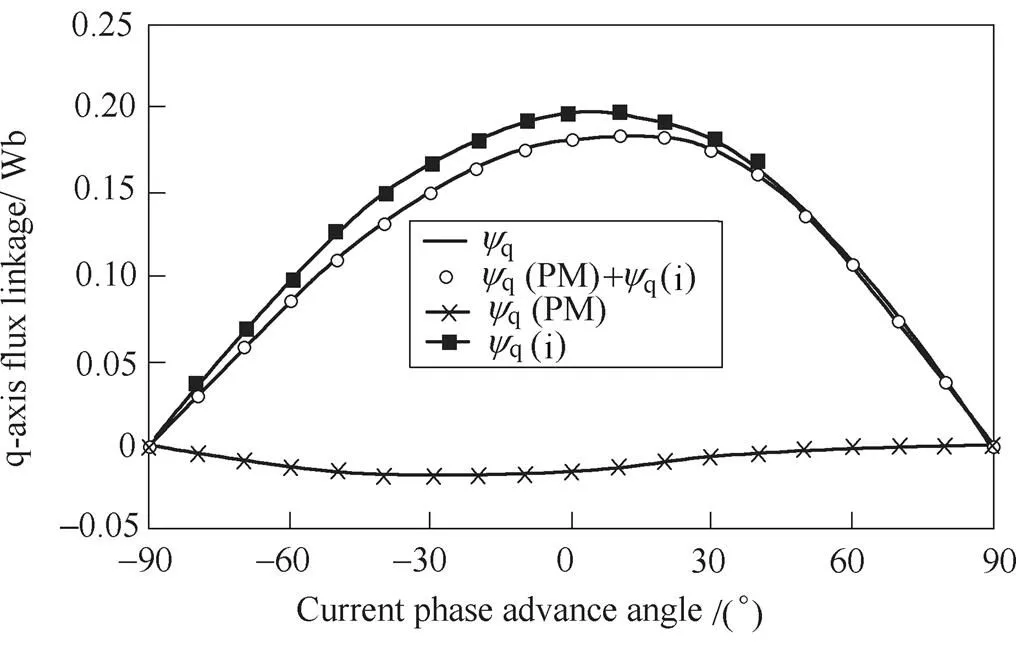
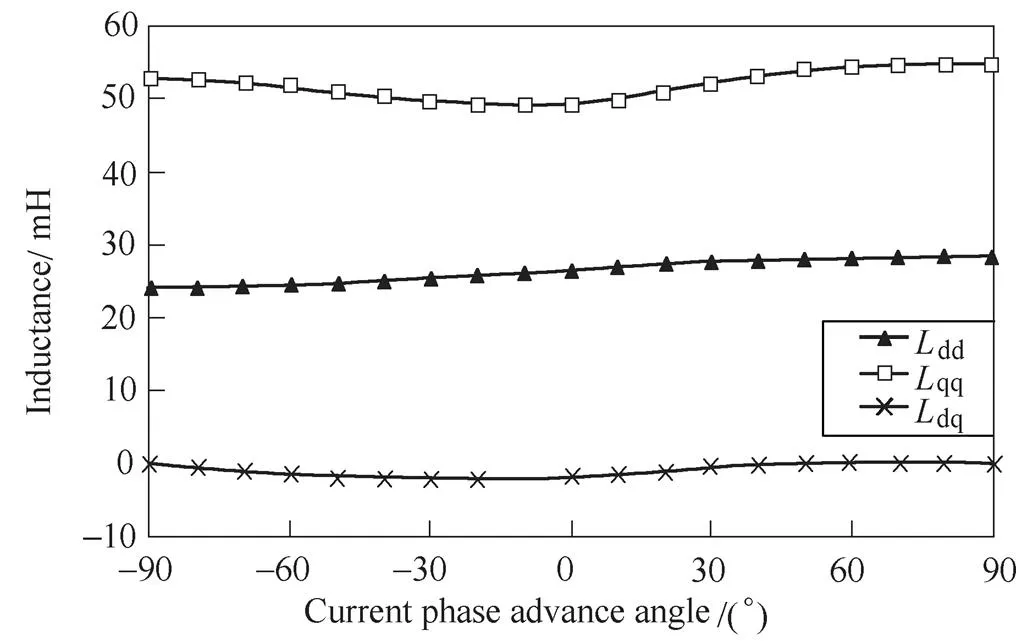
The variation of average flux linkages and inductances withis further presented in Fig.7. The influence of magnetic saturation is represented by the variation ofd(PM),dd, andqq. When=90°, the d-axis magnetic saturation is the heaviest. Hence,d(PM) andddare at their minimum. When=0°,dis zero andqis maximum. The magnetic saturation is modest along the d-axis but the heaviest along the q-axis. Therefore,d(PM) andddare higher whileqqis the lowest. When=90°,dis at the negative maximum and the magnetic saturation along the d-axis is the lowest due to the maximum flux weakening.Therefore,d(PM) andddare at the maximum. The influence of cross-coupling is represented by the variation ofq(PM) anddq. The cross-coupling is zero and henceq(PM) anddqare zero when=±90°, since all excitations are applied to the d-axis. Althoughqis maximum when=0°, the cross-coupling is the heaviest when=30°. It is due to that the cross-coupling is aggravated by the magnetic saturation.

(a) d-axis flux linkages

(b) q-axis flux linkages

(c) Inductances

Fig.7 Variation of average flux linkages and inductances of inset PM machine with  when Ia=4A[19]

Some of the other examples of on-load flux linkage and inductance calculation using FP technique can be found in Ref.[15, 24, 31]. In Ref.[15], the d- and q-axis inductances are predicted based on the combination of FP and stored magnetic energy method to improve accuracy of torque estimation in a 36-slot/4-pole (36s/4p) IPM machine. In Ref.[24], the on-load PM flux linkages and inductances are calculated for the output torque estimation of a 30s/36p inset PM machine. It shows the torque variation with the current phase advance angle can be predicted more accurately when the cross-coupling term is taken into consideration. In Ref.[25], flux linkage components are obtained for the inductances and torque components comparison between two 5-phase 20-slot fault-tolerant PM machines. One has 18-pole spoke-type rotor and the other one has 20-pole V-shape rotor. In Ref.[26], the variations of average line inductance and its ripple with the load of a 24s/4p SPM machine driven by a 6-step 3-phase BLDC inverter are calculated. The FP technique is also employed to calculate the self- and mutual inductances between different phases in a tubular permanent magnet machine with transverse flux configuration for electromagnetic launch (EML) applications in Ref.[27,28], the d- and q-axis inductances of variable-flux flux-intensifying PM machine in Ref.[29], and the d-axis flux linkage components of stator slot PM machine with doubly salient structure in Ref.[30]. In Ref.[31], the on-load PM flux linkage of double-stator flux-switching PM machine using ferrite magnet is calculated by FP technique to explain the torque deterioration due to magnetic saturation under heavy load.

4 Separation of Torque Components

Based on the flux linkage components and inductances, it is then possible to discuss the torque component separation. Before the torque component separation, it is necessary to review the torque calculation theories.

The Maxwell stress tensor and virtual work principle are two most widely used methods for torque calculation. It is well-known that these two methods are identical for torque calculation in normal FE simulations although attention should be paid to the mesh discretization[32,33]. This is also confirmed by Fig.8, which shows the instantaneous torque waveforms of the inset PM machine listed in Tab.1 whena=4.0A and=30°. The torque calculation using virtual work principle is given as

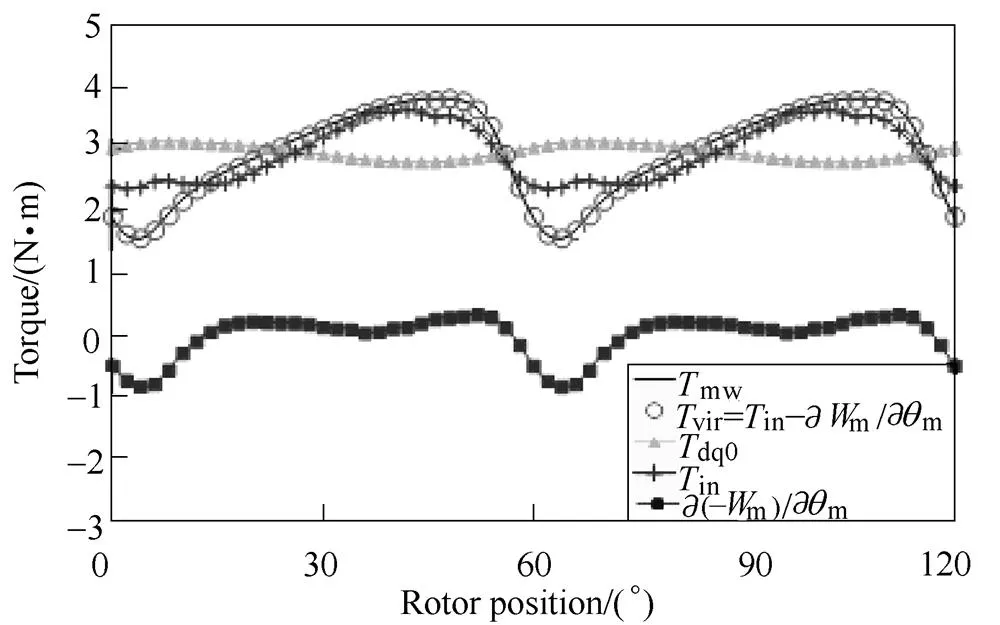
Fig.8 Torque components of inset PM machine when Ia=4.0A and b =-30°[19]

Since ∂m/∂m,d/d, andq/dhave no contribution to the average torque based on the fact that the magnetic field repeats every cycle, the average torque can also be calculated by the classical dq0 model in Equ.(5). Since Equ.(5) does not require derivative operation and the calculation of magnetic energy, it is much simpler and more widely used for torque calculation. However, it should be noted that the classical dq0 model in Equ.(5) is only able to predict the average torque but not the instantaneous torque.

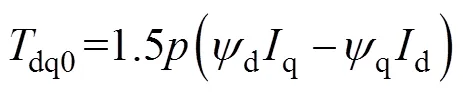
Combined with FP technique, there are two possible ways of torque component separation. One is based on the Maxwell stress tensor method[34,35]and the other one is based on the virtual work principle[13,33]. However, it is found in Ref.[33] that due to the influence of equivalent rotational magnetic saliency in the stator, a part of PM torque will be improperly attributed to the reluctance torque when the Maxwell stress tensor method is used together with the FP technique. This is eliminated by using the virtual work principle. Therefore, the on-load torque components separation should be based on the combination of virtual work principle and FP technique. Thus, the average torque com- ponents can be separated based on the flux linkage components obtained by the FP technique as

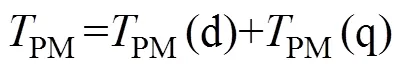
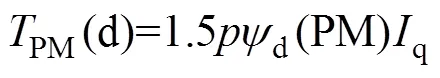
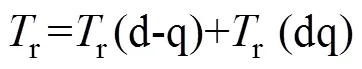
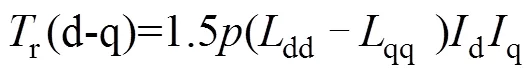
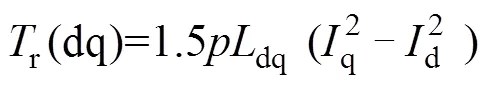
wherePM,PM(d), andPM(q) are the PM torque and its components due tod(PM) andq(PM) respe- ctively.r,r(d-q), andr(dq) are the reluctance torque and its components due to the self-inductances and mutual inductance, respectively.

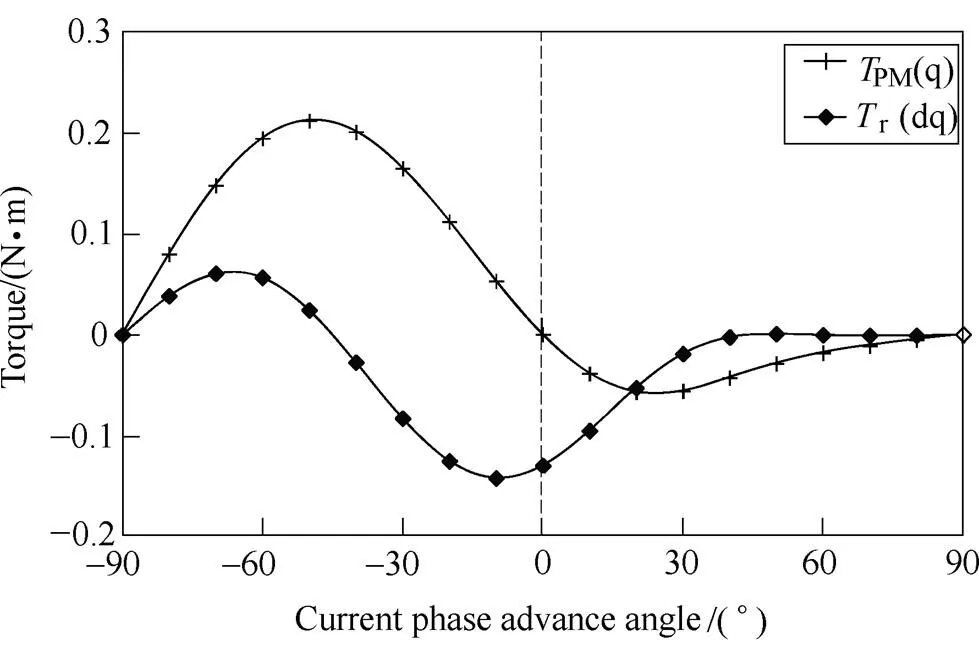
As an example, the torque component variation with the current phase advanced angle of the inset PM machine whena=4.0A is shown in Fig.9.

The average torque separation method suggested in Ref.[33] is widely accepted and used for various types of PM machines, such as 5-phase 20-slot spoke- type and V-shape fault-tolerant PM machines[25], 24s/4p SPM machine driven by a 6-step 3-phase BLDC inverter[36], 6s/4p asymmetric V-shape, surfaceinset, interior PM (IPM) machines[37-39], 12s/22p switched flux PM machine[40], 12-slot/10-pole SPM machine[41], modular linear flux reversal PM motors[42], and 12s/10p hybrid excited switched flux PM machines[43]. Although the torque component separation is also based on the flux linkage components, the torque components may be defined differently as shown in Ref.[16, 44, 45].

(a) Main torque components

(b) Torque components due to cross-coupling

Fig.9 Torque components of inset PM machine when Ia=4.0A[19]

Except the above mentioned publications, Ref.[46] suggests another possible way of torque component separation method based on the com- bination of the Maxwell stress tensor and the FP technique. Instead of two linear calculations with either PM or all armature currents, six calculations which are all possible combinations of PM,dandq, are carried out based on the on-load permeability. Then, six torque components are mathematically calculated from the six torque results of six linear analyses based on the Maxwell stress tensor. However, the improper torque attribution due to the influence of equivalent rotational magnetic saliency in the stator remains.

5 On-load Cogging Torque Analyses

For PM machines, cogging torque is another widely investigated topic. The cogging torque is produced by the interaction between the rotor PM and the stator magnetic reluctance variation. It is merely a pulsating torque and has no contribution to the average torque. For the open-circuit cogging torque, it can be calculated either by the Maxwell stress tensor and the virtual work principle as

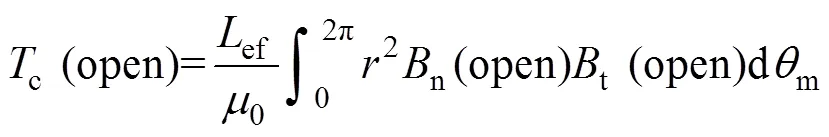
where0is the permeability of free air space.efis the effective axial length.is the radius of integration path.n(open) andt(open) are the normal and tangential airgap flux density components on open-circuit, respectively.

For the on-load cogging torque, several calculation methods are suggested by analog with the open-circuit ones in Equ.(12) and Equ.(13). By analog with Equ.(12), the on-load cogging torque in Ref.[22, 34,35] is computed as

wheremw(FP, PM) is the calculated torque based on the Maxwell stress tensor with on-load PM field only.n(FP, PM) andt(FP, PM) are the normal and tangential airgap flux density components due to the on-load PM field only.

Being analog with Equ.(13), it is mentioned in Ref.[47] that the on-load cogging torque can be calculated as the derivative of the total magnetic energy with respect to the rotor position at constant current

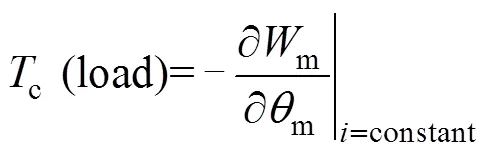
However, it is inappropriate since the total magnetic energy is also contributed by the armature field when the machine is on load.

In Ref.[34], the on-load cogging torque is calculated in a slightly different way as

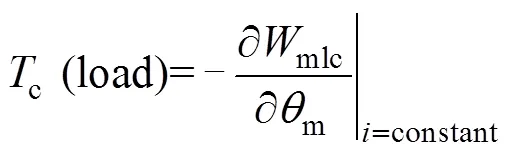
wheremlcis the magnetic energy stored in the system less the magnetic energy stored in the coils and includes components as airgap, magnets, rotor and stator steel and any other motor regions, which are not parts of the coils.

However, without using the FP method, tech- nically, it is impossible to separate the magnetic energy due to the armature field, since the on-load PM and armature fields exist in every region and are coupled each other. Hence, it is also inappropriate.

In Ref.[48], an improved FP technique is suggested to calculate the on-load cogging torque based on the on-load PM field magnetic energy derivation using Equ.(17). This method is also used later in Ref.[40].

wherem(FP, PM) is the total magnetic energy with on-load PM field only.

Fig.10 compares the torque results calculated by Equ.(14) and Equ.(17) of the inset PM machine listedin Tab.1. It shows thatmw(FP,PM) has non-zero average torque and hence cannot be exactly the on-load cogging torque. This is due to the improper torque attribution caused by the equivalent rotating magnetic saliency in the stator[33,48]. By using Equ.(17), the improper torque attribution is inherently eliminated while the influence of electric load and magnetic saturation is still fully included. Hence, the on-load cogging torque can still be obtained properly and shown in Fig.10b.

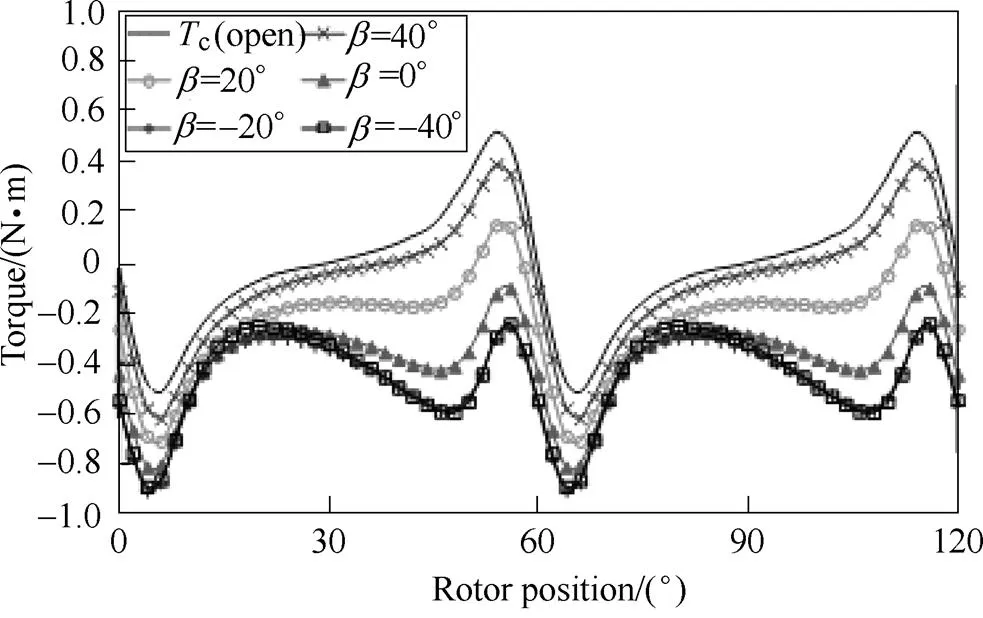
(a) By Equ.(14) based on Maxwell stress tensor

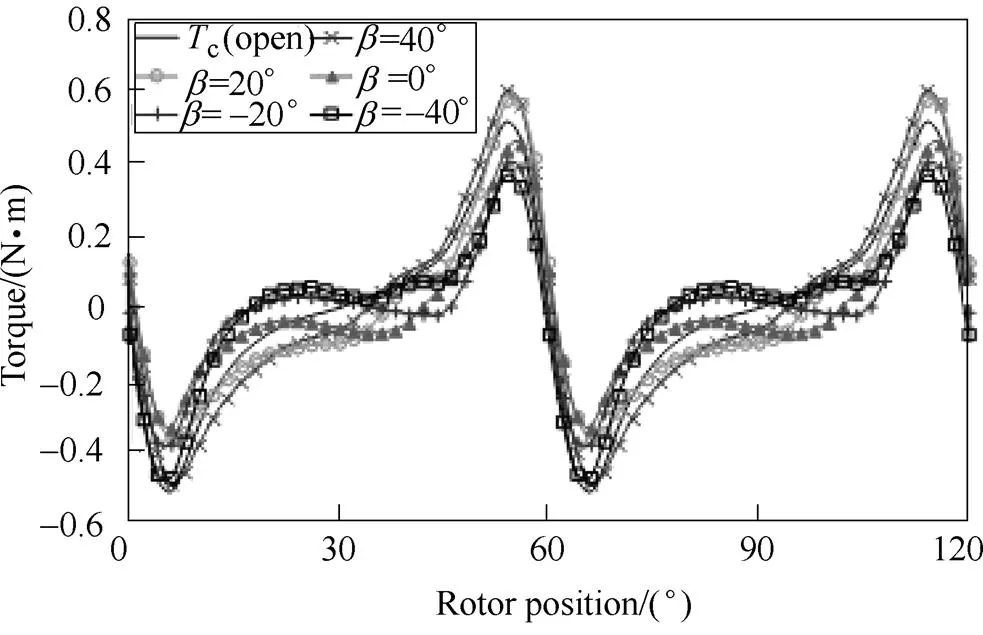
(b) By Equ.(17) based on magnetic energy derivation

Fig.10 Torque results of inset PM machine with on-load PM field only when Ia=4.0A[19]

6 On-load Torque Ripple Analyses

On-load torque ripple is undesirable since it could result in noise and vibration and is harmful to precise rotor position control. In PM machines, the on-load torque ripple is contributed by PM torque ripple, reluctance torque ripple and on-load cogging torque. However, the on-load torque ripple is often investigated as single resultant quantity. With the help of FP technique, it is possible to identify the contribution and variation of each on-load torque ripple component. This would greatly help the machine designs.

In Ref.[22], the on-load torque ripple of a 12s/10p IPM machine with rotor shaping is further investigated based upon the calculation of the on-load cogging torque, the on-load back EMF and the inductance variation. In Ref.[41], all on-load torque ripple components are calculated using FP technique. The design trade-off between the open-circuit cogging torque and the on-load torque ripple is then investigated in a 12s/8p SPM machine having different slot openings. In Ref.[49], an analytical model is developed to predict the on-load transient torque of IPM machines by including not only the fundamental but also the harmonics of flux linkages. The flux linkage harmonics are segregated by FP technique to further explain the torque ripple variation. By way of example, on-load torque components as well as the variation of torque ripple components with the slot opening in a 12s/8p SPM machine are presented in Fig.11[41].

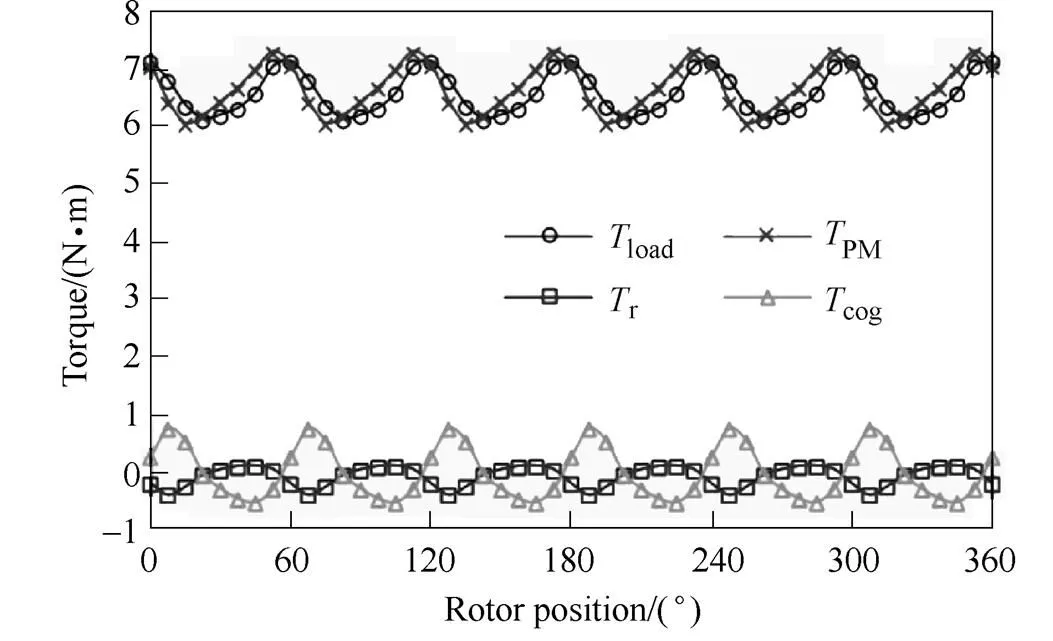
(a) On-load torque components when slot opening is 1mm

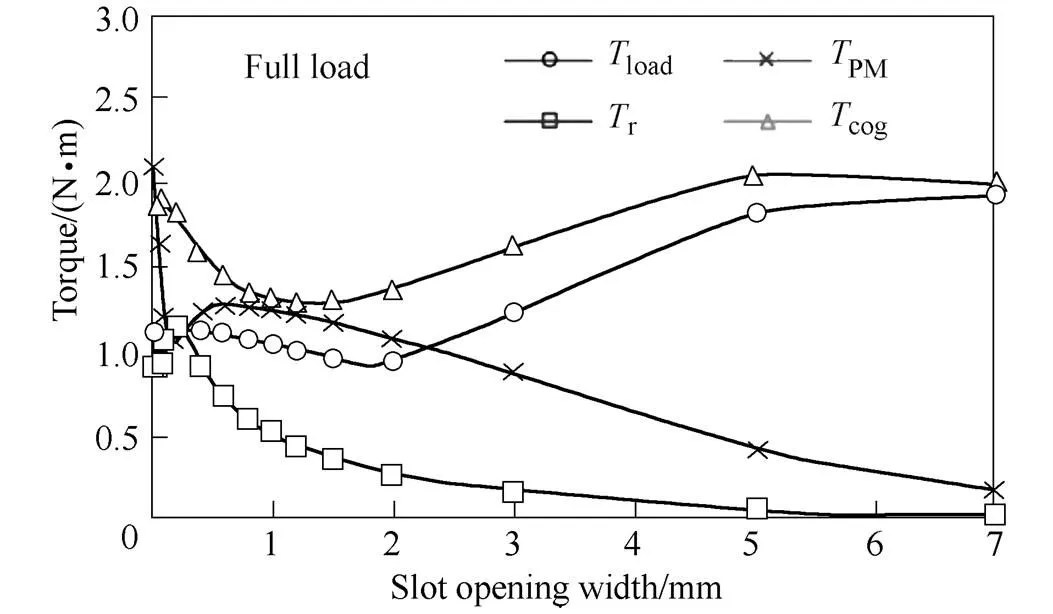
(b) Variation of torque ripple components with slot opening

Fig.11 On-load torque components and variations of torque ripple components with slot opening in a 12s/8p SPM machine when Ia=10A and =0°[41]

7 On-load Back EMF Analyses

Back EMF, which is produced by PM, is one of the most important quantities regarding the terminal voltage and output torque, both their average value and ripples. Normally, the back EMFs are investigated under the open-circuit condition. Due to the influence of magnetic saturation, the on-load back EMF can be significantly different from the open-circuit EMF. With the help of the FP technique, the on-load back EMF can be obtained based on the on-load PM flux linkage variation with the rotor position.

The relevant investigations on the on-load back EMFs can be found in Ref.[21,22] on a 12s/10p IPM machine with rotor shaping, Ref.[35] on a 12s/4p SPM machine, Ref.[50] on 24s/4p, 36s/6p, and 48s/8p multi-layer IPM machines as well as Ref.[51] on a 24s/4p SPM machine driven by a 6-step 3-phase BLDC inverter. All these investigations show that the on-load back EMFs are influenced by the electrical loading and can be significantly different from the open-circuit back EMFs. By way of example, the open-circuit and on-load back EMFs waveforms in Ref.[21] are presented in Fig.12.

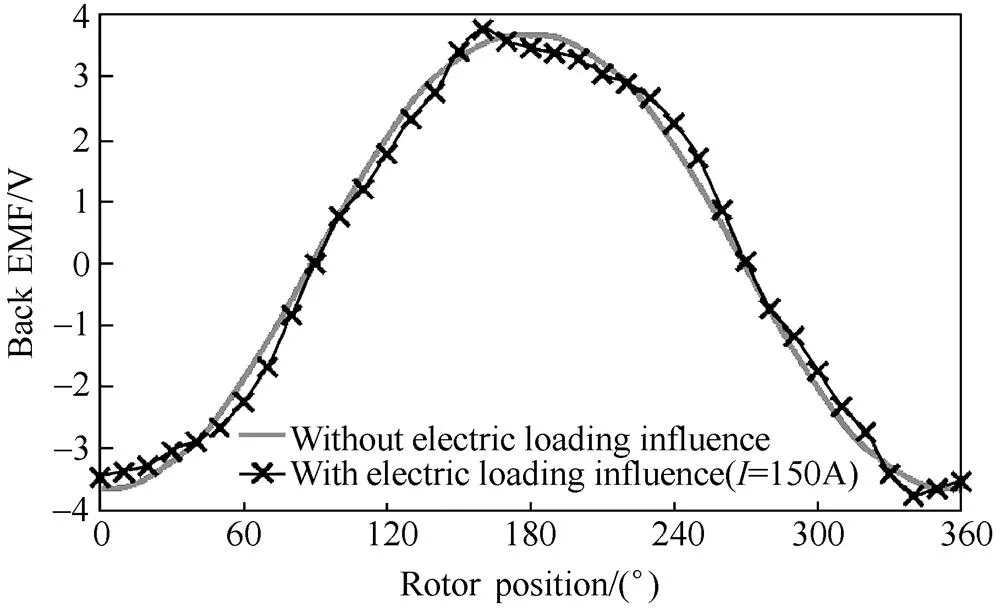
Fig.12 Open-circuit and on-load phase back EMF waveforms of 12s/10p IPM machine in Ref.[21]

8 On-load Voltage Waveform Analyses

When the load changes, not only the on-load back EMF but also the on-load voltage are affected. More importantly, the on-load voltage waveform may be greatly distorted from sinusoidal even when the open-circuit back EMFs are designed to be sinusoidal, as will be shown later. This on-load voltage distortion is harmful to various performance, especially the torque- speed curve. In order to investigate the mechanism of the on-load voltage distortion in various PM machines, the FP technique is employed in Ref.[52-57].

The investigation in Ref.[53] is focused on a 12s/8p SPM machine with its parameters and cross-section given in Tab.2 and Fig.13. The influence of slot/pole number combination in SPM machine is carried out in Ref.[54]. The investigation in Ref.[55] is focused on the fractional slot IPM machine while the influence of slot/pole number combination in IPM machine is carried out in Ref.[56,57] is focused on the comparison of torque-speed curves between 42s/8p and 48s/8p IPM machines considering the on-load voltage distortions.

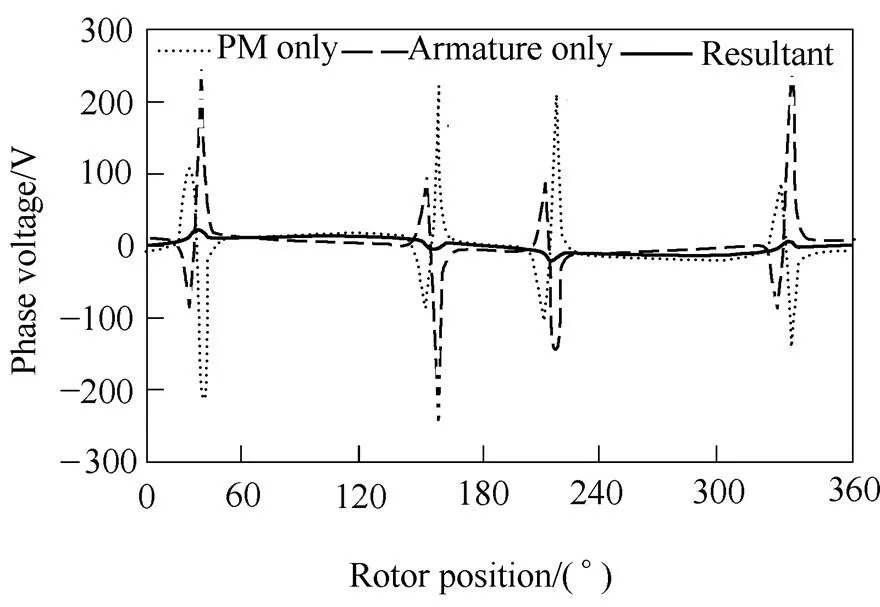
Fig.14 and Fig.15 show the waveforms of the voltage and flux linkage components of the 12s/8p SPM machine in Ref.[52] as an example. The machine parameters and cross-section are given in Tab.2 and Fig.13. It can be seen from Fig.13 that although the open-circuit back EMF is sinusoidal, the on-load voltage waveform is greatly distorted from sinusoidal and exhibits sharp voltage spikes. Based on the FP technique, it can be seen from Fig.14 that the sharp voltage spikes are results of sudden changes of both the PM and armature flux linkages. The sudden flux linkage changes are further due to the variation local magnetic saturation in the tooth-tips as shown in Fig.16.

Tab.2 Main parameters of 12s/8p SPM machine[52]

Fig.13 Cross-section of 12s/8p SPM machine in Ref.[52]

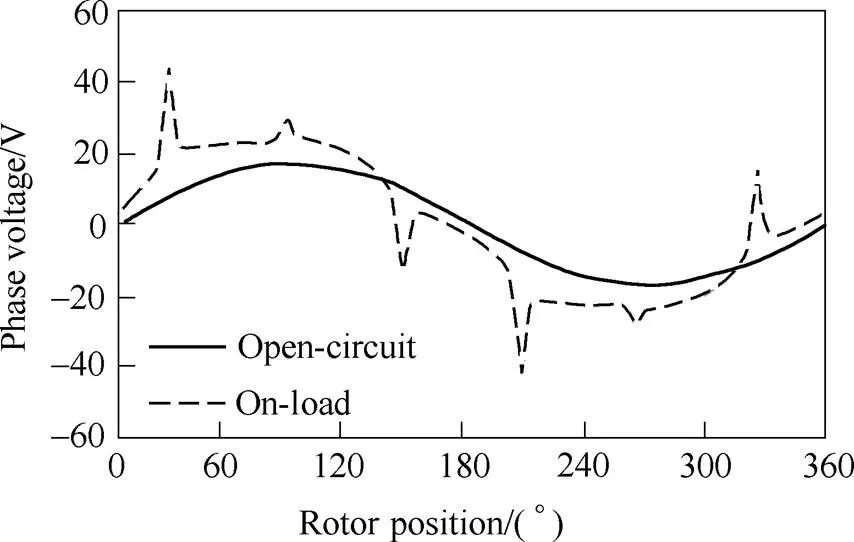
Fig.14 Open-circuit phase back EMF and on-load (Ia=10A and b =0°) terminal voltage waveforms of 12s/8p SPM machine[52]

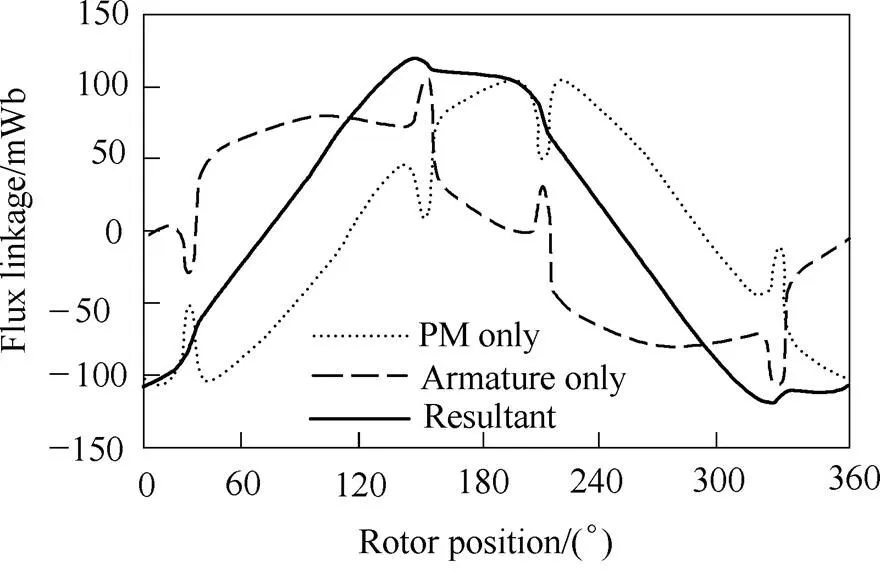
(a) Flux linkages

(b) Voltages

Fig.15 Flux linkage and voltage components of 12s/8p SPM machine when Ia=10A and =0°[52]

9 Flux Weakening Performance Analyses

Flux weakening control is an essential techniqueto achieve wide constant power speed range which is very often required for high performance electrical machines, such as electric vehicle applications. However, the constant parameter machine models could result in significant inaccuracy on the flux weakening performance prediction[15,58]. By using FP technique, the on-load flux linkages and inductances can be calculated. Then, it is possible to predict the flux weakening performance more accurately. The examples for flux weakening performance prediction based on FP technique calculated parameters can be found in Ref.[13,15,22,25,52-57,59]. However, it should be noted that the flux weakening performance prediction only based on the fundamental component of phase flux linkages (or average d- and q-axis flux linkages) could also result in large inaccuracy when the on-load voltage is distorted from sinusoidal[52-57]. It is due to that the voltage distortion will make the peak voltage much larger than the fundamental value. Consequently, the machine enters the flux weakening operation much earlier when the DC bus voltageDCis fixed.

(a) Locations of detecting points

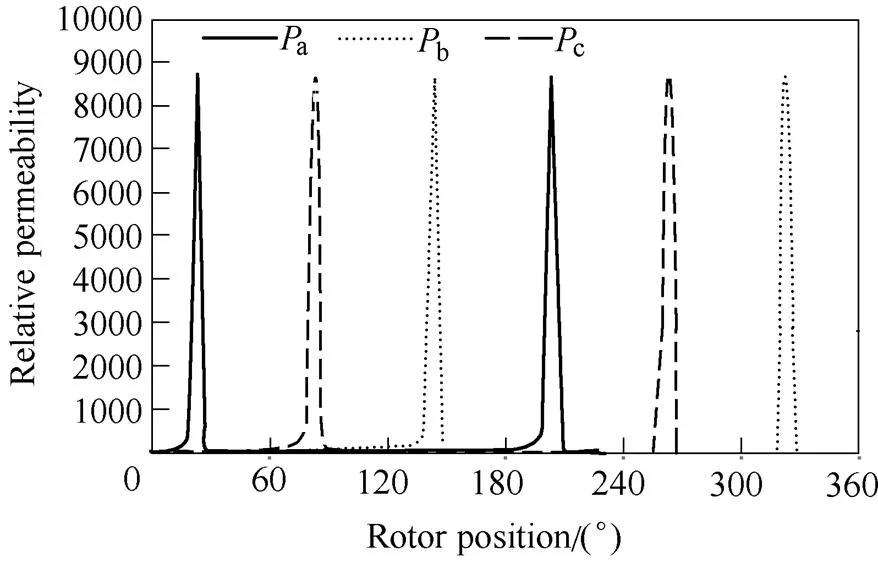
(b) Variation of permeability in tooth-tips

Fig.16 Relative permeability for tooth-tip bridges between each phase coils of 12s/8p SPM machine when Ia=10A and =0°[52]

The influence of on-load voltage distortion on the flux weakening performance of the 12s/8p SPM machine listed in Tab.2, which is presented in Ref.[52], is shown in Fig.17 as an example. It can be seen that the actual base speed considering the voltage distortion is much lower than the one considering the fundamental components only. The maximum torque in the deep flux weakening area also drops much faster when considering the voltage distortion.

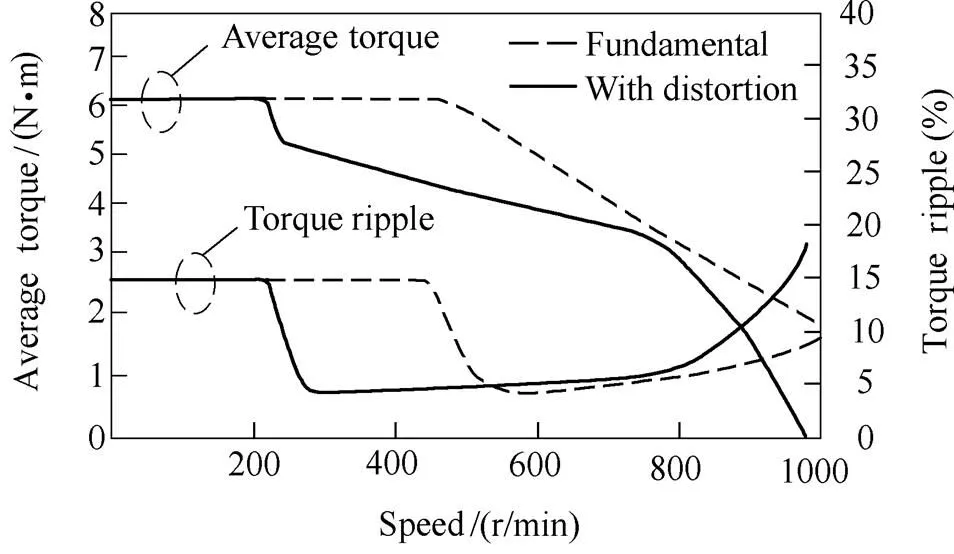
(a) Torque and torque ripple against speed

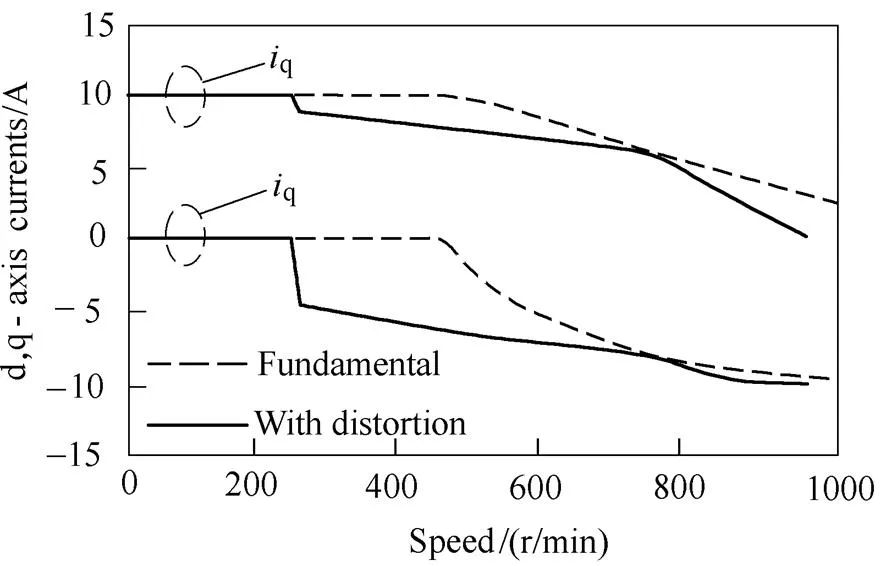
(b) d,q-axis currents against speed

Fig.17 Variation of torque-speed characteristics for different calculation methods of 12s/8p SPM machine when Ia=10A and UDC=42V[52]

10 Analyses on Other Issues

Except the aforementioned parameters and per- formance, the FP technique has also been used to help investigating other issues in PM machines. For example, in Ref.[60,61], the radial fore distributions are analyzed based on the on-load airgap flux density components. In Ref.[62], the on-load PM leakage flux through the iron bridge of an IPM machine with segmented PMs is obtained to explain the enhance- ment of its flux weakening capability.

11 Applications to Other Types of Electri- cal Machines

With the foregoing sections focused on the applications in PM machines, this section is dedicated to the applications of the FP technique to the other types of electrical machines.

The relevant applications to induction machines can be found in Ref.[63-65]. In Ref.[63], the FP technique is used to identify the influence of local magnetic saturation near the broken rotor bar on the stator current. In Ref.[64,65], the FP method is employed to calculate the equivalent circuit para- meters of induction machines, especially the leakage inductances.

For electrically excited machines, the relevant publications can be found in Ref.[66-68]. In Ref.[66], the on-load magnetic field and flux linkage com- ponents are obtained to explain the terminal voltage increase of a PM-assisted salient pole electrically excited machine. In Ref.[67,68], variation of inductances with the load is calculated to improve the maximum torque per ampere control of electrically excited machine under heavy magnetic saturation operations.

The investigations in Ref.[17] and Ref.[69] are on SR machines. In Ref.[17], the on-load phase flux linkage variations are obtained to explain the influ- ence of mutual coupling effect on torque production in SR machines having different winding topologies. In Ref.[69], the self- and mutual torques of conventional and mutually coupled SR machines are obtained based on the on-load self- and mutual flux linkages for performance comparison and selection of optimal current waveform.

In Ref.[43], the FP technique is used on a hybrid excited switched flux PM machine to obtain flux linkages and inductances for further performance investigation including torque components and torque- speed curves. In Ref.[70], the torque separation is conducted by FP technique to assist the optimization of a hybrid rare-earth-free PM reluctance machine.

12 Conclusion

The FP technique and its applications in various electrical machines have been comprehensively reviewed in this paper. It shows that the FP technique is able to accurately separate on-load magnetic field, flux linkage and inductance components in all types of electrical machines. The on-load field components and parameters can be further utilized for com- prehensive on-load performance analyses, such as average torque and torque ripple, voltage, flux weakening and radial force distribution. The accurate parameters can also improve the machine models and controls. All these features are very useful on developing high performance electrical machines.

Acknowledgments: The authors also thank Dr. Di Wu and Dr. Ziad Azar for their technical contributions.

Reference

[1] Chan C C. The state of the art of electric, hybrid, and fuel cell vehicles[J]. Proceedings of the IEEE, 2007, 95(4): 704-718.

[2] Zhu Z Q, Howe D. Electrical machines and drives for electric, hybrid, and fuel cell vehicles[J]. Proceedings of the IEEE, 2007, 95(4): 746-765.

[3] El-Refaie A M. Motors/generators for traction/ propulsion applications: a review[J]. IEEE Vehicular Technology Magazine, 2013, 8(1): 90-99.

[4] Cao W P, Mecrow B C, Atkinson G J, et al. Overview of electric motor technologies used for more electric aircraft (MEA)[J]. IEEE Transactions on Industry Electronics, 2012, 59(9): 3523-3531.

[5] Cheng M, Hua W, Zhang J, et al. Overview of stator- permanent magnet brushless machines[J]. IEEE Transactions on Industry Electronics, 2011, 58(11): 5087-5101.

[6] Zhu Z Q. Switched flux permanent magnet machines- innovation continues[C]//International Conference on Electrical Machines and Systems, 2011: 1-10.

[7] Eastham J F, Cox T, Proverbs J. Application of planar modular windings to linear induction motors by harmonic cancellation[J]. IET Electric Power App- lications, 2010, 4(3): 140-148.

[8] Levi E, Bojoi R, Profumo F, et al. Multiphase induction motor drives—a technology status review[J]. IET Electric Power Applications, 2007, 1(4): 489- 516.

[9] Bash M L, Pekarek S. Analysis and validation of a population-based design of a wound-rotor syn- chronous machine[J]. IEEE Transactions on Energy Conversion, 2012, 27(3): 603-614.

[10] Vijayakumar K, Karthikeyan R, Paramasivam S, et al. Switched reluctance motor modeling, design, simulation, and analysis: a comprehensive review[J]. IEEE Transactions on Magnetics, 2008, 44(12): 4605-4617.

[11] Bianchi N, Bolognani S, Bon D, et al. Torque harmonic compensation in a synchronous reluctance motor[J]. IEEE Transactions on Energy Conversion, 2008, 23(2): 466-473.

[12] Amara Y, Vido L, Gabsi M, et al. Hybrid excitation synchronous machines: energy-efficient solution for vehicles propulsion[J]. IEEE Transactions on Vehicular Technology, 2009, 58(5): 2137-2149.

[13] Bianchi N, Bolognani S. Magnetic models of saturated interior permanent magnet motors based on finite element analysis[C]//IEEE Industrial App- lication Conference, St. Louis, MO, USA, 1998: 27- 34.

[14] Williamson S, Knight A M. Performance of skewed single-phase line-start permanent magnet motors[J]. IEEE Transactions on Industry Applications, 1999, 35(3): 577-582.

[15] Kang G H, Hong J P, Kim G T, et al. Improved parameter modeling of interior permanent magnet synchronous motor based on finite element analysis[J]. IEEE Transactions on Magnetics, 2000, 36(4): 1867- 1870.

[16] Hu J, Zou J, Liang W. Finite element calculation of the saturation dq-axes inductance for a direct drive PM synchronous motor considering cross-magneti- zation[C]//International Conference on Power Elec- tronics and Drive Systems, 2003: 677-681.

[17] Walker J A, Dorrell D G, Cossar C. Effect of mutual coupling on torque production in switched reluctance motors[J]. Journal of Applied Physics, 2006, 99(10): 08R304(1-3).

[18] Walker J A, Dorrell D G, Cossar C. Flux-linkage calculation in permanent-magnet motors using the frozen permeabilities method[J]. IEEE Transactions on Magnetics, 2005, 41(10): 3946-3948.

[19] Chu W Q. Investigation of torque characteristics of permanent magnet and electrically excited machines[D]. UK: The University of Sheffield, 2013.

[20] Kwak S Y, Kim J K, Jung H K. Characteristic analysis of multilayer-buried magnet synchronous motor using fixed permeability method[J]. IEEE Transactions on Energy Conversion, 2005, 20(3): 549-555.

[21] Azar Z. Electromagnetic performance of fractional slot interior permanent magnet and synchronous reluctance brushless ac machines having non- overlapping concentrated windings[D]. UK: The University of Sheffield, 2012.

[22] Azar Z, Zhu Z Q, Ombach G. Influence of electric loading and magnetic saturation on cogging torque, back-EMF and torque ripple of PM machines[J]. IEEE Transactions on Magnetics, 2012, 48(10): 2650-2658.

[23] Alam F R, Abbaszadeh K. Magnetic field analysis in eccentric surface-mounted permanent-magnet motors using an improved conformal mapping method[J]. IEEE Transactions on Energy Conversion, 2016, 31(1): 333-344.

[24] Schmidt E, Susic M. Parameter evaluation of permanent magnet synchronous machines with tooth coil windings using the frozen permeabilities method with the finite element analyses[C]//IEEE Canadian Conference on Electrical & Computer Engineering, Montreal, QC, 2012: 1-5.

[25] Chen Q, Liu G, Zhao W, et al. Design and comparison of two fault-tolerant interior-permanent-magnet motors[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 6615-6623.

[26] Paula G T D, Monteiro J R B d A, Almeida T E P d, et al. Evaluation of surface mounted PM machine's parameters on load conditions using frozen permeabi- lity method. Part. I[C]//IEEE International Sym- posium on Industrial Electronics, Berlin, 2014: 806-811.

[27] Wang Q, Zhao B, Xu Y, et al. Inductances and phase coupling analysis of tubular permanent magnet machines with transverse flux configuration[C]// International Symposium on Electromagnetic Launch Technology, 2014: 1-5.

[28] Wang Q, Zhao B, Zhang J, et al. Inductances and phase coupling analysis of tubular permanent magnet machines with transverse flux configuration[J]. IEEE Transactions on Plasma Science, 2015, 43(5): 1232- 1235.

[29] Sun A, Li J, Qu R. Inductance calculation in variable-flux flux-intensifying permanent magnet synchronous machines using improved frozen per- meability method[C]//IEEE Magnetics Conference, Beijing, 2015: 1-1.

[30] Afinowi I, Zhu Z Q, Guan Y, et al. Electromagnetic performance of stator slot permanent magnet machines with/without stator tooth-tips and having single/double layer windings[J]. IEEE Transactions on Magnetics, 2016, 52(6): 8103410.

[31] Kim D, Hwang H, Bae S, et al. Analysis and design of a double-stator flux-switching permanent magnet machine using ferrite magnet in hybrid electric vehicles[J]. IEEE Transactions on Magnetics, 2016, 52(7): 8106604.

[32] Bianchi N, Alberti L. MMF harmonics effect on the embedded FE analytical computation of PM motors[J]. IEEE Transactions on Industry Applications, 2010, 46(2): 812-820.

[33] Chu W Q, Zhu Z Q. Average torque separation in permanent magnet synchronous machines using frozen permeability[J]. IEEE Transactions on Mag- netics, 2013, 49(3): 1202-1210.

[34] Ionel D M, Popescu M, McGilp M I, et al. Assessment of torque components in brushless permanent-magnet machines through numerical analysis of the elec- tromagnetic field[J]. IEEE Transactions on Industry Applications, 2005, 41(5): 1149-1158.

[35] Abbaszadeh K, Alam F R. On-load field component separation in surface-mounted permanent- magnet motors using an improved conformal mapping method[J]. IEEE Transactions on Magnetics, 2016, 52(2): 5200112(1-12).

[36] Paula G T D, Monteiro J R B d A, Almeida T E P d, et al. Evaluation of surface mounted PM machine's parameters on load conditions using frozen per- meability method. Part. II[C]//IEEE/IAS International Conference on Industry Applications, Berlin, 2014: 1-7.

[37] Zhao W, Zhao F, Lipo T A, et al. Optimal design of a novel V-type interior permanent magnet motor with assisted barriers for the improvement of torque characteristics[J]. IEEE Transactions on Magnetics, 2014, 50(11): 8104504(1-4).

[38] Zhao W, Chen D, Lipo T A, et al. Performance improvement of ferrite-assisted synchronous relu- ctance machines using asymmetrical rotor con- figurations[J]. IEEE Transactions on Magnetics, 2015, 51(11): 8108504(1-4).

[39] Zhao W, Lipo T A, Kwon B I. Optimal design of a novel asymmetrical rotor structure to obtain torque and efficiency improvement in surface inset PM motors[J]. IEEE Transactions on Magnetics, 2015, 51(3): 8100704(1-4).

[40] Fei W, Luk P C K, Miao D M, et al. Investigation of torque characteristics in a novel permanent magnet flux switching machine with an outer-rotor con- figuration[J]. IEEE Transactions on Magnetics, 2014, 50(4): 8100810(1-10).

[41] Wu D, Zhu Z Q. Design tradeoff between cogging torque and torque ripple in fractional slot surface- mounted permanent magnet machines[J]. IEEE Transa- ctions on Magnetics, 2015, 51(11): 8108704(1-4).

[42] Xu L, Liu G, Zhao W, et al. Analysis of new modular linear flux reversal permanent magnet motors[J]. IEEE Transactions on Magnetics, 2015, 51(11): 8109904(1-4).

[43] Li G J, Zhu Z Q, Jewell G. Performance investigation of hybrid excited switched flux permanent magnet machines using frozen permeability method[J]. IET Electric Power Applications, 2015, 9(9): 586-594.

[44] Tangudu J K, Jahns T M, El-Refaie A M, et al. Segregation of torque components in fractional-slot concentrated-winding interior PM machines using frozen permeability[C]//IEEE Energy Conversion Congress and Exposition, San Jose, CA, 2009: 3814- 3821.

[45] Xia B, Fei W, Luk P. Analysis and design of V-spoke ferrite interior permanent magnet machine for traction applications[C]//International Conference on Power Electronics Systems and Applications, Hong Kong, 2015: 1-6.

[46] Chen X, Wang J, Patel V I, et al. Reluctance torque evaluation for interior permanent magnet machines using frozen permeability[C]//IET International Conference on Power Electronics, Machines and Drives, Manchester, 2014: 1-6.

[47] Popescu M, Ionel D M, Miller T J E, et al. Improved finite element computations of torque in brushless permanent magnet motors[J]. IEE Proceedings on Electrical Power Applications, 2005, 152(2): 271-276.

[48] Chu W Q, Zhu Z Q. On-load cogging torque calculation in permanent magnet machines[J]. IEEE Transactions on Magnetics, 2013, 49(6): 2982-2989.

[49] Pina A J, Pramod P, Islam R, et al. Extended model of interior permanent magnet synchronous motors to include harmonics in d- and q-axes flux linkages[C]// IEEE Energy Conversion Congress and Exposition, Montreal, QC, 2015: 1864-1871.

[50] Seo J H, Kwak S Y, Jung S Y, et al. Investigation on EMF waveform in the interior permanent magnet synchronous machine considering load condition[C]// Biennial IEEE Conference on Electromagnetic Field Computation, Miami, FL, 2006: 321-321.

[51] Paula G T D, Monteiro J R B d A, Almeida T E P d, et al. Evaluation of surface mounted PM machine's parameters on load conditions using frozen per- meability method. Part. II[C]//International Con- ference on Electrical Machines, Berlin, 2014: 156- 161.

[52] Wu D. Effect of magnetic saturation in fractional slot PM machines with particular reference to terminal voltage distortion[D]. UK: The University of Sheffield, 2015.

[53] Wu D, Zhu Z Q. On-load voltage distortion in fractional slot surface-mounted permanent magnet machines considering local magnetic saturation[J]. IEEE Transactions on Magnetics, 2015, 51(8): 8106410(1-10).

[54] Wu D, Zhu Z Q. Influence of slot and pole number combinations on voltage distortion in surface- mounted permanent magnet machines with local magnetic saturation[J]. IEEE Transactions on Energy Conversion, 2015, 30(4): 1460-1471.

[55] Zhu Z Q, Wu D. On-load voltage distortion in fractional-slot interior permanent magnet machines[J]. IEEE Transactions on Magnetics, 2015, 51(10): 1-9.

[56] Zhu Z Q, Wu D, Ge X. Investigation of voltage distortion in fractional slot interior permanent magnet machines having different slot and pole number combinations[J]. IEEE Transactions on Energy Conversion, 2016, 31(3): 1192-1201.

[57] Zhu Z Q, Wu D, Wu M C, et al. Influence of on-load voltage distortion on torque-speed characteristic of interior permanent magnet machines[C]//IEEE Energy Conversion Congress and Exposition, 2015: 760- 767.

[58] Qi G, Chen J T, Zhu Z Q, et al. Influence of skew and cross-coupling on flux-weakening performance of permanent-magnet brushless AC machines[J]. IEEE Transactions on Magnetics, 2009, 45(5): 2110-2117.

[59] Chai S H, Lee B H, Hong J P, et al. Design of IPMSM having high power density for position sensorless operation with high-frequency signal injection and the method of calculating inductance profile[C]// International Conference on Electrical Machines and Systems, Beijing, 2011: 1-5.

[60] Dajaku G, Gerling D. Magnetic radial force density of the PM machine with 12-teeth/10-poles winding topology[C]//IEEE International Electric Machines and Drives Conference, Miami, FL, 2009: 1715-1720.

[61] Xia X P, Zhu Z Q, Wu L J, et al. Comparison of radial vibration forces in 10-pole/12-slot fractional slot surface-mounted and interior PM brushless AC machines[C]//International Conference on Electrical Machines, Rome, 2010: 1-6.

[62] Duan S, Zhou L, Wang J. Flux weakening mechanism of interior permanent magnet synchronous machines with segmented permanent magnets[J]. IEEE Transa- ctions on Apply Superconducting, 2014, 24(3): 1-5.

[63] Sprooten J, Gyselinck J, Maun J C. Local and global effect of a broken bar in induction machines using fundamental electromagnetic laws and finite element simulations[C]//IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives, Vienna , 2005: 1-6.

[64] Ling Z, Zhou L, Guo S, et al. Equivalent circuit parameters calculation of induction motor by finite element analysis[J]. IEEE Transactions on Magnetics, 2014, 50(2): 833-836.

[65] Jia L. Equivalent circuit parameters calculation of a wound rotor brushless doubly-fed machine based on finite element analysis[C]//IEEE Magnetics Con- ference, Beijing , 2015: 1.

[66] Shirai K, Tokikuni Y, Shima K, et al. Causes of increase in the terminal voltage of a permanent- magnet-assisted salient-pole synchronous machine[C]// International Conference on Electrical Machines and Systems, Tokyo, 2009: 1-6.

[67] Jeong I, Kim J, Kim Y, et al. Extended MTPA with cross coupling inductances for electrically excited synchronous motors[C]//IEEE Energy Conversion Congress and Exposition, Denver, CO, 2013: 867-873.

[68] Jeong I, Gu B G, Kim J, et al. Inductance estimation of electrically excited synchronous motor via polynomial approximations by least square method[J]. IEEE Transactions on Industry Applications, 2015, 51(2): 1526-1537.

[69] Li G J, Zhu Z Q, Ma X Y, et al. Comparative study of torque production in conventional and mutually coupled SRMs using frozen permeability[J]. IEEE Transactions on Magnetics, 2016, 52(6): 8103509.

[70] Hwang H, Bae S, Lee C. Analysis and design of a hybrid rare-earth-free permanent magnet reluctance machine by frozen permeability method[J]. IEEE Transa- ctions on Magnetics, 2016, 52(7): 8106304(1-4).

冻结磁导率先进技术及其在高性能电机研发中的应用

诸自强 褚文强

（谢菲尔德大学 谢菲尔德 S1 3JD 英国）

如何考虑磁场饱和的影响是当前电机设计中一个亟待解决的重要问题。近年来提出的冻结磁导率技术越来越多地被应用到电机负载电磁性能和参数计算中。本文详细阐述了冻结磁导率的原理及其在各种电机中的应用现状。研究表明，冻结磁导率技术可以用来精确分离各种电机负载状态下的电磁分量，如磁场、磁链、电感、转矩、转矩波动、反电势和端电压、弱磁性能以及径向力等均可以用冻结磁导率技术预测，并用来辅助电机及其驱动控制系统的设计。因此，冻结磁导率技术为高性能电机的研发提供了一个全新的方法。

电机 冻结磁导率 负载性能 永磁

TM301.4

June 20, 2016; Revised July 1, 2016.

Note brief

Professor Zhu Z Q, born in 1962, Fellow IEEE, Fellow IET, PhD, Professor at the University of Sheffield, UK. Major research interests include design, control, and applications of brushless permanent magnet machines and drives for applications ranging from automotive to renewable energy.

E-mail: Z.Q.Zhu@Sheffield.ac.uk (Corresponding author)

Dr Chu W Q, born in 1982, Principal Engineer, CSR Electric Drives Technology Research Centre, the University of Sheffield, UK. Major research interests include permanent magnet electrical machines and applications.

E-mail: chu.wenqiang@gmail.com

This work is partially supported by Guangdong Welling Motor Manufacturing Co. Ltd, Guangdong Innovative Research Team Program (2011N084), China, and the Royal Academy of Engineering/ Siemens Research Chair Program, UK.