磁致伸缩引起的非晶合金铁心振动解析计算及影响因素

吴胜男 唐任远 韩雪岩 佟文明 赵森磊



磁致伸缩引起的非晶合金铁心振动解析计算及影响因素

吴胜男 唐任远 韩雪岩 佟文明 赵森磊

（国家稀土永磁电机工程技术研究中心（沈阳工业大学） 沈阳 110870）

磁致伸缩是引起非晶合金电机振动噪声显著增大的主要原因之一。基于压磁方程建立了磁致伸缩引起的非晶合金圆环铁心振动解析模型。解析模型以振动位移为求解变量，采用分离变量法求解振动微分方程。解析模型可用于计算磁致伸缩引起的非晶合金铁心振动位移和振动加速度。通过测试不同加工工艺非晶合金铁心样品的振动，得出叠压和卷绕、浸漆和退火对非晶合金铁心振动的影响规律，确定不同加工工艺非晶合金铁心振动计算修正系数。本文研究工作为非晶合金电机振动噪声的研究奠定了基础。

磁致伸缩 非晶合金铁心 振动 解析计算 叠压和卷绕 浸漆和退火

0 引言

节能环保、发展绿色、低碳经济已受到人们的广泛重视。电机是应用量大、使用范围广的高耗能动力设备，推动电机节能具有重要的经济效益和社会效益。非晶合金材料作为一种新型软磁材料，具有优异的电磁性能（高磁导率、低损耗），将非晶合金材料应用于电机铁心能够显著降低电机的铁耗，提高电机效率和功率密度，节能效果显著[1]。尤其对于铁耗占主要部分的高端应用场合（如电动汽车发电机和驱动电机、高速主轴电机、航空电机、舰船电机、其他军事领域等），节能效果更好，具有广阔的应用前景。然而非晶合金材料具有磁致伸缩系数相对较大的缺点，由此引起的电机振动噪声显著增大[2]。

从20世纪70年代至今非晶合金电机的制造工艺、拓扑结构和优化设计技术在不断探索。美国通用电气公司（GE）早在1978年便申请了制造非晶合金定子铁心的专利[3]。GE的研究人员在1982年开发了一台额定功率250W的径向磁通非晶合金异步电机样机[4]。由于受非晶合金带材宽度的限制，电机定子铁心采用拼接工艺加工而成。虽然非晶合金定子铁心损耗降低了约80%，但是受加工工艺等因素的影响，电机效率仅提高了约1%。日立公司于2011年开发了一种定子铁心不开槽的400W、15 000r/min的小型高速轴向磁通永磁电机，定子铁心直接由非晶带材卷绕而成但不进行开槽[5]。美国莱特公司（LE）于2003年形成了一套适用于非晶合金轴向磁通电机定子铁心加工的工艺体系，后续进行了非晶合金电机整机工艺和技术开发。2007～2009年，LE公司开发的非晶合金轴向磁通永磁电机实现初步的产品化。目前非晶合金电机仍处于起步阶段，仅有少量应用。这一方面是由于非晶合金材料不易加工等因素造成的；另一方面则与非晶合金材料磁致伸缩系数大、叠压系数低，所开发样机在效率、振动噪声等方面的综合性能还不高有很大关系。

对于磁致伸缩引起的振动目前国内外大多数学者采用磁-机械耦合的方法进行数值计算。美国佛罗里达国际大学O. A. Mohammed等利用虚位移法对磁致伸缩力进行了计算[6,7]。根据物理学虚功原理，当磁通保持不变时，沿位移方向的电磁作用力等于磁能相对位移的变化。由于硅钢片被磁化时发生磁致伸缩引起内应力发生变化，磁导率随之变化，进而影响磁能的大小。这种方法通过考虑磁导率受应力影响计算磁致伸缩力。芬兰阿尔托大学K. Fonteyn等[8,9]同样采用虚位移法计算磁致伸缩力，并在此基础上建立磁-机械耦合模型。河北工业大学祝丽花等[10-12]、沈阳工业大学韩雪岩等[13]和比利时K. Delaere等[14,15]采用弹性力学方法对磁致伸缩力进行数值计算，并在此基础上建立了铁心磁-机械耦合模型。采用有限元法虽是用离散化模式代替原来的连续体，但在每个单元内部认为符合弹性力学基本假设。

目前国内外学者在研究磁致伸缩引起的振动时，普遍采用的求解方法为有限元法，对于磁致伸缩引起振动的解析计算方法还未见公开报道。此外，非晶合金铁心的加工制作工艺复杂，叠压和卷绕、浸漆和退火等加工将对非晶合金铁心的振动产生影响。本文从磁致伸缩引起振动的原理出发，基于压磁方程建立磁致伸缩引起的非晶合金铁心振动解析模型。实验测试了非晶合金磁致伸缩特性和不同加工工艺非晶合金铁心磁化特性。对不同频率下不同加工工艺非晶合金铁心振动进行了测试，总结叠压和卷绕、浸漆和退火加工对非晶合金铁心振动的影响规律，确定非晶合金铁心振动计算修正系数。

1 磁致伸缩引起的非晶合金铁心振动原理和解析模型

1.1 磁致伸缩引起非晶合金铁心振动原理

铁磁材料的磁致伸缩包含两个相互影响的效应，一个是磁致伸缩的焦耳效应，另一个是磁致伸缩的维拉里效应。所谓磁致伸缩的焦耳效应是指磁性材料在外磁场中由于磁化状态的改变，材料中的磁畴排列发生变化，导致材料尺寸在各个方向发生变化，如图1所示。同理，磁致伸缩的维拉里效应是指当材料由于拉伸或压缩发生形变，磁场也将发生变化，被称为逆磁致伸缩效应。非晶合金材料具有磁致伸缩特性，非晶合金铁心在交变磁场的作用下产生周期性的振动。

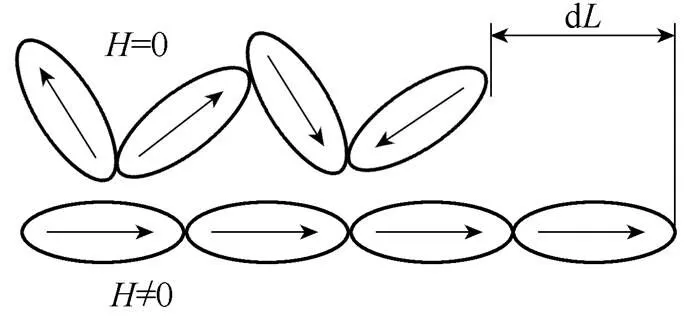
图1 铁磁材料在磁场作用下的磁致伸缩现象示意图

1.2 非晶合金圆环铁心振动解析模型

磁致伸缩特性是物体被磁化时的固有特性，非晶合金叠片铁心磁致伸缩引起的物体应变与磁场强度之间的关系可用压磁方程来描述，其张量形式表示为[16]

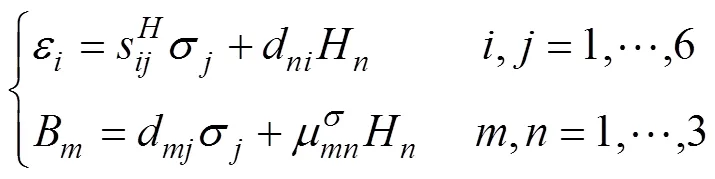
式中，为应变张量分量；s为常磁场下的弹性常数；为应力张量分量；为磁致伸缩系数；H为磁场强度矢量分量；B为磁通密度矢量分量；m为常压力下的磁导率。

非晶合金圆环铁心在圆周方向交变磁场作用下产生径向和轴向振动。为了分析方便，采用圆柱坐标系。磁场强度沿圆周方向分量为。

1）压磁方程

非晶合金圆环铁心的压磁方程为

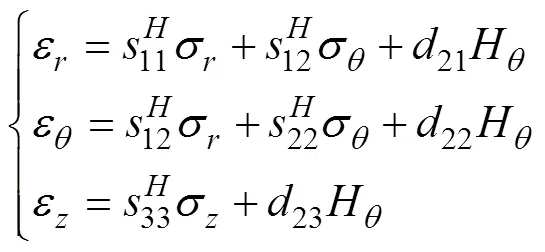
根据材料的物理性能，弹性常数11=22=33[17]，假设磁致伸缩为等体积变化[18]，压磁系数21=22，23=-22/2。由式（2）可得各应力分量、s、为

用杨氏模量和泊松比代替弹性常数、，则有，，代入式（3）得

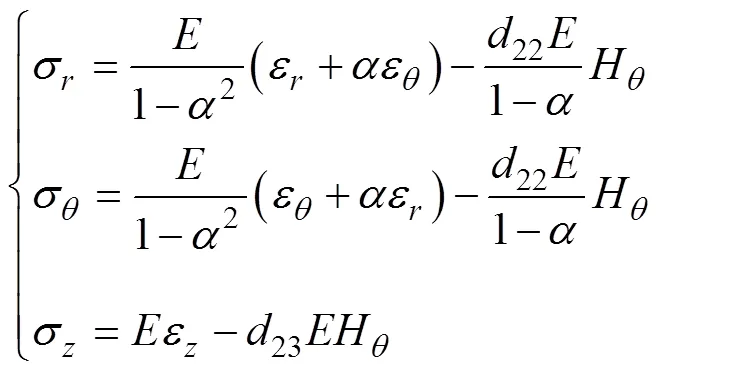
2）振动方程

非晶合金圆环铁心如图2a所示，设u为圆环铁心沿径向的振动位移，u为铁心沿轴向的振动位移。根据圆环振动理论[19]，铁心的各应变分量为

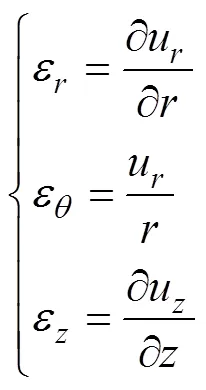
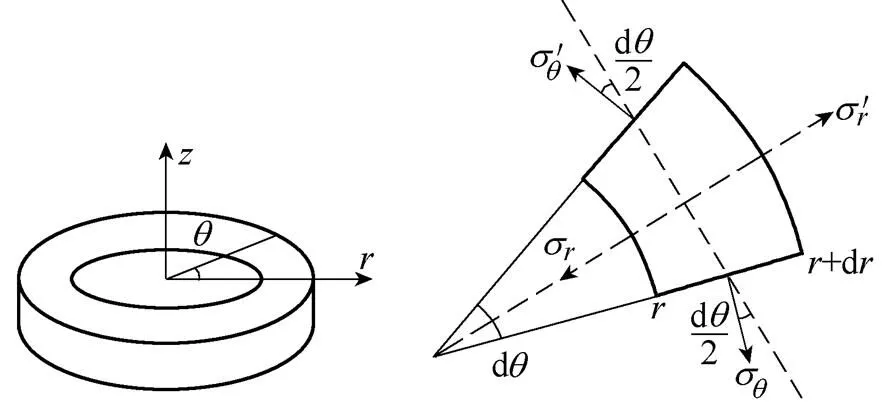
（a）铁心圆环体 （b）质量元

图2 铁心圆环和质量元示意图

Fig.2 The illustration of toroidal core and mass element

非晶合金圆环铁心的质量元小块如图2b所示，设非晶合金圆环铁心的密度为，则小块的质量为ddd。忽略振动阻尼，小块的振动微分方程为

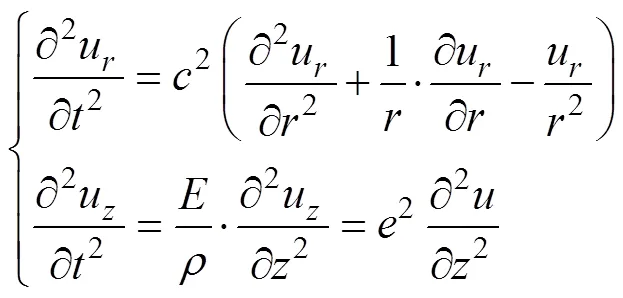
式中

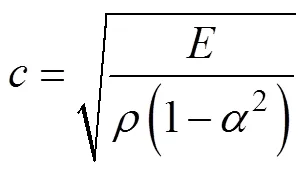
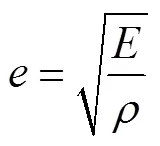
3）边界条件

非晶合金圆环铁心沿径向为机械自由，在边界上应力=0。圆环铁心沿轴向一端为固定约束边界条件，在边界上位移u=0。另一端为机械自由边界条件，在边界上应力=0。设1为铁心外半径，l为铁心轴向长度，其边界条件可表示为

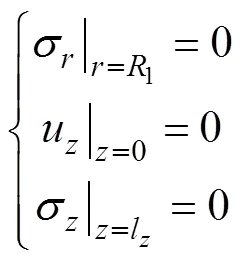
4）振动方程的通解

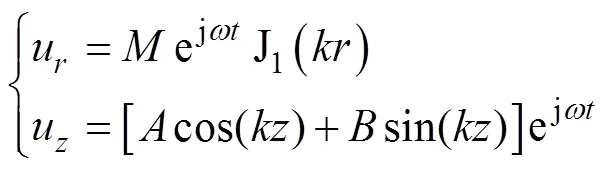
其中

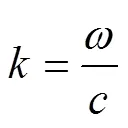
5）求解待定系数和满足边界条件的解

根据非晶合金圆环铁心边界条件，可得

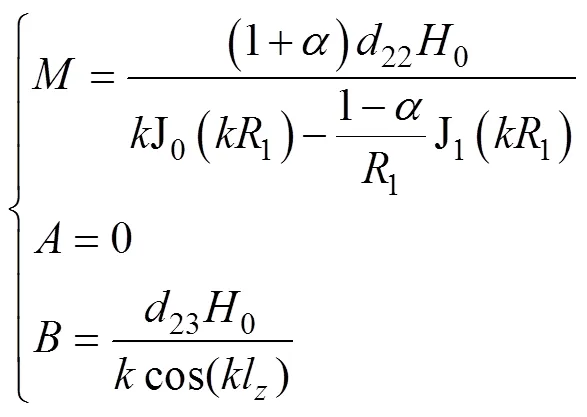
将常数、、代入式（11），即得到满足边界条件的解为

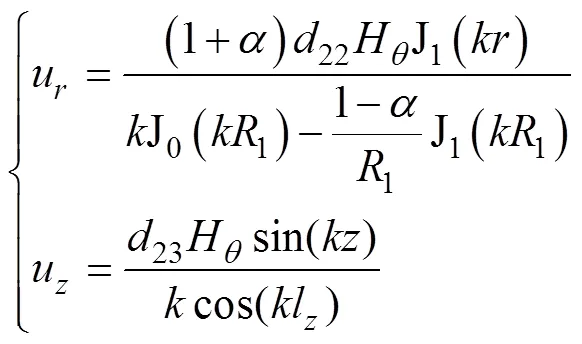
非晶合金圆环铁心的振动加速度为

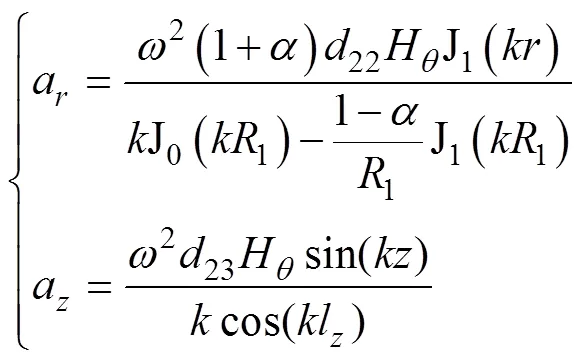
1.3 非晶合金磁致伸缩特性和磁化特性测试

非晶合金磁致伸缩特性和磁化特性是计算磁致伸缩引起铁心振动的基础。本文利用磁致伸缩测量系统（德国BROCKHAUS公司开发）对非晶合金磁致伸缩特性进行测试。测试样品为非晶合金2605SA1型号（Fe80B11Si9）带材，测试样品规格为长度600mm，宽度100mm。测试得到的非晶合金磁致伸缩特性曲线如图3所示，为磁致伸缩系数。

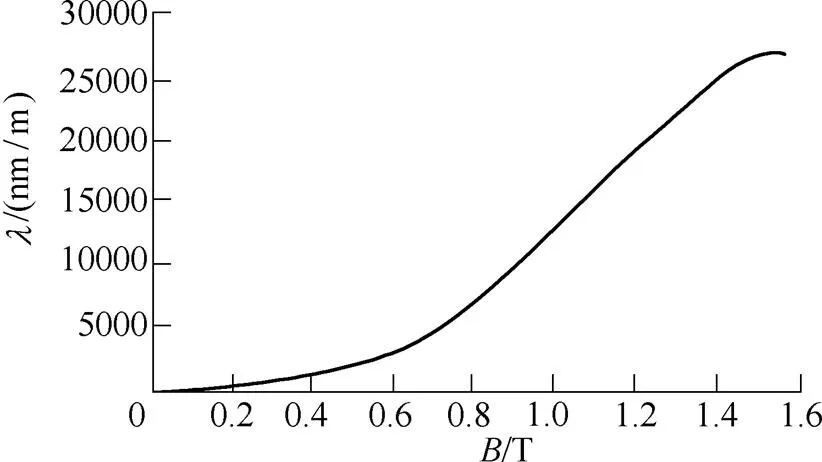
图3 非晶合金磁致伸缩特性曲线

按照国家标准GB/T 3658—2008《软磁材料交流磁性能环形试样的测量方法》，对叠压和卷绕、浸漆和退火不同加工工艺非晶合金铁心样品的磁化特性进行了测试，确定了叠压和卷绕、浸漆和退火不同加工工艺非晶合金铁心的磁化曲线和磁导率。非晶合金圆环铁心振动解析计算模型采用测试得到的磁致伸缩系数和磁导率。

1.4 非晶合金铁心振动影响因素

非晶合金铁心通常采用带材叠压和卷绕、退火和浸漆等工艺制作。一方面铁心各叠片层间存在的间隙和漆膜将引起铁心的力学性能（弹性模量等）改变；另一方面卷绕和叠压、浸漆和退火加工过程中铁心受到的应力和残余应力将引起铁心磁性能（磁致伸缩和磁化特性）发生改变。铁心加工过程中力学性能和磁性能的改变将影响铁心的振动特性。本文利用不同加工工艺铁心样品实验的方法研究叠压和卷绕、浸漆和退火加工对铁心振动的影响。引入非晶合金铁心振动计算修正系数，通过解析计算值和实验测试值的对比分析，确定不同加工工艺铁心振动计算修正系数。

2 非晶合金铁心振动测试方法

本文搭建实验平台对非晶合金铁心的振动进行测试。铁心振动实验采用自制测试线圈，在铁心绕上初级励磁线圈和次级感应线圈。初级励磁线圈连接交流电源，对初级励磁线圈施加激励，产生励磁磁动势。次级感应线圈连接电压表检测次级电压。非晶合金铁心振动测试电路如图4所示。

图4 铁心振动测试电路示意图

非晶合金铁心振动实验中无法直接测试铁心中的磁场强度和磁通密度，需要通过间接计算得到。通过励磁磁动势可以计算出铁心中的磁场强度

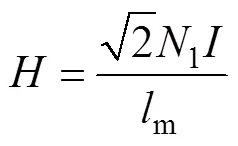
式中，为磁场强度（A/m）；1为初级励磁线圈的匝数；为初级励磁电流（A）；m为试样平均磁路长度（m）。

通过测试得到的次级电压可以计算出铁心中的磁通密度

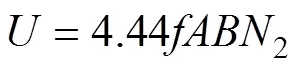
式中，为次级电压（V）；为频率（Hz）；为试样的横截面积（m2）；为磁通密度（T）；2为次级感应线圈的匝数。

在非晶合金铁心轴向和径向放置振动加速度计来检测铁心的振动，振动加速度传感器通过磁铁吸附在铁心表面，铁心振动加速度测试点如图5所示。非晶合金铁心振动实验采用丹麦B&K公司生产的振动测试装置进行测试，测试装置如图6所示。

（a）径向测试点 （b）轴向测试点

图5 振动加速度测试点

Fig.5 Measuring points of vibration acceleration

图6 振动测试装置

3 叠压和卷绕加工对非晶合金铁心振动的影响

非晶合金电机定子铁心通常采用非晶合金带材叠压和卷绕制成。叠压定子铁心加工是把非晶合金带材叠压成预定高度铁心，然后采用线切割进行开槽加工。卷绕定子铁心加工方式通常将非晶合金带材剪裁预定高度后卷绕成铁心，然后采用线切割进行开槽加工。叠压和卷绕加工过程中铁心受到的应力和残余应力不同，对铁心振动将产生不同的影响。

本文制作了非晶合金叠压和卷绕定子铁心各2个，铁心参数见表1，铁心样品如图7所示。叠压和卷绕定子铁心采用非晶合金2605SA1型号（Fe80B11Si9）带材制作，叠压铁心的叠压系数为0.94，卷绕铁心压紧系数为0.86，定子铁心开槽采用线切割加工工艺。

表1 叠压和卷绕非晶合金定子铁心参数

Tab.1 Amorphous metal core parameters

（a）叠压铁心 （b）卷绕铁心

图7 叠压和卷绕非晶合金测试铁心

Fig.7 Measuring cores with stacked and wound

上文建立了非晶合金圆环铁心振动解析模型，对于计算轴向或径向开槽铁心，主要考虑未开槽部分铁心（定子轭部），而开槽部分铁心（定子齿部）对振动的影响是通过一个附加质量来考虑的。这种推广参考了陈世坤主编的《电机设计》[20]。在采用解析模型计算时需要利用表1中的叠压和卷绕非晶合金定子铁心参数计算出定子轭部圆环体的有效尺寸和齿部尺寸。

3.1 非晶合金叠压铁心振动的计算与测试

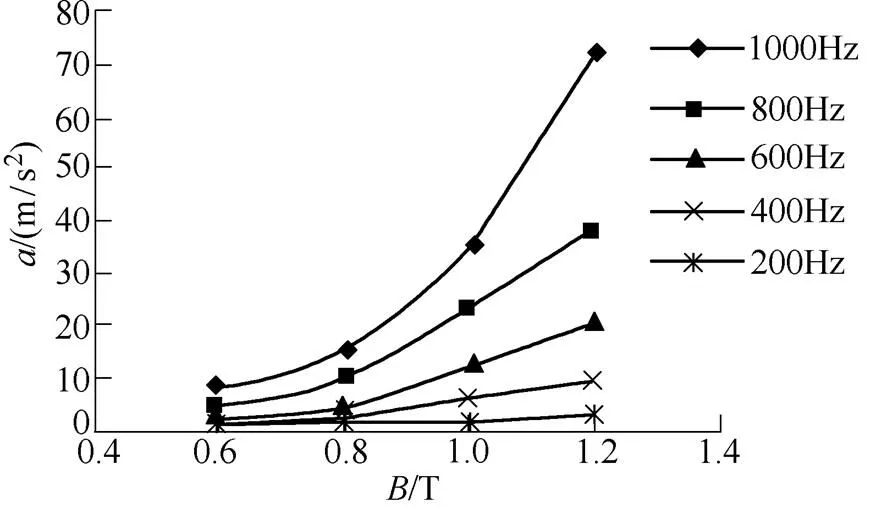
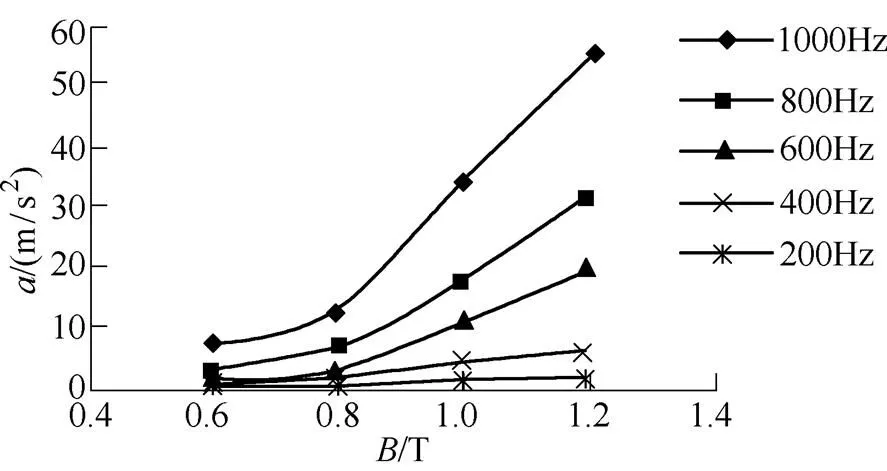
对不同供电频率下（=200Hz, 400Hz, 600Hz, 800Hz, 1 000Hz）非晶合金叠压定子铁心的振动进行了测试。分别选取叠压定子铁心径向和轴向测试点测试其振动加速度。不同频率下非晶合金叠压定子铁心径向和轴向振动加速度随磁通密度变化曲线如图8所示。从图8中可以看出，随着频率的增加，叠压定子铁心径向和轴向振动加速度增加；在频率一定时，随着磁通密度的增加，叠压定子铁心径向和轴向振动加速度增加。

表2和表3分别列出了磁通密度=1T时不同供电频率下非晶合金叠压定子铁心径向和轴向振动加速度计算和测试值。通过表中数据可以计算出不同频率下非晶合金叠压定子铁心径向和轴向振动加速度平均修正系数分别为1=1.12、2=1.38。

3.2 非晶合金卷绕铁心振动的计算与测试

对不同供电频率下（=200Hz, 400Hz, 600Hz,800Hz, 1 000Hz）非晶合金卷绕定子铁心的振动进行了测试。不同频率下非晶合金卷绕定子铁心径向和轴向振动加速度随磁通密度变化曲线如图9所示。从图9中可以看出，随着频率的增加，卷绕定子铁心径向和轴向振动加速度增加；在频率一定时，随着磁通密度的增加，卷绕定子铁心径向和轴向振动加速度增加。

（a）径向测试点

（b）轴向测试点

图8 不同频率下非晶合金叠压定子铁心振动加速度随磁通密度变化曲线

Fig.8 Vibration acceleration versus flux density in amorphous metal stacked stator cores under different frequencies

表2 非晶合金叠压铁心径向振动加速度计算和测试值

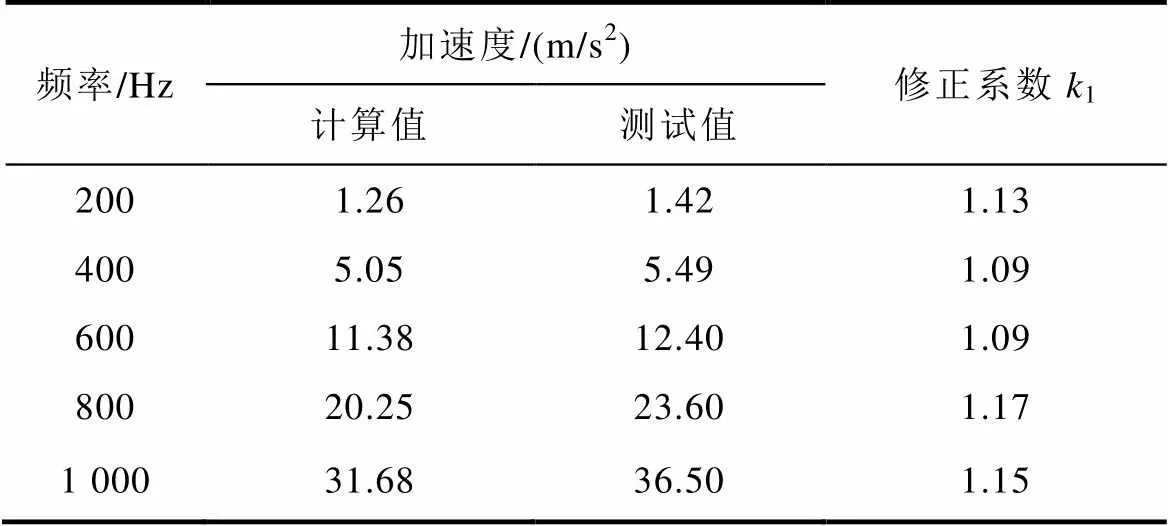
Tab.2 Results of analysis and measurement of vibration acceleration along radial direction

表3 非晶合金叠压铁心轴向振动加速度计算和测试值

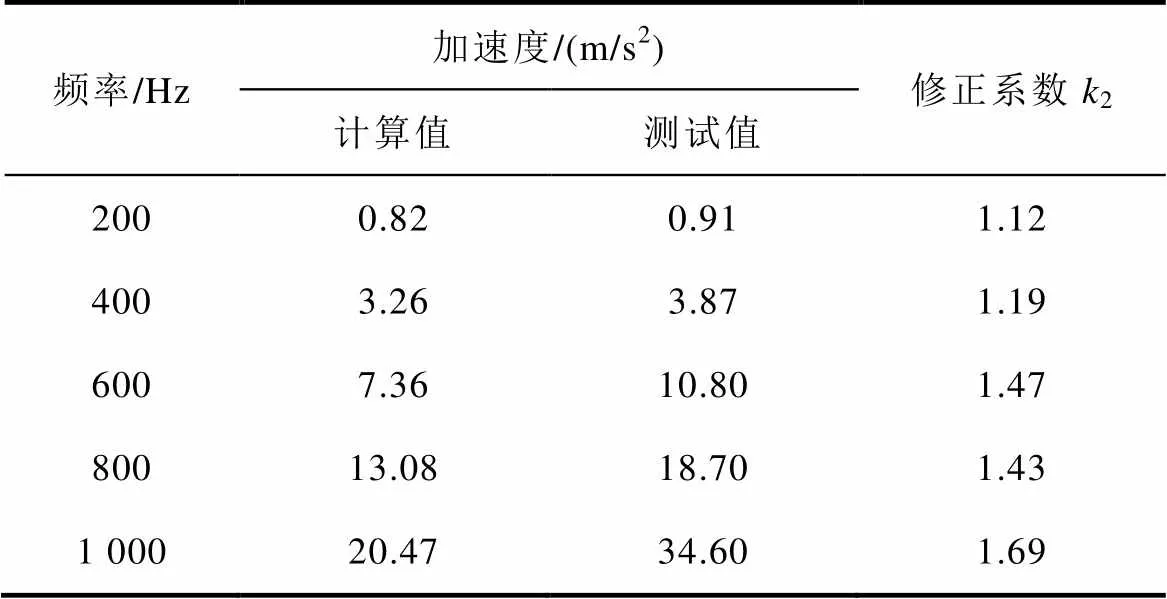
Tab.3 Results of analysis and measurement of vibration acceleration along axial direction

表4和表5分别列出了磁通密度=1T时不同供电频率下非晶合金卷绕定子铁心径向和轴向振动加速度计算和测试值。通过表中数据可以计算出不同频率下非晶合金卷绕定子铁心径向和轴向振动加速度平均修正系数分别为3=1.20、4=1.77。

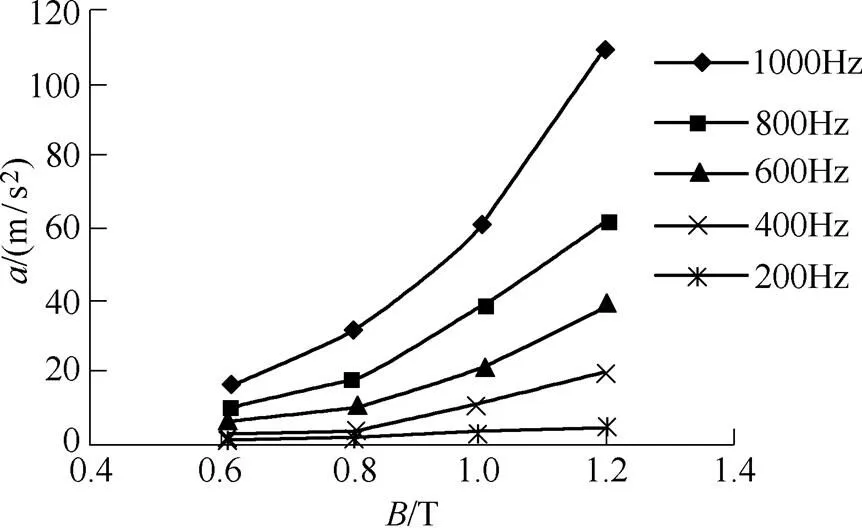
（a）径向测试点

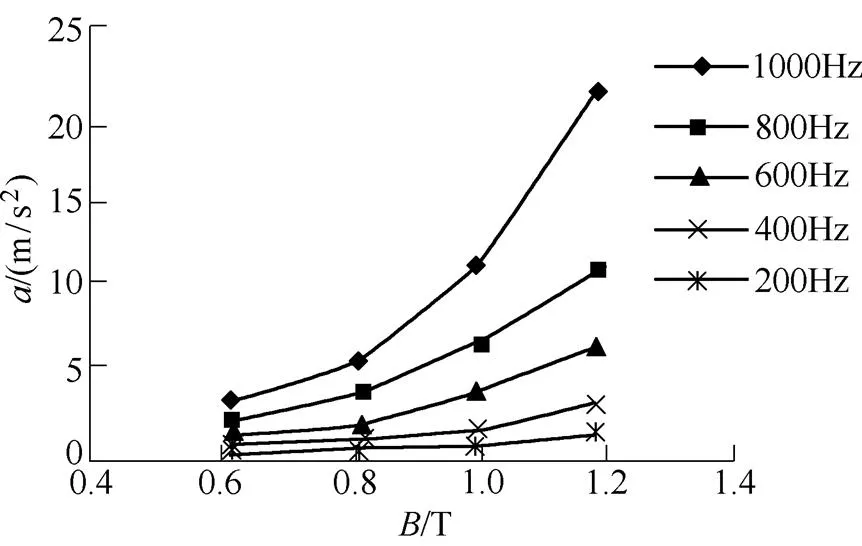
（b）轴向测试点

图9 不同频率下非晶合金卷绕定子铁心振动加速度随磁通密度变化曲线

Fig.9 Vibration acceleration versus flux density in amorphous metal wound stator cores under different frequencies

表4 非晶合金卷绕铁心径向振动加速度计算和测试值

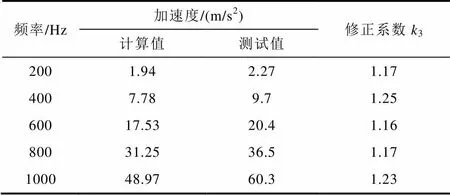
Tab.4 Results of analysis and measurement of vibration acceleration along radial direction

表5 非晶合金卷绕铁心轴向振动加速度计算和测试值

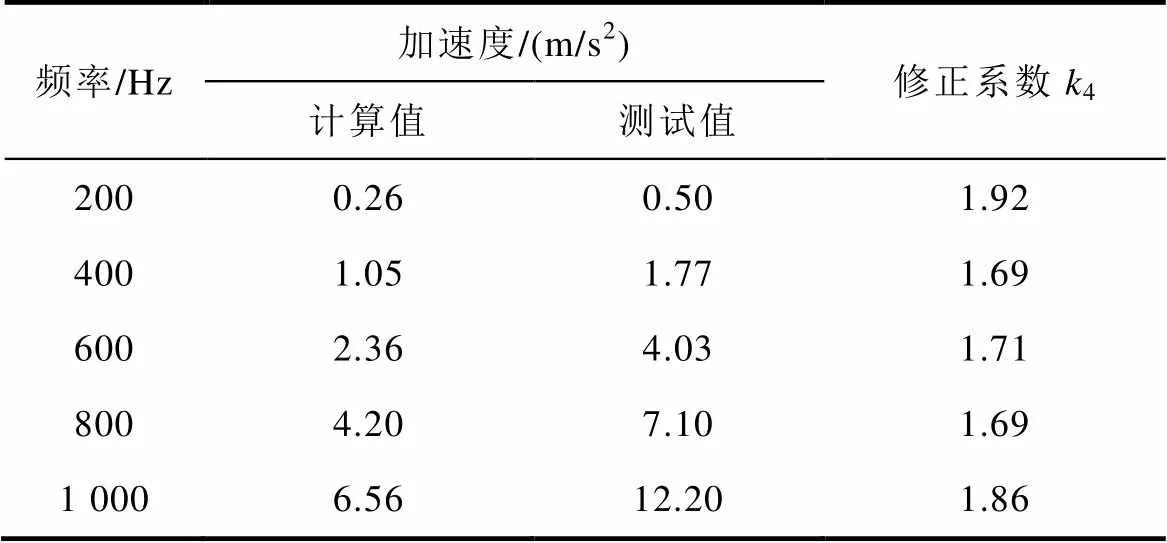
Tab.5 Results of analysis and measurement of vibration acceleration along axial direction

4 浸漆和退火加工对非晶合金卷绕铁心振动的影响

非晶合金铁心加工需要进行浸漆和退火处理。浸漆加工将在叠片铁心上产生残余应力，残余应力会对非晶合金铁心的力学性能和磁性能产生影响，进而对非晶合金铁心的振动产生影响。退火加工可以消除铁心内应力，也将对非晶合金铁心的振动产生影响。

本文制作采用卷绕工艺（剪裁预定高度后卷绕）、尺寸相同（外径60mm、内径40mm、高度20mm）、浸漆和退火不同加工方式非晶合金环形铁心样品。样品包括已退火未浸漆铁心、未退火已浸漆铁心各5个，测试铁心样品如图10所示。

图10 浸漆和退火不同加工工艺非晶合金测试铁心

4.1 已退火未浸漆卷绕铁心振动的计算与测试

对不同供电频率下（=200Hz, 400Hz, 600Hz, 800Hz, 1 000Hz）已退火未浸漆卷绕铁心的振动进行了测试。不同频率下已退火未浸漆卷绕铁心径向和轴向振动加速度随磁通密度变化曲线如图11所示。从图11中可以看出，随着频率的增加，已退火未浸漆卷绕铁心径向和轴向振动加速度增加；在频率一定时，随着磁通密度的增加，已退火未浸漆卷绕铁心径向和轴向振动加速度增加。

（a）径向测试点

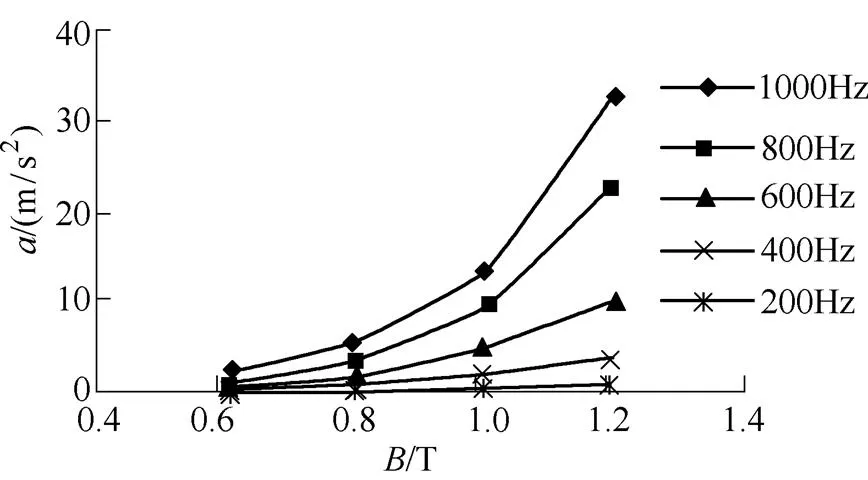
（b）轴向测试点

图11 不同供电频率下已退火未浸漆非晶合金卷绕铁心振动加速度随磁通密度变化曲线

Fig.11 Vibration acceleration versus flux density in annealed and undipped amorphous metal wound cores under different frequencies annealed

表6和表7分别列出了磁通密度=1T时不同供电频率下已退火未浸漆非晶合金卷绕铁心径向和轴向振动加速度计算和测试值。通过表中数据可以计算得出不同频率下已退火未浸漆非晶合金卷绕铁心径向和轴向振动加速度平均修正系数分别为5= 1.12、6=1.48。

表6 已退火未浸漆铁心径向振动加速度计算和测试值

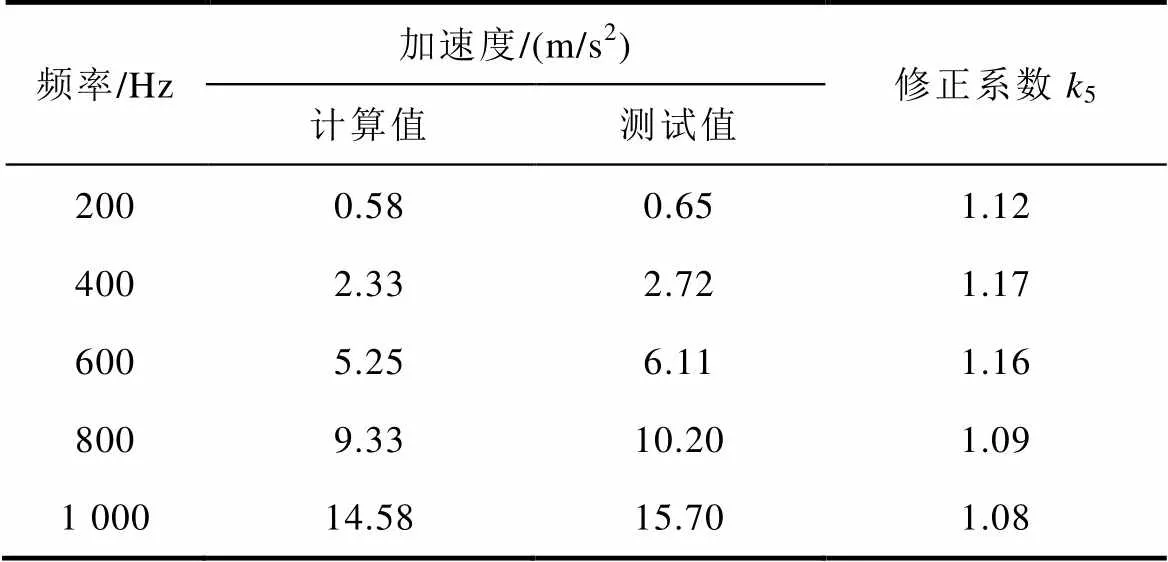
Tab.6 Results of analysis and measurement of vibration acceleration along radial direction

表7 已退火未浸漆铁心轴向振动加速度计算和测试值

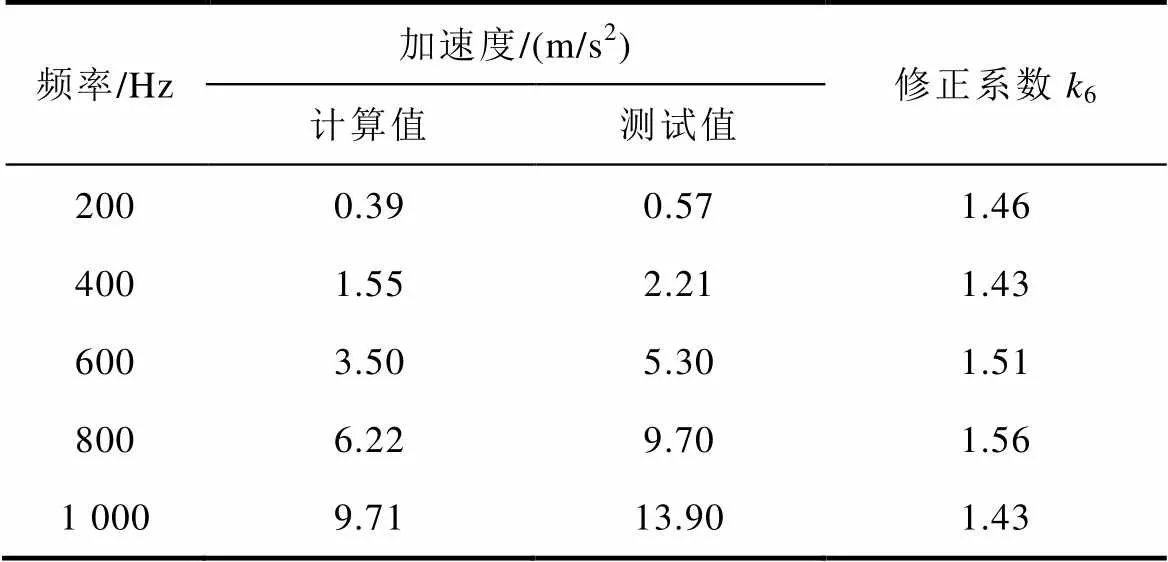
Tab.7 Results of analysis and measurement of vibration acceleration along axial direction

4.2 未退火已浸漆卷绕铁心振动的计算与测试

对不同供电频率下（=200Hz, 400Hz, 600Hz, 800Hz, 1 000Hz）未退火已浸漆非晶合金卷绕铁心的振动进行了测试。不同频率下未退火已浸漆卷绕铁心径向和轴向振动加速度随磁通密度变化曲线如图12所示。从图12中可以看出，随着频率的增加，未退火已浸漆卷绕铁心径向和轴向振动加速度增加；在频率一定时，随着磁通密度的增加，未退火已浸漆卷绕铁心径向和轴向振动加速度增加。

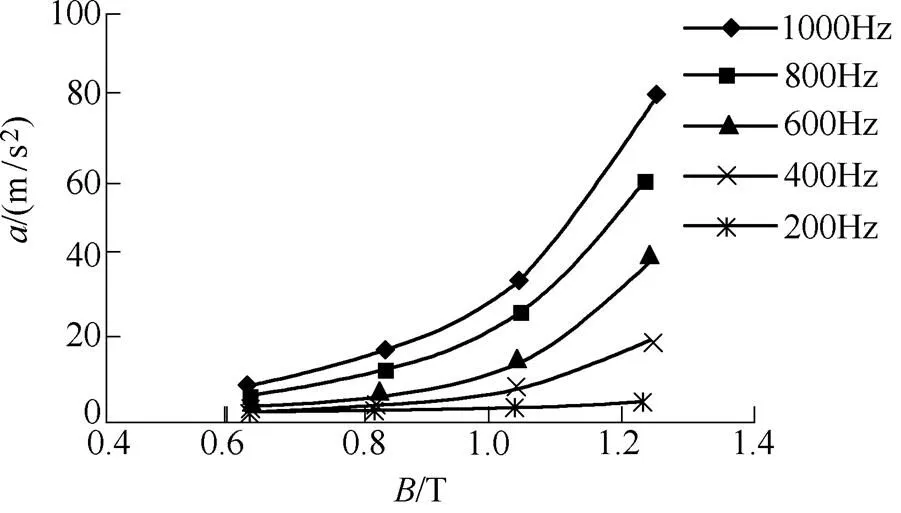
（a）径向测试点

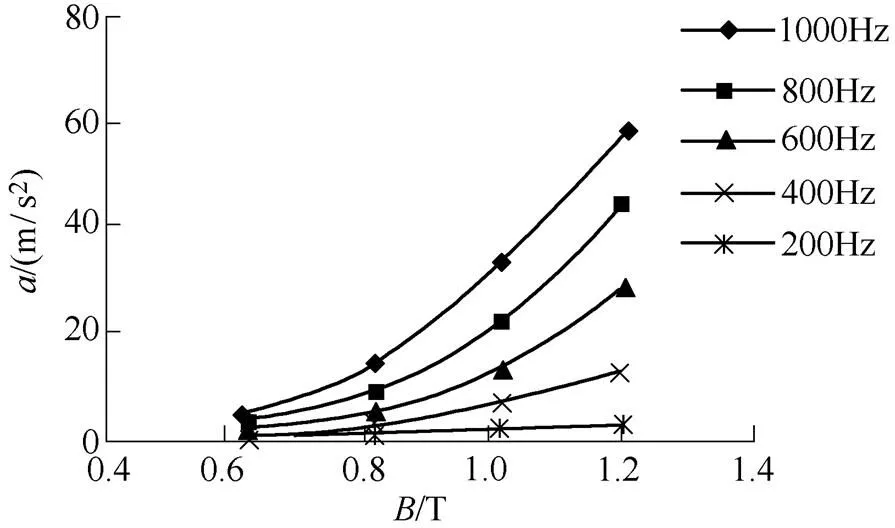
（b）轴向测试点

图12 不同频率下未退火已浸漆非晶合金卷绕铁心振动加速度随磁通密度变化曲线

Fig.12 Vibration acceleration versus flux density in unannealed and dipped amorphous metal wound cores under different frequencies

表8和表9分别列出了磁通密度=1T时不同供电频率下未退火已浸漆非晶合金卷绕铁心径向和轴向振动加速度计算和测试值。通过表中数据计算可以得出不同频率下未退火已浸漆非晶合金卷绕铁心径向和轴向振动加速度平均修正系数分别为7= 2.61、8=3.47。

表8 未退火已浸漆铁心径向振动加速度计算和测试值

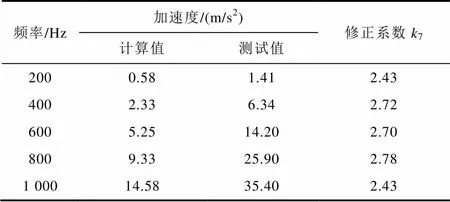
Tab.8 Results of analysis and measurement of vibration acceleration along radial direction

表9 未退火已浸漆铁心轴向振动加速度计算和测试值

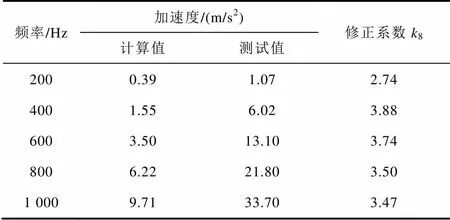
Tab.9 Results of analysis and measurement of vibration acceleration along axial direction

5 结论

本文基于压磁方程建立了磁致伸缩引起的非晶合金铁心振动解析模型。解析模型以振动位移为求解变量建立振动微分方程，采用分离变量法求解振动方程。解析模型可用于计算磁致伸缩引起的非晶合金铁心的振动位移、振动加速度。测试不同频率下叠压和卷绕、浸漆和退火不同加工工艺非晶合金铁心的振动，得出不同频率下叠压铁心径向和轴向振动加速度平均修正系数分别为1=1.12、2=1.38；卷绕铁心径向和轴向振动加速度平均修正系数分别为3=1.20、4=1.77；已退火未浸漆卷绕铁心径向和轴向振动加速度平均修正系数分别为5=1.12、6=1.48；未退火已浸漆卷绕铁心径向和轴向振动加速度平均修正系数分别为7=2.61、8=3.47。

附 录

非晶合金圆环铁心振动方程建立的具体过程如下。

忽略振动阻尼，小块的振动微分方程为

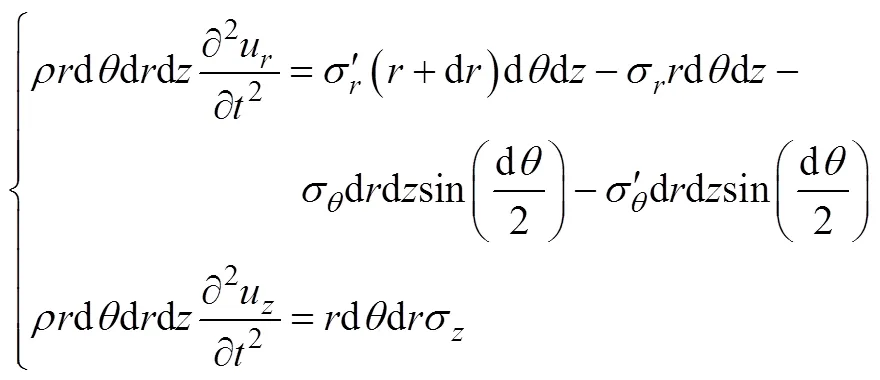
由于d和d都很小，故有

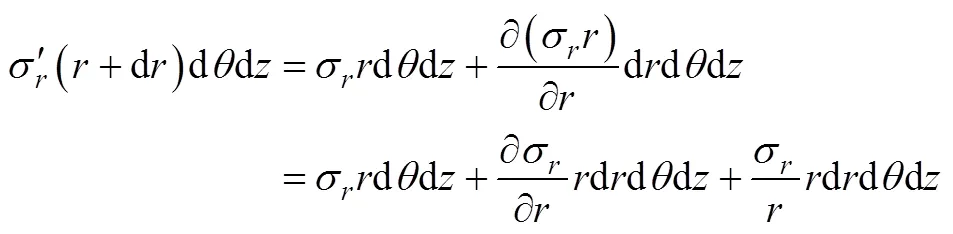
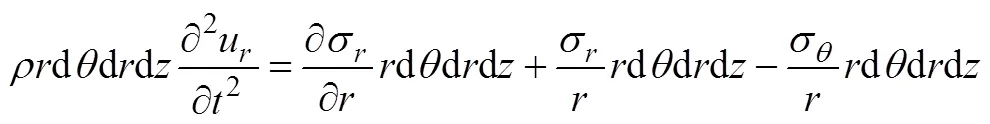
得到

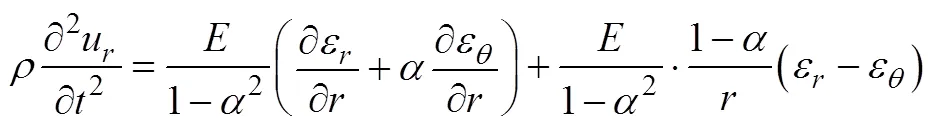
同时有

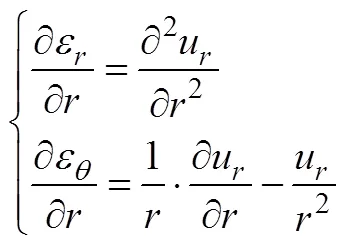
将式（A5）代入式（A4），得到非晶合金圆环铁心沿径向的振动方程为

化简式（A1）第2式，得到小块沿轴向的振动微分方程式

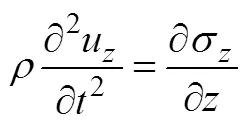
得到非晶合金圆环铁心沿轴向的振动方程为

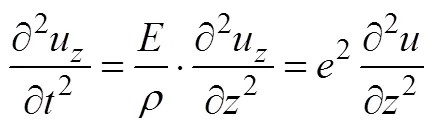
根据式（A6）和式（A8），得非晶合金圆环铁心振动微分方程式（6）。

参考文献：

[1] 佟文明, 朱晓锋, 朱龙飞, 等. 不同供电方式对非晶合金永磁同步电机铁耗的影响[J]. 电工技术学报, 2015, 30(10): 115-122.

Tong Wenming, Zhu Xiaofeng, Zhu Longfei, et al. The impact of different supply modes on core losses of amorphous alloy permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2015, 30(10): 115-122.

[2] 吴胜男, 唐任远, 韩雪岩, 等. 非晶合金卷绕定子铁心振动噪声的研究[J]. 电工技术学报, 2015, 30(11): 7-15.

Wu Shengnan, Tang Renyuan, Han Xueyan, et al. Research on vibration and noise of amorphous metal wound cores[J]. Transactions of China Electro- technical Society, 2015, 30(11): 7-15.

[3] Honsinger V B, Tompkins R E. Method and apparatus for fabricating amorphous metal laminations for motors and transformers: USA, US4155397[P]. 1978.

[4] Johnson L A, Cornell E P, Bailey D J, et al. Application of low loss amorphous metals in motors and transformers[J]. IEEE Transactions on Power Apparatus and Systems, 1982, 101(7): 2109-2114.

[5] Wang Z N, Enomoto Y, Masaki R, et al. Development of a high speed motor using amorphous metal cores[C]//8th International Conference on Power Electronics and ECCE Asia, Jeju, 2011: 1940-1945.

[6] Mohammed O A, Liu S, Abed N. Study of the inverse magnetostriction effect on machine deformation[J]. IEEE Transactions on Magnetics, 2004, 49(5): 1621- 1624.

[7] Mohammed O A, Liu S, Ganu S. Implementation of coupled magnetomechanical analysis including magnetostrictive effects in electric machinery[C]// International Latin American and Caribbean Con- ference for Engineering and Technology (LACCET), Miami Florida, 2004: 1-6.

[8] Fonteyn K, Belahcen A, Kouhia R. FEM for directly coupled magneto-mechanical phenomena in electrical machines[J]. IEEE Transactions on Magnetics, 2010, 46(8): 2923-2926.

[9] Fonteyn K, Belahcen A, Kouhia R. Contribution of maxwell stress in air on the deformations of induction machines[J]. Journal of Electrical Engineering & Technology, 2012, 7(3): 336-341.

[10] 祝丽花, 杨庆新, 闫荣格, 等. 考虑磁致伸缩效应电力变压器振动噪声的研究[J]. 电工技术学报, 2013, 28(4): 1-6.

Zhu Lihua, Yang Qingxin, Yan Rongge, et al. Research on vibration and noise of power transformer cores including magnetostriction effects[J]. Transa- ctions of China Electrotechnical Society, 2013, 28(4): 1-6.

[11] Zhu L H, Yang Q X, Yan R G, et al. Magnetoelastic numerical analysis of permanent magnet synchronous motor including magnetostriction effects and harmo- nics[J]. IEEE Transactions on Applied Supercon- ductivity, 2013, 46(1): 1-4.

[12] 祝丽花. 叠片铁心磁致伸缩效应对变压器、交流电机的振动噪声影响研究[D]. 天津: 河北工业大学, 2010.

[13] 韩雪岩, 赵森磊, 周挺, 等. 非晶合金电机振动噪声影响因素的研究[J]. 电工技术学报, 2015, 30(14): 531-538.

Han Xueyan, Zhao Senlei, Zhou Ting, et al. Research on vibration and noise of a amorphous metal motor[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 531-538.

[14] Delaere K, Heylen W, Hameyer K. Local mag- netostriction forces for finite element analysis[J]. IEEE Transactions on Magnetics, 2000, 36(5): 3115- 3118.

[15] Delaere K, Heylen W, Belmans R. Comparison of induction machine stator vibration spectra induced by reluctance forces and magnetostriction[J]. IEEE Transactions on Magnetics, 2002, 38(2): 969-972.

[16] Claeyssen F, Lhermet N, Letty R L, et al. Actuators, transducers and motors based on giant magneto- strictive materials[J]. Journal of Alloys Compounds, 1997, 258(1): 61-73.

[17] 王春雷, 李吉超, 赵明磊. 压电铁电物理[M]. 北京: 科学出版社, 2009.

[18] Delaere K, Heylen W, Belmans R. Comparison of induction machine stator vibration spectra induced by reluctance forces and magnetostriction[J]. IEEE Transactions on Magnetics, 2002, 38(2): 969-972.

[19] 李惠彬. 振动理论与工程应用[M]. 北京: 北京理工大学出版社, 2006.

[20] 陈世坤. 电机设计[M]. 北京: 机械工业出版社, 2004.

Analytical Calculation and Influence Factors of Vibration in Amorphous Metal Cores

（National Engineering Research Center for Rare Earth Permanent Magnet Machine Shenyang University of Technology Shenyang 110870 China）

An important source causing vibration and noise of machines with amorphous metal cores (AMCs) is magnetostriction effect of the magnetic material. In order to calculate the vibration due to magnetostriction, an analytical model for AMCs is set up based on piezomagnetic equations. Taking the vibration displacement as variable, the oscillatory differential equations are solved by the variable separation method. This analytical model can be used to predict vibration displacement and vibration acceleration of AMCs. Then the effect of producing processes including stacked and wound, dipped and annealed on vibration in AMCs was examined using measurements of vibration acceleration in AMCs, and related coefficients were also obtained. The outcomes lay a solid foundation for research on vibration and noise of machines with AMCs.

Magnetostriction, amorphous metal core, vibration, analytical calculation, stacked and wound, dipped and annealed

TM301

吴胜男 女，1985年生，博士研究生，研究方向为非晶合金永磁电机振动噪声。

E-mail: imwushengnan@163.com

唐任远 男，1931年生，教授，博士生导师，中国工程院院士，研究方向为永磁电机及其控制等。

E-mail: sgdtds@sina.com（通信作者）

2015-11-15 改稿日期 2016-05-14

国家重点研发计划（2016YFB0300500）和国家自然科学基金（51307111）资助项目。