基于FE-SEA混合法箱形梁结构噪声预测分析

罗文俊，杨鹏奇，张子正

(华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013)

轨道交通箱形梁产生的低频噪声会对人体的生理健康及精密仪器等有负面影响[1]。就目前而言，对该结构局部振动及噪声辐射的研究有待提高。桥梁结构噪声问题涉及领域广、研究对象多，研究对象间还存在相互作用关系，是一个复杂的综合体系。用解析方式研究复杂弹性体桥梁辐射的噪声场较难。近年来，国内外对桥梁结构噪声振动都进行了大量详细的研究。文献[2]考虑列车有关参数，结合特定的振动和波动方程，计算得到桥梁周围声场的声压辐射响应。文献[3]将实体单元作为基本研究对象，运用有限元方法对高速铁路高架箱形桥梁的局部振动进行详细分析。文献[4]将理论与试验结合，进一步分析预测列车运行状态下桥梁产生的振动响应规律，以及周围声场的声辐射响应变化情况。文献[5]采用车轨桥耦合振动理论，研究桥梁竖向振动及梁体面板声贡献量和声功率贡献。文献[6]结合有限元和声学软件对轨道交通桥梁振动噪声进行研究。文献[7]基于FE-SEA混合法，分析垂直轮轨力荷载下U形梁的局部振动与结构噪声特性。有限元法、边界元法、统计能量法是目前研究桥梁结构振动噪声的主要方法：在中、低频段范围内运用有限元法(FEM)计算较简单动力学系统精度较高，边界元法分析较高频时计算量较大且耗时，用有限元法和边界元法研究桥梁结构振动噪声一般只能分析200 Hz以下的较低频段，而统计能量法(SEA)在分析低频时预测精度大幅度下降。

本文运用FE-SEA混合法，在2.5～500 Hz范围内的不同频段分别建立箱形梁各板单元的FE、FE-SEA混合与SEA模型。在频域内对垂向轮轨力作用下箱形梁截面各板单元在2.5～500 Hz频率范围的局部振动及结构噪声特性进行分析，研究结构各板单元振动响应、声压贡献量、振动能量及箱形梁的振动功率损失，并与实测结果进行对比验证。

1 相关理论及预测模型

1.1 FE-SEA混合法基本原理及振动预测模型

FEM适用于低频，在单元足够多的情况下对低频的计算效率高；SEA适用于高频，在模态数足够多时，对高频的计算精度高。FE-SEA综合了FEM和SEA的优势，提高了FEM的高频计算效率同时也扩展了SEA的低频应用频率，可以进行全频段分析。可以将FE-SEA混合法[8]看做由若干子系统组合而成，应用时需确定组合系统中的FE子系统和SEA子系统。

在分析结构系统产生的振动声压辐射响应过程中，根据结构系统中各个子系统的带宽Δf及模态数n的关系，将分析的结构系统频段划分为不同的频段区：低频区、中频区和高频区。以模态密度1和5为界限，模态密度n不大于1为低频区；模态密度n不小于5为高频区；模态密度在1和5之间为中频区。

根据FEM和SEA的优势，分别在低频区建立FE模型、高频区建立SEA模型、中频区建立FE-SEA模型。FE子系统边界上的位移自由度定义为q，自由度q与作用在FE子系统边界上的外力f的关系方程式可以定义为

f=Dq

(1)

式中：D为动态刚度矩阵，其与频率有密切的联系。

frev=Ddirq-Dq

(2)

式中：Ddir为FE子系统动态刚度矩阵；frev为FE子系统的附加力。

将式(2)代入式(1)可得

frev+f=Ddirq

(3)

则节点之间的位移响应q满足

(4)

式中：Hdir为FE子系统动态刚度矩阵的共轭转置矩阵；E为研究分析结构系统中FE子系统和SEA子系统所产生的振动能量；G为格林函数；rjk为网格点j和k之间的距离；ω为角频率；n为FE子系统和SEA子系统的模态密度。

FE-SEA混合方程可以写成

(5)

(6)

(7)

(8)

由式(5)～式(8)，可以求得统计能量子系统的振动能量值。再由式(4)求得确定性子系统的位移响应后，进而可求得子系统的速度、加速度等物理量。在此基础上，由声辐射理论即可求得任意场点的传播声压。

以32 m高速铁路双线混凝土箱形梁为研究分析对象。梁体全长为32.6 m，宽度为11.4 m，梁高2.354 m；箱形梁左右腹板、左右翼板、顶板和底板厚度分别为0.28、0.28、0.35和3.946 m。采用FE-SEA混合法建立模型进行仿真计算，本文仿真计算分析频段为2.5～500 Hz，运用板单元提高了仿真分析模型仿真分析的精度与效率。根据各板单元的弯曲模态密度，以5为界限在不同的频段建立仿真分析计算模型。箱形梁各板单元的弯曲模态密度随频率变化的的规律如图1所示，结合宽频带激励完成分频段建模[9-10]。在2.5～160 Hz频段内建立FE模型，为提高仿真计算分析精度，FE子系统单元边长取0.2 m；在160～315 Hz频域内，箱形梁翼板单元建立FE子系统模型，腹板、顶板和底板建立SEA子系统模型；在315～500 Hz频段内，箱形梁各板单元模态密度均大于5，因此建为SEA子系统模型。在不同频段建立的仿真计算分析模型如图2所示。箱形梁各板单元在不同频段内的子系统分类见表1。

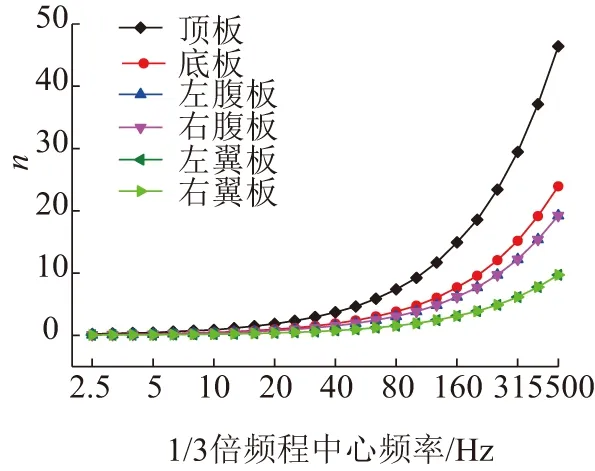
图1 箱形梁各板单元弯曲模态密度随频率的变化关系

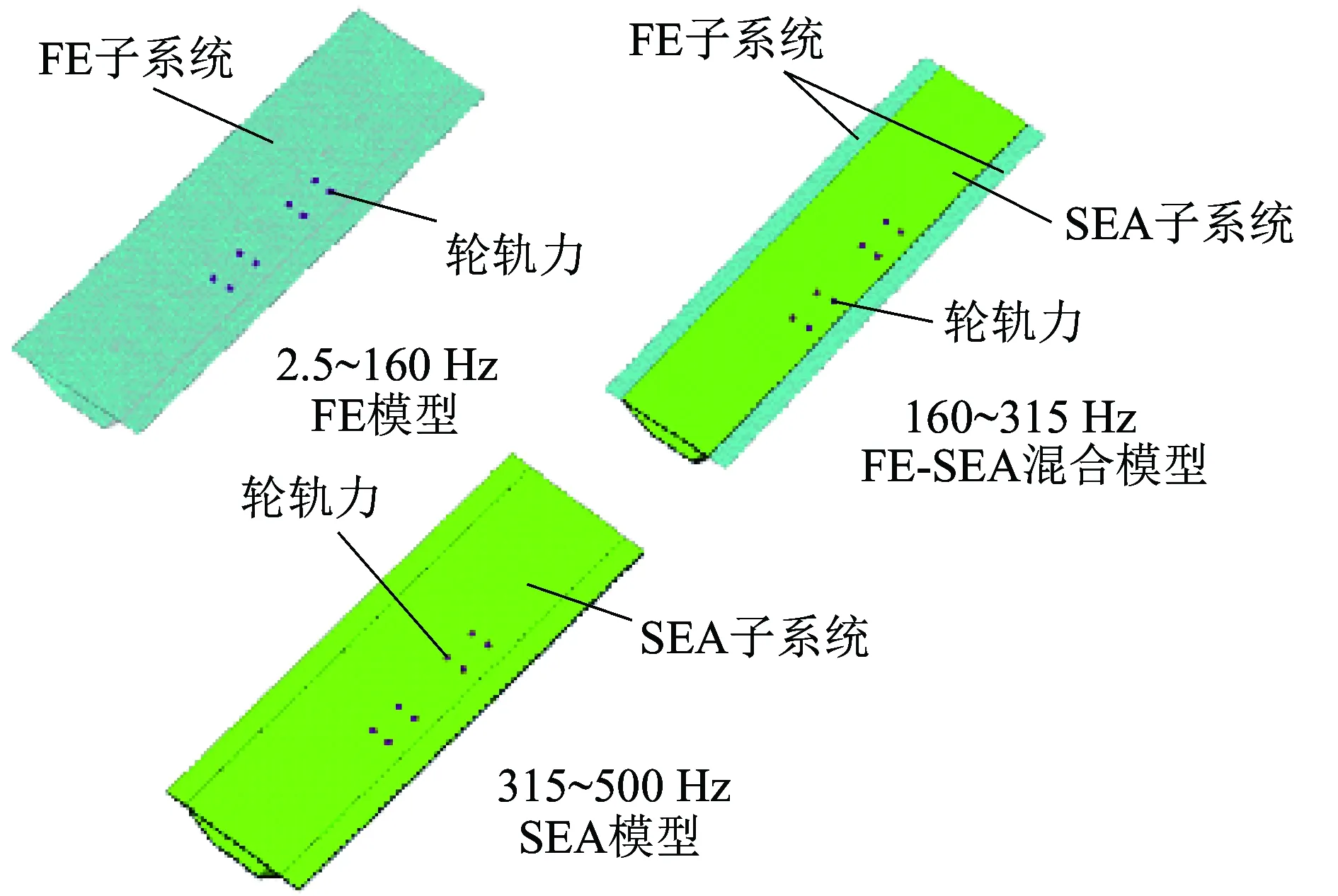
图2 箱形梁FE-SEA模型

表1 箱形梁板单元子系统分类

1.2 桥梁结构声辐射

箱形梁各个板单元结构可分别视为具有不同宽度(a)和长度(b)的矩形梁板结构子系统。各子系统辐射声功率为[4]

(9)

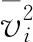
1.3 仿真分析流程

本研究的仿真计算分析技术如图3所示，通过SIMPACK建立车轨耦合模型，所建模型如图4所示，通过计算得到时域垂向轮轨力。在2.5～500 Hz范围内，分别在不同的频段建立FE、FE-SEA和SEA桥梁模型：在板单元模态密度数都小于5的频段内建立FE模型，板单元模态密度数都大于5的频段内建立SEA模型，在其余频段建立FE-SEA模型。根据箱形梁长度、轮距与车距，将频域内的轮轨力以最不利的形式施加于箱形梁中部位置，并在此基础上分析箱形梁的振动能量、预测箱形梁的振动及声压辐射响应的一般规律。

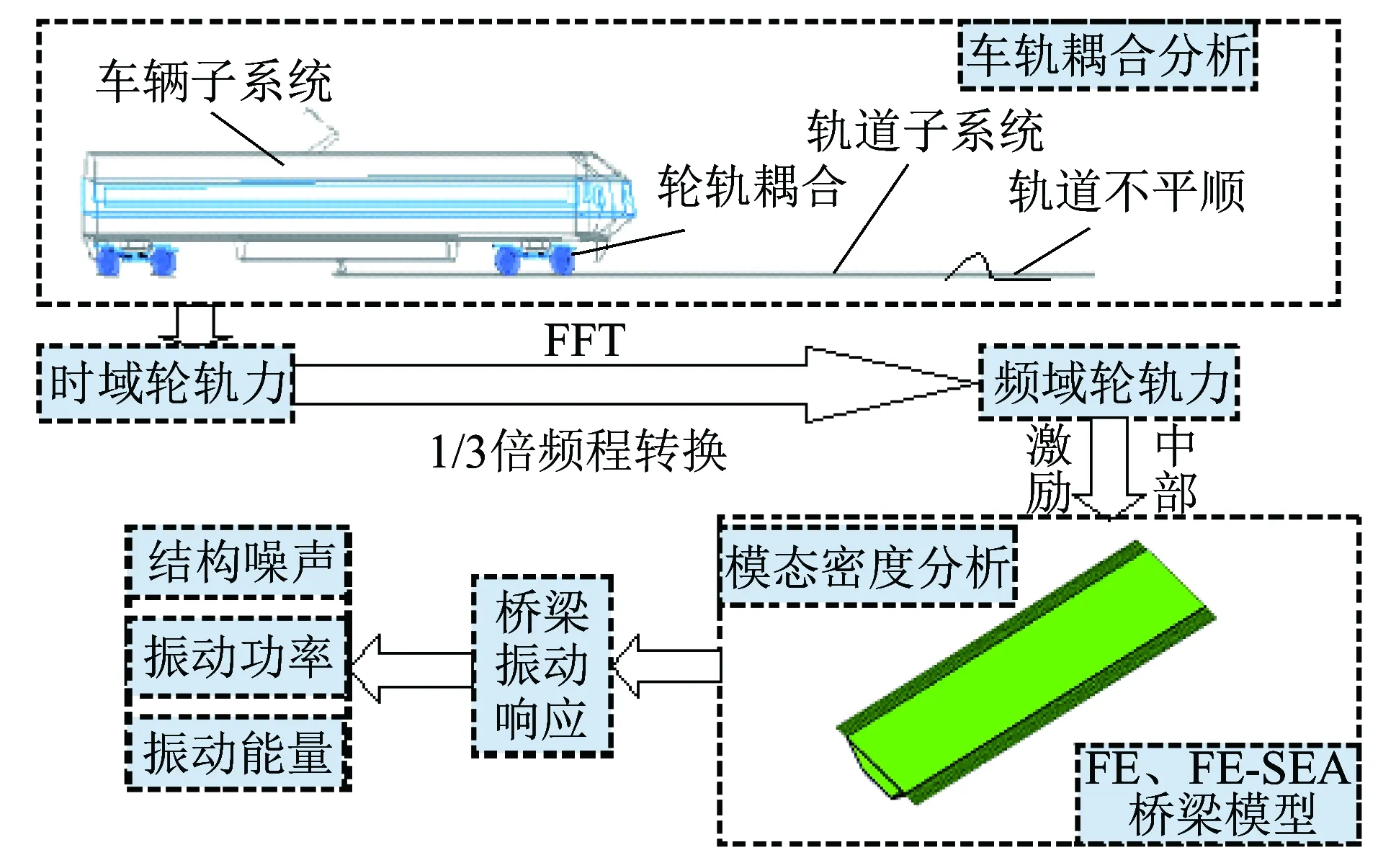
图3 仿真计算分析技术流程

图4 列车-无砟轨道-桥梁耦合系统(单位：m)

2 模型及相关参数

2.1 车轨耦合模型

选用CRH2动车组，车辆具体参数见表2。选用德国高干扰高低不平顺谱，钢轨选择UIC60型，轮轨为单点刚性接触，车速为140 km/h。在列车车轮与轨道模型中引入列车车轮和轨道的有关参数以及轮轨之间接触等相关因素，用来详细阐述轨道与列车车辆各个刚体之间的运动及受力关系。通过计算时域轮轨力，运用傅里叶变换将其转化为频域内轮轨力有效值，如图5(a)所示，再转换为1/3倍频程轮轨力，转换结果如图5(b)所示，轮轨力最大幅值所在频率均为50 Hz。

表2 CRH2动车组部分参数

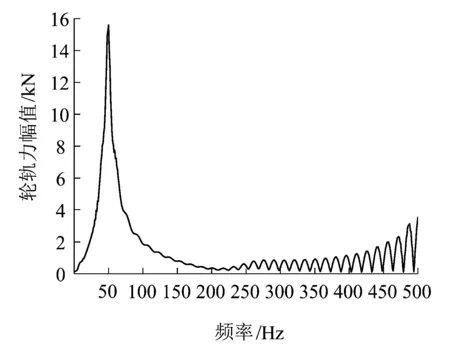
(a)轮轨力有效值

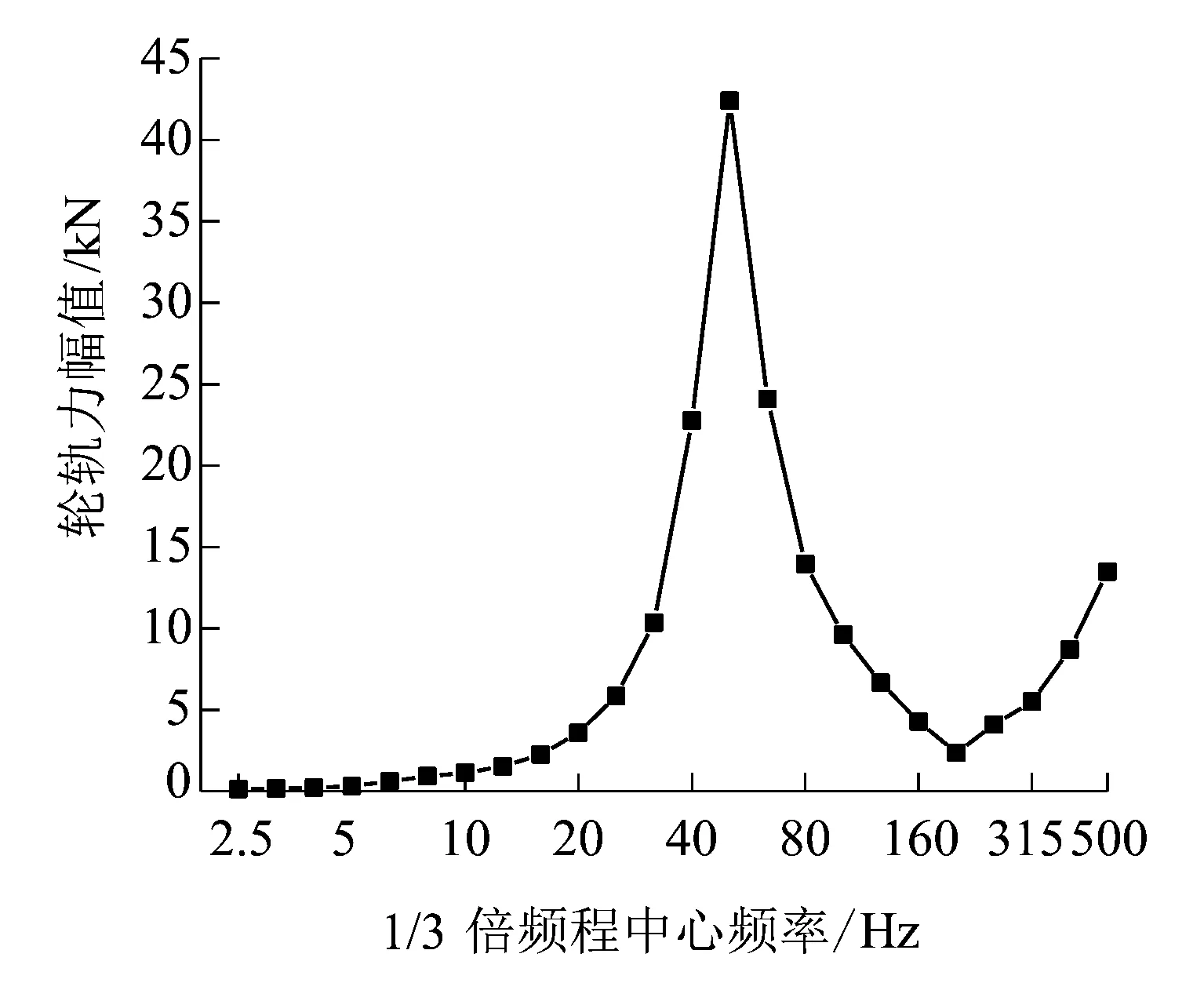
(b)1/3倍频程轮轨力

2.2 箱形梁计算模型

利用VAOne软件分别建立32 m双线箱形梁FE、FE-SEA混合和SEA模型。高架箱形梁建造所使用的混凝土强度等级为C55，其物理性质参数见表3。

表3 混凝土物理性质参数

在梁体结构支座处用点约束模拟简支边界条件[4]。仿真计算的箱形梁模型横截面及激励施加在桥梁的位置情况如图6所示，激励以最不利的方式加载，即施加在箱形梁正中部位置。

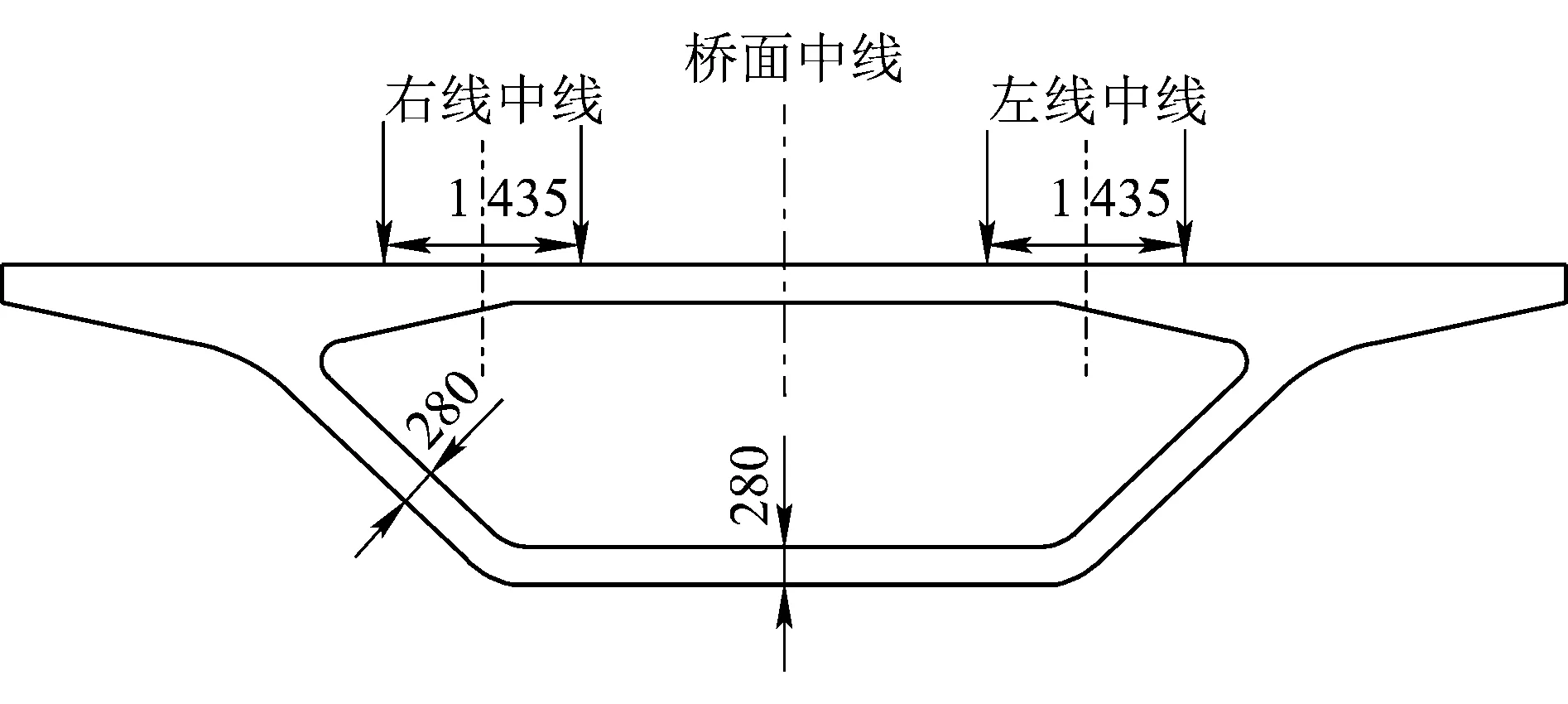
(a)跨中截面

(b)激励加载示意

3 箱形梁振动响应分析

3.1 振动响应分析

本文激励计算采用德国不平顺谱(波长为0.07～30 m)，车速为140 km/h，箱形梁的振动与声辐射分析频率为2.5～500 Hz。计算连续频率荷载和1/3倍频程荷载作用下桥梁各板单元的振动响应，如图7所示。由图7可以看出桥梁各板振动响应均在50 Hz处到达最大值。由于本文关注的桥梁结构噪声与桥梁结构振动能量分布有直接关系，1/3倍频程的计算方式能够很好地反映能量的分布，且1/3倍频程谱线少、频带宽，所以在后续的仿真计算分析过程中均采用1/3倍频程计算方式[11]。

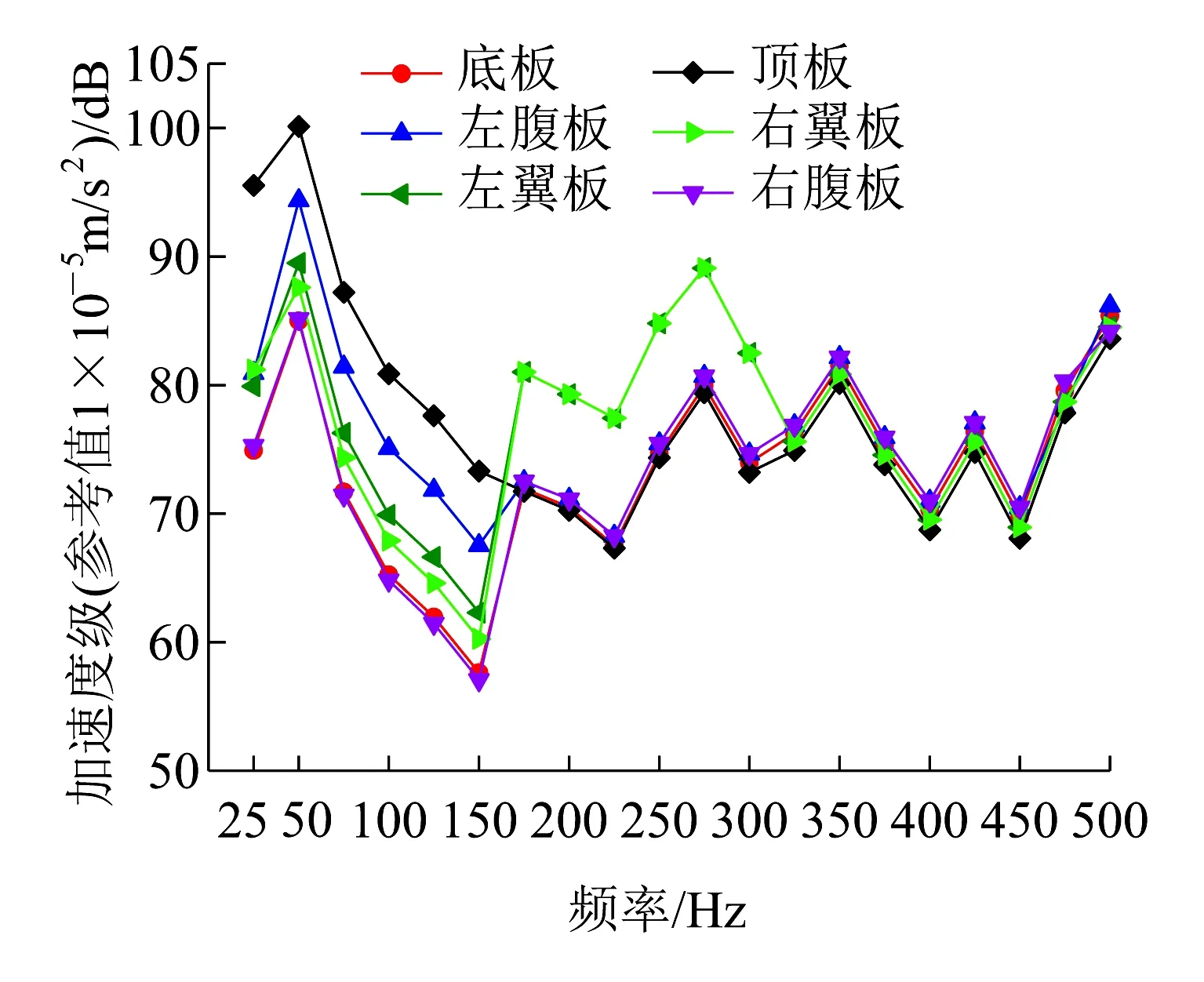
(a)连续频率荷载

(b)1/3倍频程荷载

由图7(b)可知：小于6.3 Hz频段内箱形梁整体振动明显，峰值出现在4～5 Hz。在2.5～500 Hz频段内左右腹板振动几乎一致，左右翼板振动规律相同。箱形梁各板单元产生的振动响应最大幅值均在50 Hz处，振动响应最大幅值对应的频率与频域内轮轨力最大值对应的频率吻合。箱形梁的左右翼板、左右腹板、底板、顶板单元中点的最大加速度级分别为120.6、117.9、118.3、116.9、113、116 dB。在整个分析频段，箱形梁产生振动响应明显的频段为40～80 Hz，因此在40～80 Hz频段内首先应考虑采取减振措施，达到减振的目的；在整个分析频段内，最大加速度级出现在左翼板，这是由于翼板宽度和厚度均较小，且荷载作用在左侧。如图7所示，在2.5～50 Hz频段内，各个板振动加速度级几乎在5、20、50 Hz均出现峰值，这3个频带为主要的减振频带；10～40 Hz和100～200 Hz频段内，顶板产生的振动加速度级比其余板单元大，即顶板起主要的振动作用，因此频段内对顶板减振能为整体减振带来良好的效果；在200～500 Hz频段内，各板单元的振动加速度级逐渐增大，左右翼板和顶板增加较明显，因此应将其作为主要的减振对象。

3.2 模型验证

为验证本文箱形梁模型的准确性，在相同工况下进行实地测试。车速为140 km/h，测得箱形梁顶板振动响应的最大值为112.9 dB，通过软件进行仿真计算分析得到理论值为111.5 dB，可以认为：实地测量值与理论计算值相差较小。由于仿真计算分析中不包括铁路轨道及桥墩等其他结构因素的间接减振作用，因此远声场点(距离左线中线25 m)的声压辐射响应模拟数值比实地测量数值偏大，如图8所示。由桥梁振动及远声场点声压级的模拟值与现场实测值对照可知本文模型是正确的。

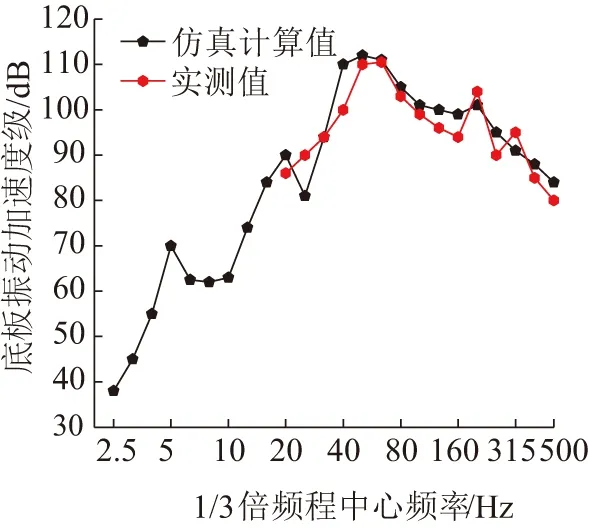
图8 底板加速度仿真值与实测值对比

将本文仿真计算分析的效率与文献[12]进行比较，结果见表4，可以看出：本研究模型在保证预测准确度的前提下，计算效率也有大幅度提升。

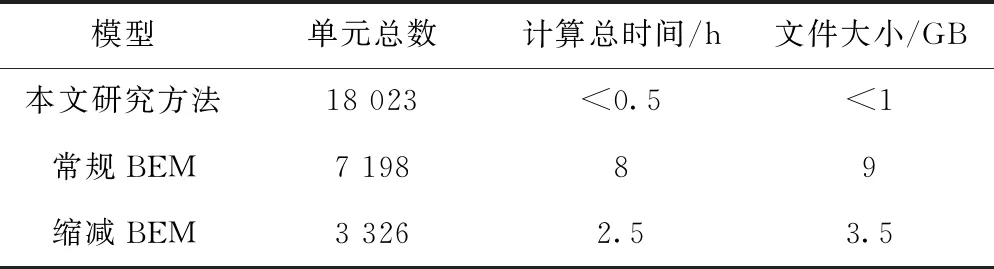
表4 计算方法效率对比

3.3 振动功率与能量分析

振动功率L由各子系统的阻尼及相邻子系统间耦合，由轮轨力输入能量w根据L=lg(w/wref)(wref=10-12W)计算求得。箱形梁整体振动功率损失如图9所示，其振动功率级损失出现在整个仿真分析的频段内。在2.5～6.3 Hz频段内，箱形梁产生的振动功率级损失随着频率增加呈现逐渐下降的趋势；在6.3～63 Hz频段内，箱形梁产生的振动功率级损失值约为12.9～18.4 dB；在63～500 Hz频段内箱形梁产生的振动功率损失随着频率的增加而上升。

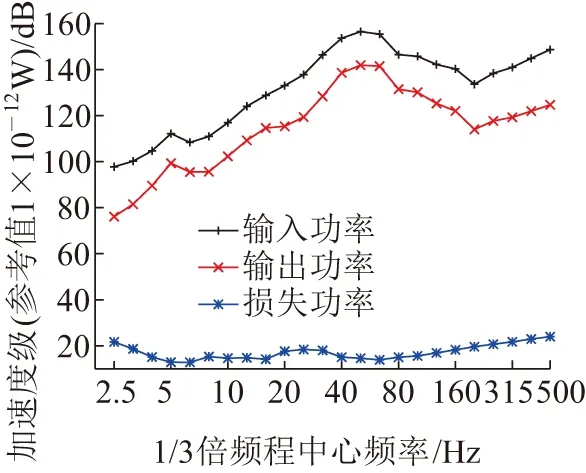
图9 箱形梁振动功率损失

利用FE-SEA混合方程计算得到箱形梁SEA子系统产生的共振能量，FE子系统的求解则是通过将子系统局部质量与箱形梁的振动速度结合得到。计算得到的箱形梁振动能量级如图10所示。由图10可知：箱形梁各板单元产生的振动能量级随频率的变化与其产生的声压辐射响应规律大致相同，在2.5～500 Hz频段内，5 Hz和50 Hz处箱形梁产生的振动能量最大。对箱形梁进行模态分析，如图11所示，图11中颜色由红至蓝，代表振动能量由高到低。将箱形梁1阶振型与40阶振型对比可知，在50 Hz处箱形梁各个板的局部振动明显大于5 Hz处对应的整体振动。将40阶振型与239阶振型对比可知，200 Hz对应的局部振动小于50 Hz处的局部振动。这与图10箱形梁振动能量级的结果基本一致。

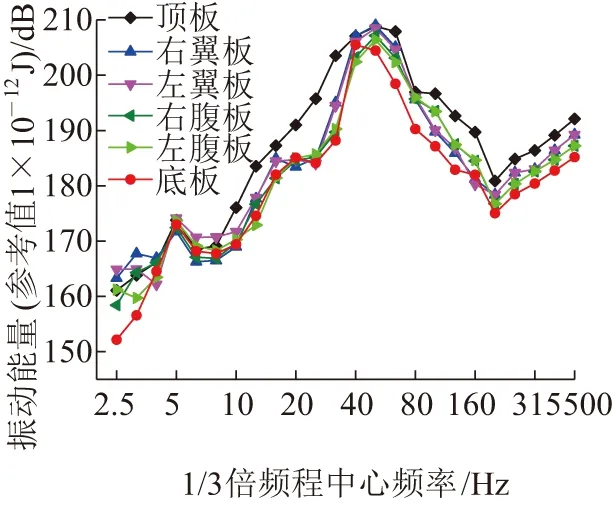
图10 箱形梁各板单元振动能量级

图11 箱形梁振型

4 箱形梁结构噪声影响分析

4.1 声场点布置

分析箱形梁各板单元在近场点(各板单元中心垂直向外0.3 m范围)的噪声声压辐射响应分布规律，同时分析箱梁各板单元结构在场点处的声压辐射响应，在箱梁跨中设置考察场点M1、M2和M3，如图12所示。其中M1和M2到桥面的竖向距离分别为1.2 m和3.5 m，M3与地面的竖向距离为1.5 m，3个场点距左线中线的水平距离均为25 m。

图12 远场位置示意(单位：m)

4.2 仿真结果分析

图13为梁体各板单元在近场点的声压辐射响应值。从图13可以看出：各板单元声压辐射响应和振动响应最大值均出现在50 Hz处，这是因为轮轨力最大幅值对应频率也为50 Hz；近场点箱形梁结构声辐射响应较明显的频段主要为40～80 Hz。在近场点，顶板的声压辐射响应出现最大值128.5 dB。在2.5～50 Hz频段内，随着频率的增加，各板单元声压级总体呈逐渐上升趋势。在50～200 Hz频段内各板单元声压级总体上逐渐下降。但在200～500 Hz频段内，各板单元声压级呈上升趋势，且顶板占据一定优势，其最大值为98.0 dB，小于2.5～50 Hz频段段内的最大值。在整个分析频段内，底板最大声压级为112.9 dB；在4～16 Hz频段内，底板产生的声压仅次于顶板。在整个分析频段内，顶板声压级占据明显的优势。翼板的振动响应较大，但是由于翼板相对其他板单元结构尺寸较小，因此翼板所产生的结构声压辐射响应比其他各板单元小。左右翼板声压级最大幅值分别为114.6、115.9 dB，在5～10 Hz频段内左翼板声压级比右翼板大，在100～500 Hz频段内，左右翼板声压级几乎一致。这是由于左右翼板宽度和厚度均较小，在低频时，靠近激励一侧的结构产会生较大的声压，高频时，结构的对称性会使相互对称部位产生的声压几乎一致。

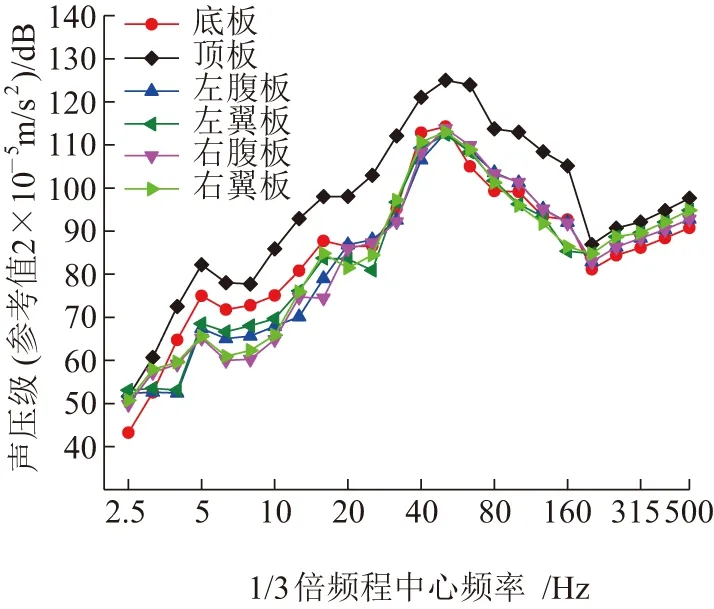
图13 近场点声压级

桥梁结构的3个远场点声压值如图14所示，可以看出，与桥梁水平距离相同、高度不同的远场点声压值基本相同。

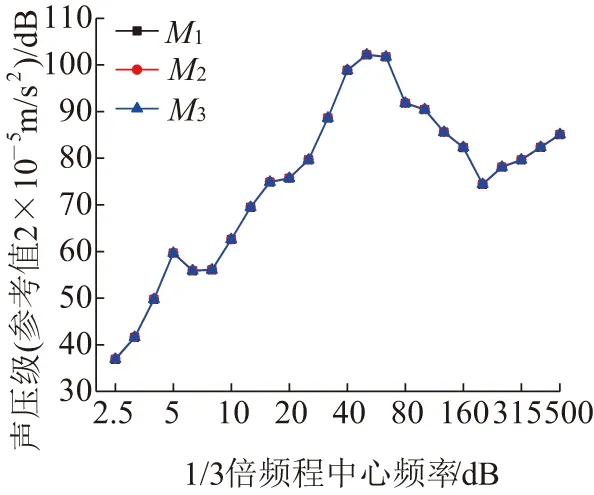
图14 远场点声压级

4.3 声压贡献量

通过仿真计算分析箱形梁各板单元的声压贡献量，能够指导选择合适的降噪措施。通过仿真分析计算得到箱梁各板单元使远场点M1、M2、M3产生的声压辐射响应，结果如图15所示，由于M1、M2、M3的声压辐射响应规律相同，将3点的变化情况用1幅图绘出。进一步分析计算，得到箱形梁梁体单元在远场点M1、M2、M3辐射的总声压值，通过理论计算得到箱形梁各板单元对3个远场点的声压贡献量，计算结果见表5。

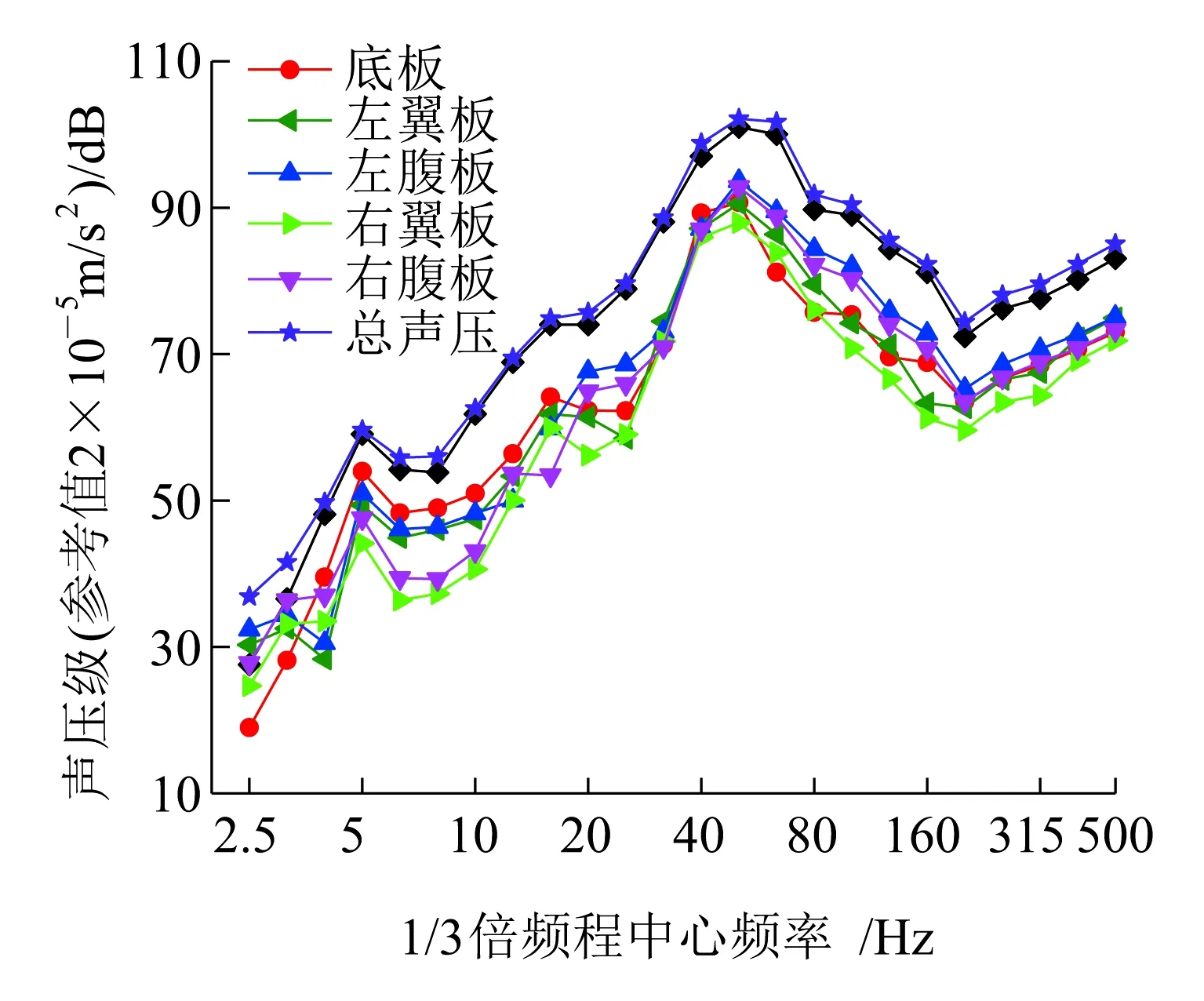
图15 桥梁整体及各板在远场点M1、M2、M3处产生的声压级

以远场点M2为例，图15(b)为仿真计算出的远场点M2处的声压辐射响应结果，可以看出，M2的总体声压辐射响应峰值出现在5 Hz和50 Hz处。由表5可以看出顶板对场点M2的声贡献量最大，左腹板的声贡献量次之，右翼板声贡献量最小。

表5 远场点声压级及各板单元贡献量

5 结论

(1)在2.5～500 Hz频段内分别建立FE、FE-SEA混合与SEA模型，进一步仿真计算箱形梁结构在垂向轮轨力作用下的振动及噪声响应。

(2)32 m双线简支箱形梁在50 Hz处局部振动响应幅值达到最大，加速度优势频率集中在5～50 Hz。在2.5～500 Hz频段内，顶板的声辐射响应明显大于其他板单元，但是振动响应最大值出现在左翼板。

(3)箱形梁顶板单元在远近声场点的声压贡献量均比其他板单元大，在整个分析频段内顶板产生的声压起主导作用，因此在降低噪声辐射响应方面应首先考虑对箱形梁顶板采取必要的措施。

(4)箱形梁产生的振动响应以及对远近声场点声压辐射响应影响较明显的频段为40～63 Hz，通过计算得到轮轨力最大幅值频率也在40～63 Hz，因此应在该频段重点采取必要措施，达到对箱形梁的减振降噪目的。

(5)箱形梁的振动功率级损失值范围为12.9～18.4 dB。箱形梁振动能量的最大幅值频率为50 Hz，各板单元的振动能量级由大到小为顶板、翼板、腹板。

(6)本文模型避开了FE确定性方法在高频段计算量大及SEA在低频段精度差的缺点，解决目前箱梁振动噪声计算效率与精度的矛盾，提高了预测精度及计算效率，扩大了桥梁结构振动与结构噪声频谱特性研究的频域范围。