轴系纵振诱发的螺旋桨轴承力特性研究

邹冬林，冷子珺，徐江海，塔 娜，饶柱石，2

（1a.上海交通大学振动、冲击、噪声研究所；b.机械系统与振动国家重点实验室，上海 200240；2.高新船舶与深海开发装备协同创新中心，上海 200240）

0 引 言

由于海洋流场的不均匀性、轴系倾斜以及船舶绕流效应等因素，螺旋桨通常工作在不均匀来流场中，这使得螺旋桨叶片表面产生不断变化的激励力。螺旋桨激励力传递至船体将引起船体振动，不利于船舶的正常稳定运转。对于民船而言，船体振动会导致船体结构的疲劳损害，同时也影响舱室内精密仪表的可靠性。而且过大的噪声容易刺激乘客与船员，使之烦躁不安，降低船舶的舒适性。对于测量船而言，由于其需要借助水声设备对海洋资源进行探测，因此其自身的振动噪声水平需要严格控制，以保证各种测量设备能在安静的水中正常工作。对于军舰及潜艇等而言，噪声是其性能及生命力的体现指标之一。因为一方面船体振动辐射的低频线谱噪声很容易被敌方声呐探测，从而暴露位置成为敌方打击的目标；另一方面，因为过大的噪声也干扰自身声呐的测量精度，从而失去制敌先机。而近几十年来，声呐探测技术得到了很大发展，这对潜艇等舰船的声隐身性能提出了更高的要求。因此减少螺旋桨激励力或者抑制螺旋桨激励力向船体传递的效率一直都是国内外研究的热点问题。螺旋桨激励力向船体传递的途径主要分为两种：一种是通过周围的流体直接传递到船体，称之为表面力；另一种是通过桨、转轴及轴承传递至船体，称之为轴承力。有研究表明，相比于表面力，轴承力是船体振动更主要的因素[1]。因此，对螺旋桨轴承力特性进行研究，掌握轴承力的生成机理，将能为船体减震降噪技术的有效展开提供理论指导。

目前，国内外学者对螺旋桨轴承力特性做了大量研究。如Liu 等[2]利用面元法计算了吊舱推进器处于各种方位角时的轴承力特性，并与实验结果进行了比较；Liefvendahl等[3]用大涡模拟方法（LES）计算了处于潜艇后方的螺旋桨轴承力特性，并讨论了其周期性问题；Dubbioso 等[4]利用雷诺平均法（RANS）模拟了螺旋桨倾斜时的轴承力特性；Ortolani 等[5-6]利用CFD 方法研究了船舶的机动运行对其后螺旋桨轴承力特性的影响规律；Bugalski和Szantyr[7]针对船舶艉部的不均匀尾流场，开发了四种尾流场改进装置，利用升力面理论研究了改进装置对螺旋桨轴承力特性的影响。国内也有不少学者做过相关研究，比如谭廷寿等[8]介绍了利用面元法计算螺旋桨轴承力的详细过程；叶金铭等[9]对比研究了拟定常方法、升力线理论及CFD方法在螺旋桨轴承力计算上的优缺点，并讨论了侧斜与桨叶数目对螺旋桨轴承力的影响，他们还基于CFD 方法讨论了螺旋桨加工误差对其轴承力特性的影响规律[10]；舒敏骅等[11]研究了Fluent 软件中的动网格法在计算螺旋桨轴承力方面的精度，并与已有实验结果对比；Wei等[12]利用RANS方法研究了处于潜艇后方的螺旋桨的轴承力特性，并研究了螺旋桨轴承力引起的艇体声辐射；陈如星等[13]利用CFX软件分析了桨-舵间的相互作用对螺旋桨轴承力特性的影响。

综上所述，上述针对螺旋桨轴承力的研究中，均假设螺旋桨从桨毂处断开，忽略轴系振动的影响。由于螺旋桨随轴系振动，将诱发螺旋桨和伴流场耦合面间的流体振荡。即使来流场是均匀的，这种流体振荡同样会使螺旋桨产生轴承力。根据相关文献资料，由于船体和轴系振动诱发的螺旋桨和伴流场耦合面的流体振荡，可使螺旋桨轴承力产生的低频声辐射增加若干个分贝。由此可见不能忽略轴系振动对螺旋桨轴承力的影响。

因此，针对上述研究不足，本文重点研究由轴系振动诱发的螺旋桨轴承力特性。为了区分开来，本文将由不均匀流场导致的螺旋桨轴承力称之为主轴承力（这类轴承力也是目前国内外学者所关注的），将由轴系稳态振动诱发的螺旋桨轴承力称之为附加轴承力或者二次轴承力（这类轴承力目前国内外研究很少）。因此，总的螺旋桨轴承力由这两部分合成。这里采用轴系稳态振动来定义附加轴承力的原因是因为螺旋桨附加轴承力的产生本身就是一个不断耦合变化直至稳态的过程。比如不均匀流场产生螺旋桨主轴承力，引起轴系振动，进而产生附加轴承力，附加轴承力与主轴承力合成后产生新的轴系振动，进而又产生新的附加轴承力，如此重复直至稳态振动。由附加轴承力的产生过程也可以知道螺旋桨轴承力和轴系振动是相互影响、相互耦合的，彼此形成反馈机制并且可能存在增强效应。

1 数学模型

目前，针对螺旋桨轴承力的数值计算方法有很多，包括基于势流理论和基于Navier-Stokes 方程两大类。其中基于势流理论的面元法兼具计算精度与计算效率的优点，是一种高效可靠、快速经济的方法，因而被广泛使用。这类面元法基本都是基于Morino和Kuo[14]、Lee[15]和Hsin[16]的研究工作发展而来，主要计算不均匀进流场引起的螺旋桨主轴承力。当考虑螺旋桨跟随轴系做复杂空间振动时，需要对这类面元法做适当修改。因此，本文首先结合转子动力学的基本理论，建立既能考虑非均匀来流，又能考虑做任意复杂振动的螺旋桨轴承力预报数学模型，从而进一步推广传统的轴承力预报模型。

限于篇幅，本文简单介绍这一改进的轴承力预报数学模型，详细推导过程见文献[17]。要建立随轴系振动的螺旋桨轴承力预报数学模型，需要解决三个问题：一是建立轴系做复杂空间振动的数学模型，二是建立具有复杂空间振动固体的物面边界条件，三是建立时变的尾涡数学模型。下面分别介绍。

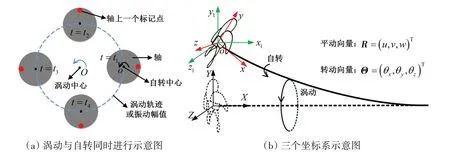
图1 轴系振动与三个坐标系示意图Fig.1 The schematic of shaft vibration and three coordinate systems

在轴承力计算中，需要考虑从叶片随边泄露出的尾涡影响。对尾涡的建模主要考虑尾涡的强度和尾涡的形状。对于传统的桨毂不随轴系振动的螺旋桨，尾涡的形状通常假定为螺旋面，即线性尾涡。尾涡泄露的强度通常按Morino 库塔条件[14]或压力库塔条件处理[15-16]。而对于桨毂随轴系做任意空间振动的螺旋桨，由于其运动轨迹复杂，使得不同时刻桨叶随边的位置也不一样，从而影响尾涡的形状。因此需要对尾涡进行合理建模，以便能考虑不同时刻螺旋桨位置变化对尾涡几何形状的影响。

本文假设尾涡的泄露是一个随时间变化的过程，如图2 所示。在初始时刻，假设螺旋桨静止，此时没有尾涡泄露。在Δt时刻，螺旋桨往前移动一个距离，此时泄出第一个尾涡，其强度用Morino 库塔条件计算，即

图2 尾涡泄露过程示意图Fig.2 Process of vortex-shedding

式中，ΔΦ(rT,t)为t时刻叶片半径rT的随边处泄露的尾涡速度势，Φ+(rT,t)为t时刻叶背（吸力面）随边处的速度势，Φ-(rT,t)为t时刻叶面（压力面）随边处的速度势。在2Δt时刻，螺旋桨继续以Vin运动一个距离，此时泄出第二个尾涡，强度仍然按式（2）确定。而Δt时刻泄露的尾涡其强度保持不变，在原地运动并发生收缩、卷曲等变形。以此时间类推，从而尾涡的泄露是一个连续的过程。

泄露的尾涡不能受力，由库塔-茹科夫斯基定理可知，泄露尾涡的速度必定与当地的流场速度平行，即尾涡片必定按当地的流线运动。因此，在OXYZ坐标系中，泄露的尾涡在每个时间步运动的距离为

螺旋桨做任意复杂振动后的扰动速度势Φ(t)仍然满足拉普拉斯方程，由于螺旋桨几何形状很复杂，因此很难求其解析解，通常只能求取数值解。为了获得其数值解，需要将螺旋桨表面（包括尾涡面）划分成一系列小的双曲四边形单元。由于采用时变尾涡数学模型，因此尾涡生成的位置及总的数目均在不断变化。设泄露尾涡面元的展向数目为nr，弦向数目由时间总步数nt决定。比如在it个时间步，弦向泄露共it个尾涡面元，其中只有紧靠叶片随边的第一列面元强度未知，其它尾涡面元强度均已知，如图3所示。

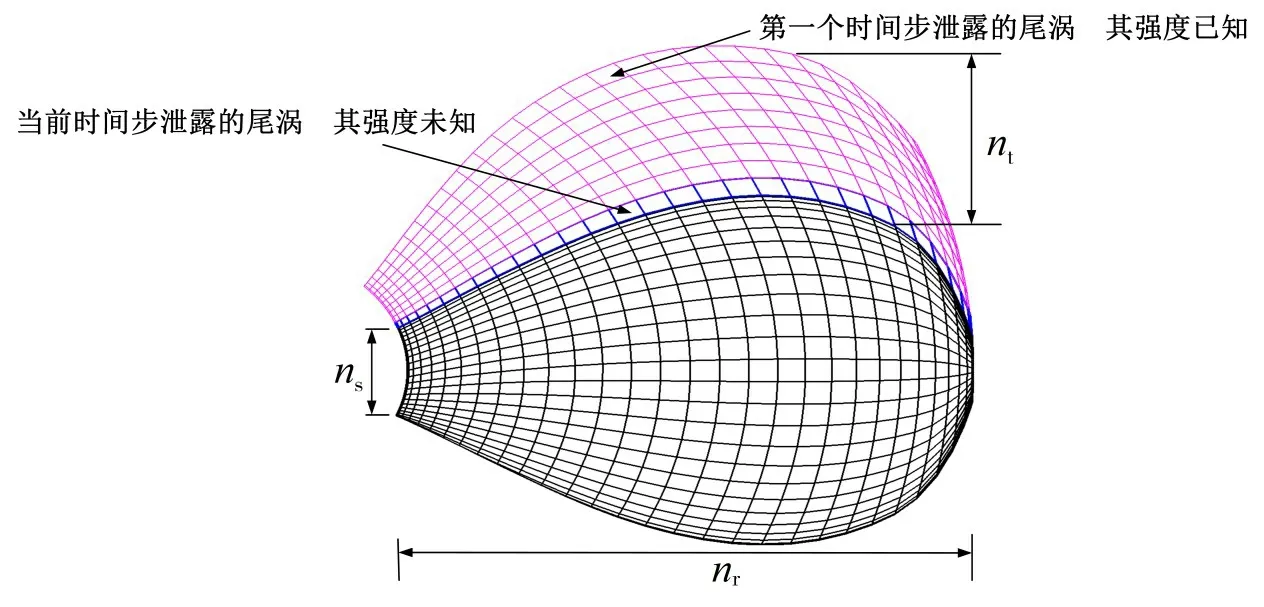
图3 螺旋桨及泄露尾涡面元分布Fig.3 Panel arrangement of propeller and wake

因此在第it个时间步，螺旋桨表面上的扰动速度势Φ(t)满足[17]

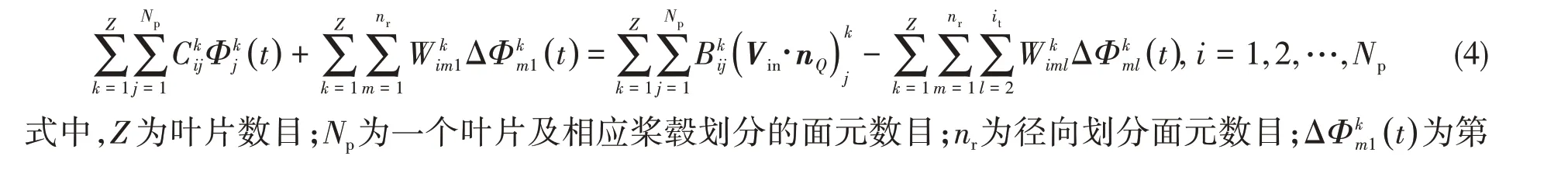
由此可知，式（4）右边各项均为已知量，方程可以求解。进一步写成矩阵形式如下：

整个求解流程如图4所示。在叶片呈刚性状态时，由于叶片几何形状不变，因此A只需在第一个时间步计算一次，后面的时间步不需重新计算。求出叶片上速度势分布后，可以进一步求出叶片表面的流体速度，再结合不定常伯努利方程即可求出叶片表面的脉动压力分布，从而可以求出螺旋桨轴承力，整个求解过程详见文献[17]。实际计算中，时间步数nt的选取要足够大，以保证计算结果呈周期变化。

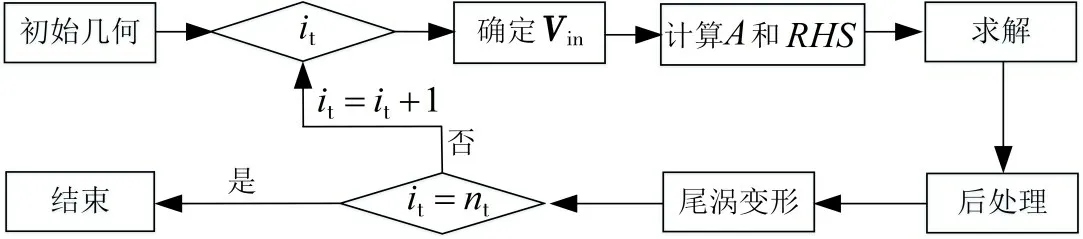
图4 求解流程图Fig.4 Flow chart of solution

2 仿真分析

尽管本文的轴承力预报模型可以考虑螺旋桨的任意复杂振动，但是本文侧重于研究轴系纵振诱发的螺旋桨附加轴承力特性。这是因为相比于螺旋桨横向轴承力，纵向轴承力是引起船体声辐射的最主要的原因[1]。以P4381螺旋桨为研究对象，P4381螺旋桨属于P438X系列螺旋桨的母桨，5叶片无侧斜，其详细几何参数见文献[17]。假设螺旋桨纵向振动（或者轴系末端的纵向振动）为δx=Asin( )ωt，其中ω既是轴系的振动频率，也是螺旋桨的自转角速度。计算中设ω为180 r/min，假设轴系纵向振动幅值为1 mm，根据简谐振动理论，轴系纵向振动速度大约为0.0188 m/s。同时假设螺旋桨直径为5 m。计算时，步长取为Δθ=1°，一共计算6圈，直至结果呈周期变化，取最后一圈的数据做分析。

图5为计算的推力与扭矩系数变化过程，从图中可以看出螺旋桨运动瞬时，推力和扭矩系数都有一个急剧变化，再慢慢稳定呈周期变化。

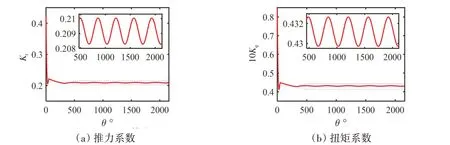
图5 脉动推力系数与扭矩系数Fig.5 Pulse thrust and pulse torque coefficients

图6 为螺旋桨单个叶片和所有叶片合成后的纵向与扭转方向上的附加轴承力，从该图中可以看出：（1）轴系纵向振动会产生纵向附加轴承力，同时由于叶片的空间扭曲，轴系纵向振动同时使螺旋桨产生扭转附加轴承力；（2）轴承力频率成分与轴系振动频率相同，且各单个叶片上产生的纵向与扭转附加轴承力幅值与相位均相同，这与不均匀流场导致的主轴承力各叶片间存在恒定相位差有所不同；（3）在轴系纵向振动振幅为1 mm，频率为3 Hz时，纵向附加轴承力约占静推力（1058 kN）的4.6‰，这与不均匀流场产生的主轴承力在同一个数量级，因此不能被忽略。

图6 纵向与扭转方向上的附加轴承力Fig.6 Longitudinal and torsional bearing force

为了进一步研究轴系纵向振动幅值与频率对螺旋桨纵向附加轴承力的影响，本文对P438X 系列螺旋桨进行研究。计算两组工况：一组是纵向振动频率不变（取为3 Hz，螺旋桨旋转速度也取为180 r/min），改变纵向振动幅值（依次取为10 μm、200 μm、400 μm、600 μm、800 μm 及1000 μm），计算螺旋桨纵向附加轴承力与纵向振动幅值间的关系；另一组是纵向振动幅值不变（取为1000 μm），改变纵向振动频率（依次取为0.5 Hz、1 Hz、1.5 Hz、2 Hz、2.5 Hz 及3 Hz），计算螺旋桨纵向附加轴承力与纵向振动频率间的关系。此时，螺旋桨旋转速度也与纵向振动频率一致，且保证进速系数J恒为0.889。

图7 为P4381 桨纵向附加轴承力与轴系纵向振动幅值及频率的关系曲线。类似地，图8～10 分别为P4382桨、P4383桨及P4384桨的纵向附加轴承力计算结果。从这几个图可以得出：（1）螺旋桨纵向附加轴承力与轴系纵向振动幅值成正比关系；（2）螺旋桨纵向附加轴承力与轴系纵向振动频率的平方成正比关系；（3）侧斜角越大，轴系纵向振动产生的纵向附加轴承力则越小。

图7 P4381桨纵向轴承力与纵向振动幅值及频率关系Fig.7 Relation of axial bearing force with axial vibration amplitude and frequency for P4381

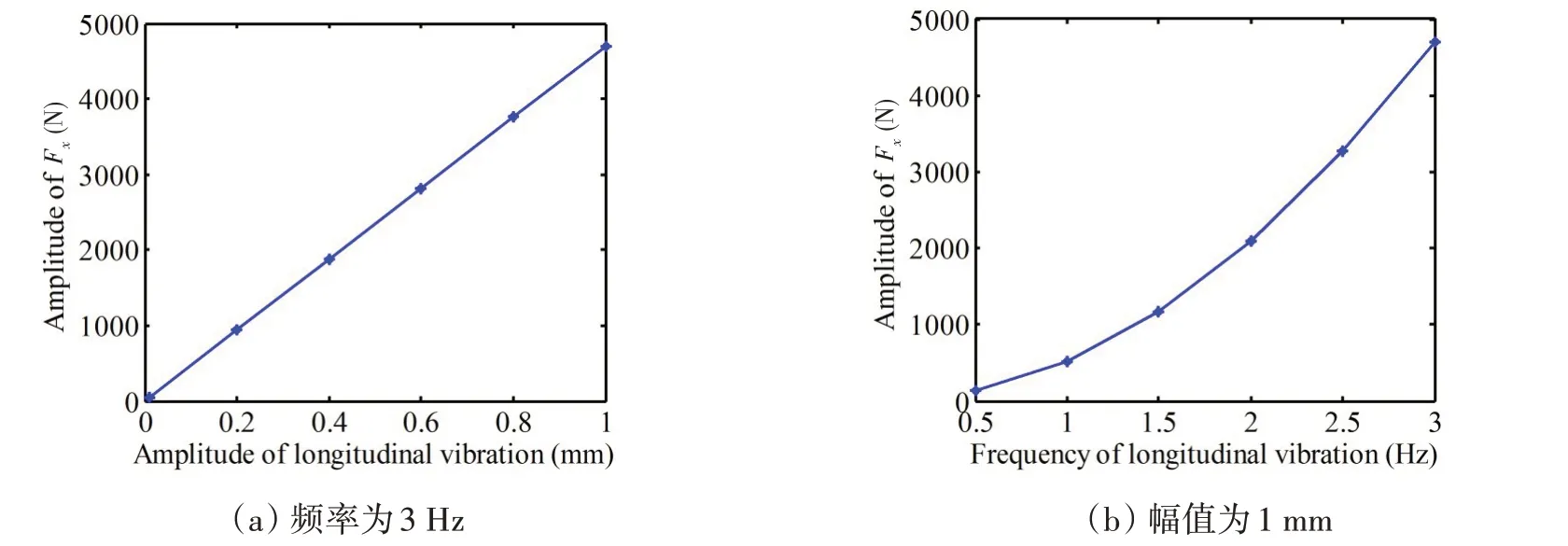
图8 P4382桨纵向轴承力与纵向振动幅值及频率关系Fig.8 Relation of axial bearing force with axial vibration amplitude and frequency for P4382

图9 P4383桨纵向轴承力与纵向振动幅值及频率关系Fig.9 Relation of axial bearing force with axial vibration amplitude and frequency for P4383

图10 P4384桨纵向轴承力与纵向振动幅值及频率关系Fig.10 Relation of axial bearing force with axial vibration amplitude and frequency for P4384

由于本文计算参数中，轴系纵向振动速度很小（这也符合工程实际），此时尾涡的非线性效应很弱，因此轴系振动幅值与纵向附加轴承力幅值近乎呈正比关系。可以预见，如果进一步增加轴系振动速度（增大振幅或者振动频率），则将会产生较强的非线性效应，而且此时桨叶表面也将有流动分离现象，第（1）与第（2）结论将不成立。但这已不符合工程实际，超出了本文的研究范畴。

进一步地，本文对一系列叶数、直径、盘面比、螺距比不同的螺旋桨进行了计算，发现轴系纵向振动诱发的螺旋桨纵向附加轴承力与这些参数有关，因此可以将该轴承力表示成这些参数的表达式。结合量纲分析，该估计公式可以表示为

式中，Fx为轴系纵向振动诱发的螺旋桨纵向附加轴承力幅值，单位为N；A为轴系纵向振动幅值，单位为m；ω为轴系纵向振动频率，单位为rad/s；ρ为流体密度，单位为kg/m3；Z为螺旋桨叶片数；D为螺旋桨直径，单位为m；P/D为叶面0.7R半径处的螺距比；Ae/Ao为叶面盘面比；a1至a6为系数。通过对大量螺旋桨计算后拟合分析（一共计算了57个螺旋桨），得到了这些系数的估计值,如表1所示。

表1 各系数取值范围及推荐值Tab.1 Range of these coefficients and recommended values

利用该估计公式，本文对几个常用的螺旋桨进行了估计。假设螺旋桨直接均为5 m，轴系纵向振动幅值为1 mm，纵向振动频率为3 Hz。图11 为计算值与公式估计值的比较，从图中可以看出该公式对有的螺旋桨估计精度很高，相对误差仅为1.46%（P4679 桨），有的相对误差较大，达到19.4%（P4119桨）。由于该估计公式提出时兼顾了许多螺旋桨的几何特征，因此其精度对某些螺旋桨误差可能很大，而对某些螺旋桨误差可能很小。但不管如何，该公式可以为实际工程中纵向附加轴承力提供初步预估值。上述估计公式中没有考虑侧斜角的影响，考虑侧斜角后，纵向附加轴承力应减少2%～10%。

图11 纵向附加轴承力估计值与计算值比较Fig.11 Comparison of bearing forces between the calculation and estimation

3 实验验证

实验验证一方面是为了验证本文的螺旋桨轴承力预报模型的准确性，另一方面是为了验证纵向振动诱发的螺旋桨轴承力特性。限于篇幅，本文对实验只做简单介绍，详细过程见文献[17]。本实验在上海交通大学机动学院与船建学院共同搭建的重力式水洞桨-轴振动实验平台上进行，其简图如图12所示。

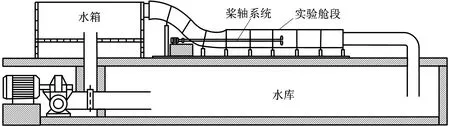
图12 重力式水洞示意图Fig.12 Sketch of the gravity tunnel

桨-轴系统上安装有纵向激振器，能使转轴产生纵向振动。实验时，在激振器附近布置加速度传感器，以测量该处的纵向加速度，如图13所示。由于加速度传感器随转轴一起旋转，因此加速度数据通过网络传输给电脑。同时在轴系末端桨毂上也布置加速度传感器（实验对象为P4381 螺旋桨），以测量桨毂的纵向加速度，也即轴末端的纵向加速度，如图14所示。同样，由于该加速度传感器随螺旋桨旋转，同时又处于水下密闭环境中，因此采用滑环装置将信号引出来，并同时对加速度传感器及滑环装置都做防水处理。

图13 加速度传感器布置图Fig.13 Arrangement of acceleration transducers

图14 桨毂上加速度传感器及滑环装置Fig.14 Acceleration transducer and slip ring at the hub

当激振器给轴系施加纵向激励力时，会引起螺旋桨纵向振动，从而进一步在螺旋桨上产生附加激励力施加在转轴上，该附加激励力与纵向激振器的激励力合成后，进一步产生新的螺旋桨纵向振动，如此反复直到稳定。通过测量激振器处及桨毂处的纵向加速度，可以推导出轴系纵向振动与其诱发的附加激励力（轴承力）间的相互关系。如图15 所示，设激振器产生的纵向激励力为F1ej()2πft+φ1，由此导致的螺旋桨附加轴承力为，其中f为激励频率。假设测点1 处测得的加速度响应可表示为，测点2 处测得的加速度响应可表示为。因此可以推得

图15 测量原理图Fig.15 Diagram of measurement principle

式中，Hij为测点j处激励时，测点i处的加速度频响函数，可以通过模态实验获得。由式（7）可知：

由此可见，通过式（8）可以很方便求出由于轴系纵向振动诱发的螺旋桨附加轴承力的幅值F2。实验时，螺旋桨旋转速度为480 r/min，来流速度为1.5 m/s。

3.1 附加轴承力与振动幅值关系测量

为了研究轴系振动幅值与螺旋桨附加轴承力幅值间的相互关系，实验中激励频率f保持不变，通过改变信号发生器的输出电压值（该电压输入功率放大器中）来控制激振器的激振力大小，从而使轴系末端产生不同的纵向加速度A2，观察螺旋桨附加激励力F2与A2间的关系。实验时，信号发生器的输出电压依次为7.0 V、7.5 V、8.0 V、8.5 V、9.0 V、9.5 V，激励频率f分别取为103 Hz 与193 Hz 两种工况。

将测得的加速度代入式（8），即可以求出螺旋桨附加轴承力幅值F2。本文将F2除以ρR4n2（R为螺旋桨半径，n为转速）进行无量纲化，测量结果如图16所示。进一步地，本文对测量的结果进行了一次线性拟合。从拟合曲线与原测量曲线可以看出两者基本上重合，从而表明螺旋桨附加轴承力与轴系纵向振动位移幅值呈正比关系（尽管横坐标为加速度数据，但是因为激励频率不变，因此也可以等效认为是振动位移幅值）。

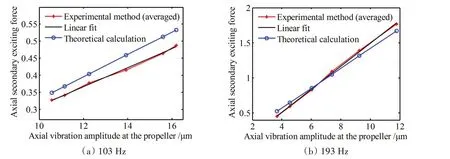
图16 螺旋桨附加轴承力与螺旋桨处振动幅值关系曲线Fig.16 Experiment data of propeller bearing force and vibration amplitude

同时，本文将所测得的螺旋桨处纵向位移代入本文的理论计算模型中，比较理论计算值与实测值间的差异。103 Hz激励时，理论计算值与测量值间最大误差为9.25%；193 Hz激励时，理论计算值与测量值间最大误差为7.83%。造成两者之间差异的主要原因有：（1）对于理论计算值，由于采用势流理论，忽略了流体粘度的影响，其计算结果本身就有一定的误差。同时本文的模型忽略导边涡分离的影响，这在高频时尤为明显。（2）对于测量值，由于加速度信号本身的测量误差以及加速度频响函数测量误差，均会导致测量结果偏离准确值。同时轴系转动时，由螺旋桨不平衡力引起的横向振动对测量结果同样会有影响。

3.2 附加轴承力与振动频率关系测量

为了研究轴系振动频率与螺旋桨附加轴承力幅值的相互关系，本实验需在保证螺旋桨处纵向振动位移Aˉ2不变的同时，不断改变激励频率f，观察f与F2间的关系。但是，由于实际测试中无法保证不同频率下轴系末端螺旋桨处的振动位移相等，因此将螺旋桨附加轴承力F2按螺旋桨处纵向振动位移Aˉ2做归一化，观察f与F2/Aˉ2间的关系（纵向振动位移Aˉ2由纵向振动加速度A2换算得出，单位为μm）。这是因为前文已经得出螺旋桨轴承力F2与螺旋桨处纵向振动位移Aˉ2间成正比关系，因此这种处理方式是合适的。在验证螺旋桨附加轴承力与轴系振动频率间关系时，为了避免转频及其倍频、叶频及其倍频的干扰，将激励频率f取为11 Hz、43 Hz、73 Hz、103 Hz、133 Hz、163 Hz和193 Hz，信号发生器输出电压依次取为7.0 V 和9.0 V 两种工况。测量结果如图17 所示。进一步地，本文对测量的结果进行了二次函数拟合。从该图中可以看出测量值与拟合值重合很好，表明螺旋桨附加轴承力与纵向振动频率的平方成正比关系。

图17 螺旋桨附加轴承力与振动频率实验曲线Fig.17 Experimental results of propeller bearing force and vibration frequency

同样，将所测得的螺旋桨处纵向振动位移代入本文的理论计算模型以及估算公式中，比较理论计算值与实测值间的差异。可以看出，信号发生器输出电压为7.0 V 时，理论计算值与测量值间最大误差为10.46%；信号发生器输出电压为9.0 V 时，理论计算值与测量值间最大误差为9.89%。且最大误差都发生在193 Hz 处，表明高频时误差更大。三者间差异大的原因在3.1 节中已经阐述，此处不再赘述。

4 结论

本文利用面元法并结合转子动力学理论，建立了不均匀来流下做任意空间振动的螺旋桨轴承力预报的数学模型。利用该数学模型研究了轴系纵向振动与其诱发的螺旋桨纵向附加轴承力间的相互关系。通过对一系列半径、叶数、螺距比和盘面比不同的螺旋桨进行计算，拟合得到了螺旋桨纵向轴承力的估算公式，最后进行了实验测量。研究表明：（1）在轴系纵向振动振幅为1 mm，频率为3 Hz时，纵向附加轴承力约占静推力的4.6‰，这与不均匀流场产生的主轴承力在同一个数量级，因此不能被忽略；（2）当纵向振动速度不大时，螺旋桨纵向附加轴承力幅值与纵向振动幅值成正比关系，与振动频率呈平方关系。