界面对弹性球壳声辐射的影响分析

赵开琦，范 军，王 斌

（1.上海交通大学船舶海洋与建筑工程学院，上海 200240；2.高新船舶与深海开发装备协同创新中心，上海 200240）

0 引 言

水下潜器的辐射噪声既是被动声呐探测的重要信息源，又是影响水下潜器隐身性能的重要因素[1]。水下潜器所处的海洋信道为具有上下界面的水体环境。界面对声波的反射作用，不仅导致声波传播路径发生改变，而且经界面一次或多次反射，声波会入射到结构表面激发起弹性结构的几何散射和弹性散射（将经过界面二次和多次反射后入射到结构表面引起的声散射统称为多次散射），进而影响结构的声辐射特性及空间声场分布。处理波导中结构声辐射的一般方法是利用积分方程法或数值方法将结构振动和波导环境进行统一建模，得到的结果最为严格，但是当界面对结构的声源特性（表面振速和声压分布）影响可以忽略时，结构的声源特性可以用自由空间中的量近似，统一建模方法则会增加不必要的计算量，因此讨论界面对弹性结构声辐射的影响以及影响可以忽略的条件对研究界面附近或波导环境中水下潜器的声辐射特性尤为必要。

界面对水下结构振动和声特性的影响已有大量研究工作。研究方法主要分为数值法、实验法和解析法。于大鹏等[2]、Wu 等[3]采用有限元/边界元耦合方法对船舶在半无限域和有限水深域中的水下辐射噪声特性进行了讨论。Wu[4]提出了射线法和简正波法相结合的格林函数计算方法，建立了理想波导中声场计算的边界元方法。黎胜等[5]分别利用边界元法和半空间格林函数法讨论了界面对半空间内结构声辐射的影响。王斌等[6]利用有限元和边界元耦合方法对半空间中不同下潜深度下二维圆柱壳的振动特性和辐射声功率进行了讨论。但上述文献均基于半空间或波导中的格林函数，未考虑界面与结构之间的多次散射作用。Chen等[7]、商德江等[8]利用等效源法及有限元法建立了理想波导中结构振动和声辐射的数值模型，通过将壳体所处的局部波导环境进行整体有限元建模，在结果中包含了界面与结构之间的多次散射作用，进一步采用抛物方程法计算外部声场可提高模型的计算效率[9]，但对于界面对结构声源特性可以忽略的情况下，该方法仍存在不必要的计算量。Zou等[10]利用声弹性理论建立了理想波导中圆柱壳的声辐射数值模型，并进行了实验验证。Ergin 等[11]基于有限元和实验方法分析了有限潜深下圆柱壳的自由振动特性，指出自由液面会导致壳体的自由振动频率增大，但实验方法耗时耗力，相关报道较少。解析方法主要以基于Graf加法定理的虚源法为主，Gaunaurd 等[12]研究了界面附近球形目标的声散射特性，范威等[13-14]将该方法推广至平行和楔形理想波导中球形目标的散射特性研究；叶文兵[15]、Li 等[16]、Wang 等[17]、Guo 等[18]等对水面附近圆柱壳的振动和声辐射特性作了讨论，其重点关注界面对壳体振动状态的影响，其中文献[17]忽略了界面反射作用对实源表面振速的影响；白振国等[19]讨论了浅水域中二维圆柱壳的辐射声场的分布和衰减规律，利用辐射阻抗建立了振动位移与辐射、散射声压间的关系，使得界面对圆柱壳振动的影响更加明了。

本文以理想界面附近弹性球壳为研究对象，基于Graf 加法定理和虚源法建立了界面附近弹性球壳的振动和声辐射理论模型。球壳振动和外部声场分别用薄壳理论和简正级数表达，然后利用表面位移协调条件进行耦合求解，并推导了界面附近球壳辐射声阻抗、声压及声功率的解析表达式。讨论了辐射声阻抗、声压随界面类型、激励频率和下潜深度变化的物理规律。界面与结构之间的多次散射作用以声辐射互阻抗表示，可方便讨论考虑和忽略多次散射作用后的辐射声压及声功率。最后以声功率为评价指标，讨论并给出了界面对球壳声源特性的影响可以忽略的条件。

1 理 论

考虑轴对称简谐力激励情况，省略时间因子exp( -iωt)，界面附近弹性球壳的运动方程为[20]

式中：系数矩阵的元素l11～l22如下，

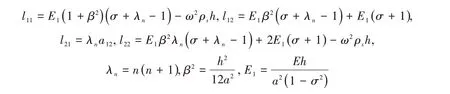
pn为壳体表面声载荷的勒让德展开系数；fRn为激励力的勒让德展开系数，满足

考虑界面为软边界和硬边界时，界面上声压分别满足p=0 和∂p/∂n= 0。流体中的总声压为壳体辐射直达声波与界面反射声波的叠加：

式中，

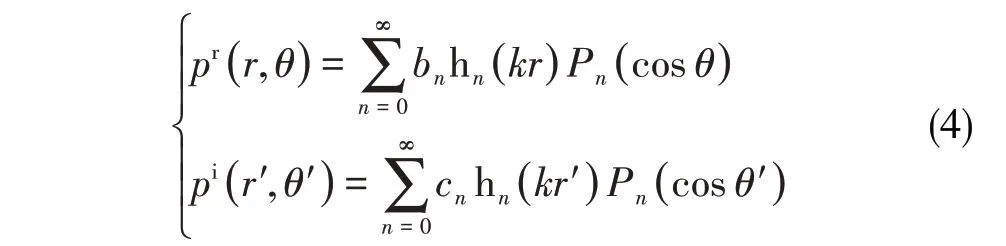
其中，k=ω/c，ω为角频率，c为流体中声速，bn,cn为未知展开系数，hn(kr)为n阶球Hankel函数；pr为辐射直达波，pi为界面反射波，(r,θ)和(r',θ' )分别为在实源O和虚源O'坐标系中的场点，如图1所示。

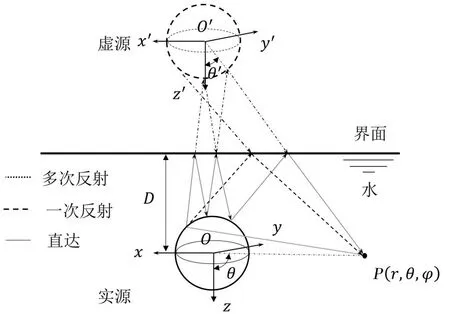
图1 界面附近球壳坐标示意图Fig.1 Schematic of a spherical shell submerged near the boundary

在界面上，r=r'，θ'=π-θ。当界面是软边界时，p=0，当界面是硬边界时，∂p/∂r= 0。可导出cn与bn的关系，统一表示为cn=V( -1)nbn，当界面为软边界时V=-1，硬边界时V=1。将式（4）的第二式中的下标n替换为q，利用Graf加法定理[12]得到总声压为

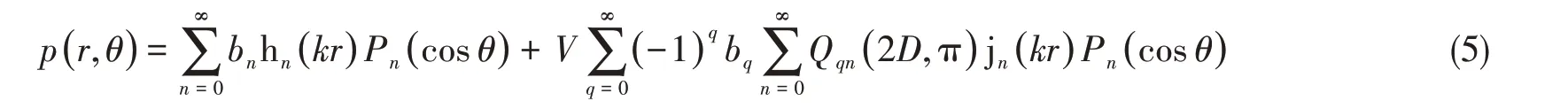
式中，D为壳体中心到界面的距离，jn( · )为n阶第一类球Bessel函数，且

上式中第一项即为壳体辐射直达声波的贡献，第二项表示界面反射声波的贡献。

利用壳体表面的振速连续条件

得到壳体第n阶径向振速为

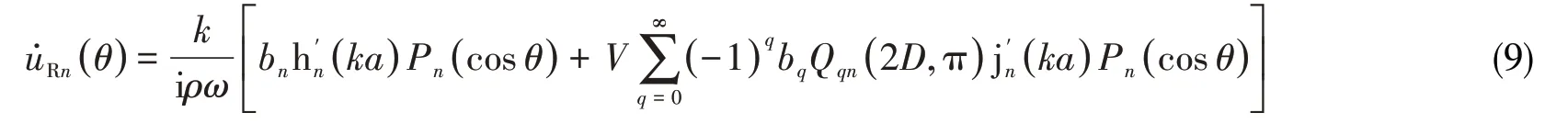
将式（2）、（7）和（9）代入式（1）中并将无穷级数项n截断为N项，得到声压展开系数满足的方程：

球壳的辐射声功率由表面振速和声压对其表面积分得到

式中，上标*表示取共轭。声功率级为20 lg(W/W0)，其中W0= 0.67×10-18W。

2 方法验证

考虑自由液面附近的外半径为a=1 m，厚度为hs=0.01 m，密度为ρs=7670 kg·m-3的钢球壳，杨氏模型为Es=1.85×1011Pa，泊松比为σs=0.3。外部为水，密度为ρf=1000 kg·m-3，声速为cf=1500 m·s-1，激励力位于球壳内壁（0,0,a-hs）点处（即θ0= 0），幅值为1 N。频率用无因次频率ka表示，球壳的下潜深度用无因次深度Hr=D/a表示。本文讨论球壳完全浸没在声学半空间中的情形，故归一化下潜深度的范围为Hr≥1。

利用Comsol有限元结果对本文方法的正确性进行验证。有限元模型中弹性球壳和水域分别采用固体力学模块和压力声学模块建模，声场域的无限远辐射条件采用完美匹配层（PML）模拟。图2（a）所示为球壳表点（0,0,a）处的径向振速，图2（b）所示为辐射声功率，球心与自由液面的归一化距离为Hr=2。可见解析结果与有限元结果吻合很好，验证了本文方法的正确性。

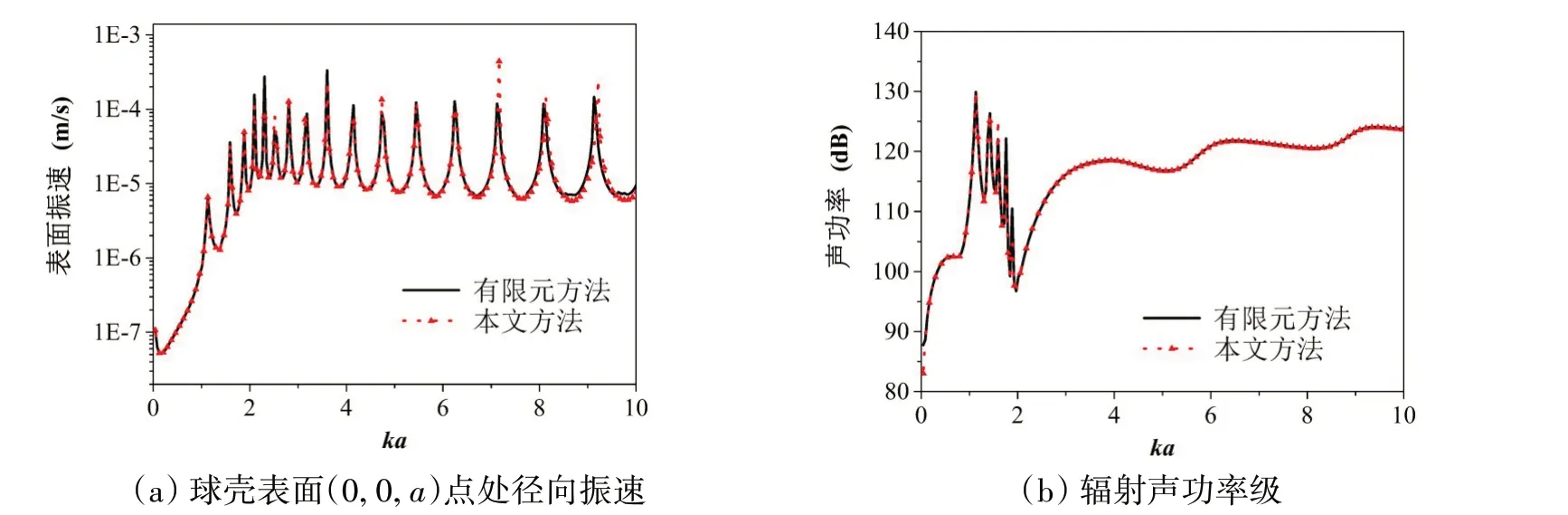
图2 本文方法和有限元方法的计算结果Fig.2 Calculation results by the method of this paper and FEM

3 界面对球壳声辐射的影响

界面对球壳声辐射的影响包含两方面：（1）声压场发生改变：界面的反射作用导致远场接收点处的声压为辐射直达波与界面反射波的相干叠加，导致声压频谱中呈现一系列干涉条纹；（2）声源特性发生改变：界面反射作用导致壳体的声辐射阻抗发生变化，从而改变壳体表面振动状态及辐射声压，进而引起球壳辐射声功率的变化，本文以声功率表示球壳的声源特性。以下计算中均将声压归一化到1 m处。

3.1 界面对辐射声场的影响

首先讨论辐射声阻抗的变化规律。分别将式（7）和式（9）写成矩阵形式：

得到模态声压与模态振速之间的关系式为

式中，

式中，第一项rnq为声辐射阻，表示表面声压与表面振速的相位相同，代表了向外辐射能量的大小；第二项mnq为声辐射抗，表示表面声压与表面振速相位差90°，因此这一项没有能量向外辐射，代表声场的惯性作用，又称为附加质量[20]。图3和图4分别给出了界面为软边界和硬边界时在给定无因次频率下（ka=1,2,5）模态比声辐射阻|rnq/rn|和比声辐射抗|mnq/mn|随下潜深度Hr的变化规律，其中Hr=1～10，rn和mn分别为球壳在自由场中的第n阶声辐射阻和声辐射抗。

对比图3和图4可见，比自辐射阻抗随着下潜深度的增加而逐渐趋于1，比互辐射阻抗则随着下潜深度的增加而逐渐趋于0；随着激励频率增加，声辐射阻抗的波动增强而幅值相应减小。因此，界面对声辐射阻抗的影响随频率和下潜深度的增加而逐渐减小。

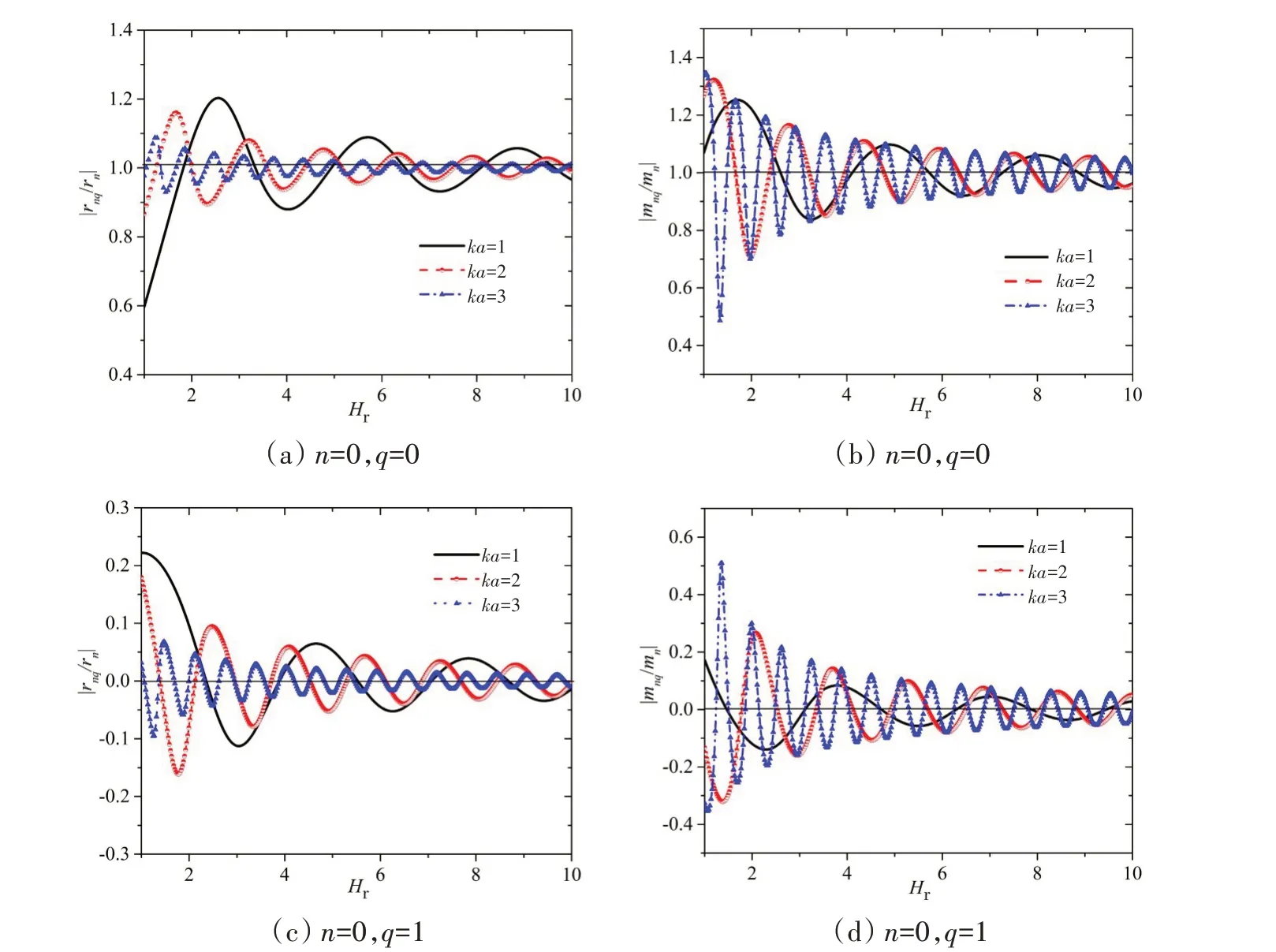
图3 软边界下球壳的模态比声辐射阻|rnq/rn|和比声辐射抗|mnq/mn|Fig.3 Relative acoustic radiation resistance|rnq/rn|and reactance|mnq/mn|of the spherical shell near the soft boundary

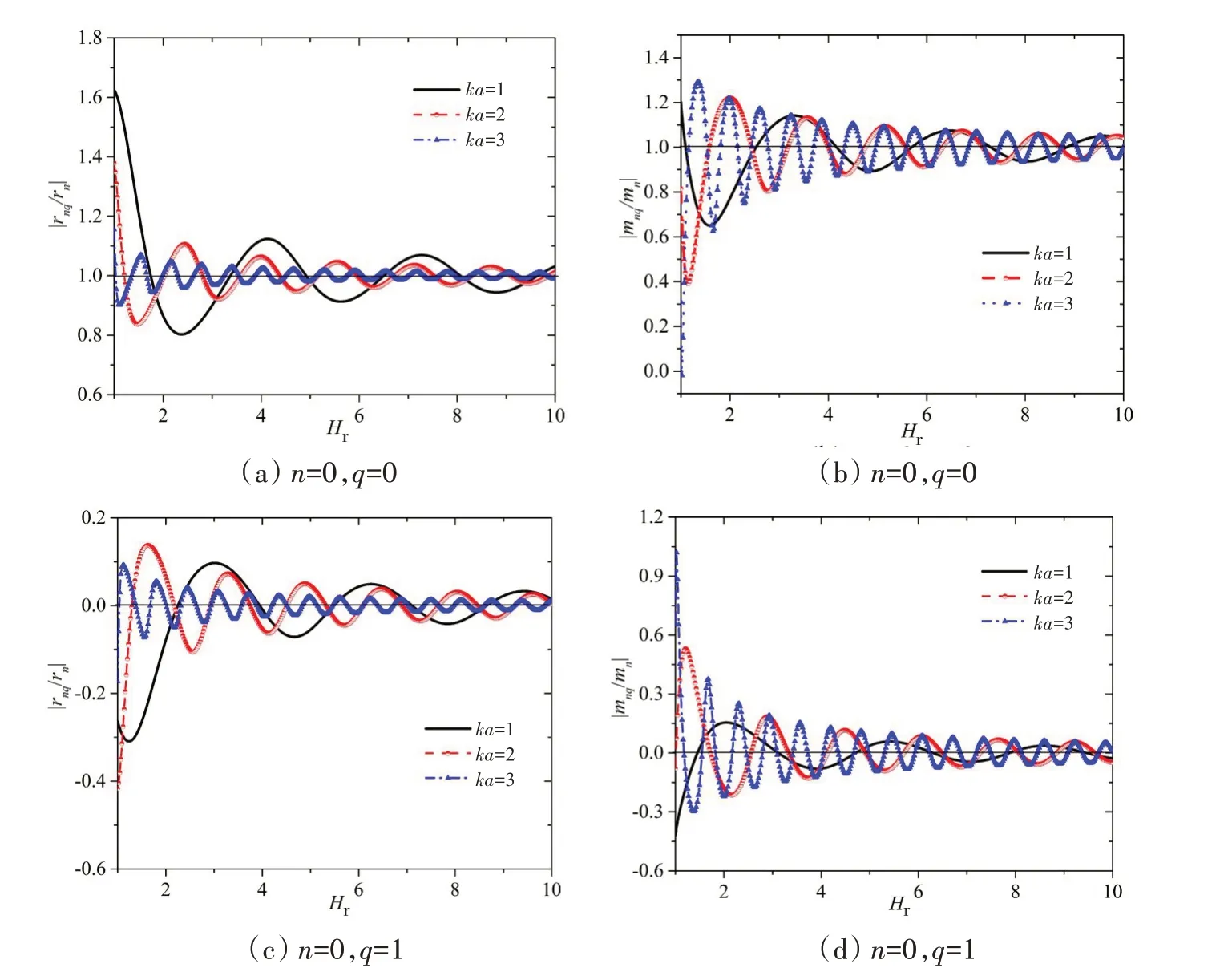
图4 硬边界下球壳的模态比声辐射阻|rnq/rn|和比声辐射抗|mnq/mn|Fig.4 Relative acoustic radiation resistance|rnq/rn|and reactance|mnq/mn|of the spherical shell near the hard boundary

互阻抗Zanq由界面与壳体间的多次散射作用产生，通过计算考虑和忽略互阻抗后的辐射声压，可以得到多次散射作用对球壳辐射声压的影响规律。图5给出了不同界面类型下壳体下潜深度分别为Hr=1、2、3 时考虑和忽略互阻抗Zanq时的声压随频率的变化结果，激励点位于θ0= 0。当球壳十分靠近界面（例如Hr=1）时，界面作用不仅影响声压幅值，而且会改变共振峰位置，这主要是界面与壳体之间的多次散射的贡献。对比不同潜深的结果可知：界面为软边界时，结构与界面之间的多次散射（互阻抗）对声压的贡献比硬边界时更大；随着壳体远离界面，忽略与考虑互阻抗的声压幅值差别减小（尤其是声压共振峰位置的差别明显减小），当壳体下潜深度Hr=3 时，忽略与考虑互阻抗时的声压幅值的差别已很小（最大差值为0.39 Pa）。因此，界面与壳体之间的多次散射作用随下潜深度增加而逐渐减弱。

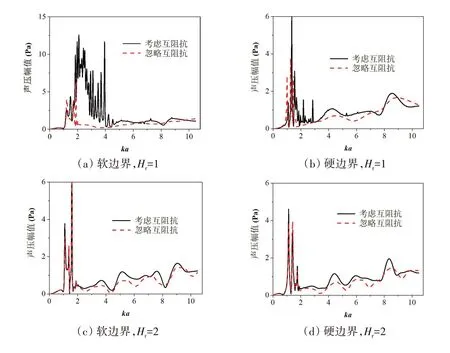
图5 忽略和考虑互阻抗时的声压幅值Fig.5 Sound pressure amplitude with considering and ignoring the mutual impedance

为更加直观地显示不同类型边界对球壳声辐射的影响，图6 分别给出软边界和硬边界附近球壳辐射声压的频率—深度谱，横坐标为无因次频率ka，纵坐标为归一化下潜深度Hr，用颜色代表声压幅值（Pa）。可见声压谱中出现两种类型的条纹：一种是随下潜深度基本不变的竖条纹，由壳体共振产生；另一种是与下潜深度和频率有关的明-暗相间的干涉条纹，这些条纹由辐射直达波与界面反射波之间的干涉形成。此外，干涉作用导致壳体辐射声压的共振峰出现明-暗相间的干涉条纹，而共振峰位置并不随下潜深度发生明显变化，这说明当壳体下潜深度较大时界面反射作用对壳体表面振动的影响较弱，可以忽略。

图6 界面附近弹性球壳辐射声压干涉亮条纹的预报结果Fig.6 Predicted interference fringe of the sound pressure radiated from the spherical shell submerged near the boundary

3.2 界面附近弹性球壳声辐射机理解释

忽略界面与球壳之间的多次散射作用时，球壳的辐射声场可近似为球壳辐射波与界面一次反射波的叠加场。设接收点位于( )r,θ处，以球心为等效声中心，得到直达波与反射波之间的声程差为2Dcosθ，则软边界反射引起声波干涉的频率变化可分别表示为

同样，硬边界反射引起的干涉条纹预报公式为

式（17）和式（18）预报结果在图6 中用红色虚线标出，为清晰起见，图中只给出前10 阶亮条纹位置，界面为软、硬边界时的亮条纹预报结果如图6 所示。可见预报结果与壳体共振峰中亮斑的中间位置及干涉条纹位置吻合很好。对比可知：（1）软边界和硬边界所形成干涉亮条纹的条件不同，经过软边界反射的声波相位变化π，形成的声场干涉条纹中有n=0 阶的干涉条纹，而硬边界导致的声场干涉条纹最低阶为n=1 阶；（2）两种类型的边界时，球壳的共振峰均因虚源干涉而形成明-暗相间的干涉条纹。

3.3 定量讨论界面对声源特性的影响

辐射声压不仅与球壳特性及激励频率有关，而且是空间坐标的函数，而声功率是声强对空间积分的结果，能够综合评价界面对球壳声源特性的影响。为确定界面对球壳声源特性的影响可以忽略的条件，取界面引起球壳声功率的变化量

来讨论界面的影响，其中W0为自由场中的声功率。

图7 所示为软边界和硬边界时的声功率差值ΔW随无因次频率ka及归一化下潜深度Hr的等高线图，图中只画出ΔW≥3 dB 的等高线区域，用颜色表示差值ΔW的大小，单位为dB。从图7 可知软边界对壳体声功率的影响比硬边界时更大，声功率差值大于3 dB 的区域集中在低频（ka＜2）和壳体靠近界面（Hr＜3）的范围内，其他区域均小于3 dB或无影响。

图7 界面附近弹性球壳声功率差值（壳厚hs/a=1%，激励力位于θ0 = 0）Fig.7 Difference of sound power with hs/a=1%,θ0 = 0

此外，激励位置和壳体厚度均会影响壳体的辐射声场，进一步给出激励力位于θ0= π 处、厚度半径比分别为1%及5%的结果，分别如图8 和图9 所示，其中图8（a）和图9（a）对应软边界，图8（b）和图9（b）对应硬边界。激励力位置不同导致球壳辐射声场指向性不同，当激励点位于靠近界面一侧（θ0=π）时，辐射声场主瓣指向界面，导致辐射声场受到界面影响比激励点位于远离界面一侧时更大，因此，图8中（θ0=π）的界面影响区域比图7中（θ0=0）更大。壳体厚度决定其弯曲刚度，当厚度增加后弯曲刚度也增大，导致球壳的辐射声场受到界面影响更小，因此图9中的界面影响区域比图8中更小。

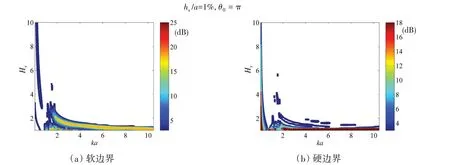
图8 界面附近弹性球壳声功率差值（壳厚hs/a=1%，激励力位于θ0 = π）Fig.8 Difference of sound power with hs/a=1%,θ0 = π

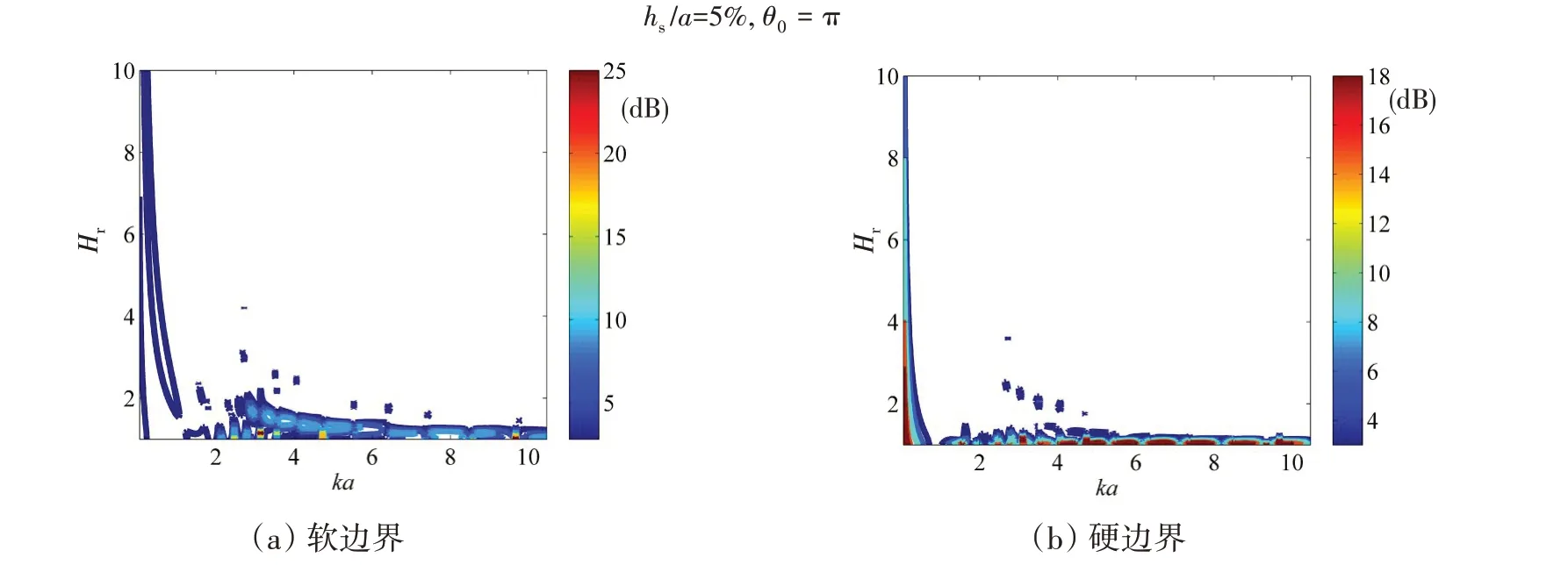
图9 界面附近弹性球壳声功率差值（壳厚hs/a=5%，激励力θ0 = π）Fig.9 Difference of sound power with hs/a=5%,θ0 = π

从上述几种情况的结果可见，当归一化频率和深度满足ka≥2 和Hr≥3 时，球壳声功率的差值小于3 dB，界面对球壳声源特性的影响可以忽略。因此，满足上述条件时界面附近壳体的声源特性可以用其自由场中的声源特性近似。

4 结 论

本文以界面附近的弹性球壳受内壁简谐点力激励的振动和声辐射为具体对象，利用Graf 加法定理和虚源法导出界面附近弹性球壳的振动和声辐射公式，解释了界面附近球壳辐射声场的形成机理，并讨论了界面对球壳辐射声阻抗、声压和声功率的影响规律，可以得到如下结论：

（1）界面与球壳之间的多次散射作用产生声辐射互阻抗，其随下潜深度和激励频率的增加而趋于零，故当球壳不十分靠近界面时（Hr≥3），多次散射作用可以忽略；

（2）界面附近球壳辐射声场的形成机理可以解释为共振和干涉，辐射声压的共振峰随下潜深度呈现为明-暗相间的干涉条纹，但共振峰位置并无明显变化；

（3）对于界面附近的薄球壳，在本文所讨论的壳厚（h/a=1%～5%）范围内，当无因次频率ka≥2且归一化下潜深度Hr≥3时，界面对球壳辐射声功率的影响小于3 dB，可以忽略。